勾股定理
图片预览




文档简介
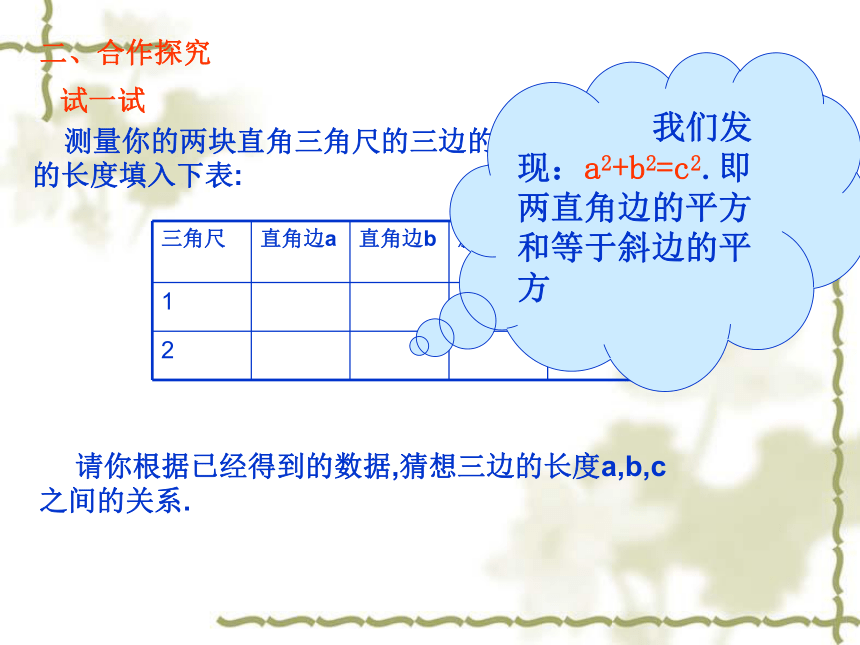
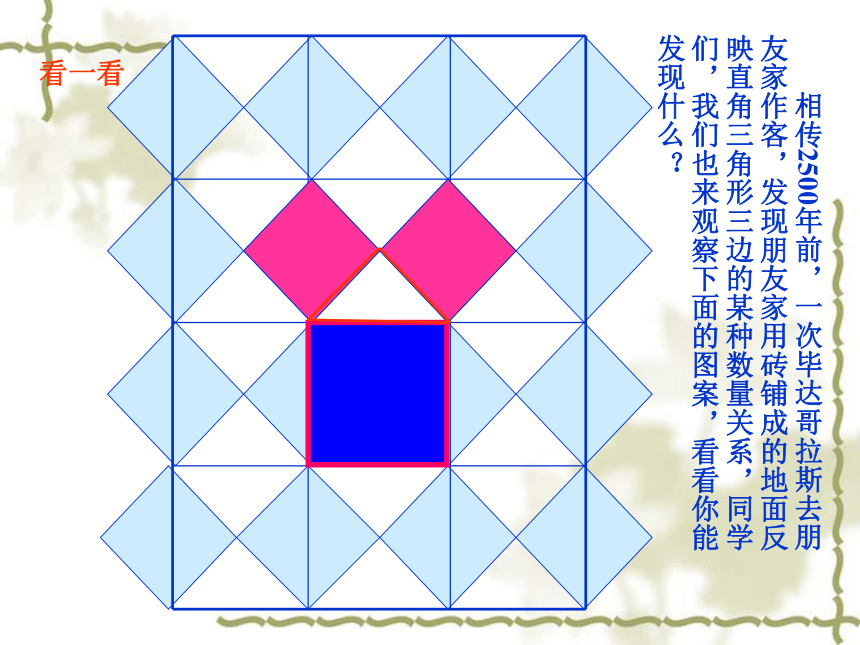
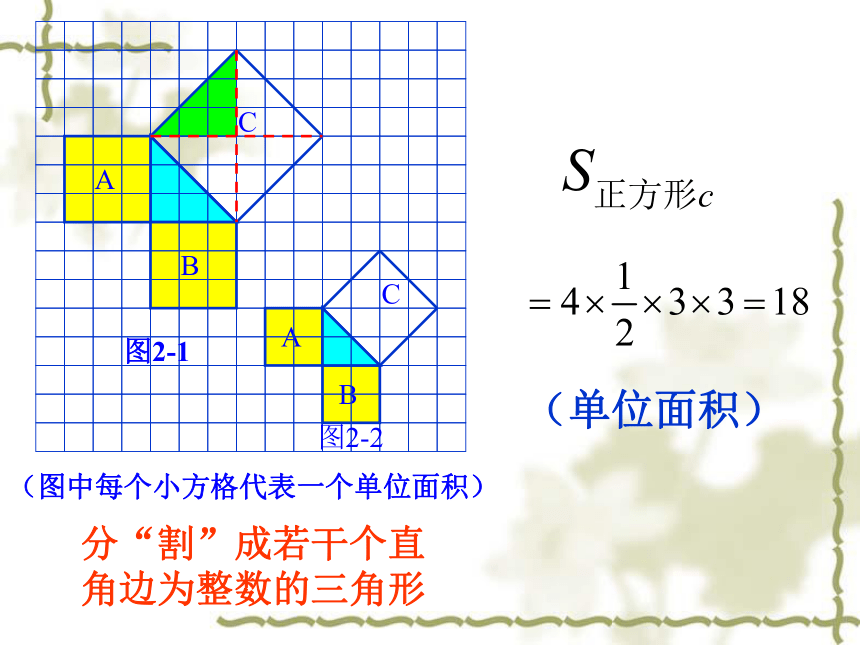
课件24张PPT。勾股定理2002年国际数学家大会在北京召开一、情景引入试一试 测量你的两块直角三角尺的三边的长度,并将各边的长度填入下表: 请你根据已经得到的数据,猜想三边的长度a,b,c之间的关系. 我们发现:a2+b2=c2.即两直角边的平方和等于斜边的平方二、合作探究 相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?看一看(1)观察图2-1
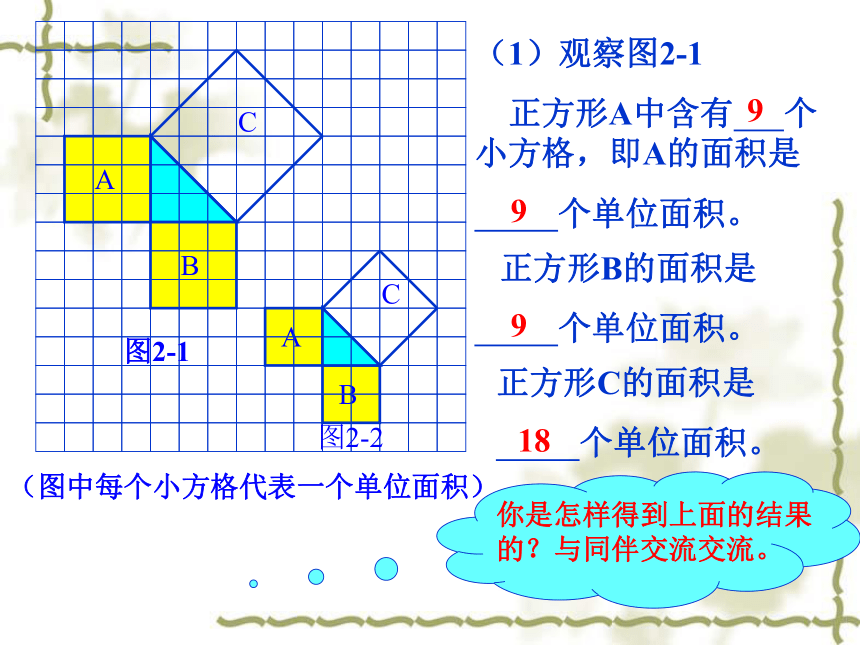
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。99918你是怎样得到上面的结果的?与同伴交流交流。分“割”成若干个直角边为整数的三角形(单位面积)(单位面积)把C“补” 成边长为6的正方形面积的一半分割成若干个直角边为整数的三角形(面积单位)一般的直角三角形三边为边作正方形做一做 在图的方格中,用三角尺画出两条直角边分别5cm、12cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立.52+122=( )213勾股定理(毕达哥拉斯定理)(gou-gu theorem) 如果直角三角形两直角边分别为a, b,斜边为c,那么 即直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股BCA1.在Rt△ABC中,∠A,∠B,∠C的对边
为a,b,c
(1)已知a=6,b=8.则c= .
练习1102012(2)已知c=25,b=15.则a= .(3)已知c=19,a=13.则b= .
(结果保留根号)
(4)已知a:b=3:4,c=15,则b= .三、巩固练习. 如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?可要当心噢!练习2(分类讨论的数学思想)1、如图所示,一块长3m,宽2.2m的薄木板能否从城门内通过?为什么?2mDCAB 1m四、生活运用答:大树在折断之前高为36米。
26+10 = 36(米)解:利用勾股定理可以求折断倒下部分的长度为:2、受大风和雷电影响,一棵树在离地面10米处断裂,树的顶部落在离树跟底部24米处,这棵树折断前有多高?
3、 有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解:设水深为X尺,则芦苇长为(X+1)尺,由勾股定理得
(X+1)2=X2+(102)2
解得 X=12
∴X+1=13 (X+1)2=X2+(102)2
解得 X=12
∴X+1=13答:水池的深度为12尺,芦苇长为13尺。解得 X=124、 如图:一块长约80 m、宽约60 m的长方形草坪,被几个不自觉的学生沿对角线踏出了一条斜“路”,这种情况在生活中时有发生。请问同学们:
(1)这几位同学为什么不走正路,走斜“路”? (2)他们知道走斜“路”比正路少走几步吗?
(3)他们这样这样做,值得吗?
80m60m 如图,有一个圆柱体,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B处的食物,需要爬行的最短路程是多少?(π的值取3)蛋糕B拓展延伸:.BB12OA3蛋糕AC五、课堂小结: 你这节课的主要收获是什么?本节课到此结束,
谢谢大家!? ?在古汉语里,人们将手臂弯曲成直角,上半部分称为“勾”,下半部分称为“股”.
在直角三角形中,一般的,我们把较短的直角边叫做“勾”,较长的直角边叫做“股”,斜边叫做“弦”.???
你知道“勾股定理” 的字义吗?
何谓“勾、股”呢?
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。99918你是怎样得到上面的结果的?与同伴交流交流。分“割”成若干个直角边为整数的三角形(单位面积)(单位面积)把C“补” 成边长为6的正方形面积的一半分割成若干个直角边为整数的三角形(面积单位)一般的直角三角形三边为边作正方形做一做 在图的方格中,用三角尺画出两条直角边分别5cm、12cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立.52+122=( )213勾股定理(毕达哥拉斯定理)(gou-gu theorem) 如果直角三角形两直角边分别为a, b,斜边为c,那么 即直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股BCA1.在Rt△ABC中,∠A,∠B,∠C的对边
为a,b,c
(1)已知a=6,b=8.则c= .
练习1102012(2)已知c=25,b=15.则a= .(3)已知c=19,a=13.则b= .
(结果保留根号)
(4)已知a:b=3:4,c=15,则b= .三、巩固练习. 如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?可要当心噢!练习2(分类讨论的数学思想)1、如图所示,一块长3m,宽2.2m的薄木板能否从城门内通过?为什么?2mDCAB 1m四、生活运用答:大树在折断之前高为36米。
26+10 = 36(米)解:利用勾股定理可以求折断倒下部分的长度为:2、受大风和雷电影响,一棵树在离地面10米处断裂,树的顶部落在离树跟底部24米处,这棵树折断前有多高?
3、 有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解:设水深为X尺,则芦苇长为(X+1)尺,由勾股定理得
(X+1)2=X2+(102)2
解得 X=12
∴X+1=13 (X+1)2=X2+(102)2
解得 X=12
∴X+1=13答:水池的深度为12尺,芦苇长为13尺。解得 X=124、 如图:一块长约80 m、宽约60 m的长方形草坪,被几个不自觉的学生沿对角线踏出了一条斜“路”,这种情况在生活中时有发生。请问同学们:
(1)这几位同学为什么不走正路,走斜“路”? (2)他们知道走斜“路”比正路少走几步吗?
(3)他们这样这样做,值得吗?
80m60m 如图,有一个圆柱体,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B处的食物,需要爬行的最短路程是多少?(π的值取3)蛋糕B拓展延伸:.BB12OA3蛋糕AC五、课堂小结: 你这节课的主要收获是什么?本节课到此结束,
谢谢大家!? ?在古汉语里,人们将手臂弯曲成直角,上半部分称为“勾”,下半部分称为“股”.
在直角三角形中,一般的,我们把较短的直角边叫做“勾”,较长的直角边叫做“股”,斜边叫做“弦”.???
你知道“勾股定理” 的字义吗?
何谓“勾、股”呢?
