9.1.1不等式及其解集课件
文档属性
| 名称 | 9.1.1不等式及其解集课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 259.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-14 20:50:59 | ||
图片预览











文档简介
课件38张PPT。 第九章 不等式与不等式组
1.不等式
2.一元一次不等式
3.一元一次不等式组9.1.1 不等式及其解集数量有大小之分,它们之间有相等关系,
也有不等关系,
日常生活中存在大量涉及不等关系的问题,
例,当两家商场推出不同的优惠方案时,
到哪家商场购物花费少?
这个问题就蕴含了不等关系,
对于这样的问题,我们常分析其中的不等关系,
列车相应的数学式子——不等式(组)
并通过解不等式(组)而得出结论,
这样的思路与利用方程研究相等关系是类似的。不等式的性质一元一次不等式一元一次不等式组不等式本章学习内容不等式的解不等式的解集不等式解集的表示方法不等式本节学习内容你还记得小孩玩的翘翘板吗?
你想过它的工作原理吗?看一看在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
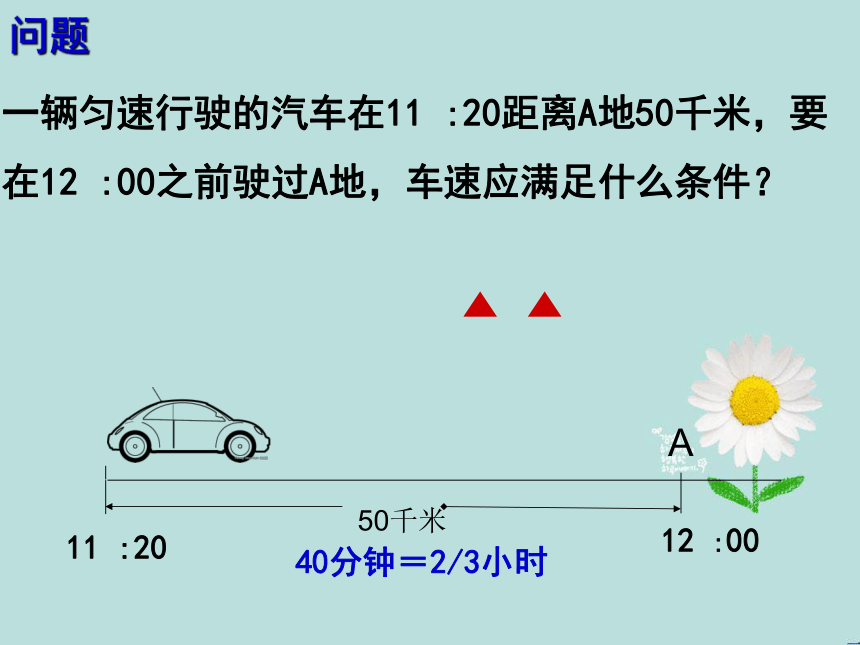
并把它们用到了生活实践当中.不相等 处处可见不等式一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前驶过A地,车速应满足什么条件?A50千米问题11 :2012 :0040分钟=2/3小时设车速是x千米/时从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50千米所用的时间不到2/3小时,即
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶2/3小时的路程要超过50千米,即
①②分析:一.不等式①②用“>”或“<”表示大小关系的式子,叫做不等式.不等式中常见的不等号有五种: “>”、“<”、 “≥”、“≤” 、“≠”有些不等式中不含未知数,
例如: 3<4,-1>-2.
有些不等式中含有未知数,
例①和②中用x表示未知数。注意:
(1)像a≥b或b≤a这样的式子,也经常用来表示两
个数量的大小关系。
(2)由不等式定义还可以知道,不等式可以分成两
大类:
①表示大小关系的不等式,符号类型有
>,<,≥,≤;
②表示不等关系的不等式,符号为≠,读不等于。例1 用不等式表示下列关系:
(1)m与3的和小于n;解:m+3<n;(2)x与12的差比y的3倍大;解: x-12>3y;(3)a与b的乘积是正数;解: ab>0;(5)x与y的和的不小于-2;解:x+y ≥ -2;(6)a与b的和的20%至多为15.解: x-12>3y;(4)x与12的差比y的3倍大;解:20%(a+b) ≤151.下列式子哪些是不等式?哪些不是不等式?
-2<5
x+3>6
4x-2y≤0
a-2ba+b≠c
5m+3=8
8+4<7
火眼金睛答:①②③⑤⑦⑧是不等式,④⑥不是,
因为④不含不等号,⑥是等式。2.用不等式表示下列语句。
①a的相反数是正数;
②y的一半与x的2倍的和小于3;
③x与3的差的2倍小于x与4的和;
④a的 与b的4倍的和是负数。
思考: 问题1:要使汽车在12:00以前驶过A地,你认为车 速应该是多少呢?问题2:对于不等式 ,
当x=80时,
当x=78时,
当x=75时,
当x=72时,x=50x<50这就是说,当x取某些值时,不等式 成立;
当x取某些值时,不等式 不成立。
与方程的解类似,我们把使不等式成立的未知数的值叫做不等式的解。
例 80和78是不等式 的解,而75和72不是
不等式 的解。代入法是检验某个值是否是不等式的解的简单、实用的方法;解:当x=75时, ,
不等式不成立,
所以x=75不是不等式 的解;思考x=78是不等式 的解吗?练习:
下列数中哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 8,
2.5, 3, 3.2, 4.8, 12思考: 对于不等式 ,
当x=80时,
当x=78时,
当x=75时,
当x=72时,x=50x<50除了80和78,不等式
还有其他的解吗?
如果有,这些解应满足
什么条件?可以发现,当x>75时,不等式 总成立;
当x<75时,不等式 不成立。
这就是说,任何一个大于75的数都是不等式的解,
这样的解有无数个;
任何一个小于或等于75的数不是不等式
的解。
因此,x>75表示了能使不等式 成立的取值范围,它可以在数轴上表示。
所以,在前面问题中,汽车要在12:00之前驶过A地,
车速必须大于75km/h.一般地,一个含有未知数的不等式的所有的解组成这个不等式的解集。
求不等式的解集的过程叫解不等式。想一想:
1.不等式的解和不等式的解集是一样的吗?
解:单独使不等式成立的一个数只是不等式一个解。
解集:不等式的解集是一个集合,所有解的集合;
2.不等式的解与解不等式一样吗?不等式的解集在数轴上表示,分三步进行:
①画数轴 ②定界点 ③定方向表示不包括这一点
表示包括这一点大于小于向右画
向左画1.用数轴表示不等式的解集的步骤:
①画数轴; ②定界点; ③定方向.
2.用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
有等号(≥ ,≤)画实心点,无等号(>,<)画空心圆. 解集的表示方法:第一种:用式子,x>a或x 如不等式 的解集可以用不等式
x >75来表示。第二种:用数轴,
标出数轴上某一区间,其中的点对应的数
值都是不等式的解.
直接想出不等式的解集:
⑴ x+2>6 ⑵ 3x>9 ⑶ x-3>0解: ⑴ x>4 ; ⑵ x>3 ; ⑶ x>3.尝试练习 练习:
1.一般地,一个含有未知数的不等式的______的解,
叫做这个不等式的解集。
2.求不等式的______的过程叫做解不等式。
3.不等式的解集在数轴上表示,分三步进行:
①_________; ②_________;③__________.
4.如图所示的不等式的解集,与其对应的不等式应
是_______. 5.利用数轴表示下面未知数的取值范围。
(1)x≥-3 (2)x≤-1 (3)x<
6.在数轴上表示不等式x-3<0的解集_________.
7.不等式x+2>6的解集为_________.
8.想一想:
1.不等式的解和不等式的解集是一样的吗?
解:单独使不等式成立的一个数只是不等式一个解。
解集:不等式的解集是一个集合,所有解的集合;
2.不等式的解与解不等式一样吗? 练习:
1.下列说法正确的是( )
A.x=5是不等式4x>25的解
B.x=2是不等式-x<2的解集
C.x>-3是不等式2x>-1的解集
D.不等式x+2<4的解集是x<2
2.下列说法正确的是( )
A. x=3是2x+1>5的解
B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解
D. x=3是2x+1>5的解集
3.下列说法正确吗?为什么?
①不等式x<2有一个正整数解;
②不等式x-1<0的解集是x<-1;
③不等式x<10的整数解有无数个。
4.x<2的非负整数解的个数有( )
A.3个 B.2个 C.1个 D.无数个
5.求不等式2x<5的正整数解。
6.关于x的一元一次方程 = 的解是负数
求a的取值范围。
7.无论x为何值,下列不等式总成立的是( )
A.(x+3)2>0 B.(x+3)2<0
C.(x+3)2>0或(x+3)2=0 D.(x+3)2≠0
8.①0”连接下列各式:
x2 x
②当ab<0时,用“<”连接下列各式:
(a+b)2 、 (a-b)2、 a2+b228.若x+y<0,xy<0,x 是______.
9.某市自来水公司收费标准如下:每户每月用水不超过6m3,收费1.5元/m3;若超过6m3,则超过的部分按2元/m3收费。小超家某月水费不足12元,若设小超家该月的用水量为xm3.
(1)x应满足什么关系式?
(2)小超家该月的用水量有可能是6m3或8m3吗?
10.小刚准备各用自己节省的零花钱买一部MP4来学
习英语,他已存有50元并计划以后每月再存30
元,直到他存的钱超过220元才可以买。设x个
月后小刚的钱超过220元,请你列出不等式,并
找出满足此不等式的最小整数。
1.不等式
2.一元一次不等式
3.一元一次不等式组9.1.1 不等式及其解集数量有大小之分,它们之间有相等关系,
也有不等关系,
日常生活中存在大量涉及不等关系的问题,
例,当两家商场推出不同的优惠方案时,
到哪家商场购物花费少?
这个问题就蕴含了不等关系,
对于这样的问题,我们常分析其中的不等关系,
列车相应的数学式子——不等式(组)
并通过解不等式(组)而得出结论,
这样的思路与利用方程研究相等关系是类似的。不等式的性质一元一次不等式一元一次不等式组不等式本章学习内容不等式的解不等式的解集不等式解集的表示方法不等式本节学习内容你还记得小孩玩的翘翘板吗?
你想过它的工作原理吗?看一看在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.不相等 处处可见不等式一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前驶过A地,车速应满足什么条件?A50千米问题11 :2012 :0040分钟=2/3小时设车速是x千米/时从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50千米所用的时间不到2/3小时,即
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶2/3小时的路程要超过50千米,即
①②分析:一.不等式①②用“>”或“<”表示大小关系的式子,叫做不等式.不等式中常见的不等号有五种: “>”、“<”、 “≥”、“≤” 、“≠”有些不等式中不含未知数,
例如: 3<4,-1>-2.
有些不等式中含有未知数,
例①和②中用x表示未知数。注意:
(1)像a≥b或b≤a这样的式子,也经常用来表示两
个数量的大小关系。
(2)由不等式定义还可以知道,不等式可以分成两
大类:
①表示大小关系的不等式,符号类型有
>,<,≥,≤;
②表示不等关系的不等式,符号为≠,读不等于。例1 用不等式表示下列关系:
(1)m与3的和小于n;解:m+3<n;(2)x与12的差比y的3倍大;解: x-12>3y;(3)a与b的乘积是正数;解: ab>0;(5)x与y的和的不小于-2;解:x+y ≥ -2;(6)a与b的和的20%至多为15.解: x-12>3y;(4)x与12的差比y的3倍大;解:20%(a+b) ≤151.下列式子哪些是不等式?哪些不是不等式?
-2<5
x+3>6
4x-2y≤0
a-2ba+b≠c
5m+3=8
8+4<7
火眼金睛答:①②③⑤⑦⑧是不等式,④⑥不是,
因为④不含不等号,⑥是等式。2.用不等式表示下列语句。
①a的相反数是正数;
②y的一半与x的2倍的和小于3;
③x与3的差的2倍小于x与4的和;
④a的 与b的4倍的和是负数。
思考: 问题1:要使汽车在12:00以前驶过A地,你认为车 速应该是多少呢?问题2:对于不等式 ,
当x=80时,
当x=78时,
当x=75时,
当x=72时,x=50x<50这就是说,当x取某些值时,不等式 成立;
当x取某些值时,不等式 不成立。
与方程的解类似,我们把使不等式成立的未知数的值叫做不等式的解。
例 80和78是不等式 的解,而75和72不是
不等式 的解。代入法是检验某个值是否是不等式的解的简单、实用的方法;解:当x=75时, ,
不等式不成立,
所以x=75不是不等式 的解;思考x=78是不等式 的解吗?练习:
下列数中哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 8,
2.5, 3, 3.2, 4.8, 12思考: 对于不等式 ,
当x=80时,
当x=78时,
当x=75时,
当x=72时,x=50x<50除了80和78,不等式
还有其他的解吗?
如果有,这些解应满足
什么条件?可以发现,当x>75时,不等式 总成立;
当x<75时,不等式 不成立。
这就是说,任何一个大于75的数都是不等式的解,
这样的解有无数个;
任何一个小于或等于75的数不是不等式
的解。
因此,x>75表示了能使不等式 成立的取值范围,它可以在数轴上表示。
所以,在前面问题中,汽车要在12:00之前驶过A地,
车速必须大于75km/h.一般地,一个含有未知数的不等式的所有的解组成这个不等式的解集。
求不等式的解集的过程叫解不等式。想一想:
1.不等式的解和不等式的解集是一样的吗?
解:单独使不等式成立的一个数只是不等式一个解。
解集:不等式的解集是一个集合,所有解的集合;
2.不等式的解与解不等式一样吗?不等式的解集在数轴上表示,分三步进行:
①画数轴 ②定界点 ③定方向表示不包括这一点
表示包括这一点大于小于向右画
向左画1.用数轴表示不等式的解集的步骤:
①画数轴; ②定界点; ③定方向.
2.用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
有等号(≥ ,≤)画实心点,无等号(>,<)画空心圆. 解集的表示方法:第一种:用式子,x>a或x
x >75来表示。第二种:用数轴,
标出数轴上某一区间,其中的点对应的数
值都是不等式的解.
直接想出不等式的解集:
⑴ x+2>6 ⑵ 3x>9 ⑶ x-3>0解: ⑴ x>4 ; ⑵ x>3 ; ⑶ x>3.尝试练习 练习:
1.一般地,一个含有未知数的不等式的______的解,
叫做这个不等式的解集。
2.求不等式的______的过程叫做解不等式。
3.不等式的解集在数轴上表示,分三步进行:
①_________; ②_________;③__________.
4.如图所示的不等式的解集,与其对应的不等式应
是_______. 5.利用数轴表示下面未知数的取值范围。
(1)x≥-3 (2)x≤-1 (3)x<
6.在数轴上表示不等式x-3<0的解集_________.
7.不等式x+2>6的解集为_________.
8.想一想:
1.不等式的解和不等式的解集是一样的吗?
解:单独使不等式成立的一个数只是不等式一个解。
解集:不等式的解集是一个集合,所有解的集合;
2.不等式的解与解不等式一样吗? 练习:
1.下列说法正确的是( )
A.x=5是不等式4x>25的解
B.x=2是不等式-x<2的解集
C.x>-3是不等式2x>-1的解集
D.不等式x+2<4的解集是x<2
2.下列说法正确的是( )
A. x=3是2x+1>5的解
B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解
D. x=3是2x+1>5的解集
3.下列说法正确吗?为什么?
①不等式x<2有一个正整数解;
②不等式x-1<0的解集是x<-1;
③不等式x<10的整数解有无数个。
4.x<2的非负整数解的个数有( )
A.3个 B.2个 C.1个 D.无数个
5.求不等式2x<5的正整数解。
6.关于x的一元一次方程 = 的解是负数
求a的取值范围。
7.无论x为何值,下列不等式总成立的是( )
A.(x+3)2>0 B.(x+3)2<0
C.(x+3)2>0或(x+3)2=0 D.(x+3)2≠0
8.①0
x2 x
②当ab<0时,用“<”连接下列各式:
(a+b)2 、 (a-b)2、 a2+b228.若x+y<0,xy<0,x
9.某市自来水公司收费标准如下:每户每月用水不超过6m3,收费1.5元/m3;若超过6m3,则超过的部分按2元/m3收费。小超家某月水费不足12元,若设小超家该月的用水量为xm3.
(1)x应满足什么关系式?
(2)小超家该月的用水量有可能是6m3或8m3吗?
10.小刚准备各用自己节省的零花钱买一部MP4来学
习英语,他已存有50元并计划以后每月再存30
元,直到他存的钱超过220元才可以买。设x个
月后小刚的钱超过220元,请你列出不等式,并
找出满足此不等式的最小整数。
