4.1数列的前n项和及斐波那契数列课件(共17张)-2023-2024学年高二上学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.1数列的前n项和及斐波那契数列课件(共17张)-2023-2024学年高二上学期数学人教A版(2019)选择性必修第二册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 16:51:28 | ||
图片预览






文档简介
(共17张PPT)
4.1 数列的前n项和及斐波那契数列
问题1:什么是数列的前n项和公式?
探索数列的求和公式,曾是古代算学家非常感兴趣的问题.
问题2:数列的前n项和公式与通项公式有何联系?
数列的前n项和
数列{an}从第1项a1到第n项an的各项之和,称为数列{an}的前n项和,记作Sn,即Sn =a1+a2+...+an
数列{an}的前n项和Sn与序号n之间的关系式叫做数列的前n项和公式.
Sn =a1+a2+...+an-1+an
Sn-1 =a1+a2+...+an-1(n≥2)
an=Sn-Sn-1 (n≥2)
P7-思考:已知数列{an}的前n项和公式为Sn =n2+n, 求数列{an}的通项公式.
[练习1]已知数列{an}的前n项和公式为Sn =﹣2n2+1, 求数列{an}的通项公式.
分段求解,
检验结果能否统一形式
阅读与思考
斐波那契数列
1202年,意大利数学家斐波那契(Leonardo Fibonacci,约1170—约1250)出版了他的《算盘全书》(Liber Abaci).他在书中收录了一些有意思的问题,其中有一个关于兔子繁殖的问题:
如果1对兔子每月能生1对小兔子(一雄一雌),而每1对小兔子在它出生后的第3个月里,又能生1对小兔子,假定在不发生死亡的情况下,由1对初生的小兔子开始,50个月后会有多少对兔子?
斐波那契在《算盘书》中的兔子繁殖问题(兔子数单位:对)
如果1对兔子每月能生1对小兔子(一雄一雌),而每1对小兔子在它出生后的第3个月里,又能生1对小兔子,假定在不发生死亡的情况下,由1对初生的小兔子开始,50个月后会有多少对兔子
时间/月 初生兔子/对 成熟兔子/对 兔子总数/对
1 1 0 1
2 0 1 1
3 1 1 2
4 1 2 3
5 2 3 5
6 3 5 8
7 5 8 13
8 8 13 21
9 13 21 34
10 21 34 55
11 34 55 89
12 55 89 144
… … … …
由此可知,从第1个月开始,每月末的兔子总对数是
1,1,2,3,5,8,13,21,34,55,89,144,….
你发现这个数列的规律了吗?
黄金分割点
1
1
1
1
斐波那契数列有很多有趣的性质.
例如,斐波那契数列满足等式,
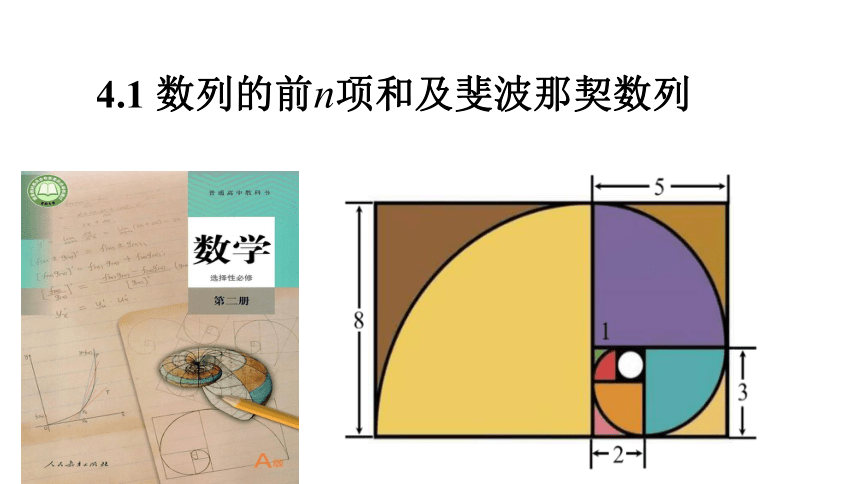
我们可以用图形(图1)来表示这个等式.
图1中小正方形的边长等于斐波那契数1,1,2,3,5,8,….
若干小正方形构成的长方形的边长依次是两个斐波那契数的乘积,,,….
如图1所示,从内到外依次连接通过小正方形的四分之一圆弧,
就得到了一条被称为“斐波那契螺旋”的弧线.
如果我们在图1
上不断增加边长是斐波那契数的正方形,
那么“斐波那契螺旋”也将不断向外延伸,
而且它的形状将越来越接近“黄金比例螺旋”.
绘制斐波那契螺旋线,验证课本P11的结论
{an}: 1,1, 2, 3, 5, 8, 13, 21, 34, 55,…
+…+
随着边长的增加,螺旋线的形状越来越接近“黄金比例螺旋”.
前n个小正方形的面积和为相邻两个斐波那契数an与an+1之积
(n≥2)
向日葵花盘上的螺旋线条,
顺时针的螺旋线:21条;
逆时针的螺旋线:34条。
松果上的螺旋线条,
顺时针的螺旋线:8条;
逆时针的螺旋线:13条。
更加有趣的是,人们在自然界中发现了许多斐波那契数列.
例如,一棵树在第一年长出一条新枝,新枝成长一年后变为老枝,老枝每年都长出一条新枝.每一条树枝都按照这个规律成长,则每年的树枝总数正好构成了斐波那契数列.又如,图2中向日葵的管状小花排列成两组交错的螺旋,从内往外看,逆时针方向的螺旋有13条,
顺时针方向的有21条,
恰为斐波那契数列的相邻两项.
蒲公英的种子和松塔的鳞片的排列
也呈现出类似的规律.
由于斐波那契数列的广泛应用性,美国成立了斐波那契协会,并于1963年创办《斐波那契季刊》,专门发表关于这个数列的研究论文.
有兴趣的同学可以通过浏览互联网或查阅相关书籍搜集资料,进一步了解盘研究斐波那契数列.
4.1 数列的前n项和及斐波那契数列
问题1:什么是数列的前n项和公式?
探索数列的求和公式,曾是古代算学家非常感兴趣的问题.
问题2:数列的前n项和公式与通项公式有何联系?
数列的前n项和
数列{an}从第1项a1到第n项an的各项之和,称为数列{an}的前n项和,记作Sn,即Sn =a1+a2+...+an
数列{an}的前n项和Sn与序号n之间的关系式叫做数列的前n项和公式.
Sn =a1+a2+...+an-1+an
Sn-1 =a1+a2+...+an-1(n≥2)
an=Sn-Sn-1 (n≥2)
P7-思考:已知数列{an}的前n项和公式为Sn =n2+n, 求数列{an}的通项公式.
[练习1]已知数列{an}的前n项和公式为Sn =﹣2n2+1, 求数列{an}的通项公式.
分段求解,
检验结果能否统一形式
阅读与思考
斐波那契数列
1202年,意大利数学家斐波那契(Leonardo Fibonacci,约1170—约1250)出版了他的《算盘全书》(Liber Abaci).他在书中收录了一些有意思的问题,其中有一个关于兔子繁殖的问题:
如果1对兔子每月能生1对小兔子(一雄一雌),而每1对小兔子在它出生后的第3个月里,又能生1对小兔子,假定在不发生死亡的情况下,由1对初生的小兔子开始,50个月后会有多少对兔子?
斐波那契在《算盘书》中的兔子繁殖问题(兔子数单位:对)
如果1对兔子每月能生1对小兔子(一雄一雌),而每1对小兔子在它出生后的第3个月里,又能生1对小兔子,假定在不发生死亡的情况下,由1对初生的小兔子开始,50个月后会有多少对兔子
时间/月 初生兔子/对 成熟兔子/对 兔子总数/对
1 1 0 1
2 0 1 1
3 1 1 2
4 1 2 3
5 2 3 5
6 3 5 8
7 5 8 13
8 8 13 21
9 13 21 34
10 21 34 55
11 34 55 89
12 55 89 144
… … … …
由此可知,从第1个月开始,每月末的兔子总对数是
1,1,2,3,5,8,13,21,34,55,89,144,….
你发现这个数列的规律了吗?
黄金分割点
1
1
1
1
斐波那契数列有很多有趣的性质.
例如,斐波那契数列满足等式,
我们可以用图形(图1)来表示这个等式.
图1中小正方形的边长等于斐波那契数1,1,2,3,5,8,….
若干小正方形构成的长方形的边长依次是两个斐波那契数的乘积,,,….
如图1所示,从内到外依次连接通过小正方形的四分之一圆弧,
就得到了一条被称为“斐波那契螺旋”的弧线.
如果我们在图1
上不断增加边长是斐波那契数的正方形,
那么“斐波那契螺旋”也将不断向外延伸,
而且它的形状将越来越接近“黄金比例螺旋”.
绘制斐波那契螺旋线,验证课本P11的结论
{an}: 1,1, 2, 3, 5, 8, 13, 21, 34, 55,…
+…+
随着边长的增加,螺旋线的形状越来越接近“黄金比例螺旋”.
前n个小正方形的面积和为相邻两个斐波那契数an与an+1之积
(n≥2)
向日葵花盘上的螺旋线条,
顺时针的螺旋线:21条;
逆时针的螺旋线:34条。
松果上的螺旋线条,
顺时针的螺旋线:8条;
逆时针的螺旋线:13条。
更加有趣的是,人们在自然界中发现了许多斐波那契数列.
例如,一棵树在第一年长出一条新枝,新枝成长一年后变为老枝,老枝每年都长出一条新枝.每一条树枝都按照这个规律成长,则每年的树枝总数正好构成了斐波那契数列.又如,图2中向日葵的管状小花排列成两组交错的螺旋,从内往外看,逆时针方向的螺旋有13条,
顺时针方向的有21条,
恰为斐波那契数列的相邻两项.
蒲公英的种子和松塔的鳞片的排列
也呈现出类似的规律.
由于斐波那契数列的广泛应用性,美国成立了斐波那契协会,并于1963年创办《斐波那契季刊》,专门发表关于这个数列的研究论文.
有兴趣的同学可以通过浏览互联网或查阅相关书籍搜集资料,进一步了解盘研究斐波那契数列.
