18.2.3正方形课件
图片预览


文档简介
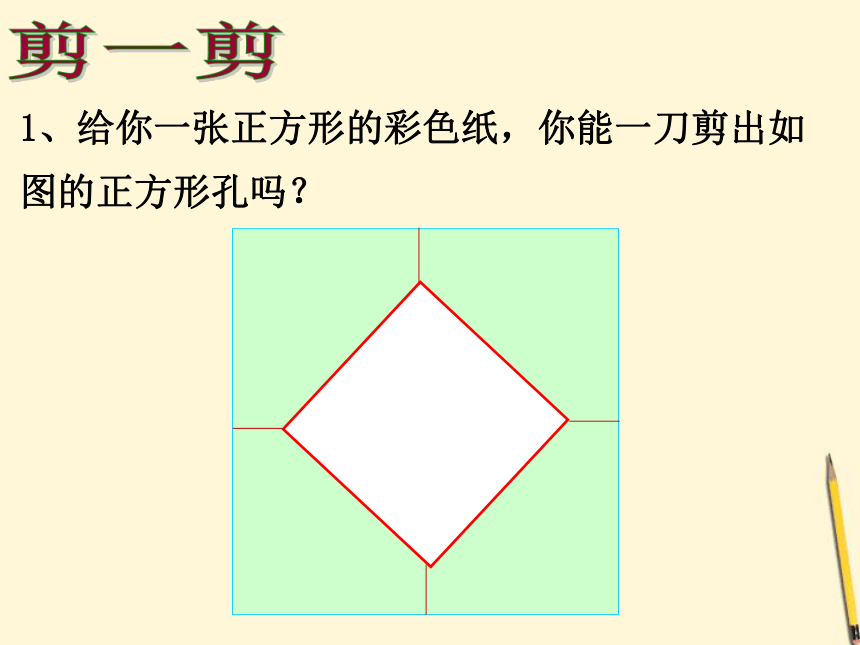
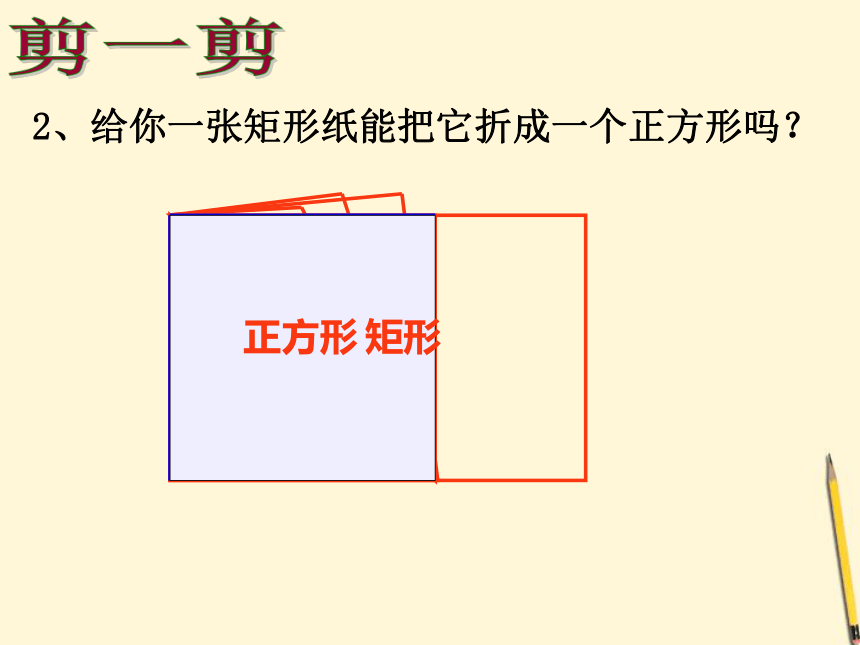
课件92张PPT。18.2.3正方形的性质与判定达连河镇第一中学:汪多敏2002年世界数学大会会标图片欣赏 剪一剪1、给你一张正方形的彩色纸,你能一刀剪出如图的正方形孔吗?正方形矩形剪一剪2、给你一张矩形纸能把它折成一个正方形吗?情景一新知探究情景一新知探究情景一新知探究情景一新知探究情景一新知探究情景一新知探究情景一新知探究 创设情景?问题: 从这个图形中你想到了什么?
ABCD情景二新知探究ABCD情景二新知探究ABCD情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究ABCD情景二新知探究ABCDAB邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形新知探究菱形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?新知探究有一个角是直角有一组邻边相等回忆如何在平行四边形的基础上来定义正方形一、正方形定义定义:一组邻边相等,且有一个角是直角的平行四边形叫做正方形菱形矩形平行四边形平行四边形,矩形,菱形,正方形的关系 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。正方形的性质=角 :四个角都是直角图形的对称性:既是轴对称图形,
又是中心对称图形.正方形的性质特殊的平行四边形
特殊的矩形
特殊的菱形
二、正方形的性质: 四条边都相等且对边平行;两条对角线互相垂直平分且相等,并且每一条对角线平分一组对角.四个角都是直角; 1、边:2. 角:3.对角线:(A)(B)(C)(D)4、既是轴对称图形也是中心对称图形有四条对称轴对称性特征正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)归纳:ACDBACDBACDB\∟∟∟∟O\\∟
对边平行 四边相等四角是直角对角线互相垂直平分且相等,每条对角线平分一组对角∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD回顾平行四边形,矩形,菱形的性质,完成表格前三列对边平行且相等四条边相等对边平行且四条边相等对角相等四个角都是直角四个角都是直角对角线互相平分对角线相等对角线互相垂直,每条对角线平分一组对角对角线相等且互相垂直平分,每条对角线平分一组对角中心对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形图形性质分类正方形类
比
归
纳 你觉得什么样的四边形是正方形呢?( 判断一个四边形是正方形有哪些方法?)正方形的判定方法:一、以平行四边形、矩形、菱形为基础定义法①四条边相等,四个角都是直角②对角线互相垂直、平分且相等二、以四边形为基础:既是菱形又是矩形的四边形是正方形。5种判
定方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等平行四边形、矩形、菱形、正方形的判定小结√√√×(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )√快速反应判断题:(6)正方形一定是矩形.( )
(7)正方形一定是菱形.( )
(8)菱形一定是正方形.( )
(9)矩形一定是正方形.( )
(10)正方形、矩形、菱形都是平行四边形. ( )√√√××(12)正方形是轴对称图形,一共有2条对称轴( )(13)四个角都相等的四边形是正方形 ( )
(14)四条边都相等的四边形是正方形 ( )×××正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD选择题:3、下列命题正确的是( )
A、四个角都相等的四边形是正方形
B、四条边都相等的四边形是正方形
C、对角线相等的平行四边形是正方形
D、对角线互相垂直的矩形是正方形D 4.四个内角都相等的四边形一定是( )
A、正方形 B、菱形 C、矩形 D平行四边形 C 5.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正 方形的是:( ) A.AO=BO=CO=DO,AC⊥BD B.AD∥BC ∠A=∠C C.AO=CO BO=DO AB=BC D.AC=BD A6 .四个内角都相等,四条边也都相等的四边形一定是:( )
A.正方形 B.菱形
C.矩形 D.平行四边形 A1、如图:正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。 7.5填空题 2.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______. 2246363.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=____cm, 43624230(7)(8)1510、正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.16cm511、已知四边形ABCD是平行四边形,对角线AC、BD相交于点O。⑴若AB=BC,则四边形ABCD是( )
⑵若AC=BD,则四边形ABCD是( )
⑶若∠BCD=900,则四边形ABCD是( )
⑷若OA=OB,则四边形ABCD是( )
⑸若AB=BC,且AC=BD,则四边形ABCD是
( )菱形矩形矩形矩形正方形例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明这是一道文字证明题,该怎么做?你会做吗?已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
1.如图,在正方形ABCD中,点E在对角线AC上,那么,BE和DE相等吗?为什么?解:BE=DE.
因为 对角线AC所在的直线是正方形ABCD的对称轴,而点E在对称轴上,点B为点D关于AC的对称点,
所以 BE=DE
练一练解:∵四边形ABCD是正方形∴AD=AB,∠DAE=∠BAE=45°又∵AE=AE∴△ADE≌△ABE(SAS)∴ED=EB 已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。又∵MN∥BC
∴∠OMN=∠1=
∠BCO=∠ONM=45° ∴OM=ON⌒1⌒2证明:
∵四边形ABCD是正方形 ∴OC=OD ,
∠COD=∠COB=90°
∠1=∠BCO=45°∴△COM≌△DON(SAS)∴DN=MCH⌒3解:DN=MC DN⊥MC(2)由△COM≌△DON得∠2=∠3又∠3+∠CMO=90°∴∠2+∠CMO=90°∴∠DHM=90°∴DN⊥MC例2 已知:如图,正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:∴OA-OM=OB-ON∴OM=ON∴∠OMN=∠1=∠3=∠ONM=45°又∵MN∥AB∠1=∠2=∠3=45°∴OA=OB AB=BC∵四边形ABCD是正方形即:AM=BN∴△ABM≌△BCN∴BM=CN已知:正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:OE=OF证明:∵ 四边形ABCD是正方形
∴∠AOE=∠DOF=90°,
AO=DO
(正 方形的对角线垂直平分且相等)
又DG⊥AE
∴∠EAO+∠AEO=∠EDG+∠AEO=90°
∴∠EAO=∠FDO
∴△AEO ≌△DFO
∴OE=OF 直角三角形ABC中∠ACB =90°,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB。求证:四边形CEDF是正方形。∴四边形ABCD是正方形( )∴ DE=DF( )DE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形( )而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥AB 有三个角是 直角 的四边形是矩形 角平分线的定理有一组邻边相等的矩形是正方形例3 已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∴DM=DF∴Rt△CDM≌Rt△ADF (ASA)又∵CD=AD,∠ADF=∠MDC=Rt∠∴∠1=∠2∵∠CMD=∠AME∴∠ADC=∠AEM=90°∵CE⊥AF 四边形ABCD是正方形∴∠MFD=45°例41、已知:如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD,延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF 练一练2、已知:如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG3、在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?4、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF,探索图中AE与BF的关系。5、如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。6、在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明) 如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师课外拓展:数一数图中正方形的个数,你发现了什么?多多多 ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识 解:∵四边形ABCD是正方形
∴AB= BC = 2cm,∠ABC = 90°
﹙正方形的四个角都是直角,四条边都相等﹚ 练习 1、已知:正方形的一条边长为2cm,求这个正方形
的周长、对角线长和正方形的面积。 ∵边长AB=2cm
∴周长C=4AB=8cm练习 2、已知:正方形的一条对角线长为4cm 解:∵四边形ABCD是正方形
∴AB = BC,∠ABC=90°
﹙正方形的四个角都是直角,四条边都相等﹚1、正方形的面积等于边长的平方。
2、正方形的面积等于对角线的平方的一半。
3、正方形的周长等于边长的4倍。 在Rt⊿ABC中,求: 它的边长和面积。练习 3、 AC为正方形ABCD的对角线,E为AC上一点,且AB=AE, EF⊥AC交BC于F.
请说明:EC=EF=FB解:∵ 四边形ABCD是正方形 ∴∠B=900 , ∠ACB=450
∵∠AEF=900 AB=AE ∴△ABF≌△AFE(HL)
∴BF=EF
又∵∠FEC=900, ∠ECF=45°
∴∠EFC=45°
∴EC=EF(等角对等边)
∴BF=EF=EC
练习 4、在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是点E、F.求证:DP=EF证明:连接PB又∵PE⊥AB , PF⊥BC∵四边形ABCD是正方形∴∠ABC=90°,AD=AB,
∠DAP=∠BAP=45°∴∠PEB=∠PFB=90°∴四边形PECF是矩形∴PB=EF又∵AP=AP∴△ADP≌△ABP(SAS)∴PD=PB∴PD=EF
练习 5、已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,如图(2)。
求:AC的长及正方形的面积S。 EFG矩形EFCG的周长。练习 6、已知:如图矩形ABCD,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,连接OE,若∠EAO=150,求∠BOE的度数。练习 7、如图,正方形ABCD的边长为8, M在DC上,且DM=2,N是AC上一个动点,求DN+MN的最小值。ABCDMN练习 8、已知,如图在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN垂足为点E,①求证:四边形ADCE是矩形。②当△ABC满足什么条件时,四边形
ADCE是正方形,说明理由。练习 9、如图B、C、E是同一直线上的三个点,四边形ABCD与CEFG是正方形,连接BG、DE(1)观察、猜想BG与DE之间的大小关系,并说明理由。(2)正方形CEFG在绕点C旋转过程中,BG与DE之间的关系是否仍然成立。练习 10、如图,M为正方形ABCD边AB的中点,E是AB延长线上一点,MN⊥DM,且交∠CBE的平分线于点N。(1)求证:MD=MN(2)若将上述条件中的“M是AB的中点”改为“M为AB上任意一点”,其它条件不变,问结论MD=MN是否仍然成立。FP●●练习 11、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,猜想AE与CG的位置
关系,并证明你的猜想。(1)证△ADE≌△CDG(SAS)(2)AE⊥CG思考题: 如图正方形ABCD的对角线相交于点O,O又是另一个正方形OEFG的一个顶点,若正方形OEFG绕点O旋转,在旋转的过程中.
探究二:若正方形OEFG与正方形ABCD两边分别相交于M N,试判断线段AM于BN之间的关系.探究一:两个正方形重叠部分的面积是否会发生变化?并说明理由。探究四: 如图,有两个大小不等的两个正 方形,其中小正方形的面积是大正方形面积的一半,若阴影部分的面积为8,则小正方形的边长为多少?探究三: 若正方形OEFG继续旋转时,AM 与
BN之间的关系是否还成立?构建与证明OBA已知:如图,分别延长等腰直角三角形OAB的两条直角边AO和BO,使AO=OC,BO=OD
求证:四边形ABCD是正方形。四条边都相等一组邻边相等对角线互相垂直对角线互相平分一组对边平行且相等两组对边分别平行或相等三个角都是直角一个角是直角对角线相等一组邻边相等 作 业12、13、15四边形2、再见! 成功就是99%的血汗,加上1%的灵感。
------爱迪生 在科学上从没有平坦的大道,只有不畏艰险勇于攀登的人,才能达到光辉的顶点------马克思练习 3、AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,
求证:EC=EF=FBABCDEF┌证明: ∵ 四边形ABCD是正方形
∴∠B=900 ∠ACB=450
∵∠AEF=900 AB=AE
∴△ABF≌△AEF(HL)
∴BF=EF
又∵∠FEC=900
∴∠EFC=450
∴EC=EF(等角对等边)
∴BF=EF=EC已知:如图在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是点E、F.
求证:DP=EF2、如图所示是一块在电脑屏幕上出现矩形色块图,由6个颜色不同的正方形组成,若中间最小的一个正方形边长为1,你能求这矩形色块的面积吗?课外拓展: 四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数.
8解:∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450 (2)若AC=4,则正方形边长 ; 正方形的面积是4㎝(3)正方形的面积64cm,则对角线交点到正方形一边的距离1、在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种) 课外拓展:小结√√√√√√√√√√√√√√√√√√√√√√已知:如图正方形ABCD对角线AC、BD相交于点O。求证: △ABO ≌ △BCO ≌ △CDO ≌△ADO 例1、求证:正方形的两条对角线把正方形分成四个
全等的等腰直角三角形。 3.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:4.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF几种特殊四边形的性质 对边平行
且相等对边平行 且相等对边平行
四边相等对边平行
四边相等对角相等
邻角互补 四个角
都是直角对角相等
邻角互补 四个角
都是直角对角线互相平分对角线相等
且互相平分对角线互相垂直平分,每条对角线平分一组对角对角线互相垂直平分且相等,每条对角线平分一组对角中心对称图形 轴对称图形
中心对称图形 轴对称图形
中心对称图形 轴对称图形
中心对称图形
ABCD情景二新知探究ABCD情景二新知探究ABCD情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究ABCD情景二新知探究ABCDAB邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形新知探究菱形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?新知探究有一个角是直角有一组邻边相等回忆如何在平行四边形的基础上来定义正方形一、正方形定义定义:一组邻边相等,且有一个角是直角的平行四边形叫做正方形菱形矩形平行四边形平行四边形,矩形,菱形,正方形的关系 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。正方形的性质=角 :四个角都是直角图形的对称性:既是轴对称图形,
又是中心对称图形.正方形的性质特殊的平行四边形
特殊的矩形
特殊的菱形
二、正方形的性质: 四条边都相等且对边平行;两条对角线互相垂直平分且相等,并且每一条对角线平分一组对角.四个角都是直角; 1、边:2. 角:3.对角线:(A)(B)(C)(D)4、既是轴对称图形也是中心对称图形有四条对称轴对称性特征正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)归纳:ACDBACDBACDB\∟∟∟∟O\\∟
对边平行 四边相等四角是直角对角线互相垂直平分且相等,每条对角线平分一组对角∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD回顾平行四边形,矩形,菱形的性质,完成表格前三列对边平行且相等四条边相等对边平行且四条边相等对角相等四个角都是直角四个角都是直角对角线互相平分对角线相等对角线互相垂直,每条对角线平分一组对角对角线相等且互相垂直平分,每条对角线平分一组对角中心对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形图形性质分类正方形类
比
归
纳 你觉得什么样的四边形是正方形呢?( 判断一个四边形是正方形有哪些方法?)正方形的判定方法:一、以平行四边形、矩形、菱形为基础定义法①四条边相等,四个角都是直角②对角线互相垂直、平分且相等二、以四边形为基础:既是菱形又是矩形的四边形是正方形。5种判
定方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等平行四边形、矩形、菱形、正方形的判定小结√√√×(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )√快速反应判断题:(6)正方形一定是矩形.( )
(7)正方形一定是菱形.( )
(8)菱形一定是正方形.( )
(9)矩形一定是正方形.( )
(10)正方形、矩形、菱形都是平行四边形. ( )√√√××(12)正方形是轴对称图形,一共有2条对称轴( )(13)四个角都相等的四边形是正方形 ( )
(14)四条边都相等的四边形是正方形 ( )×××正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD选择题:3、下列命题正确的是( )
A、四个角都相等的四边形是正方形
B、四条边都相等的四边形是正方形
C、对角线相等的平行四边形是正方形
D、对角线互相垂直的矩形是正方形D 4.四个内角都相等的四边形一定是( )
A、正方形 B、菱形 C、矩形 D平行四边形 C 5.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正 方形的是:( ) A.AO=BO=CO=DO,AC⊥BD B.AD∥BC ∠A=∠C C.AO=CO BO=DO AB=BC D.AC=BD A6 .四个内角都相等,四条边也都相等的四边形一定是:( )
A.正方形 B.菱形
C.矩形 D.平行四边形 A1、如图:正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。 7.5填空题 2.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______. 2246363.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=____cm, 43624230(7)(8)1510、正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.16cm511、已知四边形ABCD是平行四边形,对角线AC、BD相交于点O。⑴若AB=BC,则四边形ABCD是( )
⑵若AC=BD,则四边形ABCD是( )
⑶若∠BCD=900,则四边形ABCD是( )
⑷若OA=OB,则四边形ABCD是( )
⑸若AB=BC,且AC=BD,则四边形ABCD是
( )菱形矩形矩形矩形正方形例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明这是一道文字证明题,该怎么做?你会做吗?已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
1.如图,在正方形ABCD中,点E在对角线AC上,那么,BE和DE相等吗?为什么?解:BE=DE.
因为 对角线AC所在的直线是正方形ABCD的对称轴,而点E在对称轴上,点B为点D关于AC的对称点,
所以 BE=DE
练一练解:∵四边形ABCD是正方形∴AD=AB,∠DAE=∠BAE=45°又∵AE=AE∴△ADE≌△ABE(SAS)∴ED=EB 已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。又∵MN∥BC
∴∠OMN=∠1=
∠BCO=∠ONM=45° ∴OM=ON⌒1⌒2证明:
∵四边形ABCD是正方形 ∴OC=OD ,
∠COD=∠COB=90°
∠1=∠BCO=45°∴△COM≌△DON(SAS)∴DN=MCH⌒3解:DN=MC DN⊥MC(2)由△COM≌△DON得∠2=∠3又∠3+∠CMO=90°∴∠2+∠CMO=90°∴∠DHM=90°∴DN⊥MC例2 已知:如图,正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:∴OA-OM=OB-ON∴OM=ON∴∠OMN=∠1=∠3=∠ONM=45°又∵MN∥AB∠1=∠2=∠3=45°∴OA=OB AB=BC∵四边形ABCD是正方形即:AM=BN∴△ABM≌△BCN∴BM=CN已知:正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:OE=OF证明:∵ 四边形ABCD是正方形
∴∠AOE=∠DOF=90°,
AO=DO
(正 方形的对角线垂直平分且相等)
又DG⊥AE
∴∠EAO+∠AEO=∠EDG+∠AEO=90°
∴∠EAO=∠FDO
∴△AEO ≌△DFO
∴OE=OF 直角三角形ABC中∠ACB =90°,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB。求证:四边形CEDF是正方形。∴四边形ABCD是正方形( )∴ DE=DF( )DE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形( )而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥AB 有三个角是 直角 的四边形是矩形 角平分线的定理有一组邻边相等的矩形是正方形例3 已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∴DM=DF∴Rt△CDM≌Rt△ADF (ASA)又∵CD=AD,∠ADF=∠MDC=Rt∠∴∠1=∠2∵∠CMD=∠AME∴∠ADC=∠AEM=90°∵CE⊥AF 四边形ABCD是正方形∴∠MFD=45°例41、已知:如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD,延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF 练一练2、已知:如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG3、在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?4、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF,探索图中AE与BF的关系。5、如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。6、在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明) 如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师课外拓展:数一数图中正方形的个数,你发现了什么?多多多 ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识 解:∵四边形ABCD是正方形
∴AB= BC = 2cm,∠ABC = 90°
﹙正方形的四个角都是直角,四条边都相等﹚ 练习 1、已知:正方形的一条边长为2cm,求这个正方形
的周长、对角线长和正方形的面积。 ∵边长AB=2cm
∴周长C=4AB=8cm练习 2、已知:正方形的一条对角线长为4cm 解:∵四边形ABCD是正方形
∴AB = BC,∠ABC=90°
﹙正方形的四个角都是直角,四条边都相等﹚1、正方形的面积等于边长的平方。
2、正方形的面积等于对角线的平方的一半。
3、正方形的周长等于边长的4倍。 在Rt⊿ABC中,求: 它的边长和面积。练习 3、 AC为正方形ABCD的对角线,E为AC上一点,且AB=AE, EF⊥AC交BC于F.
请说明:EC=EF=FB解:∵ 四边形ABCD是正方形 ∴∠B=900 , ∠ACB=450
∵∠AEF=900 AB=AE ∴△ABF≌△AFE(HL)
∴BF=EF
又∵∠FEC=900, ∠ECF=45°
∴∠EFC=45°
∴EC=EF(等角对等边)
∴BF=EF=EC
练习 4、在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是点E、F.求证:DP=EF证明:连接PB又∵PE⊥AB , PF⊥BC∵四边形ABCD是正方形∴∠ABC=90°,AD=AB,
∠DAP=∠BAP=45°∴∠PEB=∠PFB=90°∴四边形PECF是矩形∴PB=EF又∵AP=AP∴△ADP≌△ABP(SAS)∴PD=PB∴PD=EF
练习 5、已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,如图(2)。
求:AC的长及正方形的面积S。 EFG矩形EFCG的周长。练习 6、已知:如图矩形ABCD,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,连接OE,若∠EAO=150,求∠BOE的度数。练习 7、如图,正方形ABCD的边长为8, M在DC上,且DM=2,N是AC上一个动点,求DN+MN的最小值。ABCDMN练习 8、已知,如图在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN垂足为点E,①求证:四边形ADCE是矩形。②当△ABC满足什么条件时,四边形
ADCE是正方形,说明理由。练习 9、如图B、C、E是同一直线上的三个点,四边形ABCD与CEFG是正方形,连接BG、DE(1)观察、猜想BG与DE之间的大小关系,并说明理由。(2)正方形CEFG在绕点C旋转过程中,BG与DE之间的关系是否仍然成立。练习 10、如图,M为正方形ABCD边AB的中点,E是AB延长线上一点,MN⊥DM,且交∠CBE的平分线于点N。(1)求证:MD=MN(2)若将上述条件中的“M是AB的中点”改为“M为AB上任意一点”,其它条件不变,问结论MD=MN是否仍然成立。FP●●练习 11、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,猜想AE与CG的位置
关系,并证明你的猜想。(1)证△ADE≌△CDG(SAS)(2)AE⊥CG思考题: 如图正方形ABCD的对角线相交于点O,O又是另一个正方形OEFG的一个顶点,若正方形OEFG绕点O旋转,在旋转的过程中.
探究二:若正方形OEFG与正方形ABCD两边分别相交于M N,试判断线段AM于BN之间的关系.探究一:两个正方形重叠部分的面积是否会发生变化?并说明理由。探究四: 如图,有两个大小不等的两个正 方形,其中小正方形的面积是大正方形面积的一半,若阴影部分的面积为8,则小正方形的边长为多少?探究三: 若正方形OEFG继续旋转时,AM 与
BN之间的关系是否还成立?构建与证明OBA已知:如图,分别延长等腰直角三角形OAB的两条直角边AO和BO,使AO=OC,BO=OD
求证:四边形ABCD是正方形。四条边都相等一组邻边相等对角线互相垂直对角线互相平分一组对边平行且相等两组对边分别平行或相等三个角都是直角一个角是直角对角线相等一组邻边相等 作 业12、13、15四边形2、再见! 成功就是99%的血汗,加上1%的灵感。
------爱迪生 在科学上从没有平坦的大道,只有不畏艰险勇于攀登的人,才能达到光辉的顶点------马克思练习 3、AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,
求证:EC=EF=FBABCDEF┌证明: ∵ 四边形ABCD是正方形
∴∠B=900 ∠ACB=450
∵∠AEF=900 AB=AE
∴△ABF≌△AEF(HL)
∴BF=EF
又∵∠FEC=900
∴∠EFC=450
∴EC=EF(等角对等边)
∴BF=EF=EC已知:如图在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是点E、F.
求证:DP=EF2、如图所示是一块在电脑屏幕上出现矩形色块图,由6个颜色不同的正方形组成,若中间最小的一个正方形边长为1,你能求这矩形色块的面积吗?课外拓展: 四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数.
8解:∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450 (2)若AC=4,则正方形边长 ; 正方形的面积是4㎝(3)正方形的面积64cm,则对角线交点到正方形一边的距离1、在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种) 课外拓展:小结√√√√√√√√√√√√√√√√√√√√√√已知:如图正方形ABCD对角线AC、BD相交于点O。求证: △ABO ≌ △BCO ≌ △CDO ≌△ADO 例1、求证:正方形的两条对角线把正方形分成四个
全等的等腰直角三角形。 3.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:4.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF几种特殊四边形的性质 对边平行
且相等对边平行 且相等对边平行
四边相等对边平行
四边相等对角相等
邻角互补 四个角
都是直角对角相等
邻角互补 四个角
都是直角对角线互相平分对角线相等
且互相平分对角线互相垂直平分,每条对角线平分一组对角对角线互相垂直平分且相等,每条对角线平分一组对角中心对称图形 轴对称图形
中心对称图形 轴对称图形
中心对称图形 轴对称图形
中心对称图形
