数学人教A版(2019)必修第一册5.1.1任意角(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.1任意角(共34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 28.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 16:54:28 | ||
图片预览










文档简介
(共34张PPT)
5.1 任意角与弧度制
5.1.1 任意角
过去我们学习了0°~360°范围的角,但在实际问题中还会遇到其他角.如在体操、跳水等比赛中,常常听到“转体1080°”、“转体1260°”。再如钟表的指针、拧动螺丝的扳手旋转所成的角方向不同.因此,我们必须将角的概念进行推广.
问题1 在初中是如何定义角的?角的范围是多少?
提示 角可以看成一条射线绕着它的端点旋转所成的图形,角的范围是0°~360°.
PART 1 任意角
定义:一条射线OA绕着端点O旋转到另一个位置OB, 所形成的图形为角α。
始边
终边
顶点
“角α”或“∠α”可以简记为“α”
PART 2 正角负角
角按旋转方向分类:
(1)正角:按逆时针方向旋转形成的角
(2)负角:按顺时针方向旋转形成的角
(3)零角:一条射线没有做任何旋转形成的角
把角的概念推广到任意角,角有正负之分,角的大小可以取任意值。
定义理解
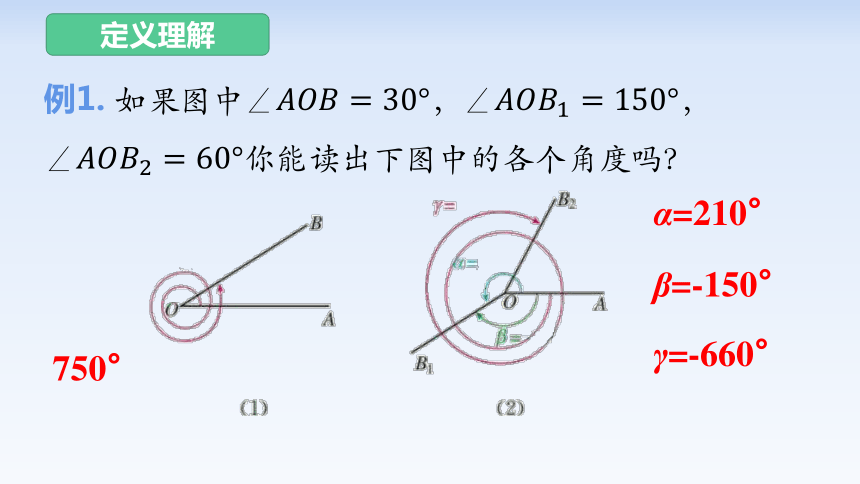
例1. 如果图中∠,∠,∠你能读出下图中的各个角度吗?
750°
α=210°
β=-150°
γ=-660°
若手表时针走过4小时,则时针转过的角度为
A.120° B.-120°
C.-60° D.60°
√
由于时针是顺时针旋转,故时针转过的角度为负数,
例1
经过2个小时,钟表的时针和分针转过的角度分别是
A.60°,720° B.-60°,-720°
C.-30°,-360° D.-60°,720°
√
PART 3 角的加减法
1.角的加法:设
是任意两个角.我们规定,把角的终边旋转角,这时终边所对应的角是.
PART 3 角的加减法
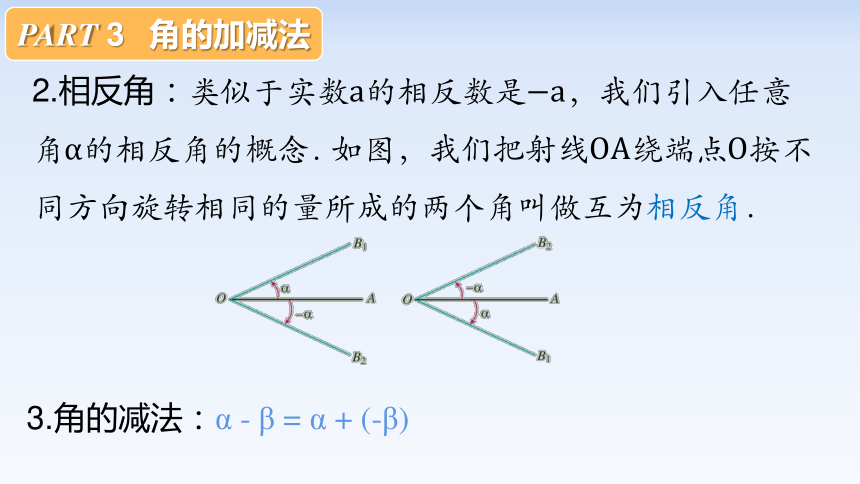
2.相反角:类似于实数的相反数是,我们引入任意角的相反角的概念.
如图,我们把射线绕端点按不同方向旋转相同的量所成的两个角叫做互为相反角.
3.角的减法:α - β = α + (-β)
定义理解
例2. 将一条射线绕着其端点顺时针旋转198°,再逆时针旋转80°,最后形成的角的度数为________
解析:∵顺时针旋转所成的角为负角,
逆时针旋转所成的角为正角,
∴经两次旋转后形成的角的度数
为 -198°+ 80°= -118°
-118°
练习. 求下列各式的值,并作图说明运算的几何意义
(1)90°+(60°)
(2)60°180°
解:(1)90°+(60°)=30° (2)60°180°=120°
60°
90°
x
y
O
x
y
O
60°
180°
问题2 现在,我们把角的概念推广到了任意角,如何更形象地表示一个角?
提示 我们通常在直角坐标系内讨论角,为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角.
PART 4 象限角/轴线角
(1)锐角是第一象限角,钝角是第二象限角,直角的终边在坐标轴上,它不属于任何一个象限.(轴线角)
(2)每一个象限都有正角和负角.
(3)无法比较两个象限角的大小.
注意点:
思考
?
1.锐角是第几象限的角?
2.第一象限角一定是锐角吗?
4.直角是象限角?还是轴线角?
3.第一象限角一定是正角吗?
第一象限角
不一定
不一定
轴线角
(多选)下列叙述不正确的是
A.三角形的内角是第一象限角或第二象限角
B.钝角是第二象限角
C.第二象限角比第一象限角大
D.小于180°的角是钝角、直角或锐角
跟踪训练2
√
√
√
直角不属于任何一个象限,故A不正确;
钝角是大于90°小于180°的角,是第二象限角,故B正确;
由于120°是第二象限角,390°是第一象限角,120°<390°,故C不正确;
由于零角和负角也小于180°,故D不正确.
画出30°,390°,-330°,观察它们有什么共同点?
思考
?
390°=30°+1×360°
-330°=30°-1×360°
PART 5 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+k·360°,k∈Z},
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(1)最小的正角;
例3
因为-1 845°=-45°+(-5)×360°,
即-1 845°角与-45°角的终边相同,
所以与角α终边相同的角的集合是
{β|β=-45°+k·360°,k∈Z},
最小的正角为315°.
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(2)最大的负角;
例3
最大的负角为-45°.
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(3)-360°~720°之间的角.
例3
-360°~720°之间的角分别是-45°,315°,675°.
终边相同的角的表示
(1)终边相同的角都可以表示成α+k·360°(k∈Z)的形式.
(2)终边相同的角相差360°的整数倍.
若角2α与240°角的终边相同,则α等于
A.120°+k·360°,k∈Z B.120°+k·180°,k∈Z
C.240°+k·360°,k∈Z D.240°+k·180°,k∈Z
跟踪训练3
√
角2α与240°角的终边相同,
则2α=240°+k·360°,k∈Z,
则α=120°+k·180°,k∈Z.
区域角以及终边在已知直线上的角的表示
已知,如图所示.(1)分别写出终边落在OA,OB位置上的角的集合;
跟踪训练4
终边落在OA位置上的角的集合为{α|α=210°+k·360°,k∈Z},终边落在OB位置上的角的集合为{α|α=300°+k·360°,k∈Z}.
(2)写出终边落在阴影部分(包括边界)的角的集合.
终边落在阴影部分(包括边界)的角的集合是{α|210°+k·360°≤α≤300°
+k·360°,k∈Z}.
(1)象限角的判定方法
①根据图象判定.利用图象实际操作时,依据是终边相同的角的思想,因为0°~360°之间的角与坐标系中的射线可建立一一对应的关系.
②将角转化到0°~360°范围内.在直角坐标平面内,在0°~360°之间没有两个角终边是相同的.
(2)表示区域角的三个步骤
第一步:先按逆时针的方向找到区域的起始和终止边界.
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α第三步:起始、终止边界对应角α,β再加上360°的整数倍,即得区域角集合.
课堂
小结
1.知识清单:
(1)正角、负角、零角的概念.
(2)终边相同的角的表示.
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°角的区别,终边相同的角的表示中漏掉k∈Z.
1.“α是锐角”是“α是第一象限角”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
1
2
3
4
√
因为α是锐角能推出α是第一象限角,
但是反之不成立,例如400°是第一象限角,但不是锐角,
所以“α是锐角”是“α是第一象限角”的充分不必要条件.
2.2 022°是
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
√
1
2
3
4
2 022°=5×360°+222°,
所以2 022°角的终边与222°角的终边相同,为第三象限角.
3.与-460°角终边相同的角可以表示成
A.460°+k·360°,k∈Z B.100°+k·360°,k∈Z
C.260°+k·360°,k∈Z D.-260°+k·360°,k∈Z
因为-460°=260°+(-2)×360°,
故与-460°角终边相同的角可以表示成260°+k·360°,k∈Z.
1
2
3
4
√
1
2
3
4
4.已知角α的终边在如图阴影表示的范围内(不包含边界),那么角α的集合是_________________________________________.
{α|45°+k·360°<α<150°+k·360°,k∈Z}
观察图形可知,角α的集合是
{α|45°+k·360°<α<150°+k·360°,k∈Z}.
5.1 任意角与弧度制
5.1.1 任意角
过去我们学习了0°~360°范围的角,但在实际问题中还会遇到其他角.如在体操、跳水等比赛中,常常听到“转体1080°”、“转体1260°”。再如钟表的指针、拧动螺丝的扳手旋转所成的角方向不同.因此,我们必须将角的概念进行推广.
问题1 在初中是如何定义角的?角的范围是多少?
提示 角可以看成一条射线绕着它的端点旋转所成的图形,角的范围是0°~360°.
PART 1 任意角
定义:一条射线OA绕着端点O旋转到另一个位置OB, 所形成的图形为角α。
始边
终边
顶点
“角α”或“∠α”可以简记为“α”
PART 2 正角负角
角按旋转方向分类:
(1)正角:按逆时针方向旋转形成的角
(2)负角:按顺时针方向旋转形成的角
(3)零角:一条射线没有做任何旋转形成的角
把角的概念推广到任意角,角有正负之分,角的大小可以取任意值。
定义理解
例1. 如果图中∠,∠,∠你能读出下图中的各个角度吗?
750°
α=210°
β=-150°
γ=-660°
若手表时针走过4小时,则时针转过的角度为
A.120° B.-120°
C.-60° D.60°
√
由于时针是顺时针旋转,故时针转过的角度为负数,
例1
经过2个小时,钟表的时针和分针转过的角度分别是
A.60°,720° B.-60°,-720°
C.-30°,-360° D.-60°,720°
√
PART 3 角的加减法
1.角的加法:设
是任意两个角.我们规定,把角的终边旋转角,这时终边所对应的角是.
PART 3 角的加减法
2.相反角:类似于实数的相反数是,我们引入任意角的相反角的概念.
如图,我们把射线绕端点按不同方向旋转相同的量所成的两个角叫做互为相反角.
3.角的减法:α - β = α + (-β)
定义理解
例2. 将一条射线绕着其端点顺时针旋转198°,再逆时针旋转80°,最后形成的角的度数为________
解析:∵顺时针旋转所成的角为负角,
逆时针旋转所成的角为正角,
∴经两次旋转后形成的角的度数
为 -198°+ 80°= -118°
-118°
练习. 求下列各式的值,并作图说明运算的几何意义
(1)90°+(60°)
(2)60°180°
解:(1)90°+(60°)=30° (2)60°180°=120°
60°
90°
x
y
O
x
y
O
60°
180°
问题2 现在,我们把角的概念推广到了任意角,如何更形象地表示一个角?
提示 我们通常在直角坐标系内讨论角,为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角.
PART 4 象限角/轴线角
(1)锐角是第一象限角,钝角是第二象限角,直角的终边在坐标轴上,它不属于任何一个象限.(轴线角)
(2)每一个象限都有正角和负角.
(3)无法比较两个象限角的大小.
注意点:
思考
?
1.锐角是第几象限的角?
2.第一象限角一定是锐角吗?
4.直角是象限角?还是轴线角?
3.第一象限角一定是正角吗?
第一象限角
不一定
不一定
轴线角
(多选)下列叙述不正确的是
A.三角形的内角是第一象限角或第二象限角
B.钝角是第二象限角
C.第二象限角比第一象限角大
D.小于180°的角是钝角、直角或锐角
跟踪训练2
√
√
√
直角不属于任何一个象限,故A不正确;
钝角是大于90°小于180°的角,是第二象限角,故B正确;
由于120°是第二象限角,390°是第一象限角,120°<390°,故C不正确;
由于零角和负角也小于180°,故D不正确.
画出30°,390°,-330°,观察它们有什么共同点?
思考
?
390°=30°+1×360°
-330°=30°-1×360°
PART 5 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+k·360°,k∈Z},
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(1)最小的正角;
例3
因为-1 845°=-45°+(-5)×360°,
即-1 845°角与-45°角的终边相同,
所以与角α终边相同的角的集合是
{β|β=-45°+k·360°,k∈Z},
最小的正角为315°.
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(2)最大的负角;
例3
最大的负角为-45°.
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(3)-360°~720°之间的角.
例3
-360°~720°之间的角分别是-45°,315°,675°.
终边相同的角的表示
(1)终边相同的角都可以表示成α+k·360°(k∈Z)的形式.
(2)终边相同的角相差360°的整数倍.
若角2α与240°角的终边相同,则α等于
A.120°+k·360°,k∈Z B.120°+k·180°,k∈Z
C.240°+k·360°,k∈Z D.240°+k·180°,k∈Z
跟踪训练3
√
角2α与240°角的终边相同,
则2α=240°+k·360°,k∈Z,
则α=120°+k·180°,k∈Z.
区域角以及终边在已知直线上的角的表示
已知,如图所示.(1)分别写出终边落在OA,OB位置上的角的集合;
跟踪训练4
终边落在OA位置上的角的集合为{α|α=210°+k·360°,k∈Z},终边落在OB位置上的角的集合为{α|α=300°+k·360°,k∈Z}.
(2)写出终边落在阴影部分(包括边界)的角的集合.
终边落在阴影部分(包括边界)的角的集合是{α|210°+k·360°≤α≤300°
+k·360°,k∈Z}.
(1)象限角的判定方法
①根据图象判定.利用图象实际操作时,依据是终边相同的角的思想,因为0°~360°之间的角与坐标系中的射线可建立一一对应的关系.
②将角转化到0°~360°范围内.在直角坐标平面内,在0°~360°之间没有两个角终边是相同的.
(2)表示区域角的三个步骤
第一步:先按逆时针的方向找到区域的起始和终止边界.
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α
课堂
小结
1.知识清单:
(1)正角、负角、零角的概念.
(2)终边相同的角的表示.
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°角的区别,终边相同的角的表示中漏掉k∈Z.
1.“α是锐角”是“α是第一象限角”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
1
2
3
4
√
因为α是锐角能推出α是第一象限角,
但是反之不成立,例如400°是第一象限角,但不是锐角,
所以“α是锐角”是“α是第一象限角”的充分不必要条件.
2.2 022°是
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
√
1
2
3
4
2 022°=5×360°+222°,
所以2 022°角的终边与222°角的终边相同,为第三象限角.
3.与-460°角终边相同的角可以表示成
A.460°+k·360°,k∈Z B.100°+k·360°,k∈Z
C.260°+k·360°,k∈Z D.-260°+k·360°,k∈Z
因为-460°=260°+(-2)×360°,
故与-460°角终边相同的角可以表示成260°+k·360°,k∈Z.
1
2
3
4
√
1
2
3
4
4.已知角α的终边在如图阴影表示的范围内(不包含边界),那么角α的集合是_________________________________________.
{α|45°+k·360°<α<150°+k·360°,k∈Z}
观察图形可知,角α的集合是
{α|45°+k·360°<α<150°+k·360°,k∈Z}.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
