苏教版六年级下册数学总复习 数与代数 分数和百分数的认识课件(共38张ppt)
文档属性
| 名称 | 苏教版六年级下册数学总复习 数与代数 分数和百分数的认识课件(共38张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 16:48:55 | ||
图片预览










文档简介
总复习
1.数与代数
分数和百分数的认识
七
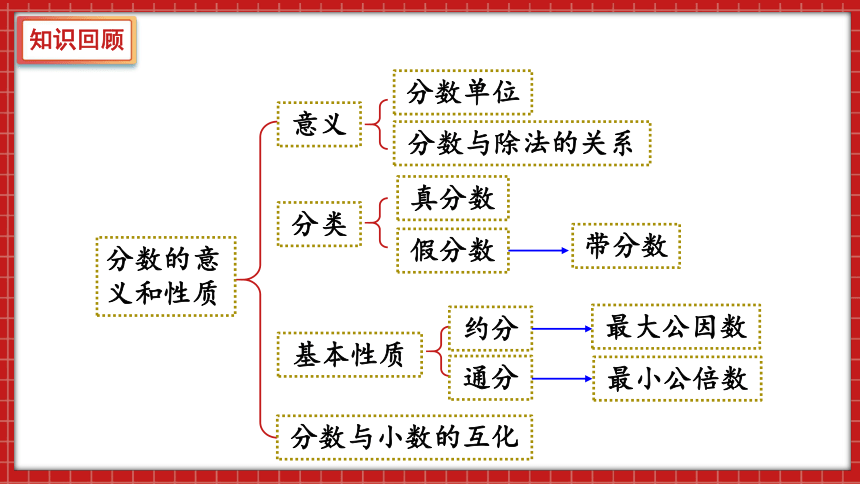
分数的意义和性质
意义
基本性质
分数单位
分数与除法的关系
分类
真分数
假分数
约分
通分
分数与小数的互化
带分数
最大公因数
最小公倍数
知识回顾
(教材第71页)
把单位“ 1”平均分成若干份,表示这样一份或几份的数叫作分数。
百分数是一种特殊的分数,它只表示一个数是另一个数的百分之几。
你了解分数、百分数的哪些知识?
分数
把单位“1”平均分成若干份,表示这
样的一份或几份的数叫作分数。
分数单位
分母
分子
表示把单位“1”平均分的份数
表示有这样的几份
分数
真分数
分子<分母
假分数
真分数<1
分子≥分母
假分数≥1
分子是分母的倍数
整数
分子不是
分母的倍数
带分数
整数和真分数合成
百分数
百分数与分数
表示一个数是另一个数的百分之几的数
叫作百分数(也叫百分率或百分比)。
百分数的计数单位是 。
1
100
联系:百分数是分母为100的特殊分数。
区别:(1)分数由分子、分母和分数线组成,而百分数通常采用“%”来表示。(2)分数既可以表示一个具体的数量(可以加单位名称),也可以表示两个数量之间的倍比关系;百分数只表示两个数或数量的倍比关系(不可以加单位名称)。
读法和写法——分数
读法:
先读分母,再将分数线读作“分之”,最后读分子。
分子和分母分别按照整数的读法来读。
读带分数时,先读整数部分,再读分数部分,中间加一个“又”字。
读法和写法——分数
写法:
先写分数线,再写分母,最后写分子。
写带分数时,先写整数部分,再写分数部分,整数部分要对准分数线,距离要紧凑。
在列式计算中,分数线要对准“=”中两横线的中间。
读法和写法——百分数
读法:
先读百分号,读作“百分之”,再读百分号前面的数。
写法:
先写分子,再写百分号。
百分数通常不写成分数形式,而是在原来的分子后面加上“%”。
把3块饼平均分成4份,求每份的数量,列式为3÷4 = (块)。
4
3
把3块饼看作单位“1”,平均分成4份,求每份所占的份数,列式为1÷4 = 。
4
1
分数与除法有什么联系?你能举例说明吗?
分数与除法的关系:被除数÷除数=
被除数
除数
把3块饼平均分给4位同学,每人分得3块饼的( ),每人分得( )块。
4
1
4
3
分数的分子和分母同时乘或者除以相同的数
(0除外),分数的大小不变。这是分数的基本性质。
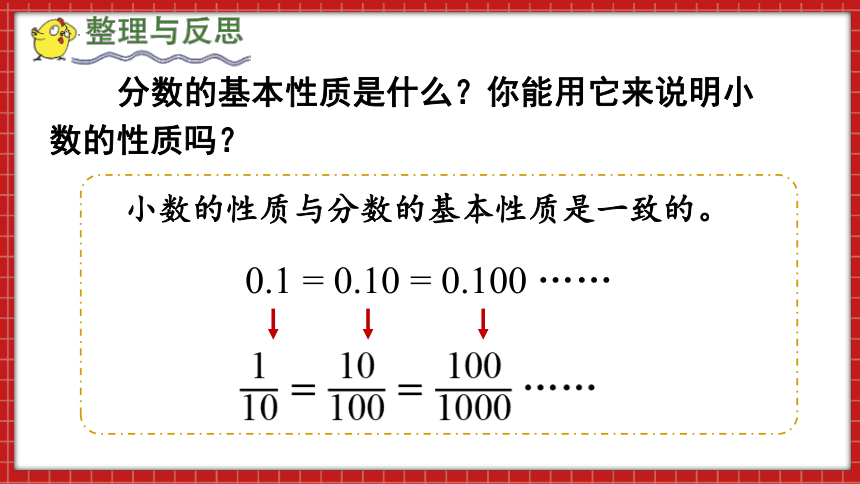
分数的基本性质是什么?你能用它来说明小数的性质吗?
小数可以看作分母为10、100、1000,…的分数。
分数的基本性质是什么?你能用它来说明小数的性质吗?
0.1 = 0.10 = 0.100 ……
110=10100=1001000 ……
?
小数的性质与分数的基本性质是一致的。
先改写成分母是10,100,1000,…的分数,再约分
用分子除以分母,除不尽的一般保留两位小数
小数点向右移两位,加上“%”
小数点向左移两位,去掉“%”
写成分数形式,并约分
先改写成小数,再改写成百分数
小数
分数
百分数
小数、分数和百分数怎样互相改写?
除不尽的一般保留三位小数
(教材第71页)
1.分别用分数、小数和百分数表示图中的涂色部分。
分数( )
小数( )
百分数( )
分数( )
小数( )
百分数( )
分数( )
小数( )
百分数( )
0.3
30%
0.03
3%
0.003
0.3%
????????????
?
????????????????
?
????????????????????
?
2.
(1)3÷5= = = =( )%
15
( )
25
10
60
( )
15
( )
( )
9
6
(2)把一根3米长的绳子剪成同样长的8段,每段长是全长的 ,每段长 米。
( )
( )
( )
( )
8
1
8
3
3.把30%、 100%、 3%、 115% 填入合适的括号里。
(1)六年级116名同学今天全部到校,出勤率是
( )。
100%
(2)这几年小军的身高平均每年大约增长 ( )。
3%
(3)长江比黄河长,长江的长度大约相当于黄河的
( )。
(4)一件商品比原价便宜很多,降价的幅度达( )。
30%
115%
4.
75%
0.4
120%
40%
分 数
小 数
百分数
0.75
1.2
????????
?
????????
?
????????
?
5. 在括号里填适当的数。
(1)0.9 ,0.99 ,0.999,( ),( ), …
0.9999
(2)????????,????????,????????,(?????????),( ),…
?
0.99999
上面两组数分别会越来越接近几?
????????????
?
????????????
?
越来越接近1
越来越接近0
6.下图表示5块花圃,涂色部分种玫瑰。 先估计哪个花圃种玫瑰的面积所占的百分比最大,再写出相应的百分数,看看估计得对不对。
66.7%
62.5%
①
②
③
④
⑤
60%
75%
71.4%
所占的百分比最大
7.用100 粒种子做发芽试验,有13粒未发芽。求种子的发芽率。
方法一
100-13 = 87(粒)
87÷100 = 87%
方法二
13÷100 = 13%
100%-13 %= 87%
答:种子的发芽率是87% 。
8.商店有一件上衣,原价150元,现价120元。这件上衣是打几折出售的?
120÷150 = 0.8 = 80%
答:这件上衣是打八折出售的。
9. 李华家上个月的支出情况如下:伙食费占40%,水、电、煤气和电话费占10%,教育支出占10%,购物占25%,其他支出占15%。
(1)在右图中表示出李华家上个月
的支出情况。
(2)向家长了解自己家一个月的收
入和各项支出情况,计算主要支出
各占收入的百分之几。
伙食费
40%
购物
25%
水、电、煤气
和电话费
10%
教育
10%
其他
15%
10.从报刊、网络等媒体上收集一些用分数或百分数表示的信息,与同学交流,并说说你对这些信息的理解。
1.李时珍在《本草纲目》中记载了1800多种草药,在武当山就能找到其中的800多种。你认为选择什么数描述这两种数量之间的关系比较合适?说说你的理由。
选择用百分数表示这两种数量关系比较合适,因为百分数能够反映出武当山所产的草药数量占《本草纲目》中记载草药数量的多少。
巩固练习
2.(1)分数单位是????????的最大真分数是( ),最小假分数是( )。
?
7
8
8
8
分数单位是 即分母是8,真分数的分子小于分母,最大为7;假分数的分子大于或等于分母,最小为8。
1
8
(2)35÷( )= =( )%=( )成
7
10
这道题从 入手思考,根据分数和除法的关系和商不变的规律得 =7÷10=35÷50。
7
10
7
10
50
70
七
(3)下面直线上的点A表示的数是( ),点B表示的数写成小数是( ),点C表示的数写成分数是 。
( )
( )
通过观察可知:点A距离0点1个单位长度,在0的左边是负数,所以点A表示的数是-1。
-1
0.5
5
8
0
-3
1
2
-2
A
B
C
点B在0和1的中间,将1个单位长度平均分成了2份,所以点B表示的小数是0.5。
点C在1和2之间,将1个单位长度平均分成了5份,表示其中的3份,所以点C表示的分数是 ,也就是 。
3
5
1
8
5
(1)如果a>b,且a和b都是不等于0的自然数,
那么 一定小于 。 ( )
b
2a
a
ab
3.判一判。
×
分数的
大小比较
分母相同,分子大的分数大。
分子相同,分母小的分数大。
分子分母都不相同,先通分再比较。
= =
a
ab
a×2
ab×2
2a
2ab
b
2a
b×b
2a×b
b2
2ab
= =
当a=2,b=1时,b2<2a
当a=8,b=4时,b2=2a
当a=5,b=4时,b2>2a
(2)一个数的末尾添上0或去掉0,这个数的大小不变。 ( )
(3)把一个分数约分后,分数的大小和分数单位都不变。 ( )
×
×
只有小数的末尾添上0或去掉0大小才不变。
分母发生变化,分数单位就会发生变化。
4.如图,在正方形ABCD中,点E、F分别为BC、CD的中点,则图中涂色部分的面积占原正方形面积的 。
( )
( )
D
A
C
E
B
原正方形的
1
8
F
原正方形的
1
4
原正方形的
1
4
涂色部分的面积就是原正方形的面积减去其他部分的面积:
1- - -
=
1
4
1
4
1
8
3
8
3
8
5. 把下列各数按从大到小的顺序排列起来。
7
4
2
16
11
6
13
2.35
2.035
7
4
2
7
18
=
= 18÷7
≈ 2.571
6
13
= 13÷6
≈ 2.167
16
11
= 11÷16
= 0.6875
因为2.571>2.35>2.167>2.035>0.6875
所以 >2.35> >2.035>
7
4
2
6
13
16
11
6.
要求李阿姨和王叔叔谁打字快些,可以比较两人每秒打字的个数,即0.9和 的大小;也可以比较两人1分钟打字的多少。
6
5
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
6
5
6
5
= 5÷6
≈ 0.83
0.9>0.83
0.9>
6
5
答:李阿姨打字快些。
方法一
6.
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
6
5
0.9×60
= 54(个)
54>50
答:李阿姨打字快些。
6.
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
5
6
方法二
5
6
×60
= 50(个)
7.
路程=速度×时间
速度相同,行走的时间越长,离学校就越远。
思路一:把两人用的时间都用“小时”作单位,再通分比较。
思路二:把两人用的时间都用“分”作单位,再比较。
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些?
4
1
方法一
25÷60
=
60
25
=
12
5
4
1
=
12
3
12
5
>
12
3
答:小林家离学校远些。
7.
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些?
4
1
60分÷4
4
1
小时
=
>
15分
=
25分
15分
答:小林家离学校远些。
7.
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些?
4
1
方法二
1. 在 < < 中,n对应的整数有多少个?
分子相同,分母大的分数反而小。
确定n对应的整数的范围和个数。
4
1
8
1
n
6
将 和 都化成分子是6的分数。
8
1
4
1
拓展提升
1. 在 < < 中,n对应的整数有多少个?
4
1
8
1
n
6
48
6
8
1
=
48
6
<
n
6
<
24
6
答:n对应的整数有25,26,27,…,47,共23个。
24
6
4
1
=
48>n>24
2. 在下面的□里填一个数字(0除外),可以填几?
15
□
< 0.4
一个分数,一个小数,无法直接比较。
将0.4转化为分母是15的分数。
根据同分母分数大小比较的规律确定□里的数。
2. 在下面的□里填一个数字(0除外),可以填几?
15
□
< 0.4
0.4
4
10
=
=
12
30
=
6
15
15
□
<
6
15
□里可填大于0而小于6的自然数。
由 可知,
答:可以填1, 2, 3, 4, 5。
1.数与代数
分数和百分数的认识
七
分数的意义和性质
意义
基本性质
分数单位
分数与除法的关系
分类
真分数
假分数
约分
通分
分数与小数的互化
带分数
最大公因数
最小公倍数
知识回顾
(教材第71页)
把单位“ 1”平均分成若干份,表示这样一份或几份的数叫作分数。
百分数是一种特殊的分数,它只表示一个数是另一个数的百分之几。
你了解分数、百分数的哪些知识?
分数
把单位“1”平均分成若干份,表示这
样的一份或几份的数叫作分数。
分数单位
分母
分子
表示把单位“1”平均分的份数
表示有这样的几份
分数
真分数
分子<分母
假分数
真分数<1
分子≥分母
假分数≥1
分子是分母的倍数
整数
分子不是
分母的倍数
带分数
整数和真分数合成
百分数
百分数与分数
表示一个数是另一个数的百分之几的数
叫作百分数(也叫百分率或百分比)。
百分数的计数单位是 。
1
100
联系:百分数是分母为100的特殊分数。
区别:(1)分数由分子、分母和分数线组成,而百分数通常采用“%”来表示。(2)分数既可以表示一个具体的数量(可以加单位名称),也可以表示两个数量之间的倍比关系;百分数只表示两个数或数量的倍比关系(不可以加单位名称)。
读法和写法——分数
读法:
先读分母,再将分数线读作“分之”,最后读分子。
分子和分母分别按照整数的读法来读。
读带分数时,先读整数部分,再读分数部分,中间加一个“又”字。
读法和写法——分数
写法:
先写分数线,再写分母,最后写分子。
写带分数时,先写整数部分,再写分数部分,整数部分要对准分数线,距离要紧凑。
在列式计算中,分数线要对准“=”中两横线的中间。
读法和写法——百分数
读法:
先读百分号,读作“百分之”,再读百分号前面的数。
写法:
先写分子,再写百分号。
百分数通常不写成分数形式,而是在原来的分子后面加上“%”。
把3块饼平均分成4份,求每份的数量,列式为3÷4 = (块)。
4
3
把3块饼看作单位“1”,平均分成4份,求每份所占的份数,列式为1÷4 = 。
4
1
分数与除法有什么联系?你能举例说明吗?
分数与除法的关系:被除数÷除数=
被除数
除数
把3块饼平均分给4位同学,每人分得3块饼的( ),每人分得( )块。
4
1
4
3
分数的分子和分母同时乘或者除以相同的数
(0除外),分数的大小不变。这是分数的基本性质。
分数的基本性质是什么?你能用它来说明小数的性质吗?
小数可以看作分母为10、100、1000,…的分数。
分数的基本性质是什么?你能用它来说明小数的性质吗?
0.1 = 0.10 = 0.100 ……
110=10100=1001000 ……
?
小数的性质与分数的基本性质是一致的。
先改写成分母是10,100,1000,…的分数,再约分
用分子除以分母,除不尽的一般保留两位小数
小数点向右移两位,加上“%”
小数点向左移两位,去掉“%”
写成分数形式,并约分
先改写成小数,再改写成百分数
小数
分数
百分数
小数、分数和百分数怎样互相改写?
除不尽的一般保留三位小数
(教材第71页)
1.分别用分数、小数和百分数表示图中的涂色部分。
分数( )
小数( )
百分数( )
分数( )
小数( )
百分数( )
分数( )
小数( )
百分数( )
0.3
30%
0.03
3%
0.003
0.3%
????????????
?
????????????????
?
????????????????????
?
2.
(1)3÷5= = = =( )%
15
( )
25
10
60
( )
15
( )
( )
9
6
(2)把一根3米长的绳子剪成同样长的8段,每段长是全长的 ,每段长 米。
( )
( )
( )
( )
8
1
8
3
3.把30%、 100%、 3%、 115% 填入合适的括号里。
(1)六年级116名同学今天全部到校,出勤率是
( )。
100%
(2)这几年小军的身高平均每年大约增长 ( )。
3%
(3)长江比黄河长,长江的长度大约相当于黄河的
( )。
(4)一件商品比原价便宜很多,降价的幅度达( )。
30%
115%
4.
75%
0.4
120%
40%
分 数
小 数
百分数
0.75
1.2
????????
?
????????
?
????????
?
5. 在括号里填适当的数。
(1)0.9 ,0.99 ,0.999,( ),( ), …
0.9999
(2)????????,????????,????????,(?????????),( ),…
?
0.99999
上面两组数分别会越来越接近几?
????????????
?
????????????
?
越来越接近1
越来越接近0
6.下图表示5块花圃,涂色部分种玫瑰。 先估计哪个花圃种玫瑰的面积所占的百分比最大,再写出相应的百分数,看看估计得对不对。
66.7%
62.5%
①
②
③
④
⑤
60%
75%
71.4%
所占的百分比最大
7.用100 粒种子做发芽试验,有13粒未发芽。求种子的发芽率。
方法一
100-13 = 87(粒)
87÷100 = 87%
方法二
13÷100 = 13%
100%-13 %= 87%
答:种子的发芽率是87% 。
8.商店有一件上衣,原价150元,现价120元。这件上衣是打几折出售的?
120÷150 = 0.8 = 80%
答:这件上衣是打八折出售的。
9. 李华家上个月的支出情况如下:伙食费占40%,水、电、煤气和电话费占10%,教育支出占10%,购物占25%,其他支出占15%。
(1)在右图中表示出李华家上个月
的支出情况。
(2)向家长了解自己家一个月的收
入和各项支出情况,计算主要支出
各占收入的百分之几。
伙食费
40%
购物
25%
水、电、煤气
和电话费
10%
教育
10%
其他
15%
10.从报刊、网络等媒体上收集一些用分数或百分数表示的信息,与同学交流,并说说你对这些信息的理解。
1.李时珍在《本草纲目》中记载了1800多种草药,在武当山就能找到其中的800多种。你认为选择什么数描述这两种数量之间的关系比较合适?说说你的理由。
选择用百分数表示这两种数量关系比较合适,因为百分数能够反映出武当山所产的草药数量占《本草纲目》中记载草药数量的多少。
巩固练习
2.(1)分数单位是????????的最大真分数是( ),最小假分数是( )。
?
7
8
8
8
分数单位是 即分母是8,真分数的分子小于分母,最大为7;假分数的分子大于或等于分母,最小为8。
1
8
(2)35÷( )= =( )%=( )成
7
10
这道题从 入手思考,根据分数和除法的关系和商不变的规律得 =7÷10=35÷50。
7
10
7
10
50
70
七
(3)下面直线上的点A表示的数是( ),点B表示的数写成小数是( ),点C表示的数写成分数是 。
( )
( )
通过观察可知:点A距离0点1个单位长度,在0的左边是负数,所以点A表示的数是-1。
-1
0.5
5
8
0
-3
1
2
-2
A
B
C
点B在0和1的中间,将1个单位长度平均分成了2份,所以点B表示的小数是0.5。
点C在1和2之间,将1个单位长度平均分成了5份,表示其中的3份,所以点C表示的分数是 ,也就是 。
3
5
1
8
5
(1)如果a>b,且a和b都是不等于0的自然数,
那么 一定小于 。 ( )
b
2a
a
ab
3.判一判。
×
分数的
大小比较
分母相同,分子大的分数大。
分子相同,分母小的分数大。
分子分母都不相同,先通分再比较。
= =
a
ab
a×2
ab×2
2a
2ab
b
2a
b×b
2a×b
b2
2ab
= =
当a=2,b=1时,b2<2a
当a=8,b=4时,b2=2a
当a=5,b=4时,b2>2a
(2)一个数的末尾添上0或去掉0,这个数的大小不变。 ( )
(3)把一个分数约分后,分数的大小和分数单位都不变。 ( )
×
×
只有小数的末尾添上0或去掉0大小才不变。
分母发生变化,分数单位就会发生变化。
4.如图,在正方形ABCD中,点E、F分别为BC、CD的中点,则图中涂色部分的面积占原正方形面积的 。
( )
( )
D
A
C
E
B
原正方形的
1
8
F
原正方形的
1
4
原正方形的
1
4
涂色部分的面积就是原正方形的面积减去其他部分的面积:
1- - -
=
1
4
1
4
1
8
3
8
3
8
5. 把下列各数按从大到小的顺序排列起来。
7
4
2
16
11
6
13
2.35
2.035
7
4
2
7
18
=
= 18÷7
≈ 2.571
6
13
= 13÷6
≈ 2.167
16
11
= 11÷16
= 0.6875
因为2.571>2.35>2.167>2.035>0.6875
所以 >2.35> >2.035>
7
4
2
6
13
16
11
6.
要求李阿姨和王叔叔谁打字快些,可以比较两人每秒打字的个数,即0.9和 的大小;也可以比较两人1分钟打字的多少。
6
5
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
6
5
6
5
= 5÷6
≈ 0.83
0.9>0.83
0.9>
6
5
答:李阿姨打字快些。
方法一
6.
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
6
5
0.9×60
= 54(个)
54>50
答:李阿姨打字快些。
6.
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
5
6
方法二
5
6
×60
= 50(个)
7.
路程=速度×时间
速度相同,行走的时间越长,离学校就越远。
思路一:把两人用的时间都用“小时”作单位,再通分比较。
思路二:把两人用的时间都用“分”作单位,再比较。
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些?
4
1
方法一
25÷60
=
60
25
=
12
5
4
1
=
12
3
12
5
>
12
3
答:小林家离学校远些。
7.
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些?
4
1
60分÷4
4
1
小时
=
>
15分
=
25分
15分
答:小林家离学校远些。
7.
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些?
4
1
方法二
1. 在 < < 中,n对应的整数有多少个?
分子相同,分母大的分数反而小。
确定n对应的整数的范围和个数。
4
1
8
1
n
6
将 和 都化成分子是6的分数。
8
1
4
1
拓展提升
1. 在 < < 中,n对应的整数有多少个?
4
1
8
1
n
6
48
6
8
1
=
48
6
<
n
6
<
24
6
答:n对应的整数有25,26,27,…,47,共23个。
24
6
4
1
=
48>n>24
2. 在下面的□里填一个数字(0除外),可以填几?
15
□
< 0.4
一个分数,一个小数,无法直接比较。
将0.4转化为分母是15的分数。
根据同分母分数大小比较的规律确定□里的数。
2. 在下面的□里填一个数字(0除外),可以填几?
15
□
< 0.4
0.4
4
10
=
=
12
30
=
6
15
15
□
<
6
15
□里可填大于0而小于6的自然数。
由 可知,
答:可以填1, 2, 3, 4, 5。
