24.1.1圆

(共23张PPT)
24.1.1 圆
生活中常见的图形
问题：
体育课上，需要我们在操场上画一个半径为5m的圆，该如何画？
作一个圆需要哪些条件？
1、确定圆的位置
2、确定圆的大小
要确定一个圆,必须确定圆的____和____
圆心
半径
观察:画圆的过程，你能由此说出圆的形成过程吗？
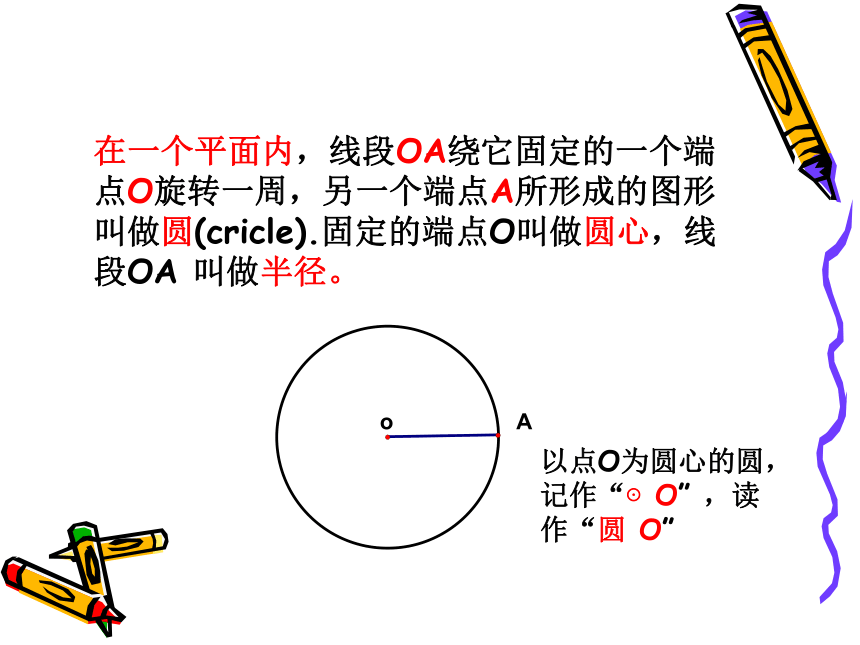
在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆(cricle).固定的端点O叫做圆心，线段OA 叫做半径。
以点O为圆心的圆，记作“⊙O” ，读作“圆 O”
从画圆的过程，我们可以得到结论：
1、圆上各点到定点（圆心O）的距离都等于定长（半径r）。
2、到定点的距离等于定长的点都在同一个圆上。
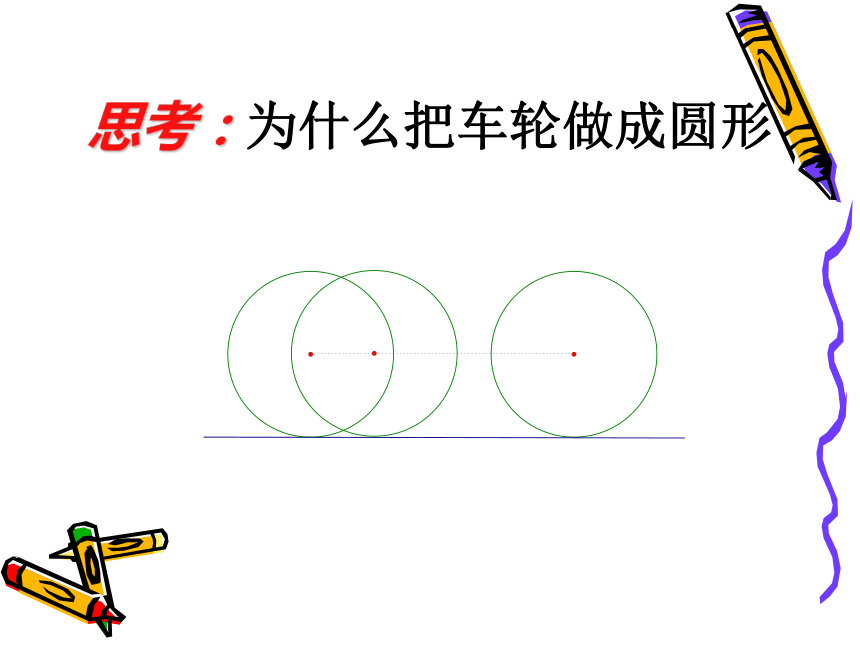
思考：为什么把车轮做成圆形
圆形车轮为什么平稳
车轮边缘上任意两点到轴心的距离都相等, 任意一点到轴心的距离是一个定值.
（圆的旋转不变性）
圆上的点到圆心的距离是一个定值
和圆有关的概念
阅读课本84、85页《圆》
1、认识圆的，了解圆的描述性定义
2、了解和圆有关的概念。
连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。
O
·
直径 d
弦
和圆有关的概念
A
B
C
活动& 探索

C
B
O
A
F
E
D
M
观察右图，回答下列问题：
（1）图中⊙O的弦有哪些？
（2） FC是弦吗？为什么？PQ呢？OE呢？为什么？
p
Q
●
O
B
C
A
1.如图,半径有:______________
OA、OB、OC
若∠AOB=60°，
则△AOB是_____三角形.
2.如图,弦有:______________
AB、BC 、AC
在圆中有长度不等的弦
等边
3、______是圆中最长的弦。
直径
圆上任意两点间的部分叫做圆弧，简称弧。以A、B为端点的弧记作AB，读做“圆弧AB”、或“弧AB”
其中像 BC这样小于半圆的圆弧叫做劣弧 ，像弧 BAC 这样的大于半圆的圆弧叫做优弧。
⌒
⌒
⌒
请指出：弧AC、
弧BC、弧ABC、弧AB、弧ACB
●
O
B
C
A
如图,列举图中的弧有:______________
⌒
AB
⌒
BC
⌒
ABC
⌒
CAB
⌒
BCA
它们一样么？
⌒
AB
⌒
BC
劣弧有：
优弧有：
⌒
ACB
⌒
BAC
你知道优弧与劣弧的区别么？
判断：
(1)直径是弦;　　　　　　
弦是直径;
等圆的半径相等;
半圆是弧，但弧不一定是半圆. 　
(√).
(√).
(×).
(√).
练习：
从树木的年轮可以很清楚地看出树木生长的年龄。如果一棵20年树龄的红杉树的树干直径是23cm，这个红杉树的半径平均每年增加多少？
巩固练习：
1、如图：CD为⊙O直径，AE交⊙O于B，且AB=OC，∠A=200,求∠DOE的度数.
巩固练习：
2 、如图：AB,CD为⊙O的直径，DE∥AB, ∠EOD=100°,求∠AOC的度数。
　　　
　　　　　　
　　　　　
巩固练习：
３、如图：以O为圆心的同心圆，大圆的弦AB交小圆于C,D两点。求证:(1)AC=BD;
(2) ∠AOC=∠BOD.
E
课堂小结
通过本节课的学习，你有哪些收获？