3.3 用图象表示的变量间关系(第1课时) 课件(共32张PPT)
文档属性
| 名称 | 3.3 用图象表示的变量间关系(第1课时) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览





文档简介
(共32张PPT)
3.3 用图象表示的变量间关系
第1课时
学习目标
1)结合具体情境,能理解图象上的点所表示的意义。
2)能从图象中获取变量之间关系的信息,并对未来的情况进行预测。
重点
能够从曲线型图象中获取关于两个变量的信息。
难点
从已知图象中发现变量之间存在的关系,并能将图中的有用信息读取出来。
我们已经学习了几种表示变量之间关系的方法
变量之间关系的表示 特征
列表法 能看出两个变量之间的变化关系
关系式法 给定一个变量的值可求出另一个变量的值
1.“五一”黄金周中,若用x表示七天假期中已过的天数,y表示所剩天数,则y与x的关系式可表示为:
y =7-x
关系式法:
能准确反映因变量与自变量的数值关系
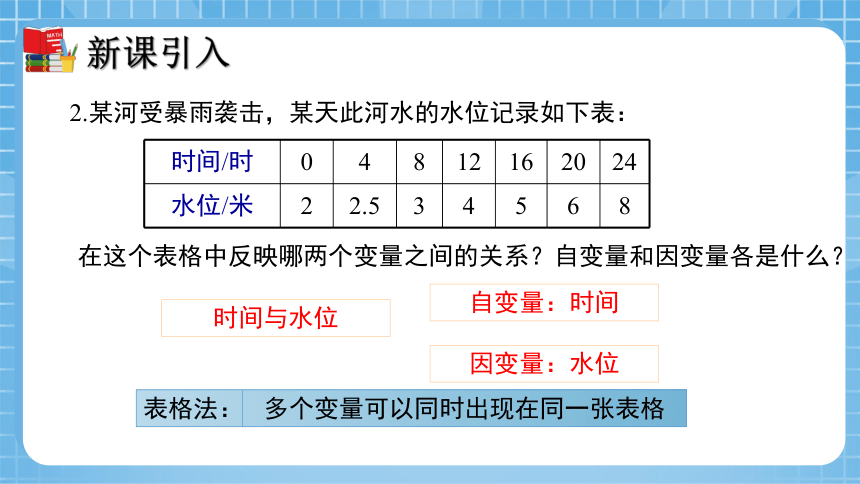
2.某河受暴雨袭击,某天此河水的水位记录如下表:
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
在这个表格中反映哪两个变量之间的关系?自变量和因变量各是什么?
时间与水位
自变量:时间
因变量:水位
表格法:
多个变量可以同时出现在同一张表格
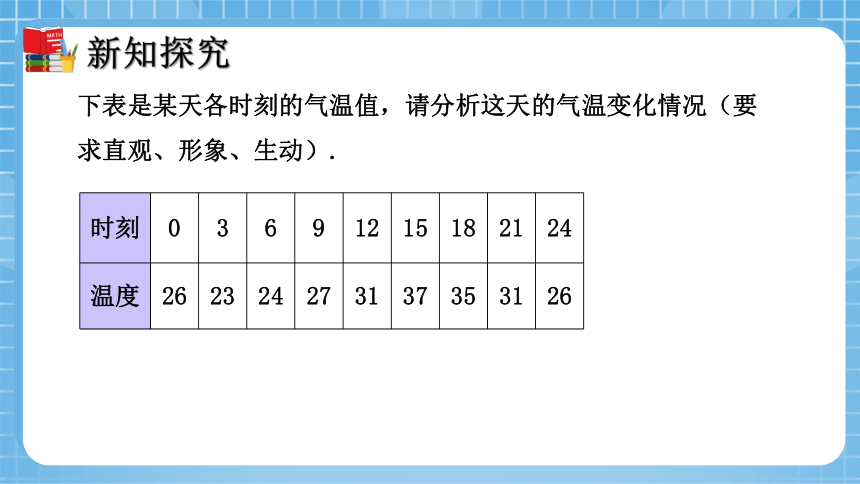
下表是某天各时刻的气温值,请分析这天的气温变化情况(要求直观、形象、生动).
时刻 0 3 6 9 12 15 18 21 24
温度 26 23 24 27 31 37 35 31 26
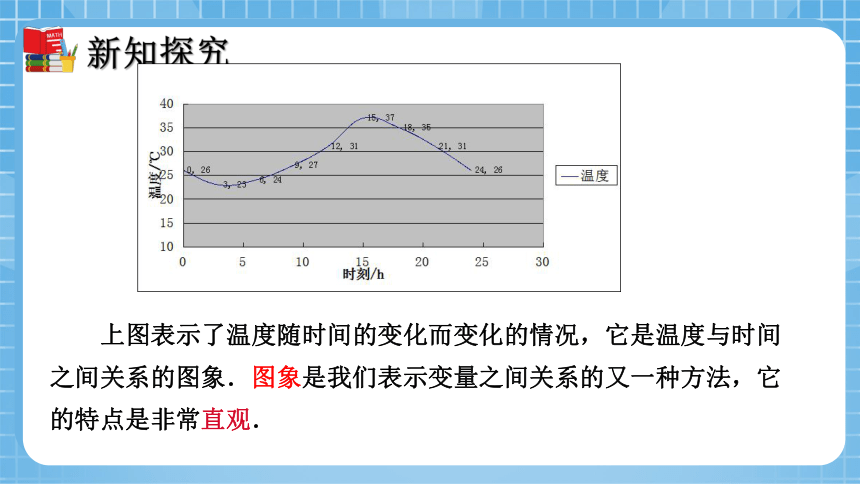
上图表示了温度随时间的变化而变化的情况,它是温度与时间之间关系的图象.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
温度/ C
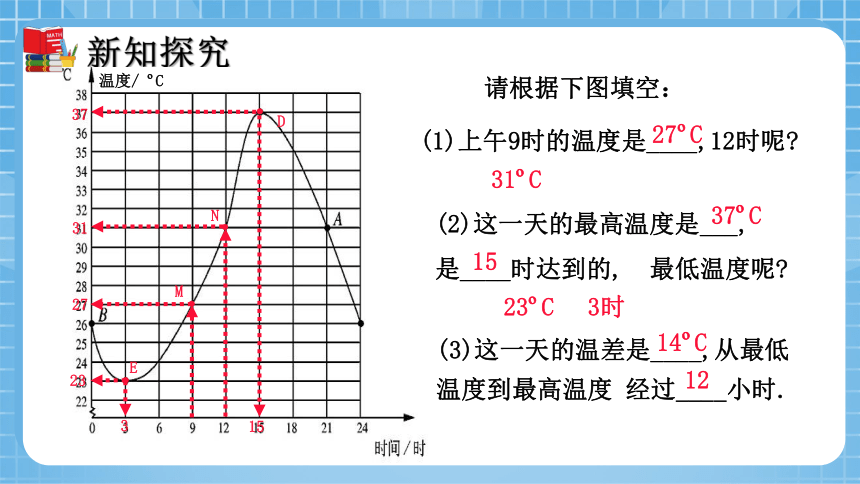
请根据下图填空:
(1)上午9时的温度是____,12时呢
(2)这一天的最高温度是___,
是____时达到的, 最低温度呢
(3)这一天的温差是____,从最低温度到最高温度 经过____小时.
27
31
14 C
M
D
N
27 C
31 C
37
15
E
37 C
15
23
23 C
3
3时
12
温度/ C
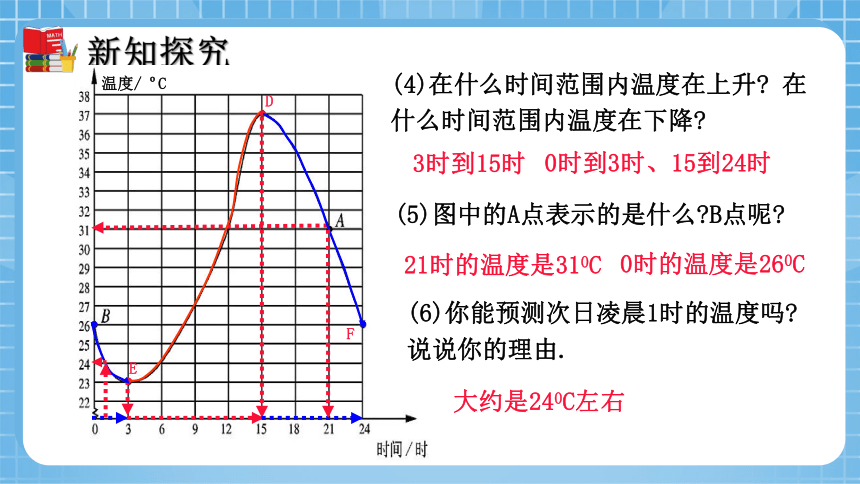
(4)在什么时间范围内温度在上升 在什么时间范围内温度在下降
(5)图中的A点表示的是什么 B点呢
(6)你能预测次日凌晨1时的温度吗 说说你的理由.
D
E
F
0时到3时、15到24时
21时的温度是310C
0时的温度是260C
大约是240C左右
3时到15时
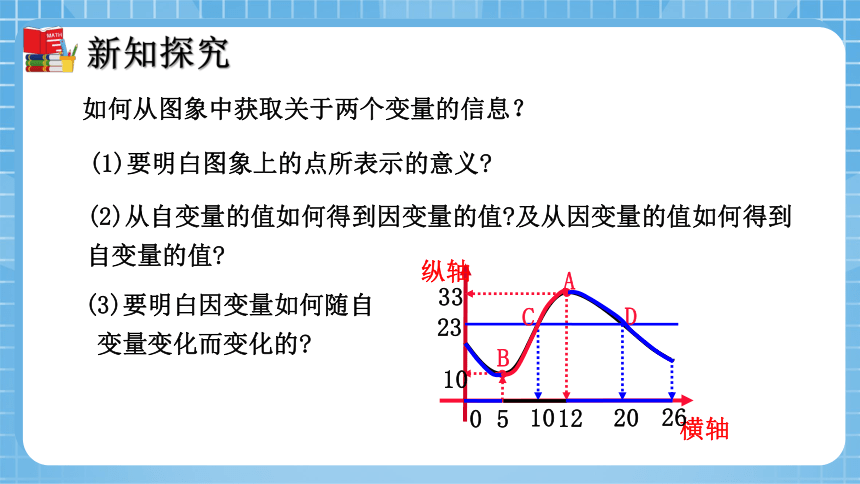
如何从图象中获取关于两个变量的信息?
(1)要明白图象上的点所表示的意义
(2)从自变量的值如何得到因变量的值 及从因变量的值如何得到自变量的值
(3)要明白因变量如何随自
变量变化而变化的
横轴
纵轴
A
B
12
26
5
33
10
C
D
20
10
23
0
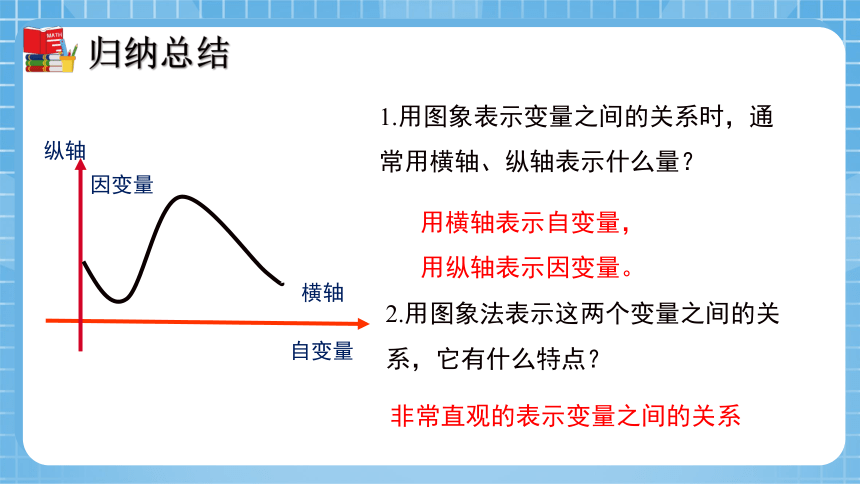
2.用图象法表示这两个变量之间的关系,它有什么特点?
1.用图象表示变量之间的关系时,通常用横轴、纵轴表示什么量?
用横轴表示自变量,用纵轴表示因变量。
非常直观的表示变量之间的关系
自变量
横轴
纵轴
因变量
3.要想了解图象上的点所表示的意义,做法是:
过点A做关于纵轴的平行线,
关于横轴的平行线。
横轴
纵轴
9
27
A
4.变化趋势:
上升线:表明因变量随自变量的
下降线:表示因变量随自变量的
水平线:表示因变量随自变量的
增大而增大
增大而减少
增大而不变
2
(1)大约什么时刻港口的水最深?约是多少?
(2)A点表示什么?
(3)说说这个港口从0时到6时的水位是怎样变化的?
0
1
1
2
3
4
8
7
6
5
水深(米)
时间(小时)
A
例1.下图表示了某港口某日从0时到6时水深变化的情况.
3
4
5
6
3时
7米
4时的水深
先上升,后下降
骆驼被称为“沙漠之舟” ,它的体温随时间的变化而发生较大的变化.
A
(1)一天中,骆驼的体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
0
4
8
12
16
20
24
28
32
36
40
44
48
33
35
37
39
41
温度/℃
时间/时
(图中25时表示次日凌晨1时)
35℃到40℃
12小时
(2)从16时到24时,骆驼的体温下降了多少?
3℃
0
4
8
12
16
20
24
28
32
36
40
44
48
33
35
37
39
41
温度/℃
时间/时
(图中25时表示次日凌晨1时)
(3)在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?
4时到16时、28时到40时
0时到4时、16时到28时、40时到48时
0
4
8
12
16
20
24
28
32
36
40
44
48
33
35
37
39
41
温度/℃
时间/时
(图中25时表示次日凌晨1时)
(4)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其他时刻呢?
每天同一时刻骆驼的体温都相同
(5)A点表示的是什么?还有几时的温度与A点所表示的温度相同?
A点表示12时骆驼的体温是39℃
20时、36时及44时的温度与A点所表示的温度相同.
(1)注意两数轴上的名称与单位
图象的识图技巧
(3)识图关键:弄清图象上点的意义,找准关键点:注意图象的起点、终点、最高点、最低点、拐点等特殊位置,并弄清这些点所表示的意义.
(2)分布规律:横轴上的点表示自变量,纵轴上的点表示因变量.
表示变量间的关系方法
横轴表示自变量,纵轴表示因变量
表格法
关系式
图象法
多个变量可以同时出现在同一张表格
图象上的点所表示的意义
图象上的变化趋势:上升线;水平线;下降线
能准确反映因变量与自变量的数值关系
例2.已知y与x的关系的图象如图所示,根据图象回答下列问题:
(1)确定自变量x的取值范围.
(2)当x=-4,-2,4时,y的值分别是多少?
(3)当y=0,4时,x的值分别是多少?
(4)当x取何值时,y的值最大?当x取何值时,y的值最小?
(5)当x的值在什么范围内时,y随x的增大而增大?当x的值
在什么范围内时,y随x的增大而减小?
解:(1)-4≤x≤4.
(2)y的值分别是2,-2,0.
(3)当y=0时,x的值是-3,-1或4;当y=4时,x的值是1.5.
(4)当x=1.5时,y的值最大;当x=-2时,y的值最小.
(5)当-2≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小.
1. 如图是某地区一天的气温随时间变化的图象,根据图象信息,下列说法正确的是( )
A. 气温T(℃)是自变量,时间t
(时)是因变量
B. 这一天最高气温是14 ℃
C. 4时至14时气温T(℃)随时间
t(时)的增大而增大
D. 24时气温最低
C
2.某市一周平均气温( ℃ )如图所示,下列说法不正确的是
( )
A.星期二的平均气温最高;
B.星期四到星期日天气逐渐转暖;
C.这一周最高气温与最低气温相差4 ℃;
D.星期四的平均气温最低
气温
o
1 2 3 4 5 6 7 星期
12
10
8
6
4
2
3.如图是北京市某一天的气温T(℃)随时间t(h)变化的图象,那么这天( )
A.最高气温是10℃,最低气温是0℃
B.最高气温是6℃,最低气温是-2℃
C.从5时到12时气温在逐渐升高
D.从12时到24时气温在逐渐升高
C
4.在夏天一杯开水放在桌面上,其水温T与放置时间 t 的关系大致图象为( )
o
T
t
o
T
t
o
T
t
o
T
t
A
B
C
D
5.海水受日月的引力而产生潮汐现象,早晨海水上涨叫作潮,黄昏海水上涨叫做汐,合称潮汐.潮汐与人类的生活有着密切的联系.下面是某港口从0时到12时的水深情况.
时间/时
水深/米
A
B
6. 某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是_________,因变量是_________;
(2)无人机在75米高的上空停留的时间是_________分钟;
(3)在上升或下降过程中,无人机的速度为_________米/分;
解:(1)横轴代表的是无人机被操控的时间,纵轴是无人机飞行的高度,所以自变量是操控无人机的时间;因变量是无人机的飞行高度h;
(2)无人机在75米高的上空停留时间为分钟;
(3)在上升或下降过程中,无人机的速度为:米/分;
7.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
【详解】(1)由图可得,自变量是t,因变量是s,
(2)由图可得,小明家到滨海公园的路程为30km,
小明在中心书城逗留的时间为2.5-0.8=1.7(h);
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
8.如图表示某市6月份某一天的气温随时间变化的情况,请观察此图回答下列问题:
(1)这天的最高气温 是 ;
(2)这天在 范围内温度在上升;
(3)请你预测一下,次日凌晨1点的气温大约是多少度?
38度
3至15时
25度
1.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
2.曲线型图象能够反映出数据的变化趋势,通过结合横纵坐标轴表示的意义,我们能够很直观的感受到数据的意义.
习题3.3
第1、2题
3.3 用图象表示的变量间关系
第1课时
学习目标
1)结合具体情境,能理解图象上的点所表示的意义。
2)能从图象中获取变量之间关系的信息,并对未来的情况进行预测。
重点
能够从曲线型图象中获取关于两个变量的信息。
难点
从已知图象中发现变量之间存在的关系,并能将图中的有用信息读取出来。
我们已经学习了几种表示变量之间关系的方法
变量之间关系的表示 特征
列表法 能看出两个变量之间的变化关系
关系式法 给定一个变量的值可求出另一个变量的值
1.“五一”黄金周中,若用x表示七天假期中已过的天数,y表示所剩天数,则y与x的关系式可表示为:
y =7-x
关系式法:
能准确反映因变量与自变量的数值关系
2.某河受暴雨袭击,某天此河水的水位记录如下表:
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
在这个表格中反映哪两个变量之间的关系?自变量和因变量各是什么?
时间与水位
自变量:时间
因变量:水位
表格法:
多个变量可以同时出现在同一张表格
下表是某天各时刻的气温值,请分析这天的气温变化情况(要求直观、形象、生动).
时刻 0 3 6 9 12 15 18 21 24
温度 26 23 24 27 31 37 35 31 26
上图表示了温度随时间的变化而变化的情况,它是温度与时间之间关系的图象.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
温度/ C
请根据下图填空:
(1)上午9时的温度是____,12时呢
(2)这一天的最高温度是___,
是____时达到的, 最低温度呢
(3)这一天的温差是____,从最低温度到最高温度 经过____小时.
27
31
14 C
M
D
N
27 C
31 C
37
15
E
37 C
15
23
23 C
3
3时
12
温度/ C
(4)在什么时间范围内温度在上升 在什么时间范围内温度在下降
(5)图中的A点表示的是什么 B点呢
(6)你能预测次日凌晨1时的温度吗 说说你的理由.
D
E
F
0时到3时、15到24时
21时的温度是310C
0时的温度是260C
大约是240C左右
3时到15时
如何从图象中获取关于两个变量的信息?
(1)要明白图象上的点所表示的意义
(2)从自变量的值如何得到因变量的值 及从因变量的值如何得到自变量的值
(3)要明白因变量如何随自
变量变化而变化的
横轴
纵轴
A
B
12
26
5
33
10
C
D
20
10
23
0
2.用图象法表示这两个变量之间的关系,它有什么特点?
1.用图象表示变量之间的关系时,通常用横轴、纵轴表示什么量?
用横轴表示自变量,用纵轴表示因变量。
非常直观的表示变量之间的关系
自变量
横轴
纵轴
因变量
3.要想了解图象上的点所表示的意义,做法是:
过点A做关于纵轴的平行线,
关于横轴的平行线。
横轴
纵轴
9
27
A
4.变化趋势:
上升线:表明因变量随自变量的
下降线:表示因变量随自变量的
水平线:表示因变量随自变量的
增大而增大
增大而减少
增大而不变
2
(1)大约什么时刻港口的水最深?约是多少?
(2)A点表示什么?
(3)说说这个港口从0时到6时的水位是怎样变化的?
0
1
1
2
3
4
8
7
6
5
水深(米)
时间(小时)
A
例1.下图表示了某港口某日从0时到6时水深变化的情况.
3
4
5
6
3时
7米
4时的水深
先上升,后下降
骆驼被称为“沙漠之舟” ,它的体温随时间的变化而发生较大的变化.
A
(1)一天中,骆驼的体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
0
4
8
12
16
20
24
28
32
36
40
44
48
33
35
37
39
41
温度/℃
时间/时
(图中25时表示次日凌晨1时)
35℃到40℃
12小时
(2)从16时到24时,骆驼的体温下降了多少?
3℃
0
4
8
12
16
20
24
28
32
36
40
44
48
33
35
37
39
41
温度/℃
时间/时
(图中25时表示次日凌晨1时)
(3)在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?
4时到16时、28时到40时
0时到4时、16时到28时、40时到48时
0
4
8
12
16
20
24
28
32
36
40
44
48
33
35
37
39
41
温度/℃
时间/时
(图中25时表示次日凌晨1时)
(4)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其他时刻呢?
每天同一时刻骆驼的体温都相同
(5)A点表示的是什么?还有几时的温度与A点所表示的温度相同?
A点表示12时骆驼的体温是39℃
20时、36时及44时的温度与A点所表示的温度相同.
(1)注意两数轴上的名称与单位
图象的识图技巧
(3)识图关键:弄清图象上点的意义,找准关键点:注意图象的起点、终点、最高点、最低点、拐点等特殊位置,并弄清这些点所表示的意义.
(2)分布规律:横轴上的点表示自变量,纵轴上的点表示因变量.
表示变量间的关系方法
横轴表示自变量,纵轴表示因变量
表格法
关系式
图象法
多个变量可以同时出现在同一张表格
图象上的点所表示的意义
图象上的变化趋势:上升线;水平线;下降线
能准确反映因变量与自变量的数值关系
例2.已知y与x的关系的图象如图所示,根据图象回答下列问题:
(1)确定自变量x的取值范围.
(2)当x=-4,-2,4时,y的值分别是多少?
(3)当y=0,4时,x的值分别是多少?
(4)当x取何值时,y的值最大?当x取何值时,y的值最小?
(5)当x的值在什么范围内时,y随x的增大而增大?当x的值
在什么范围内时,y随x的增大而减小?
解:(1)-4≤x≤4.
(2)y的值分别是2,-2,0.
(3)当y=0时,x的值是-3,-1或4;当y=4时,x的值是1.5.
(4)当x=1.5时,y的值最大;当x=-2时,y的值最小.
(5)当-2≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小.
1. 如图是某地区一天的气温随时间变化的图象,根据图象信息,下列说法正确的是( )
A. 气温T(℃)是自变量,时间t
(时)是因变量
B. 这一天最高气温是14 ℃
C. 4时至14时气温T(℃)随时间
t(时)的增大而增大
D. 24时气温最低
C
2.某市一周平均气温( ℃ )如图所示,下列说法不正确的是
( )
A.星期二的平均气温最高;
B.星期四到星期日天气逐渐转暖;
C.这一周最高气温与最低气温相差4 ℃;
D.星期四的平均气温最低
气温
o
1 2 3 4 5 6 7 星期
12
10
8
6
4
2
3.如图是北京市某一天的气温T(℃)随时间t(h)变化的图象,那么这天( )
A.最高气温是10℃,最低气温是0℃
B.最高气温是6℃,最低气温是-2℃
C.从5时到12时气温在逐渐升高
D.从12时到24时气温在逐渐升高
C
4.在夏天一杯开水放在桌面上,其水温T与放置时间 t 的关系大致图象为( )
o
T
t
o
T
t
o
T
t
o
T
t
A
B
C
D
5.海水受日月的引力而产生潮汐现象,早晨海水上涨叫作潮,黄昏海水上涨叫做汐,合称潮汐.潮汐与人类的生活有着密切的联系.下面是某港口从0时到12时的水深情况.
时间/时
水深/米
A
B
6. 某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是_________,因变量是_________;
(2)无人机在75米高的上空停留的时间是_________分钟;
(3)在上升或下降过程中,无人机的速度为_________米/分;
解:(1)横轴代表的是无人机被操控的时间,纵轴是无人机飞行的高度,所以自变量是操控无人机的时间;因变量是无人机的飞行高度h;
(2)无人机在75米高的上空停留时间为分钟;
(3)在上升或下降过程中,无人机的速度为:米/分;
7.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
【详解】(1)由图可得,自变量是t,因变量是s,
(2)由图可得,小明家到滨海公园的路程为30km,
小明在中心书城逗留的时间为2.5-0.8=1.7(h);
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
8.如图表示某市6月份某一天的气温随时间变化的情况,请观察此图回答下列问题:
(1)这天的最高气温 是 ;
(2)这天在 范围内温度在上升;
(3)请你预测一下,次日凌晨1点的气温大约是多少度?
38度
3至15时
25度
1.图象是我们表示变量之间关系的又一种方法,它的特点是非常直观.
2.曲线型图象能够反映出数据的变化趋势,通过结合横纵坐标轴表示的意义,我们能够很直观的感受到数据的意义.
习题3.3
第1、2题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
