北师大版数学七年级下册3.3 用图象表示的变量间关系(第2课时)同步课件
文档属性
| 名称 | 北师大版数学七年级下册3.3 用图象表示的变量间关系(第2课时)同步课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览








文档简介
3.3 用图象表示的变量间关系
第2课时
1.经历从图象中分析变量之间关系的过程,进一步体会变量之间的关系.
2.结合具体情境理解图象上的点所表示的意义.
3.能从图象中获取变量之间关系的信息,感受几何直观的作用,并能用语言进行描述.
1、上节课我们学了哪种方法来表示自变量与因变量之间的关系?
图象法,即用图象表示变量之间的关系的方法.
2、图象法表示变量之间的关系有什么特点?
它的特点是非常直观,通过结合横纵坐标轴表示的意义,我们能够很直观的感受到数据的意义.
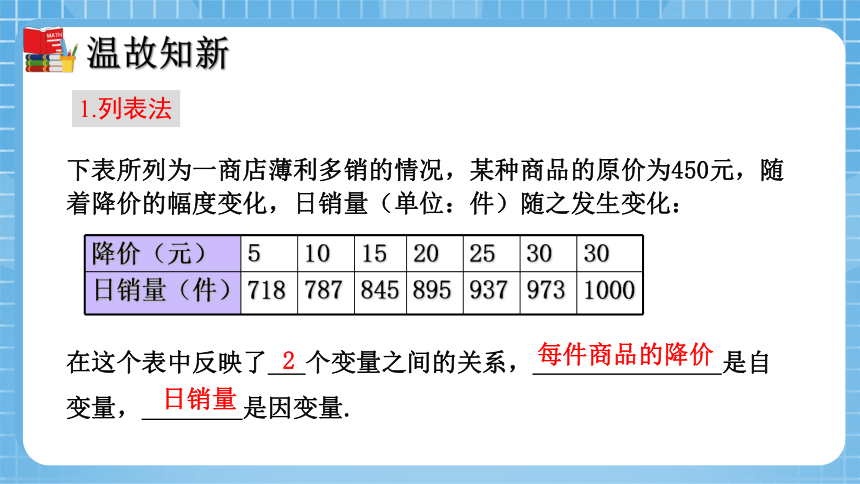
下表所列为一商店薄利多销的情况,某种商品的原价为450元,随着降价的幅度变化,日销量(单位:件)随之发生变化:
降价(元)
5
10
15
20
25
30
30
日销量(件)
718
787
845
895
937
973
1000
在这个表中反映了 个变量之间的关系, 是自变量, 是因变量.
2
每件商品的降价
日销量
1.列表法
某出租车每小时行驶60千米,若 t 小时行驶 S 千米,则自变量是__________,因变量是_____________,s 与 t 的关系式是_________.
行驶时间
行驶路程
S = 60t
2.关系式法
3.图象法(曲线型图象)
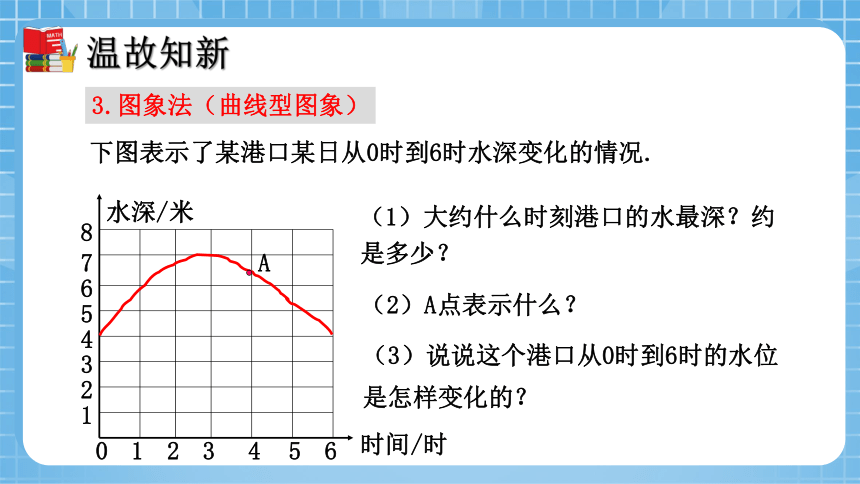
下图表示了某港口某日从0时到6时水深变化的情况.
(1)大约什么时刻港口的水最深?约是多少?
0
5
6
4
3
2
1
1
2
3
4
8
7
6
5
水深/米
时间/时
A
(2)A点表示什么?
(3)说说这个港口从0时到6时的水位是怎样变化的?
用折线型图象表示的变量间关系
每一辆汽车上都有一个时速表用来指示汽车当时的速度. 你知道现在汽车的速度是多少吗?
约为50km/h
下面三个图分别表示了汽车的速度v随时间t的变化情况,根据图象:
表示汽车是在匀速运动的是_____
表示汽车是在加速运动的是______
表示汽车是在减速运动的是______
A
B
C
t
t
v
v
v
o
o
o
A
B
C
t
汽车在行驶的过程中,速度往往是变化的,下面的图象表示一辆汽车的速度随时间变化而变化的情况.
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(km/h)
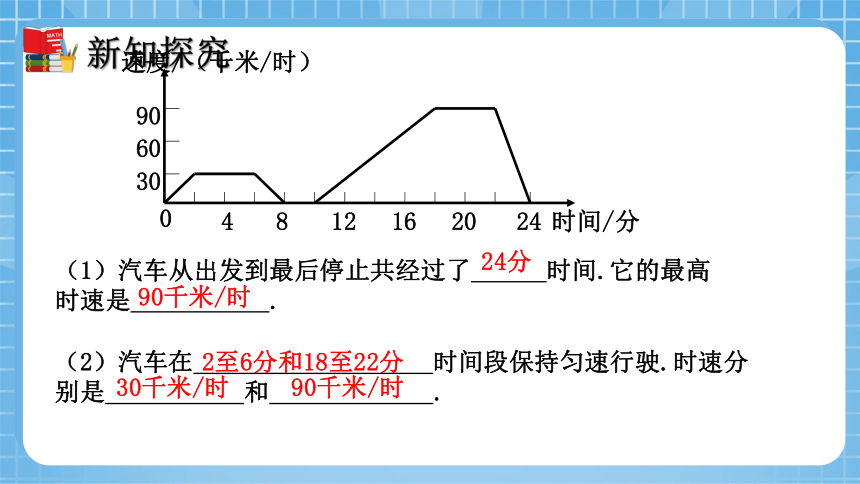
(1)汽车从出发到最后停止共经过了 时间.它的最高时速是 .
(2)汽车在 时间段保持匀速行驶.时速分别是 和 .
90千米/时
24分
2至6分和18至22分
30千米/时
90千米/时
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(千米/时)
(3)出发后8分到10分之间可能发生了什么情况?
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(km/h)
遇到红灯
(4)用自己的语言大致描述这辆汽车的行驶情况.
先加速行驶至30千米/小时,然后匀速行驶,再减速行驶至0千米/小时,然后停车休息2分钟,然后加速行驶至90千米/小时,然后匀速行驶,再减速行驶至0千米/小时
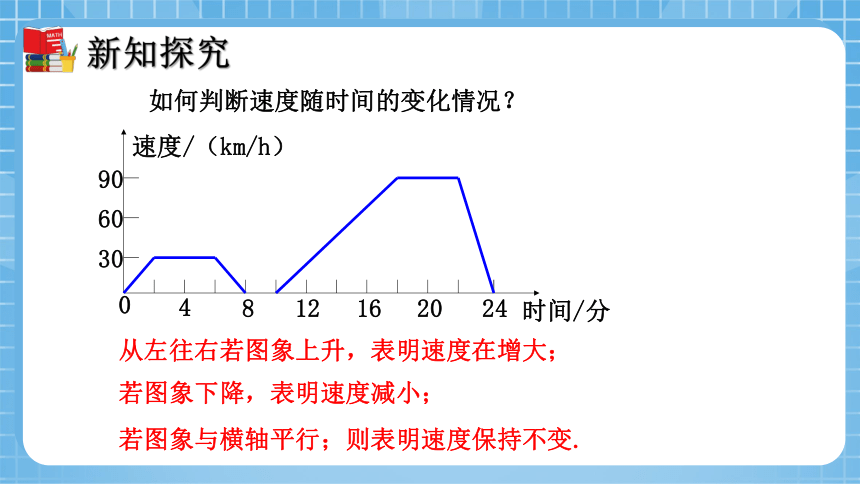
如何判断速度随时间的变化情况?
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(km/h)
从左往右若图象上升,表明速度在增大;
若图象下降,表明速度减小;
若图象与横轴平行;则表明速度保持不变.
根据图象读取信息时要注意:
(1)横轴和纵轴的意义.
(2)对于某个具体点,可向横、纵轴作垂线,从而求得具体的值;
(3)在实际问题中,要注意图象与横、纵轴的交点代表的实际意义.
在一个变化过程中,两个变量之间的关系,有时随着自变量的变化,因变量与自变量之间的关系也会发生变化,反映在图象上就是分段图象.
加速
速度v
时间t
速度v
时间t
减速
速度v
时间t
匀速
速度v
时间t
停止
速度v
时间t
减速
加速
0
0
0
0
0
变化速率相同
变化速率不同
速度v
时间t
0
探究速度随时间的变化
例1.一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶.汽车到达下一个车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下面的那一幅图可以近似地刻画出汽车在这段时间内的变化情况?
时间
时间
时间
速度
速度
0
时间
0
0
0
速度
速度
A
B
C
D
(B)
例2.某年初,我国西南部分省市遭遇了严重干旱.某水库的蓄水量随着时间的增加而减小,干旱持续时间 t(天)与蓄水量V(万立方米)的变化情况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)写出V和t之间的关系式?
干旱持续时间t/天
0
10
20
30
40
50
60
蓄水量V/万立方米
?
?
?
?
?
?
?
解:(2)填表如下:
(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)根据图象可知,该水库初始蓄水量为1 200万立方米,干旱每持续10天,蓄水量相应减少200万立方米,所以V和t之间的关系式为V=1 200- =-20t+1 200(0≤t≤60).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}干旱持续时间t/天2
0
10
20
30
40
50
60
蓄水量V/万立方米
1 200
1 000
800
600
400
200
0
做一做:星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方花了多少时间?离家多远?
(2)她何时开始第一次休息?休息了多
长时间?
解:观察图象可知:玲玲到离家最远的地方花了3小时,此时离家30千米;
10点半时开始第一次休息,休息了半小时;
(3)她骑车速度最快是在什么时候?车速是多少?
解:玲玲郊游过程中,
9时~10时,速度为1010?9=10(千米/时);
10时~10时30分,速度约为17.5?1010.5?10=15(千米/时);
10时30分~11时,速度为0;
11时~12时,速度为30?17.512?11=12.5(千米/时);
12时~13时,速度为0;
13时~15时,速度为3015?13=15(千米/时);
可见骑行最快有两段时间:10时~10时30分;13时~15时.两段时间的速度都是15千米/时.
?
(4)玲玲全程骑车的平均速度是多少?
1.李明骑车上学,一开始以某一速度行进,途中车子发生故障,只好停下来修车,车修好后,因怕耽误上学时间,于是加快马加鞭车速,在下图中给出的示意图中(s为距离,t为时间)符合以上情况的是 ( )
O
B
s
t
O
A
s
t
O
D
s
t
O
C
s
t
D
2. 如图.
(1)小明离开家去图书
馆每小时行驶________km,
用了________min;
(2)他在图书馆用去________min;
(3)小明从图书馆返回家中的速度是每小时________km,用了________min.
8
30
60
12
20
3.如图,折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )
A.4:00气温最低 B.6:00气温为24 ℃
C.14:00气温最高 D.气温是30 ℃的时刻为16:00
4. 小华骑电动车从家出发去西安交大,当他骑了一段路时,想起要买一本书,于是原路返回刚经过的新华书店,买到书后继续前往交大,如图3-25-5是他离家的距离
与时间的关系示意图,
请根据图中提供的信
息回答下列问题:
(1)小华家离西安交大的距离是多少?
(2)买到书后,小华从新华书店去西安交大骑车的平均速度是多少?
(3)本次去西安交大途中,小华一共行驶了多少米?
解:(1)根据图象可知,小华家离西安交大的距离是4 800 m.
(2)小华从新华书店去西安交大骑车的平均速度为(4 800-3 000)÷(28-24)=450(m/min).
(3)根据图象,小华一共行驶了4 000+(4 000-3 000)+(4 800-3 000)=6 800(m).
5.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的图象如图所示,请你根据图象,回答下列问题:
(1)这次龙舟赛的全程是多少米?哪队先到达终点?
(2)求乙与甲相遇时乙的速度.
1.一些变量之间的关系可以用图象法来表示。它形象、直观,便于探索趋势。
2.学会分析图象,要从图象中获得信息并有条理地用语言表达出来。
3.在观察图象时要注意它两轴上的名称与单位。
习题3.4
第3、4题
第2课时
1.经历从图象中分析变量之间关系的过程,进一步体会变量之间的关系.
2.结合具体情境理解图象上的点所表示的意义.
3.能从图象中获取变量之间关系的信息,感受几何直观的作用,并能用语言进行描述.
1、上节课我们学了哪种方法来表示自变量与因变量之间的关系?
图象法,即用图象表示变量之间的关系的方法.
2、图象法表示变量之间的关系有什么特点?
它的特点是非常直观,通过结合横纵坐标轴表示的意义,我们能够很直观的感受到数据的意义.
下表所列为一商店薄利多销的情况,某种商品的原价为450元,随着降价的幅度变化,日销量(单位:件)随之发生变化:
降价(元)
5
10
15
20
25
30
30
日销量(件)
718
787
845
895
937
973
1000
在这个表中反映了 个变量之间的关系, 是自变量, 是因变量.
2
每件商品的降价
日销量
1.列表法
某出租车每小时行驶60千米,若 t 小时行驶 S 千米,则自变量是__________,因变量是_____________,s 与 t 的关系式是_________.
行驶时间
行驶路程
S = 60t
2.关系式法
3.图象法(曲线型图象)
下图表示了某港口某日从0时到6时水深变化的情况.
(1)大约什么时刻港口的水最深?约是多少?
0
5
6
4
3
2
1
1
2
3
4
8
7
6
5
水深/米
时间/时
A
(2)A点表示什么?
(3)说说这个港口从0时到6时的水位是怎样变化的?
用折线型图象表示的变量间关系
每一辆汽车上都有一个时速表用来指示汽车当时的速度. 你知道现在汽车的速度是多少吗?
约为50km/h
下面三个图分别表示了汽车的速度v随时间t的变化情况,根据图象:
表示汽车是在匀速运动的是_____
表示汽车是在加速运动的是______
表示汽车是在减速运动的是______
A
B
C
t
t
v
v
v
o
o
o
A
B
C
t
汽车在行驶的过程中,速度往往是变化的,下面的图象表示一辆汽车的速度随时间变化而变化的情况.
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(km/h)
(1)汽车从出发到最后停止共经过了 时间.它的最高时速是 .
(2)汽车在 时间段保持匀速行驶.时速分别是 和 .
90千米/时
24分
2至6分和18至22分
30千米/时
90千米/时
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(千米/时)
(3)出发后8分到10分之间可能发生了什么情况?
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(km/h)
遇到红灯
(4)用自己的语言大致描述这辆汽车的行驶情况.
先加速行驶至30千米/小时,然后匀速行驶,再减速行驶至0千米/小时,然后停车休息2分钟,然后加速行驶至90千米/小时,然后匀速行驶,再减速行驶至0千米/小时
如何判断速度随时间的变化情况?
0
4
8
12
16
20
24
90
60
30
时间/分
速度/(km/h)
从左往右若图象上升,表明速度在增大;
若图象下降,表明速度减小;
若图象与横轴平行;则表明速度保持不变.
根据图象读取信息时要注意:
(1)横轴和纵轴的意义.
(2)对于某个具体点,可向横、纵轴作垂线,从而求得具体的值;
(3)在实际问题中,要注意图象与横、纵轴的交点代表的实际意义.
在一个变化过程中,两个变量之间的关系,有时随着自变量的变化,因变量与自变量之间的关系也会发生变化,反映在图象上就是分段图象.
加速
速度v
时间t
速度v
时间t
减速
速度v
时间t
匀速
速度v
时间t
停止
速度v
时间t
减速
加速
0
0
0
0
0
变化速率相同
变化速率不同
速度v
时间t
0
探究速度随时间的变化
例1.一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶.汽车到达下一个车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下面的那一幅图可以近似地刻画出汽车在这段时间内的变化情况?
时间
时间
时间
速度
速度
0
时间
0
0
0
速度
速度
A
B
C
D
(B)
例2.某年初,我国西南部分省市遭遇了严重干旱.某水库的蓄水量随着时间的增加而减小,干旱持续时间 t(天)与蓄水量V(万立方米)的变化情况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)写出V和t之间的关系式?
干旱持续时间t/天
0
10
20
30
40
50
60
蓄水量V/万立方米
?
?
?
?
?
?
?
解:(2)填表如下:
(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)根据图象可知,该水库初始蓄水量为1 200万立方米,干旱每持续10天,蓄水量相应减少200万立方米,所以V和t之间的关系式为V=1 200- =-20t+1 200(0≤t≤60).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}干旱持续时间t/天2
0
10
20
30
40
50
60
蓄水量V/万立方米
1 200
1 000
800
600
400
200
0
做一做:星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方花了多少时间?离家多远?
(2)她何时开始第一次休息?休息了多
长时间?
解:观察图象可知:玲玲到离家最远的地方花了3小时,此时离家30千米;
10点半时开始第一次休息,休息了半小时;
(3)她骑车速度最快是在什么时候?车速是多少?
解:玲玲郊游过程中,
9时~10时,速度为1010?9=10(千米/时);
10时~10时30分,速度约为17.5?1010.5?10=15(千米/时);
10时30分~11时,速度为0;
11时~12时,速度为30?17.512?11=12.5(千米/时);
12时~13时,速度为0;
13时~15时,速度为3015?13=15(千米/时);
可见骑行最快有两段时间:10时~10时30分;13时~15时.两段时间的速度都是15千米/时.
?
(4)玲玲全程骑车的平均速度是多少?
1.李明骑车上学,一开始以某一速度行进,途中车子发生故障,只好停下来修车,车修好后,因怕耽误上学时间,于是加快马加鞭车速,在下图中给出的示意图中(s为距离,t为时间)符合以上情况的是 ( )
O
B
s
t
O
A
s
t
O
D
s
t
O
C
s
t
D
2. 如图.
(1)小明离开家去图书
馆每小时行驶________km,
用了________min;
(2)他在图书馆用去________min;
(3)小明从图书馆返回家中的速度是每小时________km,用了________min.
8
30
60
12
20
3.如图,折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )
A.4:00气温最低 B.6:00气温为24 ℃
C.14:00气温最高 D.气温是30 ℃的时刻为16:00
4. 小华骑电动车从家出发去西安交大,当他骑了一段路时,想起要买一本书,于是原路返回刚经过的新华书店,买到书后继续前往交大,如图3-25-5是他离家的距离
与时间的关系示意图,
请根据图中提供的信
息回答下列问题:
(1)小华家离西安交大的距离是多少?
(2)买到书后,小华从新华书店去西安交大骑车的平均速度是多少?
(3)本次去西安交大途中,小华一共行驶了多少米?
解:(1)根据图象可知,小华家离西安交大的距离是4 800 m.
(2)小华从新华书店去西安交大骑车的平均速度为(4 800-3 000)÷(28-24)=450(m/min).
(3)根据图象,小华一共行驶了4 000+(4 000-3 000)+(4 800-3 000)=6 800(m).
5.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的图象如图所示,请你根据图象,回答下列问题:
(1)这次龙舟赛的全程是多少米?哪队先到达终点?
(2)求乙与甲相遇时乙的速度.
1.一些变量之间的关系可以用图象法来表示。它形象、直观,便于探索趋势。
2.学会分析图象,要从图象中获得信息并有条理地用语言表达出来。
3.在观察图象时要注意它两轴上的名称与单位。
习题3.4
第3、4题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
