24.1.1《圆》

(共34张PPT)
圆是生活中常见的图形，许多物体都给我们以圆的形象.
奥运五环
福建土楼
城市立体交通
天安门广场国庆花坛
平面设计图案中的“圆”
一切平面图形中，最美的是圆！
——毕达哥拉斯[古希腊数学家]
第23章 圆
学习目标：
１、理解并掌握圆的概念。
２、了解和认识圆的相关概念。
３、探究圆的一些基本特征。
４、能利用圆的概念及其特征解决一些实际问题。
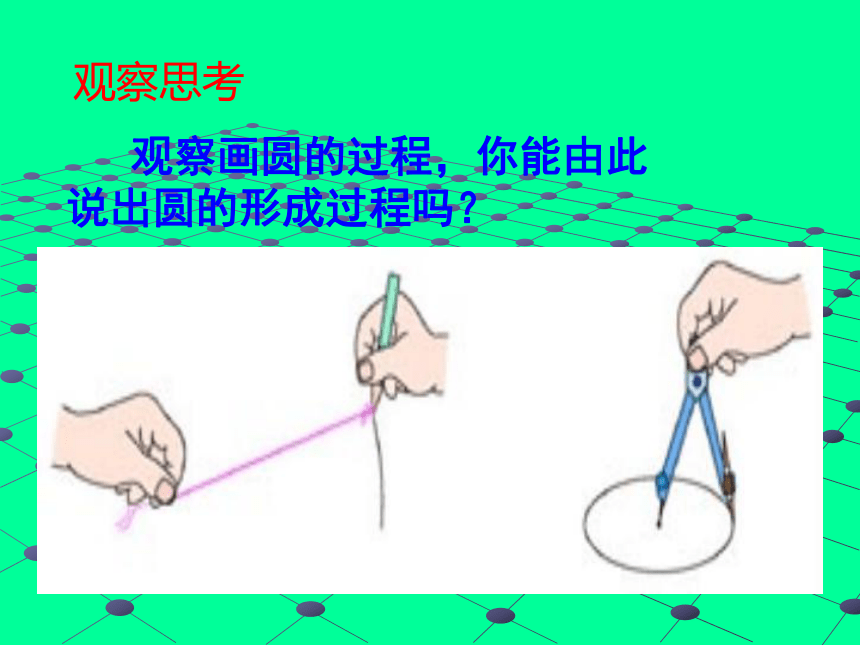
观察思考
观察画圆的过程，你能由此说出圆的形成过程吗？
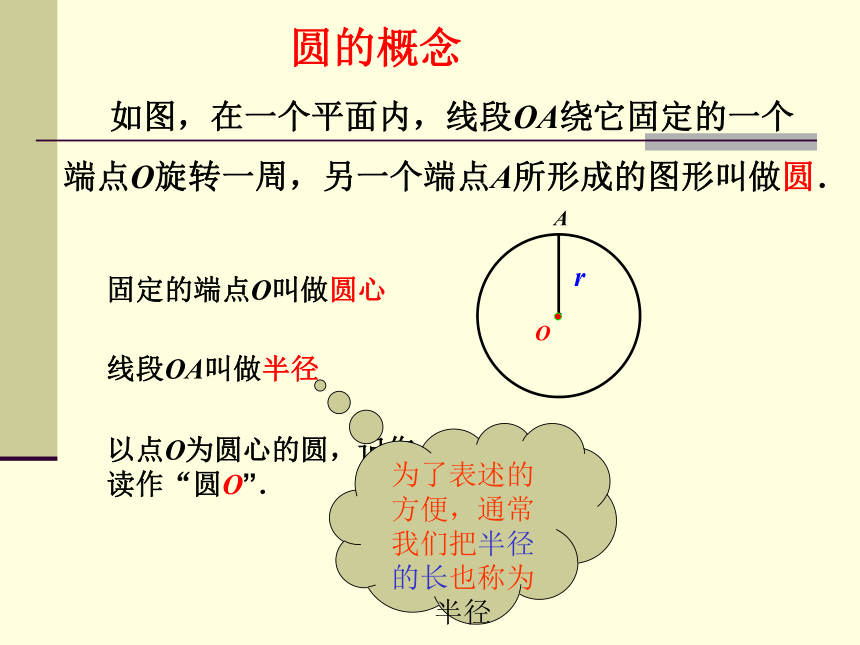
如图，在一个平面内，线段OA绕它固定的一个
端点O旋转一周，另一个端点A所形成的图形叫做圆．
·
r
O
A
固定的端点O叫做圆心
线段OA叫做半径
以点O为圆心的圆，记作“⊙O”，读作“圆O”．
圆的概念
为了表述的方便，通常我们把半径的长也称为半径
１、足球、太阳是圆吗？
观察画圆过程，思考并回答：
2、在你所画的圆上任意找几个点，用尺子量一量这几点到圆心的距离，看看有什么特点？
3、想一想，平面内到点O的距离等于线段OA的长的点都在同一个圆上吗？
我国古人很早对圆就有这样的认识了，战国时的《墨经》就有“圆，一中同长也”的记载．它的意思是圆上各点到圆心的距离都等于半径．
观察思考
观察画圆的过程，你能由此说出圆的形成过程吗？
归纳：
（1）圆上各点到定点 （圆心）的距离都等于 。
定长（半径r)
（2）平面内到定点的距离等于定长的点都在 。
同一个圆上
圆的第二种定义：
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合。
实践探索
1、以1厘米为半径能画几个圆？这些圆的位置和大小有什么特点？
大小相同（半径相同），位置不同（圆心不同），
2、以点O为圆心能画几个圆？这些圆的位置和大小有什么特点？
圆心相同，但圆的大小不同（半径不同），
这样的两个圆叫做等圆
这样的两个圆叫做同心圆。
●
要确定一个圆,必须确定圆的____和____
圆心
半径
圆心确定圆的位置,半径确定圆的大小.
O
根据圆的定义，“圆”指的是“ 圆周 ”，而不是“圆面”。
车轮为什么做成圆形
体验生活
经过圆心的弦（如图中的AB）叫做直径．
·
C
O
A
B
连接圆上任意两点的线段（如图AC）叫做弦，
与圆有关的概念
弦
活动& 探索

C
B
O
A
F
E
D
M
问：
（1）FC是弦吗？为什么？
（2）CM是弦吗？为什么？
（3）从图中你能找到哪些弦？
●
O
B
C
A
1.如图,半径有:____________
OA、OB、OC
△AOB是_____三角形.
2.如图,弦有:______________
AB、BC
AC
我们可以发现，在圆中有长度不等的弦，那么在一个圆中有没有最长的弦呢？
等边
等腰
若∠AOB=60°，则
课后小议
小明和小强为了探究 中有没有最长的弦，经过了大量的测量，最后得出一致结论，直径是圆中最长的弦，你认为他们的结论对吗？试说说你的理由.
⊙O
圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
·
C
O
A
B
弧
圆上任意两点间的部分叫做圆弧，简称弧．以A、B为端点的弧记作 ，读作“圆弧AB”或“弧AB”．
·
C
O
A
B
劣弧与优弧
小于半圆的弧（如图中的　　　　）叫做劣弧；
大于半圆的弧（用三个字母表示，如图中的 ）叫做优弧.
●
O
B
C
A
1.如图,弧有:______________
⌒
AB
⌒
BC
⌒
ABC
⌒
ACB
⌒
BAC
它们一样么？
⌒
AB
⌒
BC
2 .劣弧有：
优弧有：
⌒
ACB
⌒
BAC
你知道优弧与劣弧的区别么？
如图，请正确的方式表示出以点A为端点的优弧及劣弧.
1.如何在操场上画一个半径是5m的圆？说出你的理由
首先确定圆心, 然后用5米长的绳子一端固定为圆心端,另一端系在一端尖木棒,木棒以5米长尖端划动一周,所形成的图形就是所画的圆.
根据圆的形成定义
判断正误:
(1)弦是直径；
(2)半圆是弧；
(3)过圆心的线段是直径；
(7)圆心相同，半径相等的两个圆是同心圆;
(8)半径相等的两个圆是等圆.
(4)过圆心的直线是直径；
(5)半圆是最长的弧；
(6)直径是最长的弦；
2 你见过树木的年轮吗 从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径每年增加多少 .
解:
23÷2÷20=0.575（cm ）
答: 这棵红衫树的半径每年增加0.575cm
想一想：
本节课你有什么收获？
有什么困惑？