11.3 图形的中心对称(1)课件 (共14张PPT)青岛版数学八年级下册
文档属性
| 名称 | 11.3 图形的中心对称(1)课件 (共14张PPT)青岛版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
第十一章 图形的平移与旋转
11.3 图形的中心对称
第1课时
1.了解中心对称、两个图形成中心对称的概念;
2.掌握中心对称的基本性质,并会作与已知图形成中心对称的图形.
任务一:了解中心对称、两个图形成中心对称的概念及性质.
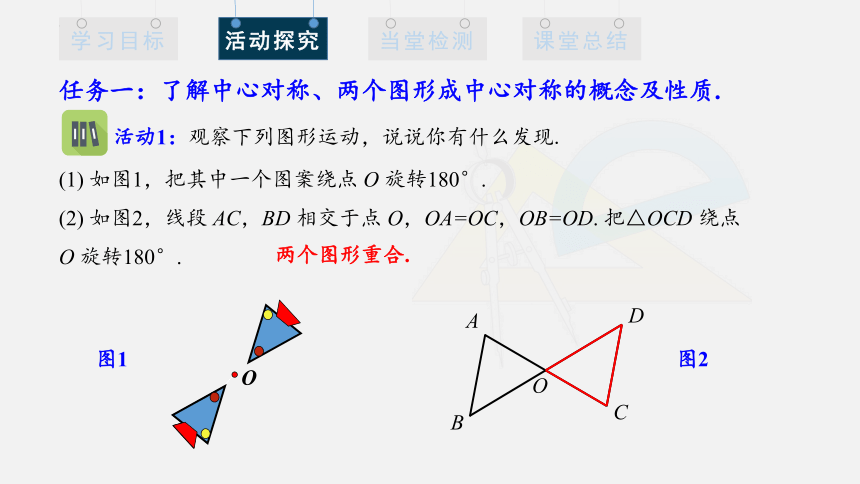
活动1:观察下列图形运动,说说你有什么发现.
O
A
B
D
C
O
两个图形重合.
(1) 如图1,把其中一个图案绕点 O 旋转180°.
(2) 如图2,线段 AC,BD 相交于点 O,OA=OC,OB=OD. 把△OCD 绕点O 旋转180°.
图1
图2
在平面内将一个图形绕某一定点旋转180°,图形的这种变化叫做中心对称,这个定点叫做对称中心.一个图形经过中心对称能与另一个图形重合,
就说这两个图形关于这个定点成中心对称.
中心对称是旋转变换的特殊情况,
成中心对称的两个图形是全等形.
活动小结
A′
A
B
C
C′
B′
O
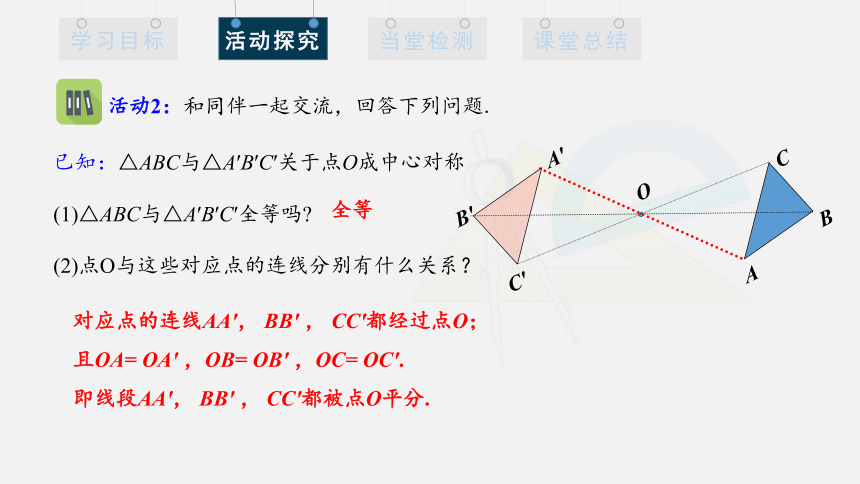
已知:△ABC与△A′B′C′关于点O成中心对称
(1)△ABC与△A′B′C′全等吗
(2)点O与这些对应点的连线分别有什么关系?
活动2:和同伴一起交流,回答下列问题.
对应点的连线AA′, BB′ , CC′都经过点O;且OA= OA′ ,OB= OB′ ,OC= OC′.
即线段AA′, BB′ , CC′都被点O平分.
全等
活动小结
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
中心对称的性质:
练一练
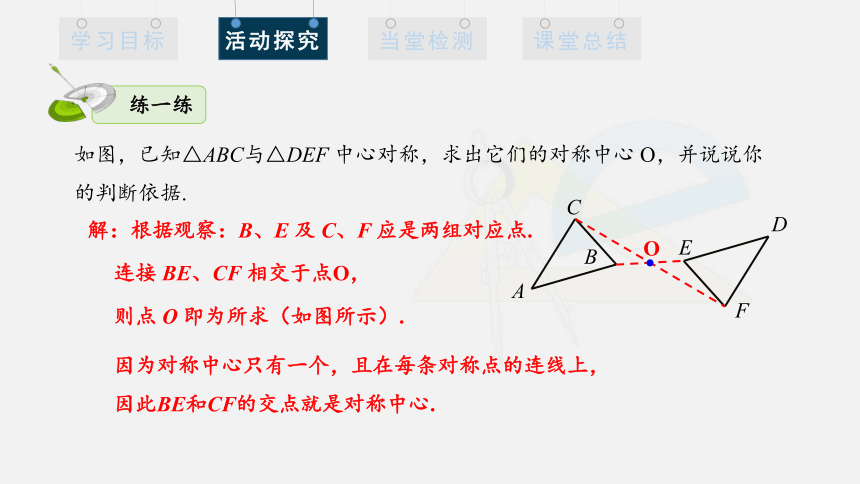
如图,已知△ABC与△DEF 中心对称,求出它们的对称中心 O,并说说你的判断依据.
A
B
C
D
E
F
O
解:根据观察:B、E 及 C、F 应是两组对应点.
连接 BE、CF 相交于点O,
则点 O 即为所求(如图所示).
因为对称中心只有一个,且在每条对称点的连线上,因此BE和CF的交点就是对称中心.
活动:如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对称点,再顺次连接各对应点即可.
A
B
C
D
O
任务二:作与已知图形成中心对称的图形.
(2)同理,可作出点B,C,D的对应点B',C',D';
(3)顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
A
B
C
D
O
A'
B'
C'
D'
作法:(1)连接AO并延长到A',使OA'=OA,得到点A的对应点A';
如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
活动小结
中心对称作图的一般步骤:
(1)确定出对称中心;
(2)确定出原图形的关键点(如三角形的顶点、图形的拐点等);
(3)作出这些关键点关于对称中心的对应点;
(4)顺次连接各对应点,即可得到所要画的图形.
1.下列说法正确的是( )
A.全等的两个图形成中心对称
B.能够完全重合的两个图形成中心对称
C.绕某点旋转后能重合的两个图形成中心对称
D.绕某点旋转180°后能够重合的两个图形成中心对称
D
2.如图,已知四边形ABCD和中心对称点O (O点为BC边的中点),请画出与它成中心对称的图形.
M
D
A
B
C
O
.
N
3.在直角坐标系中,已知点A(4,0),B(0,-3),C(2,1),D(-1,2),E(-4,-3). 分别作出它们关于原点O成中心对称的点,并写出对称点的坐标.由此你发现关于原点成中心对称的两个点的坐标有什么关系.
A′(-4,0),B′(0,3),C′(-2,-1),D′(1,-2),E′(4,3).
A′
B′
C′
D′
E′
关系:点P(x,y)关于原点O的
对称点为P′(-x,-y).
针对本课关键词“中心对称”,说说你学到了什么?
概念
性质
作图
中心对称
第十一章 图形的平移与旋转
11.3 图形的中心对称
第1课时
1.了解中心对称、两个图形成中心对称的概念;
2.掌握中心对称的基本性质,并会作与已知图形成中心对称的图形.
任务一:了解中心对称、两个图形成中心对称的概念及性质.
活动1:观察下列图形运动,说说你有什么发现.
O
A
B
D
C
O
两个图形重合.
(1) 如图1,把其中一个图案绕点 O 旋转180°.
(2) 如图2,线段 AC,BD 相交于点 O,OA=OC,OB=OD. 把△OCD 绕点O 旋转180°.
图1
图2
在平面内将一个图形绕某一定点旋转180°,图形的这种变化叫做中心对称,这个定点叫做对称中心.一个图形经过中心对称能与另一个图形重合,
就说这两个图形关于这个定点成中心对称.
中心对称是旋转变换的特殊情况,
成中心对称的两个图形是全等形.
活动小结
A′
A
B
C
C′
B′
O
已知:△ABC与△A′B′C′关于点O成中心对称
(1)△ABC与△A′B′C′全等吗
(2)点O与这些对应点的连线分别有什么关系?
活动2:和同伴一起交流,回答下列问题.
对应点的连线AA′, BB′ , CC′都经过点O;且OA= OA′ ,OB= OB′ ,OC= OC′.
即线段AA′, BB′ , CC′都被点O平分.
全等
活动小结
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
中心对称的性质:
练一练
如图,已知△ABC与△DEF 中心对称,求出它们的对称中心 O,并说说你的判断依据.
A
B
C
D
E
F
O
解:根据观察:B、E 及 C、F 应是两组对应点.
连接 BE、CF 相交于点O,
则点 O 即为所求(如图所示).
因为对称中心只有一个,且在每条对称点的连线上,因此BE和CF的交点就是对称中心.
活动:如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对称点,再顺次连接各对应点即可.
A
B
C
D
O
任务二:作与已知图形成中心对称的图形.
(2)同理,可作出点B,C,D的对应点B',C',D';
(3)顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
A
B
C
D
O
A'
B'
C'
D'
作法:(1)连接AO并延长到A',使OA'=OA,得到点A的对应点A';
如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
活动小结
中心对称作图的一般步骤:
(1)确定出对称中心;
(2)确定出原图形的关键点(如三角形的顶点、图形的拐点等);
(3)作出这些关键点关于对称中心的对应点;
(4)顺次连接各对应点,即可得到所要画的图形.
1.下列说法正确的是( )
A.全等的两个图形成中心对称
B.能够完全重合的两个图形成中心对称
C.绕某点旋转后能重合的两个图形成中心对称
D.绕某点旋转180°后能够重合的两个图形成中心对称
D
2.如图,已知四边形ABCD和中心对称点O (O点为BC边的中点),请画出与它成中心对称的图形.
M
D
A
B
C
O
.
N
3.在直角坐标系中,已知点A(4,0),B(0,-3),C(2,1),D(-1,2),E(-4,-3). 分别作出它们关于原点O成中心对称的点,并写出对称点的坐标.由此你发现关于原点成中心对称的两个点的坐标有什么关系.
A′(-4,0),B′(0,3),C′(-2,-1),D′(1,-2),E′(4,3).
A′
B′
C′
D′
E′
关系:点P(x,y)关于原点O的
对称点为P′(-x,-y).
针对本课关键词“中心对称”,说说你学到了什么?
概念
性质
作图
中心对称
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
