湘教版·2014-2015学年八年级数学下册精品课件:1.4角平分线的性质(共26张PPT)
文档属性
| 名称 | 湘教版·2014-2015学年八年级数学下册精品课件:1.4角平分线的性质(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 524.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-15 00:00:00 | ||
图片预览







文档简介
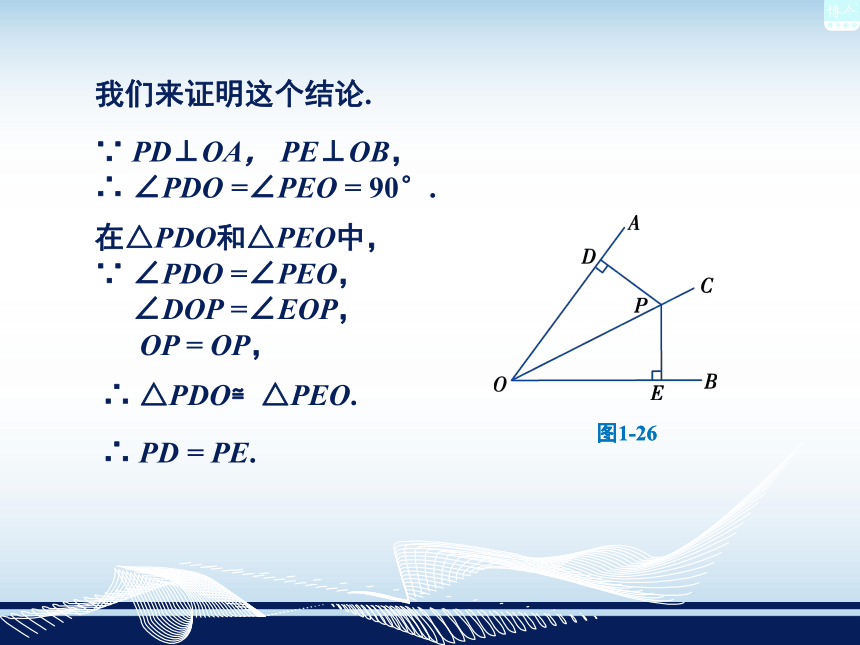
课件26张PPT。角平分线的性质1.4 角平分线是以一个角的顶点为端点的一条射线,它把这个角分成两个相等的角.图1-26∵ PD⊥OA, PE⊥OB,
∴ ∠PDO =∠PEO = 90°.在△PDO和△PEO中,
∵ ∠PDO =∠PEO,
∠DOP =∠EOP,
OP = OP,∴ △PDO≌△PEO.∴ PD = PE.我们来证明这个结论.图1-26图1-26角的平分线上的点到角的两边的距离相等.
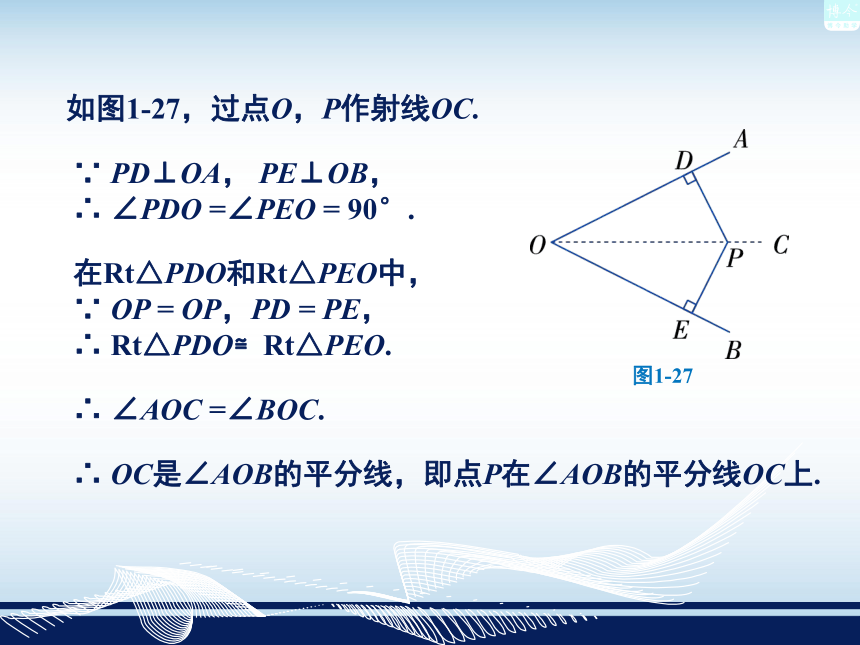
由此得到角平分线的性质定理:在Rt△PDO和Rt△PEO中,
∵ OP = OP,PD = PE,
∴ Rt△PDO≌Rt△PEO.∵ PD⊥OA, PE⊥OB,
∴ ∠PDO =∠PEO = 90°.如图1-27,过点O,P作射线OC.∴ ∠AOC =∠BOC.∴ OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.角的内部到角的两边距离相等的点在角的平分线上.
由此得到角平分线的性质定理的逆定理:又 BA⊥AD, BC⊥CD,∴ 点B在∠ADC的平分线上.(1)求证:点B在∠ADC的平分线上;图1-28证明: 在Rt△BAD和Rt△BCD中,
∵ BA = BC, BD = BD,∴ Rt△BAD≌Rt△BCD.∴ ∠ABD =∠CBD.∴ BD是∠ABC的平分线.(2)求证:BD是∠ABC的平分线.
解 作∠AOB的角平分线,交MN于一点,则这点即为所
求作的点P.(提示:用尺规作图)如图,在直线MN上求作一点P ,使点P到∠AOB两边
的距离相等.P2. 如图,在△ABC 中,AD 平分∠BAC, DE⊥AB
于点E,DF⊥AC 于点F,BD=CD.
求证:AB=AC. 如图1-29, 已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF 的中点. 需添加一个什么条件, 就可使CM,AM
分别为∠ACD和∠CAB的平分线呢?图1-29图1-29∵ ME⊥CD, MN⊥CA,同理可得AM是∠CAB的平分线.可以添加条件MN =ME (或MN =MF).∴ M在∠ACD的平分线上,即CM是∠ACD的平分线.图1-29∴ PE=PF.在△EBP中,BE+PE>PB,∴ BE+PF>PB.图1-30 如图1-31,你能在△ABC 中找到一点P,使其
到三边的距离相等吗?图1-31如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.2. 如图,在△ABC 中,AD⊥DE,BE⊥DE,AC,
BC 分别平分∠BAD,∠ABE,点C在线段DE上.
求证:AB=AD+BE.M证明 作CM⊥AB于点M. 1. 直角三角形的两个锐角有什么关系?
2. 直角三角形斜边上的中线与斜边有什么关系?
3. 请用自己的语言叙述勾股定理及其逆定理.
4. 判断两个直角三角形全等的方法有哪些?
5. 角平分线有哪些性质?
直角三角形斜边上的中线等于斜边的一半有两个角互余的三角形是直角三角形直角
三角形勾股定理勾股定理的逆定理“斜边、直角边定理” 是判定两个直角三角形全等所独有的,在运用该判定定理时,要注意全等的前提条件是两个直角三角形.
2. 要注意本章中的互逆命题,如直角三角形的性质和判定定理,勾股定理及其逆定理,角平分线的性质定理及其逆定理等,它们都是互为逆命题.
3. 勾股定理及其逆定理都体现了数形结合的思想. 勾股定理体现了由形到数,而勾股定理的逆定理是用代数方法来研究几何问题,体现了由数到形.结 束
∴ ∠PDO =∠PEO = 90°.在△PDO和△PEO中,
∵ ∠PDO =∠PEO,
∠DOP =∠EOP,
OP = OP,∴ △PDO≌△PEO.∴ PD = PE.我们来证明这个结论.图1-26图1-26角的平分线上的点到角的两边的距离相等.
由此得到角平分线的性质定理:在Rt△PDO和Rt△PEO中,
∵ OP = OP,PD = PE,
∴ Rt△PDO≌Rt△PEO.∵ PD⊥OA, PE⊥OB,
∴ ∠PDO =∠PEO = 90°.如图1-27,过点O,P作射线OC.∴ ∠AOC =∠BOC.∴ OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.角的内部到角的两边距离相等的点在角的平分线上.
由此得到角平分线的性质定理的逆定理:又 BA⊥AD, BC⊥CD,∴ 点B在∠ADC的平分线上.(1)求证:点B在∠ADC的平分线上;图1-28证明: 在Rt△BAD和Rt△BCD中,
∵ BA = BC, BD = BD,∴ Rt△BAD≌Rt△BCD.∴ ∠ABD =∠CBD.∴ BD是∠ABC的平分线.(2)求证:BD是∠ABC的平分线.
解 作∠AOB的角平分线,交MN于一点,则这点即为所
求作的点P.(提示:用尺规作图)如图,在直线MN上求作一点P ,使点P到∠AOB两边
的距离相等.P2. 如图,在△ABC 中,AD 平分∠BAC, DE⊥AB
于点E,DF⊥AC 于点F,BD=CD.
求证:AB=AC. 如图1-29, 已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF 的中点. 需添加一个什么条件, 就可使CM,AM
分别为∠ACD和∠CAB的平分线呢?图1-29图1-29∵ ME⊥CD, MN⊥CA,同理可得AM是∠CAB的平分线.可以添加条件MN =ME (或MN =MF).∴ M在∠ACD的平分线上,即CM是∠ACD的平分线.图1-29∴ PE=PF.在△EBP中,BE+PE>PB,∴ BE+PF>PB.图1-30 如图1-31,你能在△ABC 中找到一点P,使其
到三边的距离相等吗?图1-31如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.2. 如图,在△ABC 中,AD⊥DE,BE⊥DE,AC,
BC 分别平分∠BAD,∠ABE,点C在线段DE上.
求证:AB=AD+BE.M证明 作CM⊥AB于点M. 1. 直角三角形的两个锐角有什么关系?
2. 直角三角形斜边上的中线与斜边有什么关系?
3. 请用自己的语言叙述勾股定理及其逆定理.
4. 判断两个直角三角形全等的方法有哪些?
5. 角平分线有哪些性质?
直角三角形斜边上的中线等于斜边的一半有两个角互余的三角形是直角三角形直角
三角形勾股定理勾股定理的逆定理“斜边、直角边定理” 是判定两个直角三角形全等所独有的,在运用该判定定理时,要注意全等的前提条件是两个直角三角形.
2. 要注意本章中的互逆命题,如直角三角形的性质和判定定理,勾股定理及其逆定理,角平分线的性质定理及其逆定理等,它们都是互为逆命题.
3. 勾股定理及其逆定理都体现了数形结合的思想. 勾股定理体现了由形到数,而勾股定理的逆定理是用代数方法来研究几何问题,体现了由数到形.结 束
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
