湘教版2014-2015学年八年级数学下册精品课件:2.1多边形(共32张PPT)
文档属性
| 名称 | 湘教版2014-2015学年八年级数学下册精品课件:2.1多边形(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-15 00:00:00 | ||
图片预览





文档简介
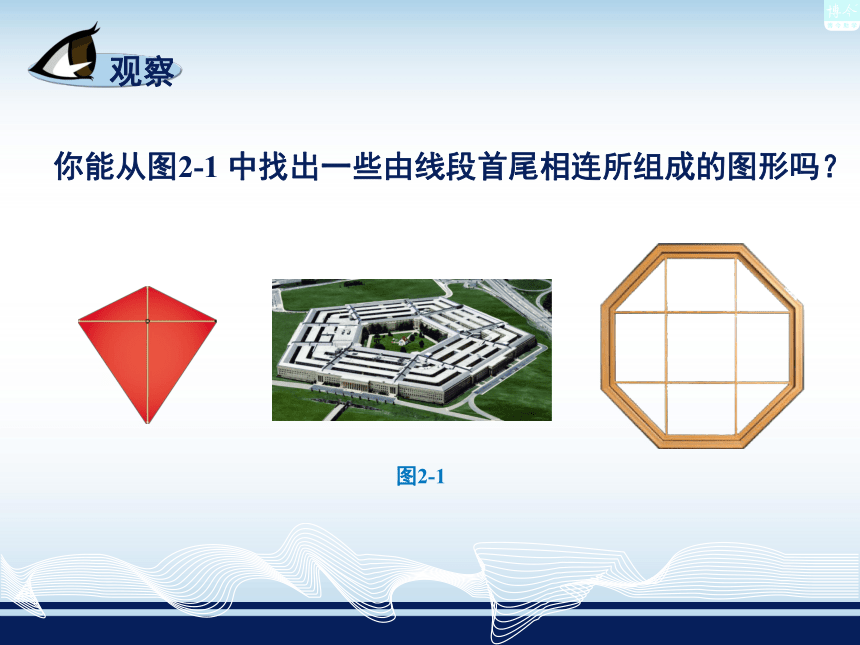
课件32张PPT。2.1多 边 形你能从图2-1 中找出一些由线段首尾相连所组成的图形吗?图2-1 在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形.组成多边形的各条线段叫作多边形的边.相邻两条边的公共端点叫作多边形的顶点.连接不相邻的两个顶点的线段叫作多边形的对角线. 相邻两边组成的角叫作多边形的内角,简称多边形的角.
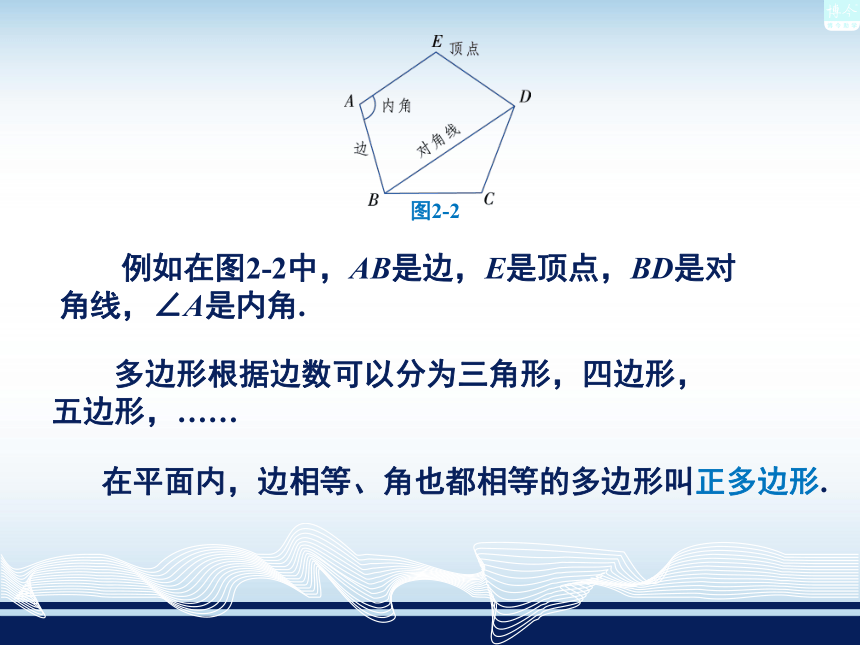
例如在图2-2中,AB是边,E是顶点,BD是对角线,∠A是内角.在平面内,边相等、角也都相等的多边形叫正多边形. 多边形根据边数可以分为三角形,四边形,
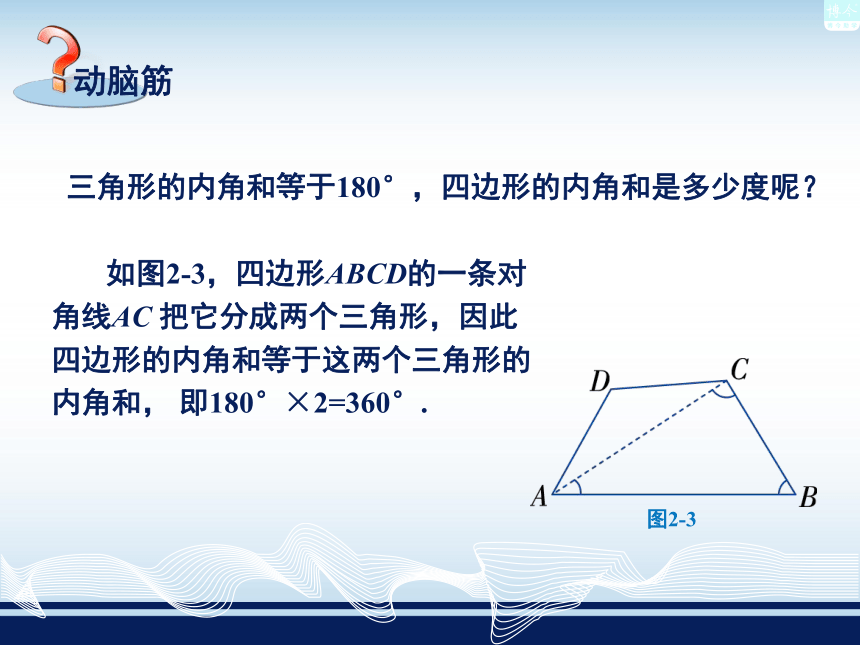
五边形,……图2-2三角形的内角和等于180°,四边形的内角和是多少度呢? 如图2-3,四边形ABCD的一条对
角线AC 把它分成两个三角形,因此
四边形的内角和等于这两个三角形的
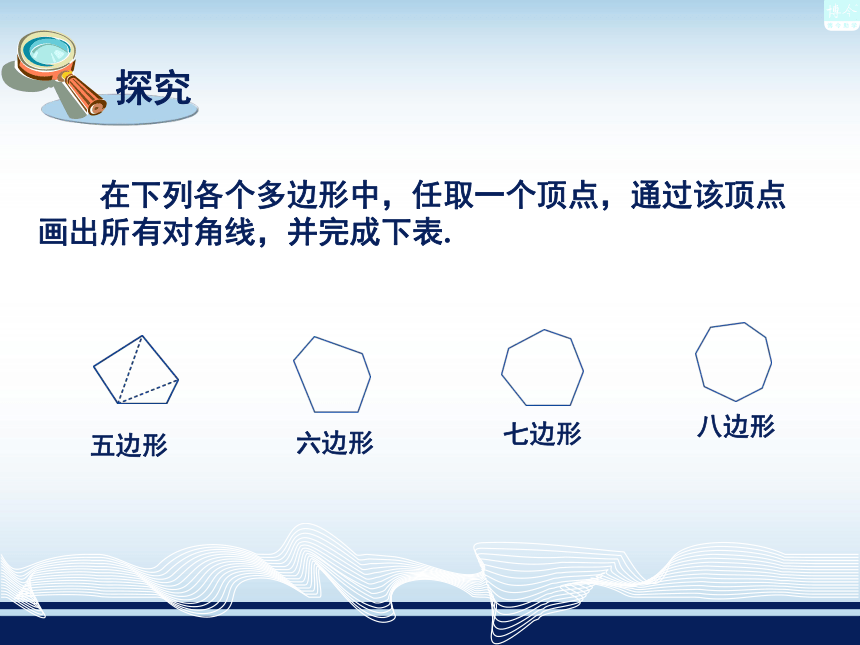
内角和, 即180°×2=360°.图2-3 在下列各个多边形中,任取一个顶点,通过该顶点
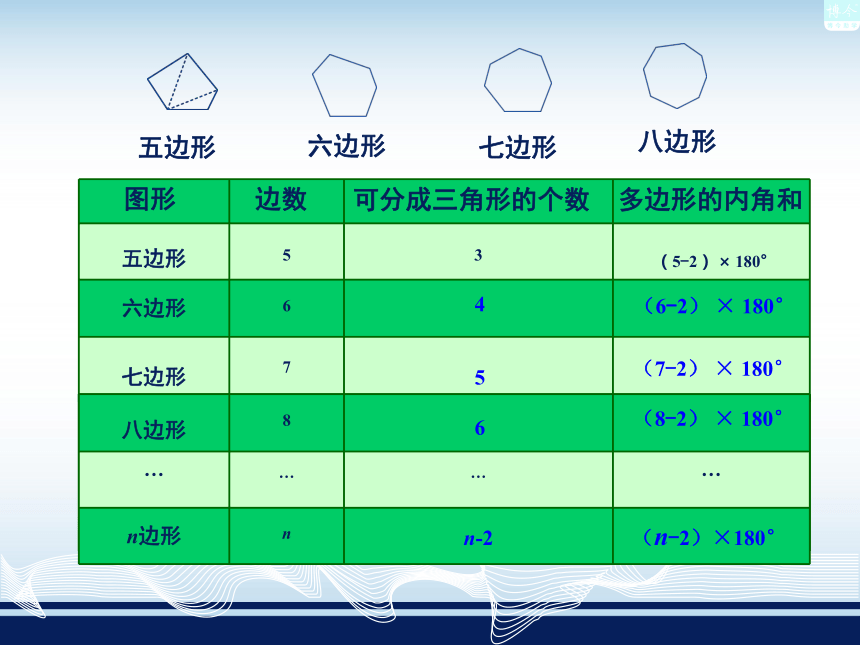
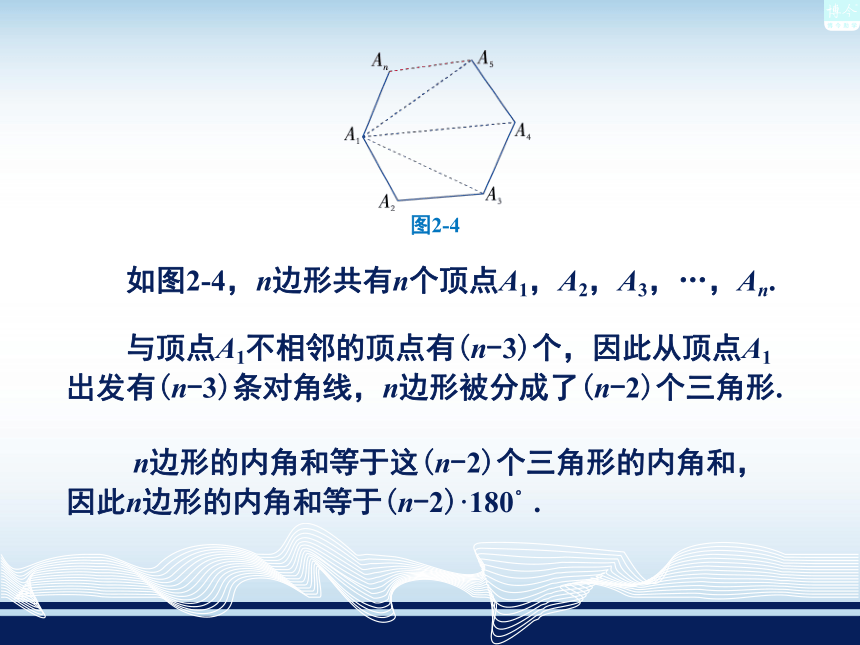
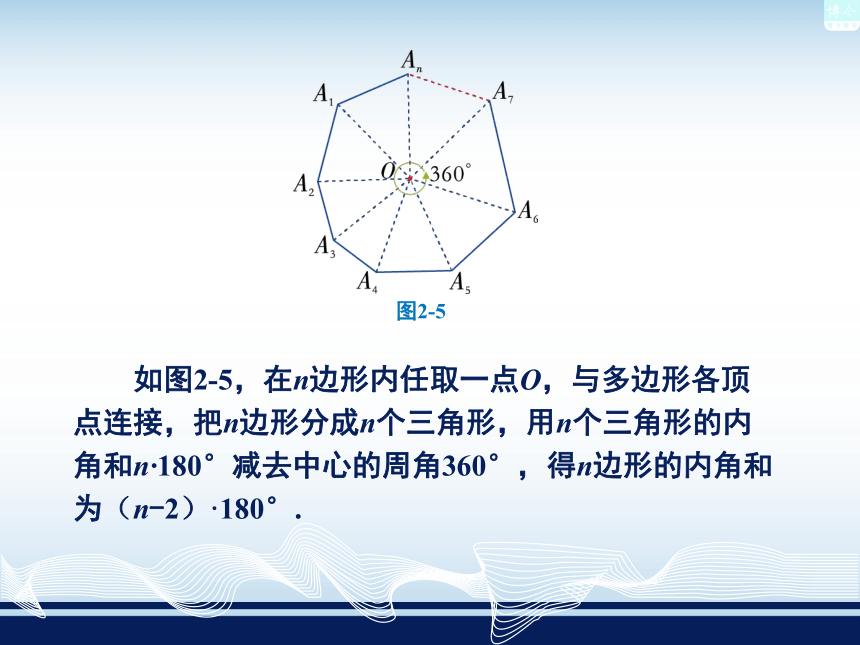
画出所有对角线,并完成下表.图形 边数可分成三角形的个数多边形的内角和4(6-2) × 180°(7-2) × 180°5(8-2) × 180°6n-2(n-2)×180° 如图2-4,n边形共有n个顶点A1,A2,A3,…,An. 与顶点A1不相邻的顶点有(n-3)个,因此从顶点A1出发有(n-3)条对角线,n边形被分成了(n-2)个三角形. n边形的内角和等于这(n-2)个三角形的内角和,因此n边形的内角和等于(n-2)·180°.图2-4n边形的内角和等于(n-2)· 180°由此得出:你还可以用其他方法探究n边形的内角和公式吗?例1(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,
它是几边形?
举
例(2)设这个多边形的边数为n,则
(n-2 )×180°= 1980°,
解得n = 13.
所以这是一个十三边形.(1)正十二边形的每一个内角是多少度?(2)一个多边形的内角和等于1800°,它是几边形?答:150°.
答:十二边形.过多边形某个顶点的所有对角线,将这个多边形
分成10个三角形,那么这个多边形是几边形?答:十二边形. 如图2-6,∠EDF是五边形ABCDE的一个外角.
在多边形的每个顶点处取一个外角,它们的和叫作
这个多边形的外角和. 多边形的内角的一边与另一边的反向延长线所组
成的角叫作这个多边形的一个外角.图2-6 我们已经知道三角形的外角和为360°,那么
四边形的外角和为多少度呢? 如图2-7,在四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∴ ∠1 +∠2 +∠3 +∠4 = 4 × 180° - 360° = 360°.∵ ∠1 +∠DAB = 180°,∠2 +∠ABC = 180°,
∠3 +∠BCD = 180°, ∠4 +∠ADC = 180°,
又 ∠DAB +∠ABC +∠BCD +∠ADC = 360°,∴ 四边形的外角和为360°.
图2-7 三角形的外角和是360°,四边形的外角和是360°,n边形(n为不小于3的任意整数)的外角
和都是360°吗?n边形的外角和与边数有关系吗? 类似于求四边形外角和的思路,在n边形的每一
个顶点处取一个外角,其中每一个外角与它相邻的内
角之和为180°. 因此,这n个外角与跟它相邻的内角之
和加起来是n· 180°,将这个总和减去n边形的内角和
(n-2 )×180°所得的差即为n边形的外角和.n· 180°-(n-2 )×180°
=[n-(n-2 )]· 180°
= 2×180°
= 360° . n 边形的外角
和与边数没有关系.任意多边形的外角和等于360°.由此得出:例2 一个多边形的内角和等于它外角和
的5倍,它是几边形?举
例解 设多边形的边数为n,则它的内角和等于(n-2)· 180°.由题意得
(n-2)· 180°=5×360°,解得 n=12.因此这个多边形是十二边形. 三角形具有稳定性, 那么四边形呢?用4 根木条
钉成如图2-8 的木框,随意扭转四边形的边,它的形状会发生变化吗?图2-8 我们发现,四边形的边长不变,但它的形状改
变了, 这说明四边形具有不稳定性. 在实际生活中,我们经常利用四边形的不稳定性,
例如图2-9 (a)中的电动伸缩门、图2-9 (b)中的升降器.
有时又要克服四边形的不稳定性,例如在图2-9 (c)中的
栅栏两横梁之间加钉斜木条,构成三角形,这是为了利用
三角形的稳定性.
图2-9(a)(c)(b)1. 一个多边形的每一个外角都等于45°,
这个多边形是几边形?它的每一个内角
是多少度?答:这个多边形是八边形,
每个内角是135°.2. 如图,求图中x的值.答:x =60°.3. 举出日常生活中利用四边形不稳定性的一些例子..答:有种衣架是根据平行四边形的不稳定性,用同样
长的木条构成的几个相连的菱形,每个顶点处都
有一个挂钩,不仅美观,而且实用,如下图: 答:有种衣架是根据平行四边形的不稳定性,用同样
长的木条构成的几个相连的菱形,每个顶点处都
有一个挂钩,不仅美观,而且实用,如下图: 液晶电视的双臂旋转伸缩可悬挂支架也用到了四边形
的不稳定性,调节幅度大,可上下左右及前后多方向
调节满足客户观看需要,如下图:例1 若一个正多边形的一个外角是40°,则这个正多边形的边数是 ( )
A. 10 B.9 C.8 D.6B例2 某多边形的内角和是其外角和的3倍,则此多边形的边数是 ( )
A. 5 B.6 C.7 D.8D例3 当多边形的边数增加1时,它的内角和与外角和 ( )
A. 都不变.
B. 内角和增加180°,外角和不变
C. 内角和增加180°,外角和减少180°. D. 都增加180°.B结 束
例如在图2-2中,AB是边,E是顶点,BD是对角线,∠A是内角.在平面内,边相等、角也都相等的多边形叫正多边形. 多边形根据边数可以分为三角形,四边形,
五边形,……图2-2三角形的内角和等于180°,四边形的内角和是多少度呢? 如图2-3,四边形ABCD的一条对
角线AC 把它分成两个三角形,因此
四边形的内角和等于这两个三角形的
内角和, 即180°×2=360°.图2-3 在下列各个多边形中,任取一个顶点,通过该顶点
画出所有对角线,并完成下表.图形 边数可分成三角形的个数多边形的内角和4(6-2) × 180°(7-2) × 180°5(8-2) × 180°6n-2(n-2)×180° 如图2-4,n边形共有n个顶点A1,A2,A3,…,An. 与顶点A1不相邻的顶点有(n-3)个,因此从顶点A1出发有(n-3)条对角线,n边形被分成了(n-2)个三角形. n边形的内角和等于这(n-2)个三角形的内角和,因此n边形的内角和等于(n-2)·180°.图2-4n边形的内角和等于(n-2)· 180°由此得出:你还可以用其他方法探究n边形的内角和公式吗?例1(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,
它是几边形?
举
例(2)设这个多边形的边数为n,则
(n-2 )×180°= 1980°,
解得n = 13.
所以这是一个十三边形.(1)正十二边形的每一个内角是多少度?(2)一个多边形的内角和等于1800°,它是几边形?答:150°.
答:十二边形.过多边形某个顶点的所有对角线,将这个多边形
分成10个三角形,那么这个多边形是几边形?答:十二边形. 如图2-6,∠EDF是五边形ABCDE的一个外角.
在多边形的每个顶点处取一个外角,它们的和叫作
这个多边形的外角和. 多边形的内角的一边与另一边的反向延长线所组
成的角叫作这个多边形的一个外角.图2-6 我们已经知道三角形的外角和为360°,那么
四边形的外角和为多少度呢? 如图2-7,在四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∴ ∠1 +∠2 +∠3 +∠4 = 4 × 180° - 360° = 360°.∵ ∠1 +∠DAB = 180°,∠2 +∠ABC = 180°,
∠3 +∠BCD = 180°, ∠4 +∠ADC = 180°,
又 ∠DAB +∠ABC +∠BCD +∠ADC = 360°,∴ 四边形的外角和为360°.
图2-7 三角形的外角和是360°,四边形的外角和是360°,n边形(n为不小于3的任意整数)的外角
和都是360°吗?n边形的外角和与边数有关系吗? 类似于求四边形外角和的思路,在n边形的每一
个顶点处取一个外角,其中每一个外角与它相邻的内
角之和为180°. 因此,这n个外角与跟它相邻的内角之
和加起来是n· 180°,将这个总和减去n边形的内角和
(n-2 )×180°所得的差即为n边形的外角和.n· 180°-(n-2 )×180°
=[n-(n-2 )]· 180°
= 2×180°
= 360° . n 边形的外角
和与边数没有关系.任意多边形的外角和等于360°.由此得出:例2 一个多边形的内角和等于它外角和
的5倍,它是几边形?举
例解 设多边形的边数为n,则它的内角和等于(n-2)· 180°.由题意得
(n-2)· 180°=5×360°,解得 n=12.因此这个多边形是十二边形. 三角形具有稳定性, 那么四边形呢?用4 根木条
钉成如图2-8 的木框,随意扭转四边形的边,它的形状会发生变化吗?图2-8 我们发现,四边形的边长不变,但它的形状改
变了, 这说明四边形具有不稳定性. 在实际生活中,我们经常利用四边形的不稳定性,
例如图2-9 (a)中的电动伸缩门、图2-9 (b)中的升降器.
有时又要克服四边形的不稳定性,例如在图2-9 (c)中的
栅栏两横梁之间加钉斜木条,构成三角形,这是为了利用
三角形的稳定性.
图2-9(a)(c)(b)1. 一个多边形的每一个外角都等于45°,
这个多边形是几边形?它的每一个内角
是多少度?答:这个多边形是八边形,
每个内角是135°.2. 如图,求图中x的值.答:x =60°.3. 举出日常生活中利用四边形不稳定性的一些例子..答:有种衣架是根据平行四边形的不稳定性,用同样
长的木条构成的几个相连的菱形,每个顶点处都
有一个挂钩,不仅美观,而且实用,如下图: 答:有种衣架是根据平行四边形的不稳定性,用同样
长的木条构成的几个相连的菱形,每个顶点处都
有一个挂钩,不仅美观,而且实用,如下图: 液晶电视的双臂旋转伸缩可悬挂支架也用到了四边形
的不稳定性,调节幅度大,可上下左右及前后多方向
调节满足客户观看需要,如下图:例1 若一个正多边形的一个外角是40°,则这个正多边形的边数是 ( )
A. 10 B.9 C.8 D.6B例2 某多边形的内角和是其外角和的3倍,则此多边形的边数是 ( )
A. 5 B.6 C.7 D.8D例3 当多边形的边数增加1时,它的内角和与外角和 ( )
A. 都不变.
B. 内角和增加180°,外角和不变
C. 内角和增加180°,外角和减少180°. D. 都增加180°.B结 束
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
