2023-2024学年沪科版八年级上册数学 14.2 三角形全等的判定 第1课时课件(共19张PPT)
文档属性
| 名称 | 2023-2024学年沪科版八年级上册数学 14.2 三角形全等的判定 第1课时课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 511.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 19:20:57 | ||
图片预览





文档简介
(共19张PPT)
第十四章 全等三角形
14.2 三角形全等的判定
14.2.1 三角形全等的判定“SAS”
1.理解确定一个三角形至少需要三个条件,其中至少有一个是边长
2.理解第一个三角形全等的判定定理“边角边”,并解决简单的实际问题(重点)
一、学习目标
二、新课导入
1.什么叫全等三角形?
回顾:
能够完全重合的两个三角形叫全等三角形;
2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等;
二、新课导入
思考:
我们知道全等三角形的对应边相等,对应角相等全等的性质,那如何证明下面的两个三角形全等呢?
三、概念剖析
1.思考:如何确定一个三角形?
(一)确定三角形的条件
①三角形有六个基本元素(三条边和三个角),只给定一个元素可以是一条边或一个角;只给定两个元素,可以是两条边、两个角、一条边和一个角.
②只给定一个元素,即一条边长或一个角,对应顶点确定一个三角形的形状、大小;只给定两个元素,即两条边长或对应边或一条边和一个角,对应角确定一个三角形的形状、大小.
三、概念剖析
2.讨论:根据上面确定三角形的条件回答问题?
(二)全等三角形的判定 “边角边”
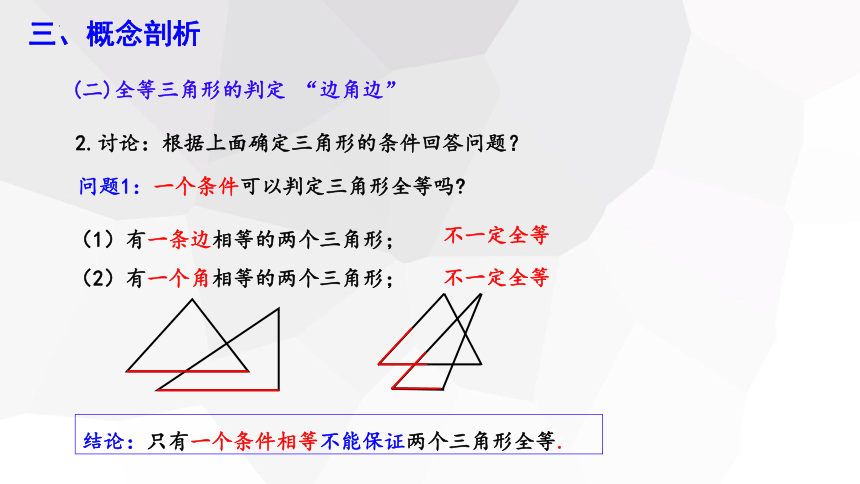
问题1:一个条件可以判定三角形全等吗
(1)有一条边相等的两个三角形;
(2)有一个角相等的两个三角形;
不一定全等
不一定全等
结论:只有一个条件相等不能保证两个三角形全等.
三、概念剖析
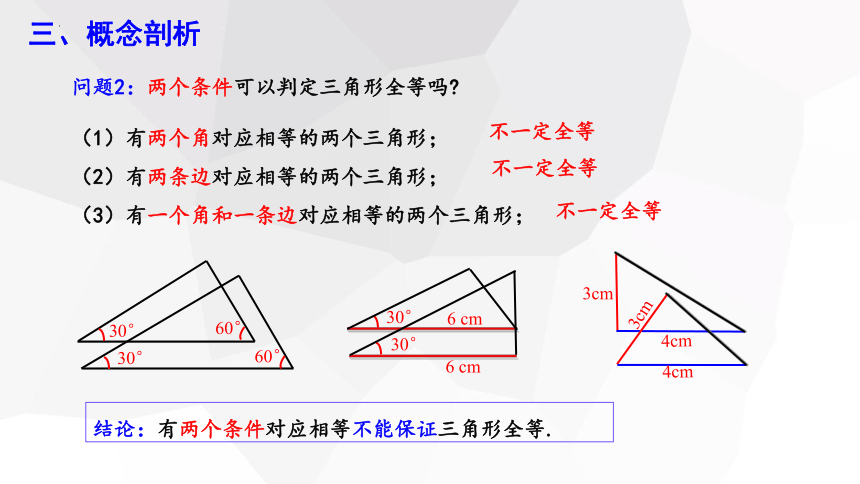
问题2:两个条件可以判定三角形全等吗
(1)有两个角对应相等的两个三角形;
(2)有两条边对应相等的两个三角形;
(3)有一个角和一条边对应相等的两个三角形;
不一定全等
不一定全等
不一定全等
60°
30°
60°
30°
3cm
4cm
3cm
4cm
6 cm
30°
30°
6 cm
结论:有两个条件对应相等不能保证三角形全等.
三、概念剖析
问题3:已知两边及其夹角可以判断三角形全等吗?
50°
2cm
2.5cm
50°
2cm
2.5cm
如图在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 将这两个三角形叠在一起,它们能完全重合,由此你能得到什么结论?
三、概念剖析
3.结论:
(二)全等三角形的判定 “边角边”
两边和它们的夹角对应相等的两个三角形全等,简记为“边角边”或“SAS”
(S表示边,A表示角).
注意:在利用这个“边角边”(SAS)判定两个三角形全等时,一定要注意两个三角形的“两边”和“夹角”中边与角对应关系.
三、概念剖析
4.“SAS”判定方法的记法
(二)全等三角形的判定 “边角边”
符号语言:
在△ABC和△DEF中,AC=DF,∠A=∠D,AB=DE,
∴△ABC≌ DEF(SAS).
四、典型例题
例1.已知:如图,点B,E在线段AD上,AB=DE,AC=DF,AC∥DF,求证:BC=EF.
证明:∵AC∥EF;∴∠A=∠D;
∵AB=DE、 ∠A=∠D 、AC=DF;(已知)
∴△ABC≌△DEF (SAS)
∴BC=EF(全等三角形的对应边相等)
四、典型例题
练一练:
又∵AE=CF,∴AE+EF=CF+EF(等式的性质),即AF=CE.
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS)
1.如图,AD∥BC,AD=CB,AE=CF.求证:AFD≌△CEB.
解:证明:∵AD∥BC(已知), ∴∠A=∠C(两直线平行,内错角相等),
①AD=CB(已知),
②∠A=∠C(已证),
③AF=CE(已证)
四、典型例题
例2.如图,在△ABC中,AB=AC,AD平分∠BAC.求证:BD=CD.
在△ABD与△ACD中,
∴△ABD≌△ACD(SAS),
∴BD=CD(全等三角形对应边相等).
证明如下:∵AD平分∠BAC(已知),∴∠BAD=∠CAD(角平分线定义).
①AB=AC,(已知)
②∠BAD=∠CAD,(已证)
③AD=AD,(公共边)
2.已知:AD=CD,DB平分∠ADC ,求证:∠A=∠C.
在△ABD与△CBD中
∴△ABD≌△CBD(SAS)
∴∠A=∠C
四、典型例题
练一练:
解:证明:∵DB平分∠ADC,∴∠1=∠2
① AD=CD (已知)
② ∠1=∠2(已证)
③ BD=BD(公共边)
例3.已知:如图,点B,E在线段AD上,AC=DC,运用所学知识,补充一个条件,证明:AB=DE.
四、典型例题
解:补充:“ BC=EC ”;
∵AC=DC、∠ACB=∠DCE(对顶角相等),BC=EC;
∴△ABC≌△DEC(SAS)
∴AB=DE(全等三角形的对应边相等)
四、典型例题
练一练:
3.如图,∠ACB=∠DBC,且在△ABC中,AB=3,AC=4,要证△ABC≌△DCB,则( )
A.BD=4 B.BC=3 C.CD=3 D.AD=4
A
解:补充:“BD=4,即BD=AC ”;
∵BD=AC、∠ACB=∠DBC(已知),CB=BC(公共边),
∴△ABC≌△DCB(SAS)
【当堂检测】
1.如图所示的全等的三角形是( )
A Ⅰ和Ⅱ B. Ⅱ和Ⅳ C.Ⅱ和Ⅲ D. Ⅰ和Ⅲ
D
2.如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC、BC并延长到点D、E,使CD=CA、CE=CB. 连接DE,量出DE的长就是A、B的距离,这是为什么
【当堂检测】
C
·
A
E
分析:在△ABC 和△DEC中:AC=DC、
解:CB=EC(已知),∠ACB=∠DCE(对顶角相等),
∴△ABC ≌△DEC (SAS)
∴AB=DE(全等三角形的对应边相等)
B
D
五、课堂总结
第十四章 全等三角形
14.2 三角形全等的判定
14.2.1 三角形全等的判定“SAS”
1.理解确定一个三角形至少需要三个条件,其中至少有一个是边长
2.理解第一个三角形全等的判定定理“边角边”,并解决简单的实际问题(重点)
一、学习目标
二、新课导入
1.什么叫全等三角形?
回顾:
能够完全重合的两个三角形叫全等三角形;
2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等;
二、新课导入
思考:
我们知道全等三角形的对应边相等,对应角相等全等的性质,那如何证明下面的两个三角形全等呢?
三、概念剖析
1.思考:如何确定一个三角形?
(一)确定三角形的条件
①三角形有六个基本元素(三条边和三个角),只给定一个元素可以是一条边或一个角;只给定两个元素,可以是两条边、两个角、一条边和一个角.
②只给定一个元素,即一条边长或一个角,对应顶点确定一个三角形的形状、大小;只给定两个元素,即两条边长或对应边或一条边和一个角,对应角确定一个三角形的形状、大小.
三、概念剖析
2.讨论:根据上面确定三角形的条件回答问题?
(二)全等三角形的判定 “边角边”
问题1:一个条件可以判定三角形全等吗
(1)有一条边相等的两个三角形;
(2)有一个角相等的两个三角形;
不一定全等
不一定全等
结论:只有一个条件相等不能保证两个三角形全等.
三、概念剖析
问题2:两个条件可以判定三角形全等吗
(1)有两个角对应相等的两个三角形;
(2)有两条边对应相等的两个三角形;
(3)有一个角和一条边对应相等的两个三角形;
不一定全等
不一定全等
不一定全等
60°
30°
60°
30°
3cm
4cm
3cm
4cm
6 cm
30°
30°
6 cm
结论:有两个条件对应相等不能保证三角形全等.
三、概念剖析
问题3:已知两边及其夹角可以判断三角形全等吗?
50°
2cm
2.5cm
50°
2cm
2.5cm
如图在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 将这两个三角形叠在一起,它们能完全重合,由此你能得到什么结论?
三、概念剖析
3.结论:
(二)全等三角形的判定 “边角边”
两边和它们的夹角对应相等的两个三角形全等,简记为“边角边”或“SAS”
(S表示边,A表示角).
注意:在利用这个“边角边”(SAS)判定两个三角形全等时,一定要注意两个三角形的“两边”和“夹角”中边与角对应关系.
三、概念剖析
4.“SAS”判定方法的记法
(二)全等三角形的判定 “边角边”
符号语言:
在△ABC和△DEF中,AC=DF,∠A=∠D,AB=DE,
∴△ABC≌ DEF(SAS).
四、典型例题
例1.已知:如图,点B,E在线段AD上,AB=DE,AC=DF,AC∥DF,求证:BC=EF.
证明:∵AC∥EF;∴∠A=∠D;
∵AB=DE、 ∠A=∠D 、AC=DF;(已知)
∴△ABC≌△DEF (SAS)
∴BC=EF(全等三角形的对应边相等)
四、典型例题
练一练:
又∵AE=CF,∴AE+EF=CF+EF(等式的性质),即AF=CE.
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS)
1.如图,AD∥BC,AD=CB,AE=CF.求证:AFD≌△CEB.
解:证明:∵AD∥BC(已知), ∴∠A=∠C(两直线平行,内错角相等),
①AD=CB(已知),
②∠A=∠C(已证),
③AF=CE(已证)
四、典型例题
例2.如图,在△ABC中,AB=AC,AD平分∠BAC.求证:BD=CD.
在△ABD与△ACD中,
∴△ABD≌△ACD(SAS),
∴BD=CD(全等三角形对应边相等).
证明如下:∵AD平分∠BAC(已知),∴∠BAD=∠CAD(角平分线定义).
①AB=AC,(已知)
②∠BAD=∠CAD,(已证)
③AD=AD,(公共边)
2.已知:AD=CD,DB平分∠ADC ,求证:∠A=∠C.
在△ABD与△CBD中
∴△ABD≌△CBD(SAS)
∴∠A=∠C
四、典型例题
练一练:
解:证明:∵DB平分∠ADC,∴∠1=∠2
① AD=CD (已知)
② ∠1=∠2(已证)
③ BD=BD(公共边)
例3.已知:如图,点B,E在线段AD上,AC=DC,运用所学知识,补充一个条件,证明:AB=DE.
四、典型例题
解:补充:“ BC=EC ”;
∵AC=DC、∠ACB=∠DCE(对顶角相等),BC=EC;
∴△ABC≌△DEC(SAS)
∴AB=DE(全等三角形的对应边相等)
四、典型例题
练一练:
3.如图,∠ACB=∠DBC,且在△ABC中,AB=3,AC=4,要证△ABC≌△DCB,则( )
A.BD=4 B.BC=3 C.CD=3 D.AD=4
A
解:补充:“BD=4,即BD=AC ”;
∵BD=AC、∠ACB=∠DBC(已知),CB=BC(公共边),
∴△ABC≌△DCB(SAS)
【当堂检测】
1.如图所示的全等的三角形是( )
A Ⅰ和Ⅱ B. Ⅱ和Ⅳ C.Ⅱ和Ⅲ D. Ⅰ和Ⅲ
D
2.如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC、BC并延长到点D、E,使CD=CA、CE=CB. 连接DE,量出DE的长就是A、B的距离,这是为什么
【当堂检测】
C
·
A
E
分析:在△ABC 和△DEC中:AC=DC、
解:CB=EC(已知),∠ACB=∠DCE(对顶角相等),
∴△ABC ≌△DEC (SAS)
∴AB=DE(全等三角形的对应边相等)
B
D
五、课堂总结
