14.2 三角形全等的判定 (第3课时)课件 19张PPT 2023-2024学年沪科版八年级上册数学
文档属性
| 名称 | 14.2 三角形全等的判定 (第3课时)课件 19张PPT 2023-2024学年沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 917.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 21:18:27 | ||
图片预览





文档简介
(共19张PPT)
第十四章 全等三角形
14.2 三角形全等的判定
14.2.3 用“边边边”判定三角形全等
1.理解三边分别相等的两个三角形全等;
2.能用“边边边”判定两个三角形相等,解决相关几何问题;(重点)
3.理解三角形的稳定性,并会运用三角形的稳定性去解决实际问题.(难点)
一、学习目标
二、新课导入
你还记得上节课学习的判定三角形全等的方法吗?
回顾:
“ASA”:两角和它们的夹边分别相等的两个三角形全等.
思考:如图,已知一个三角形的三条边,如何作出一个与原三角形全等的三角形
二、新课导入
如图是建筑工人在施工时搭建方便通过的支架桥,它们都是类似这种三角形的形状,这样能在一定程度上保证通行时的安全,你可以说出这是什么原理吗?
三、概念剖析
(一)全等三角形的判定方法“边边边”
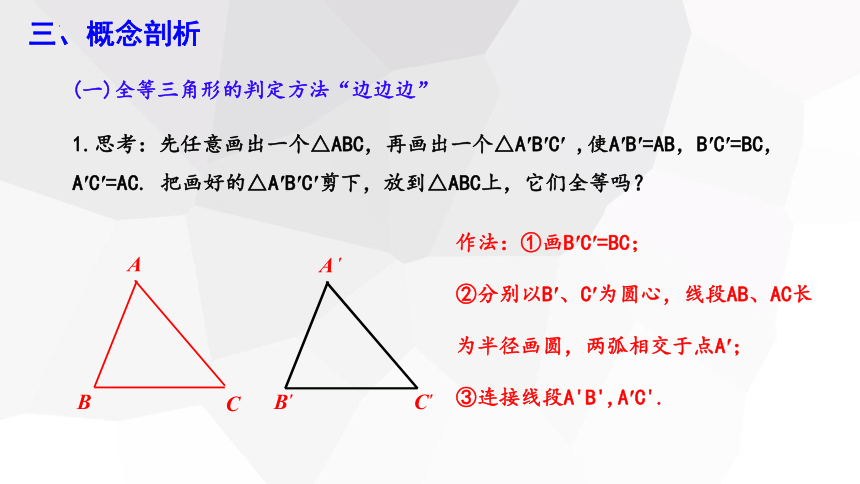
1.思考:先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′=AB,B′C′=BC,A′C′=AC. 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
作法:①画B′C′=BC;
②分别以B′、C′为圆心,线段AB、AC长为半径画圆,两弧相交于点A′;
③连接线段A'B',A′C'.
A ′
B′
C′
A
B
C
三、概念剖析
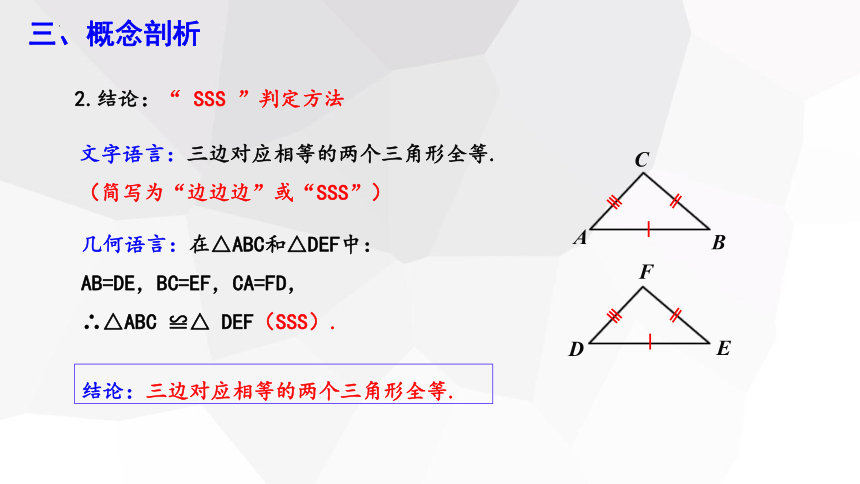
2.结论:“ SSS ”判定方法
文字语言:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
几何语言:在△ABC和△DEF中:
AB=DE,BC=EF,CA=FD,
∴△ABC ≌△ DEF(SSS).
结论:三边对应相等的两个三角形全等.
A
B
C
D
E
F
三、概念剖析
(二)三角形的稳定性
1.思考:如图,在木门的背面加钉一根木条,可以使一扇旧木门不变形和更加稳固,从而延长木门的使用寿命,你从中能发现什么?
只要三角形的三边的长度确认了,这个三角形的形状和大小就完全确定了,这个性质就叫三角形的稳定性。
三、概念剖析
2.讨论:三角形的稳定性在现实生活中有着广泛的应用,你能找出来哪些
四、典型例题
例1.如图,A、F、C、D在同一条直线上,AB=DE,BC=EF,AF=CD.求证:BC∥EF.
证明:∵AF=CD,∴AF+FC=CD+FC,即AC=DF.
在△ABC与△DEF中,
AB=DE(已知),BC=EF(已知),AC=DF(已证),
∴△ABC≌△DEF(SSS),
∴∠BCA=∠EFD.
∴BC∥EF.
四、典型例题
练一练:
1.已知:如图,AB=CD ,BC=DA. 求证:∠B=∠D.
证明:在△ABC和△CDA中:
AB=CD(已知),BC=DA(已知),AC=CA(公共边),
∴△ABC≌△CDA;(SSS)
∴∠B=∠D.
总结:可使用“SSS”判定,求解角相等问题.
四、典型例题
例2.已知:如图,AB=AC ,AH⊥BC于点H,∠1=∠2. 求证:∠3=∠4.
H
D
C
B
A
3
4
1
2
证明:在△BDH和△CDH中:
∵AH⊥BC; ∴∠BHD=∠CHD(垂直定义)
又∵DH=DH(公共边),∠1=∠2(已知);
∴△BDH≌△CDH; (ASA)
∴ BH=CH;(全等三角形对应边相等)
∵ AB=AC (已知)、 AH=AH(公共边)、BH=CH(已证);
∴△ABH≌△ACH ;(SSS)
∴∠3=∠4.(全等三角形对应角相等)
2.如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架.求证:
△ABD≌△ACD.
四、典型例题
练一练:
证明如下:∵AB=AC,AD是连接A与BC中点D,
∴BD=CD;
又在△ABD和△ACD中,
①AB=AC,(已知)
②BD=CD,(已证)
③AD=AD, (公共边)
∴△ABD≌△ACD(SSS).
例3.如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
四、典型例题
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
解:∵AB=AC,EB=EC,AE=AE ,∴△ABE≌△ACE故选B.
B
四、典型例题
练一练:
3.如图,在△ABC和△DCB中,AB=DC,AC与BD相交于点E,若不再添加任何字母与辅助线,要使△ABC≌△DCB,则还需增加的一个条件是( )
A
A.AC=BD B.AC=BC
C.BE=CE D.AE=DE
解:∵AB=DC,AC=BD,BC=CB ,∴△ABC≌△DCB故选A.
【当堂检测】
1.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋来加固电线杆,这是利用了三角形的( )
A
A.稳定性 B.灵活性
C.对称性 D.全等性
【当堂检测】
2.如图,AB=CD,AD=BC,则下列结论:①△ABC≌△CDB;②△ABC≌△CDA;③△ABD≌△CDB;④BA∥DC,正确的个数是( )
A.1个 B.2个
C.3个 D.4个
O
A
B
C
D
C
3.如图,C是BF的中点,AB=DC,AC=DF.求证:∠A=∠D
【当堂检测】
证明:在△ABC和△DCF中:
∵C是BF中点;∴BC=CF;
∵AB=DC、AC=DF(已知),
BC=CF(已证);
∴△ABC≌△DCF(SSS)
∴∠A=∠D
4.已知:如图,在△ABC中,AB=AC,点D,E在BC上,且AD=AE,BE=CD. 求证:△ABD≌△ACE.
【当堂检测】
证明:∵BE=CD;
∴BE–DE=CD–DE;即BD=CE.
在△ABD和△ACE中:
AB=AC,BD=CE,AD=AE,
∴△ABD≌△ACE(SSS).
五、课堂总结
第十四章 全等三角形
14.2 三角形全等的判定
14.2.3 用“边边边”判定三角形全等
1.理解三边分别相等的两个三角形全等;
2.能用“边边边”判定两个三角形相等,解决相关几何问题;(重点)
3.理解三角形的稳定性,并会运用三角形的稳定性去解决实际问题.(难点)
一、学习目标
二、新课导入
你还记得上节课学习的判定三角形全等的方法吗?
回顾:
“ASA”:两角和它们的夹边分别相等的两个三角形全等.
思考:如图,已知一个三角形的三条边,如何作出一个与原三角形全等的三角形
二、新课导入
如图是建筑工人在施工时搭建方便通过的支架桥,它们都是类似这种三角形的形状,这样能在一定程度上保证通行时的安全,你可以说出这是什么原理吗?
三、概念剖析
(一)全等三角形的判定方法“边边边”
1.思考:先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′=AB,B′C′=BC,A′C′=AC. 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
作法:①画B′C′=BC;
②分别以B′、C′为圆心,线段AB、AC长为半径画圆,两弧相交于点A′;
③连接线段A'B',A′C'.
A ′
B′
C′
A
B
C
三、概念剖析
2.结论:“ SSS ”判定方法
文字语言:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
几何语言:在△ABC和△DEF中:
AB=DE,BC=EF,CA=FD,
∴△ABC ≌△ DEF(SSS).
结论:三边对应相等的两个三角形全等.
A
B
C
D
E
F
三、概念剖析
(二)三角形的稳定性
1.思考:如图,在木门的背面加钉一根木条,可以使一扇旧木门不变形和更加稳固,从而延长木门的使用寿命,你从中能发现什么?
只要三角形的三边的长度确认了,这个三角形的形状和大小就完全确定了,这个性质就叫三角形的稳定性。
三、概念剖析
2.讨论:三角形的稳定性在现实生活中有着广泛的应用,你能找出来哪些
四、典型例题
例1.如图,A、F、C、D在同一条直线上,AB=DE,BC=EF,AF=CD.求证:BC∥EF.
证明:∵AF=CD,∴AF+FC=CD+FC,即AC=DF.
在△ABC与△DEF中,
AB=DE(已知),BC=EF(已知),AC=DF(已证),
∴△ABC≌△DEF(SSS),
∴∠BCA=∠EFD.
∴BC∥EF.
四、典型例题
练一练:
1.已知:如图,AB=CD ,BC=DA. 求证:∠B=∠D.
证明:在△ABC和△CDA中:
AB=CD(已知),BC=DA(已知),AC=CA(公共边),
∴△ABC≌△CDA;(SSS)
∴∠B=∠D.
总结:可使用“SSS”判定,求解角相等问题.
四、典型例题
例2.已知:如图,AB=AC ,AH⊥BC于点H,∠1=∠2. 求证:∠3=∠4.
H
D
C
B
A
3
4
1
2
证明:在△BDH和△CDH中:
∵AH⊥BC; ∴∠BHD=∠CHD(垂直定义)
又∵DH=DH(公共边),∠1=∠2(已知);
∴△BDH≌△CDH; (ASA)
∴ BH=CH;(全等三角形对应边相等)
∵ AB=AC (已知)、 AH=AH(公共边)、BH=CH(已证);
∴△ABH≌△ACH ;(SSS)
∴∠3=∠4.(全等三角形对应角相等)
2.如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架.求证:
△ABD≌△ACD.
四、典型例题
练一练:
证明如下:∵AB=AC,AD是连接A与BC中点D,
∴BD=CD;
又在△ABD和△ACD中,
①AB=AC,(已知)
②BD=CD,(已证)
③AD=AD, (公共边)
∴△ABD≌△ACD(SSS).
例3.如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
四、典型例题
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
解:∵AB=AC,EB=EC,AE=AE ,∴△ABE≌△ACE故选B.
B
四、典型例题
练一练:
3.如图,在△ABC和△DCB中,AB=DC,AC与BD相交于点E,若不再添加任何字母与辅助线,要使△ABC≌△DCB,则还需增加的一个条件是( )
A
A.AC=BD B.AC=BC
C.BE=CE D.AE=DE
解:∵AB=DC,AC=BD,BC=CB ,∴△ABC≌△DCB故选A.
【当堂检测】
1.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋来加固电线杆,这是利用了三角形的( )
A
A.稳定性 B.灵活性
C.对称性 D.全等性
【当堂检测】
2.如图,AB=CD,AD=BC,则下列结论:①△ABC≌△CDB;②△ABC≌△CDA;③△ABD≌△CDB;④BA∥DC,正确的个数是( )
A.1个 B.2个
C.3个 D.4个
O
A
B
C
D
C
3.如图,C是BF的中点,AB=DC,AC=DF.求证:∠A=∠D
【当堂检测】
证明:在△ABC和△DCF中:
∵C是BF中点;∴BC=CF;
∵AB=DC、AC=DF(已知),
BC=CF(已证);
∴△ABC≌△DCF(SSS)
∴∠A=∠D
4.已知:如图,在△ABC中,AB=AC,点D,E在BC上,且AD=AE,BE=CD. 求证:△ABD≌△ACE.
【当堂检测】
证明:∵BE=CD;
∴BE–DE=CD–DE;即BD=CE.
在△ABD和△ACE中:
AB=AC,BD=CE,AD=AE,
∴△ABD≌△ACE(SSS).
五、课堂总结
