15.1 轴对称图形 (第2课时 )课件 22张PPT 沪科版八年级上册数学
文档属性
| 名称 | 15.1 轴对称图形 (第2课时 )课件 22张PPT 沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 552.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
第十五章 轴对称图形与等腰三角形
15.1 轴对称图形
15.1 轴对称图形 第2课时
1.理解轴对称的概念,知道轴对称是一种图形变换;
2.理解两个图形成轴对称和轴对称图形的联系和区别;
3.了解轴对称的性质,会根据轴对称的性质作图.
一、学习目标
二、新课导入
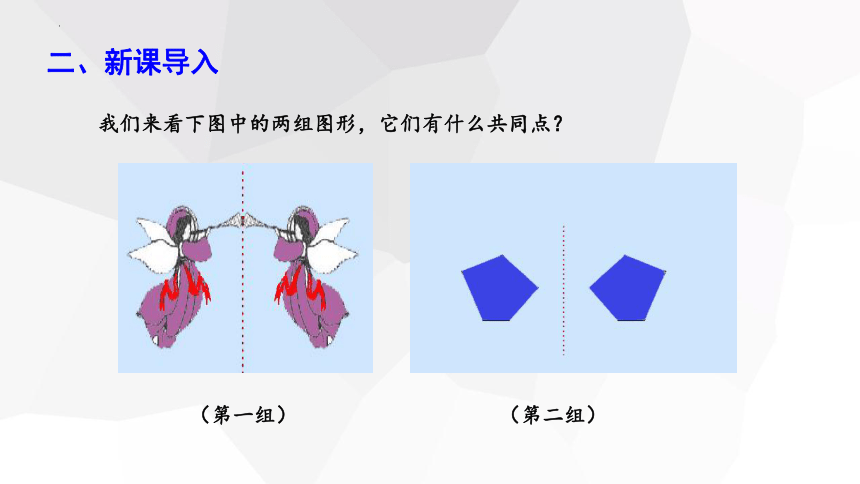
我们来看下图中的两组图形,它们有什么共同点?
(第一组)
(第二组)
三、概念剖析
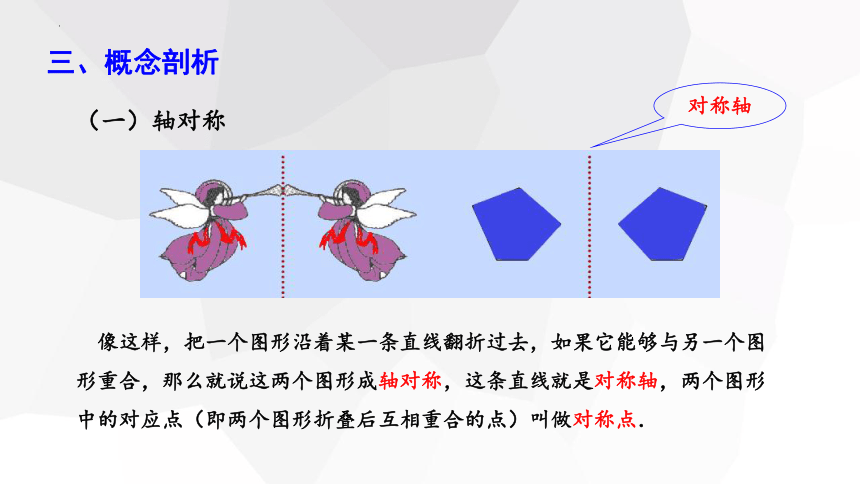
(一)轴对称
像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形折叠后互相重合的点)叫做对称点.
对称轴
三、概念剖析
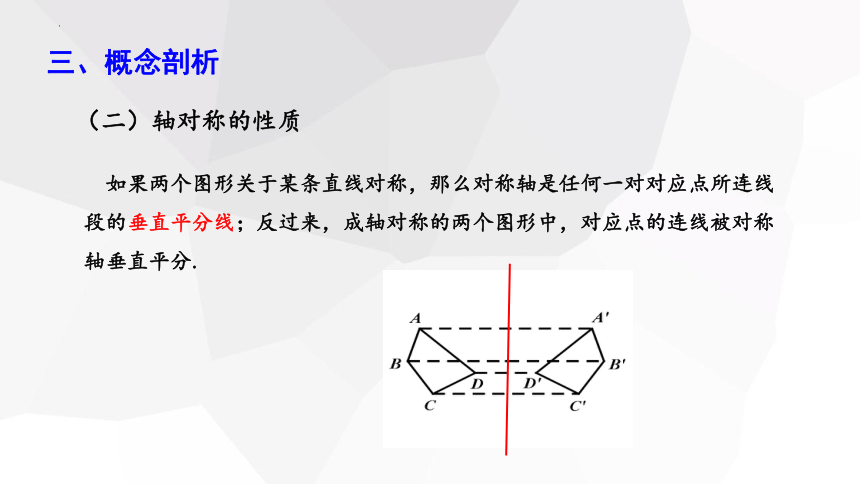
(二)轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
三、概念剖析
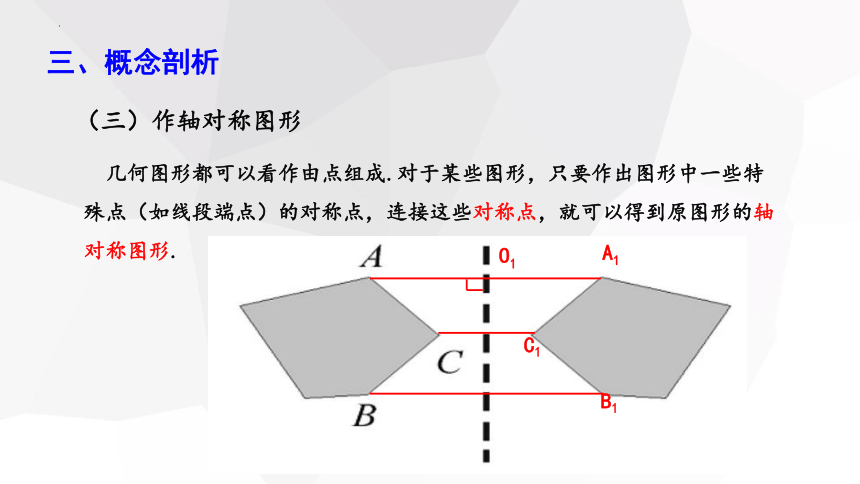
(三)作轴对称图形
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
O1
A1
B1
C1
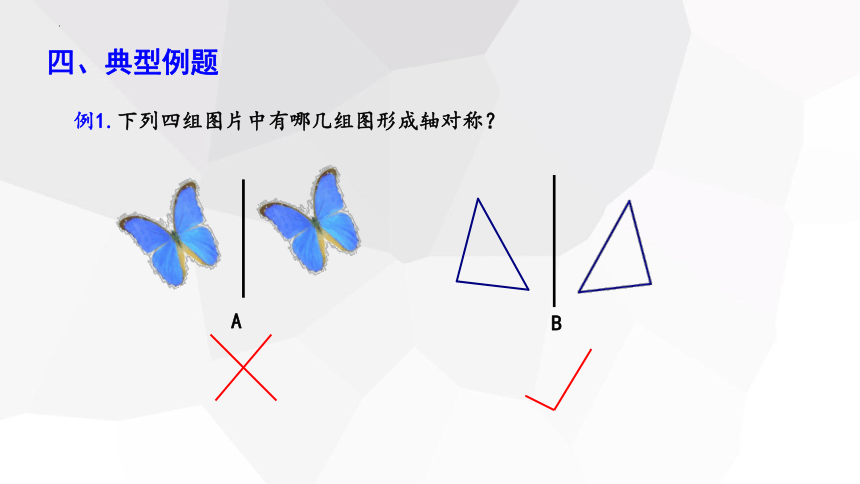
例1.下列四组图片中有哪几组图形成轴对称?
四、典型例题
B
A
四、典型例题
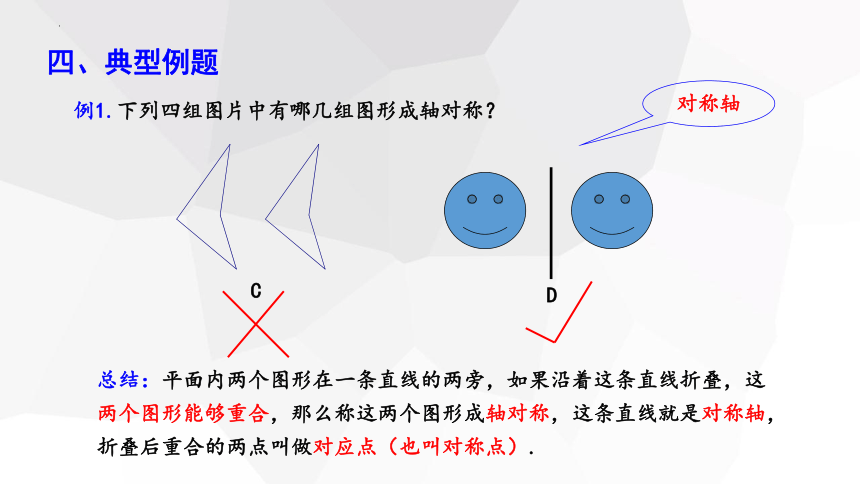
例1.下列四组图片中有哪几组图形成轴对称?
D
C
总结:平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点(也叫对称点).
对称轴
四、典型例题
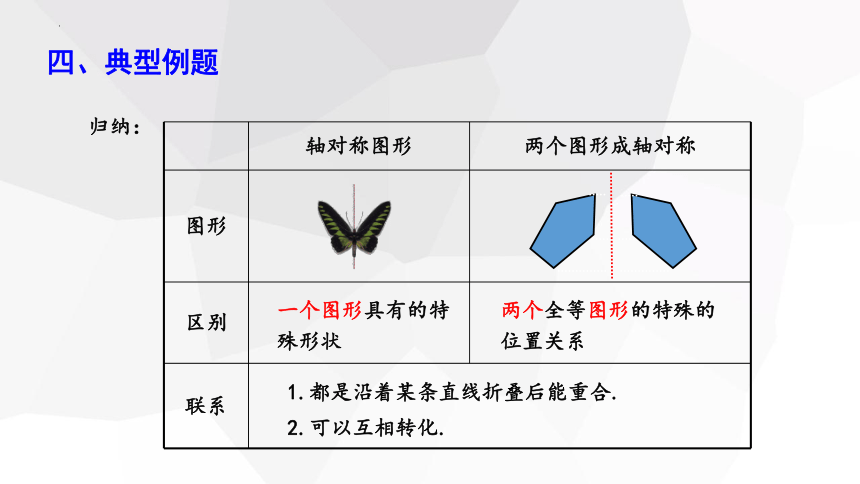
归纳:
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
【当堂检测】
点拨:轴对称的关键是寻找对称轴,对称轴两旁的部分能够互相重合.
1.下列选项中,两个图形成轴对称的是( )
A. B. C. D.
C
解析:轴对称的概念:把其中的一个图形沿着某条直线折叠,能够和另一个图形重合.根据概念可知,选项C中两个图形成轴对称.
【当堂检测】
注意轴对称和轴对称图形的区别:轴对称指的是两个图形;轴对称图形指的是一个图形.
2.如图,下列图形都是对称图形,请观察并指出 是轴对称图形, 成轴对称(填序号即可).
①③④⑥⑧
②⑤⑦
四、典型例题
例2.如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
我们说,MN是线段AA'的垂直平分线
└
所谓“关系”通常包含数量关系和位置关系
AP=A′P,∠APM= ∠A′PM=90°,MN平分线段AA′,MN⊥AA′
四、典型例题
总结:
定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
【当堂检测】
3.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
A
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
【当堂检测】
4.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 .
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半.
∵正方形ABCD的边长为4cm,
∴S阴影=4 ÷2=8(cm ).
8cm
方法归纳:正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
四、典型例题
A
B
C
例3.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
四、典型例题
作法:(1)过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△ A′B′C′即为所求.
A
B
C
A′
B′
C′
O
例3.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
四、典型例题
方法归纳:
作轴对称图形的方法:
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
【当堂检测】
5.如图,把下列图形补成关于直线l的对称图形.
【当堂检测】
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
6.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
五、课堂总结
定义:平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点(也叫对称点).
轴对称
性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
五、课堂总结
原理:对称轴是对称点连线段的垂直平分线.
画轴对称图形
方法:(1)找特征点;(2)作垂线;
(3)截取等长;(4)依次连线.
第十五章 轴对称图形与等腰三角形
15.1 轴对称图形
15.1 轴对称图形 第2课时
1.理解轴对称的概念,知道轴对称是一种图形变换;
2.理解两个图形成轴对称和轴对称图形的联系和区别;
3.了解轴对称的性质,会根据轴对称的性质作图.
一、学习目标
二、新课导入
我们来看下图中的两组图形,它们有什么共同点?
(第一组)
(第二组)
三、概念剖析
(一)轴对称
像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形折叠后互相重合的点)叫做对称点.
对称轴
三、概念剖析
(二)轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
三、概念剖析
(三)作轴对称图形
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
O1
A1
B1
C1
例1.下列四组图片中有哪几组图形成轴对称?
四、典型例题
B
A
四、典型例题
例1.下列四组图片中有哪几组图形成轴对称?
D
C
总结:平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点(也叫对称点).
对称轴
四、典型例题
归纳:
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
【当堂检测】
点拨:轴对称的关键是寻找对称轴,对称轴两旁的部分能够互相重合.
1.下列选项中,两个图形成轴对称的是( )
A. B. C. D.
C
解析:轴对称的概念:把其中的一个图形沿着某条直线折叠,能够和另一个图形重合.根据概念可知,选项C中两个图形成轴对称.
【当堂检测】
注意轴对称和轴对称图形的区别:轴对称指的是两个图形;轴对称图形指的是一个图形.
2.如图,下列图形都是对称图形,请观察并指出 是轴对称图形, 成轴对称(填序号即可).
①③④⑥⑧
②⑤⑦
四、典型例题
例2.如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
我们说,MN是线段AA'的垂直平分线
└
所谓“关系”通常包含数量关系和位置关系
AP=A′P,∠APM= ∠A′PM=90°,MN平分线段AA′,MN⊥AA′
四、典型例题
总结:
定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
【当堂检测】
3.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
A
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
【当堂检测】
4.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 .
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半.
∵正方形ABCD的边长为4cm,
∴S阴影=4 ÷2=8(cm ).
8cm
方法归纳:正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
四、典型例题
A
B
C
例3.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
四、典型例题
作法:(1)过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△ A′B′C′即为所求.
A
B
C
A′
B′
C′
O
例3.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
四、典型例题
方法归纳:
作轴对称图形的方法:
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
【当堂检测】
5.如图,把下列图形补成关于直线l的对称图形.
【当堂检测】
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
6.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
五、课堂总结
定义:平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点(也叫对称点).
轴对称
性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
五、课堂总结
原理:对称轴是对称点连线段的垂直平分线.
画轴对称图形
方法:(1)找特征点;(2)作垂线;
(3)截取等长;(4)依次连线.
