2.1.1指数与指数幂的运算
图片预览






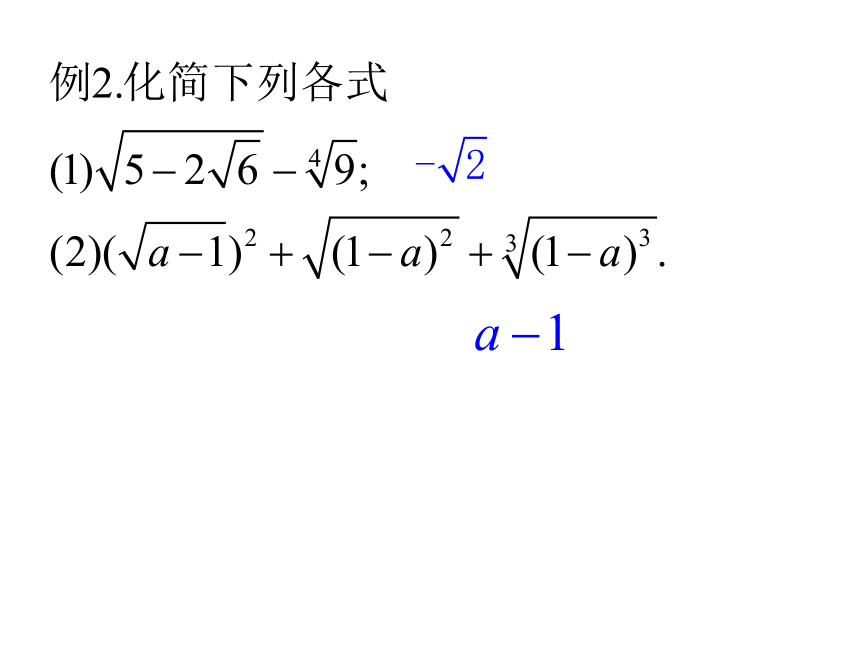
文档简介
课件22张PPT。问题1. 国务院发展研究中心在2000年分析,我国未来20年GDP(国内生产总值)年平均增长率达7.3℅,1 年后GDP为2000年的多少倍?
2 年后GDP为2000年的多少倍?
3 年后GDP为2000年的多少倍?
…
x 年后GDP为2000年的多少倍?问题2.生物死亡后,体内碳14每过5730年衰减一半(半衰期),则死亡t年后体内碳14的含量P与死亡时碳14的关系为探究该式意义?思考:当生物死亡5730年,2×5730年,3×5730年…
5000年,10000年,100000年后,它体内碳14的含量P分别为原来的多少?t=5730,2×5730,3×5730,P=?t=5000,10000,100000,P=?平方根,立方根是怎么定义的?2.1.1指数与指数幂的运算1.正数的偶次方根有两个且是相反数,
负数没有偶次方根,
零的偶次方根是零.在实数范围内,n 次方根有以下性质:2.正数的奇次方根是正数,
负数的奇次方根是负数,
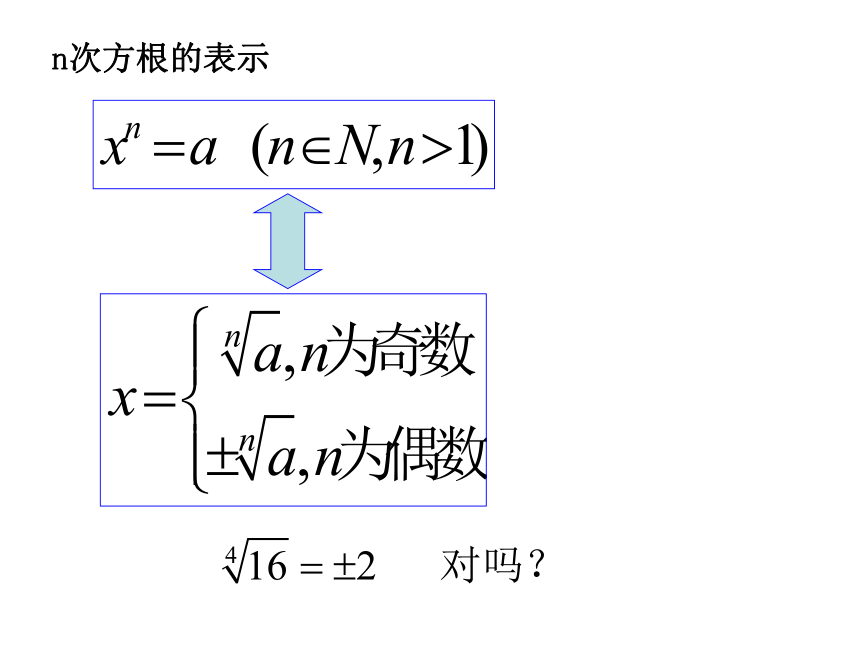
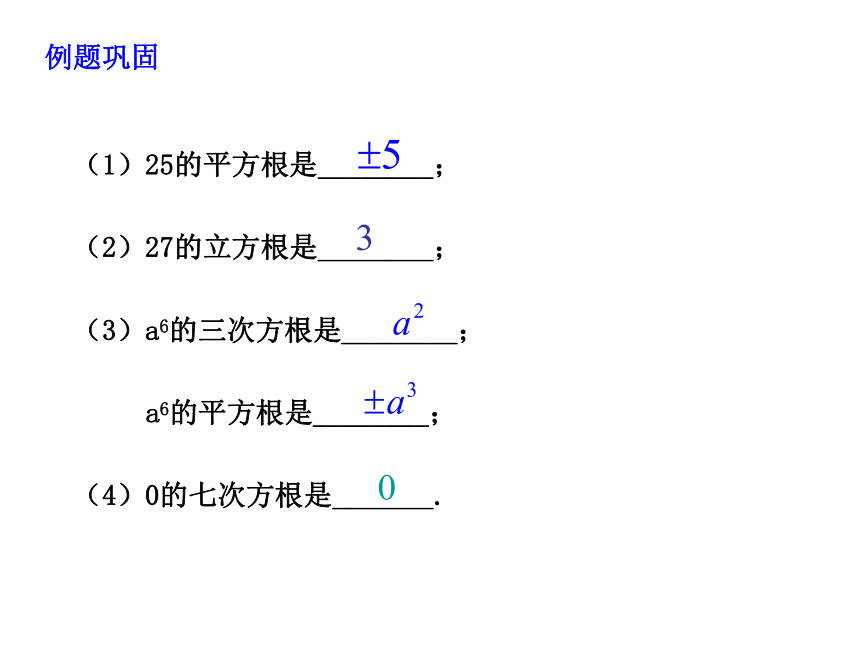
零的奇次方根是零.一.根式n次方根的表示(1)25的平方根是________;
(2)27的立方根是________;
(3)a6的三次方根是________;
a6的平方根是________;
(4)0的七次方根是_______.例题巩固二.根式的运算性质:例1.求下列各式的值例题巩固看下面几个变形:说明:(1)分数指数幂是根式的另一种表示;
(2)根式与分式指数幂可以互化.(2)0的正分数指数幂等于0;
0的负分数指数幂没意义.三.分数指数幂的定义整数指数幂的运算性质性质:(整数指数幂的运算性质对于有理指数幂也同样适用)四.分数指数幂的运算性质规定了分数指数幂的意义后,指数的概念就从整数指数推广到有理数指数.说 明:例1、求值例题巩固例2.计算下列各式(式中字母都是正数)例3.化简下列各式课堂练习简证:练一练代入得1先化简,再代入求值.1、根式和分数指数幂的意义;2、根式与分数指数幂之间的相互转化; 3、有理指数幂的含义及其运算性质. 五、知识总结无理数指数幂有理数指数幂的运算性质是否适用
于无理数指数幂? 有理数指数幂的运算性质同样适用
于无理数指数幂.整数指数幂有理数指数幂无理数指数幂根式
2 年后GDP为2000年的多少倍?
3 年后GDP为2000年的多少倍?
…
x 年后GDP为2000年的多少倍?问题2.生物死亡后,体内碳14每过5730年衰减一半(半衰期),则死亡t年后体内碳14的含量P与死亡时碳14的关系为探究该式意义?思考:当生物死亡5730年,2×5730年,3×5730年…
5000年,10000年,100000年后,它体内碳14的含量P分别为原来的多少?t=5730,2×5730,3×5730,P=?t=5000,10000,100000,P=?平方根,立方根是怎么定义的?2.1.1指数与指数幂的运算1.正数的偶次方根有两个且是相反数,
负数没有偶次方根,
零的偶次方根是零.在实数范围内,n 次方根有以下性质:2.正数的奇次方根是正数,
负数的奇次方根是负数,
零的奇次方根是零.一.根式n次方根的表示(1)25的平方根是________;
(2)27的立方根是________;
(3)a6的三次方根是________;
a6的平方根是________;
(4)0的七次方根是_______.例题巩固二.根式的运算性质:例1.求下列各式的值例题巩固看下面几个变形:说明:(1)分数指数幂是根式的另一种表示;
(2)根式与分式指数幂可以互化.(2)0的正分数指数幂等于0;
0的负分数指数幂没意义.三.分数指数幂的定义整数指数幂的运算性质性质:(整数指数幂的运算性质对于有理指数幂也同样适用)四.分数指数幂的运算性质规定了分数指数幂的意义后,指数的概念就从整数指数推广到有理数指数.说 明:例1、求值例题巩固例2.计算下列各式(式中字母都是正数)例3.化简下列各式课堂练习简证:练一练代入得1先化简,再代入求值.1、根式和分数指数幂的意义;2、根式与分数指数幂之间的相互转化; 3、有理指数幂的含义及其运算性质. 五、知识总结无理数指数幂有理数指数幂的运算性质是否适用
于无理数指数幂? 有理数指数幂的运算性质同样适用
于无理数指数幂.整数指数幂有理数指数幂无理数指数幂根式
