湘教版·2014-2015学年八年级数学下册精品课件:43一次函数的图象
文档属性
| 名称 | 湘教版·2014-2015学年八年级数学下册精品课件:43一次函数的图象 |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 08:23:04 | ||
图片预览











文档简介
课件31张PPT。一次函数的图象4.3画出正比例函数y=2x的图象.列表:先取自变量x的一些值,计算出相应的函数值,
列成表格如下:
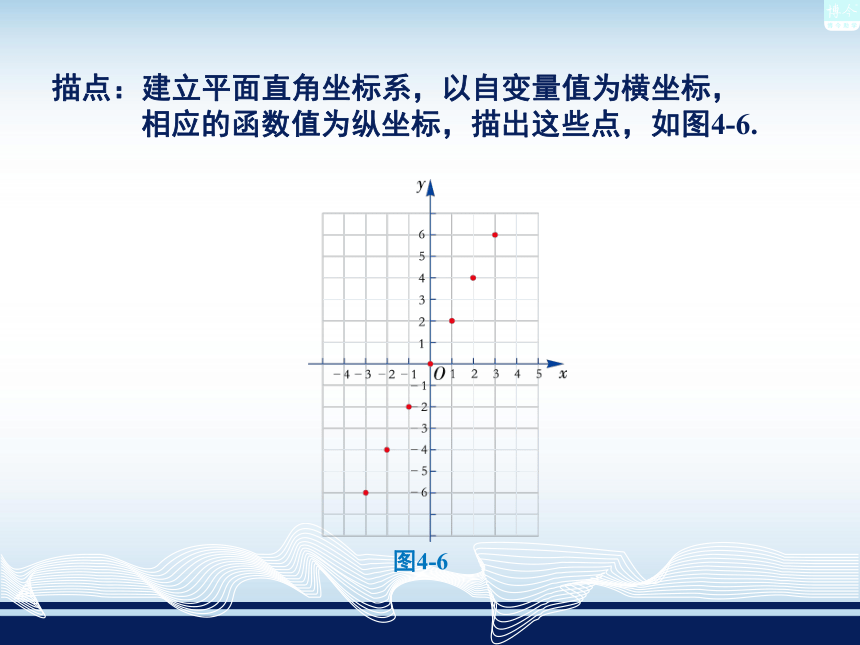
描点:建立平面直角坐标系,以自变量值为横坐标,
相应的函数值为纵坐标,描出这些点,如图4-6. 类似地,数学上已经证明:正比例函数y=kx (k 为
常数,k≠0)的图象是一条直线. 由于两点确定一条直线,
因此画正比例函数的图象,只要描出图象上的两个点,
然后过这两点作一条直线即可. 我们常常把这条直线叫作
“直线y=kx”.例1 画出正比例函数y=-2x的图象.在平面直角坐标系中描出点O(0,0)和点A(1,-2) ,
过这两点作直线,则这条直线就是y =-2x的图象,如
图4-8 所示.图4-8y=-2xA 从图4-8看出,y=-2x的图象是经过原点的一条直线.图4-8y=-2x 在平面直角坐标系中(如图4-9),任意画
一个正比例函数y=kx(k 为常数,k≠0)的图象,
它是经过原点的一条直线吗?图4-9
一般地,直线y=kx(k为常数,k≠0) 是一条经过原点的直线. 当k>0时,直线y=kx经过第三、一象限从左向右上升, 即随x的增大y也增大; 当k<0时,直线y= kx 经过第二、四象限从左向右下降,即随x的增大y反而减小.
(2)画出这个函数的图象;解: (1) y = 6x;(3)当x=3时,y=18;
当x=4时,y=24;
当x=5时,y=30. 在平面直角坐标系中, 先画出函数y = 2x 的
图象,然后探索y = 2x+3 的图象是什么样的图形,
猜测y = 2x+3的图象与y = 2x的图象有什么关系? 先取自变量x的一些值,算出y = 2x,y = 2x+3
对应的函数值,列成表格如下:y = 2x+3… -3 -2 -1 0 1 2 3 …… -6 -4 -2 0 2 4 6 …
… -3 -1 1 3 5 7 9 … 从上表可以看出,横坐标相同,y = 2x+3的
点的纵坐标比y = 2x的点的纵坐标大3,于是将
y = 2x的图象向上平移3 个单位,就得到y = 2x+3
的图象,如图4-11. 由于平移把直线变成与它平行的直线,因此
y = 2x+3的图象是与y = 2x平行的一条直线. 类似地,可以证明,一次函数y = kx+b的图
象是一条直线,它与正比例函数y = kx 的图象平
行,一次函数y = kx+b (k,b为常数,k≠0)的
图象可以看作由直线y = kx平移│b│个单位长度
而得到(当b>0时,向上平移; 当b<0时,向下平移). 由于两点确定一条直线,因此画一次函数的
图象,只要描出图象上的两个点,然后过这两点
作一条直线即可. 我们常常把这条直线叫作“直线
y = kx+b”.例3 画出一次函数y = -2x-3的图象.
在平面直角坐标系中描出两点A(0,-3),
B(1,-5),过这两点作直线,则这条直线是
一次函数y = -2x-3的图象,如图4-12. 观察画出的一次函数y = 2x+3 ,y = -2x-3的图象,
你能发现当自变量x的取值由小变大时,对应的函数
值如何变化吗? 一般地, 一次函数y = kx+b (k,b为常数,k≠0)具有如下性质:y = kx+bk > 0k < 0函数值y
的变化
函数值 y 随
自变量 x 的
增大而减小
函数值 y 随
自变量 x 的
增大而增大
例4 图4-13 描述了某一天小亮从家骑车去书店购书,
然后又骑车回家的情况. 你能说出小亮在路上的
情形吗?图4-13 第三段是与x 轴有交点的线段BC. 从横坐标看出,
小亮路上花了40min.当横坐标从60 变化到100 时,
纵坐标均匀减少,这说明小亮从书店出发匀速前进
40min,返回家中. 第二段是与x 轴平行的一条线段AB,当横坐标从30 变化到60时,纵坐标没有变化,这说明小亮在书店购书待了30min. 实际上,我们还可以比较第一段与第三段线段,
发现第一段更“陡”,这说明去书店的速度更快,
而回家的速度要慢一些.y = 3x-2y = -x结 束
列成表格如下:
描点:建立平面直角坐标系,以自变量值为横坐标,
相应的函数值为纵坐标,描出这些点,如图4-6. 类似地,数学上已经证明:正比例函数y=kx (k 为
常数,k≠0)的图象是一条直线. 由于两点确定一条直线,
因此画正比例函数的图象,只要描出图象上的两个点,
然后过这两点作一条直线即可. 我们常常把这条直线叫作
“直线y=kx”.例1 画出正比例函数y=-2x的图象.在平面直角坐标系中描出点O(0,0)和点A(1,-2) ,
过这两点作直线,则这条直线就是y =-2x的图象,如
图4-8 所示.图4-8y=-2xA 从图4-8看出,y=-2x的图象是经过原点的一条直线.图4-8y=-2x 在平面直角坐标系中(如图4-9),任意画
一个正比例函数y=kx(k 为常数,k≠0)的图象,
它是经过原点的一条直线吗?图4-9
一般地,直线y=kx(k为常数,k≠0) 是一条经过原点的直线. 当k>0时,直线y=kx经过第三、一象限从左向右上升, 即随x的增大y也增大; 当k<0时,直线y= kx 经过第二、四象限从左向右下降,即随x的增大y反而减小.
(2)画出这个函数的图象;解: (1) y = 6x;(3)当x=3时,y=18;
当x=4时,y=24;
当x=5时,y=30. 在平面直角坐标系中, 先画出函数y = 2x 的
图象,然后探索y = 2x+3 的图象是什么样的图形,
猜测y = 2x+3的图象与y = 2x的图象有什么关系? 先取自变量x的一些值,算出y = 2x,y = 2x+3
对应的函数值,列成表格如下:y = 2x+3… -3 -2 -1 0 1 2 3 …… -6 -4 -2 0 2 4 6 …
… -3 -1 1 3 5 7 9 … 从上表可以看出,横坐标相同,y = 2x+3的
点的纵坐标比y = 2x的点的纵坐标大3,于是将
y = 2x的图象向上平移3 个单位,就得到y = 2x+3
的图象,如图4-11. 由于平移把直线变成与它平行的直线,因此
y = 2x+3的图象是与y = 2x平行的一条直线. 类似地,可以证明,一次函数y = kx+b的图
象是一条直线,它与正比例函数y = kx 的图象平
行,一次函数y = kx+b (k,b为常数,k≠0)的
图象可以看作由直线y = kx平移│b│个单位长度
而得到(当b>0时,向上平移; 当b<0时,向下平移). 由于两点确定一条直线,因此画一次函数的
图象,只要描出图象上的两个点,然后过这两点
作一条直线即可. 我们常常把这条直线叫作“直线
y = kx+b”.例3 画出一次函数y = -2x-3的图象.
在平面直角坐标系中描出两点A(0,-3),
B(1,-5),过这两点作直线,则这条直线是
一次函数y = -2x-3的图象,如图4-12. 观察画出的一次函数y = 2x+3 ,y = -2x-3的图象,
你能发现当自变量x的取值由小变大时,对应的函数
值如何变化吗? 一般地, 一次函数y = kx+b (k,b为常数,k≠0)具有如下性质:y = kx+bk > 0k < 0函数值y
的变化
函数值 y 随
自变量 x 的
增大而减小
函数值 y 随
自变量 x 的
增大而增大
例4 图4-13 描述了某一天小亮从家骑车去书店购书,
然后又骑车回家的情况. 你能说出小亮在路上的
情形吗?图4-13 第三段是与x 轴有交点的线段BC. 从横坐标看出,
小亮路上花了40min.当横坐标从60 变化到100 时,
纵坐标均匀减少,这说明小亮从书店出发匀速前进
40min,返回家中. 第二段是与x 轴平行的一条线段AB,当横坐标从30 变化到60时,纵坐标没有变化,这说明小亮在书店购书待了30min. 实际上,我们还可以比较第一段与第三段线段,
发现第一段更“陡”,这说明去书店的速度更快,
而回家的速度要慢一些.y = 3x-2y = -x结 束
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
