湘教版·2014-2015学年八年级数学下册精品课件:44用待定系数法确定一次函数表达式
文档属性
| 名称 | 湘教版·2014-2015学年八年级数学下册精品课件:44用待定系数法确定一次函数表达式 |  | |
| 格式 | zip | ||
| 文件大小 | 192.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 08:25:48 | ||
图片预览








文档简介
(共21张PPT)
用待定系数法确定
一次函数表达式
本课内容
本节内容
4.4
许多实际问题的解决都需要求出一次函数的
表达式. 怎样才能简便地求出一次函数的表达式呢?
如图4-14,已知一次函数的图象经过P(0,-1),
Q(1,1)两点. 怎样确定这个一次函数的表达式呢?
探究
图4-14
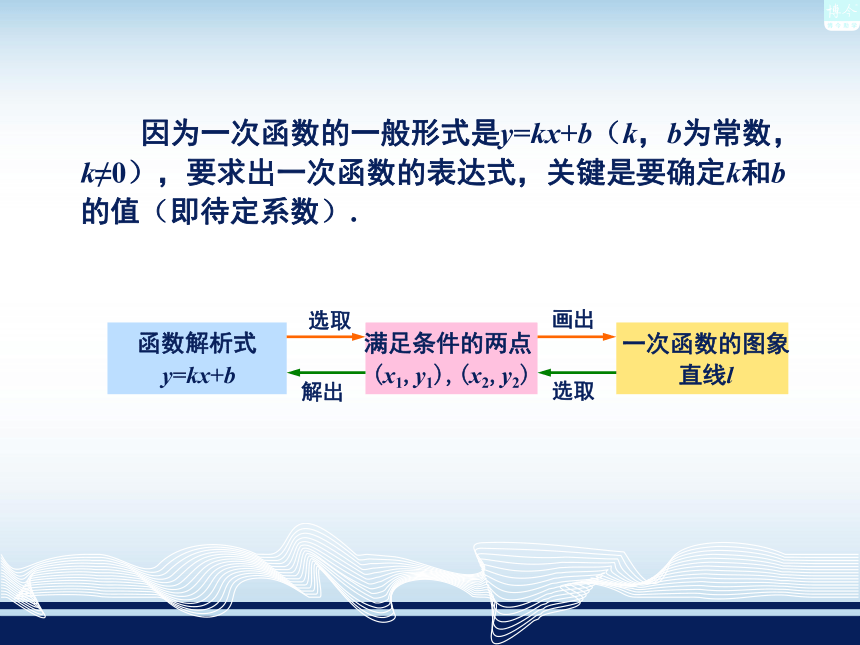
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象
直线l
选取
解出
画出
选取
因为P(0,-1) 和Q(1,1)都在该函数图象上,
因此它们的坐标应满足y=kx+b , 将这两点坐标代入该
式中,得到一个关于k,b的二元一次方程组:
k·0 + b = -1,
k + b = 1.
{
{
解这个方程组,得
k=2,
b=-1.
所以,这个一次函数的表达式为y = 2x- 1.
像这样,通过先设定函数表达式(确定函数模型),
再根据条件确定表达式中的未知系数,从而求出函数
的表达式的方法称为待定系数法.
议一议
议一议
议一议
议一议
议一议
议一议
要确定正比例函数的表达式需要几个条件?
举例和大家交流.
温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为
212℉;水的冰点温度是0℃,用华氏温度
度量为32 ℉.已知摄氏温度与华氏温度的关
近似地为一次函数关系,你能不能想出一个
办法方便地把华氏温度换算成摄氏温度?
例1
举
例
用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
解
由已知条件,得
212k + b =100,
32k + b = 0 .
{
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
在上述例子中,由于我们求出了摄氏温度与华氏温度的函数关系式,因此可以方便地把任何一个华氏温度换算成摄氏温度.
小提示
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图4-15所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
例2
举
例
图4-15
解这个方程组,得
所以 y = -5x + 40.
(1)求y关于x的函数表达式;
(1) 解
设一次函数的表达式为y = kx + b ,由于
点P (2,30), Q(6,10)都在一次
函数图象上,将这两点坐标代入表达式,得
2k + b =30,
6k + b =10.
{
(2)解 当剩余油量为0时, 即y=0 时,
有 -5x + 40 = 0,
解得 x = 8.
所以一箱油可供拖拉机工作8 h.
(2)一箱油可供拖拉机工作几小时?
练习
1. 把温度84华氏度换算成摄氏温度.
解
由摄氏温度与华氏温度的函数关系得
解得 C≈28.9(℃)
因此,把温度84华氏度换算成摄氏温度约为28.9度.
2. 已知一次函数的图象经过两点A(-1,3),B(2,-5),求这个函数的解析式.
解
设y=kx+b,由于两点A,B都在这个函数的图象上.
因此
-k + b = 3,
2k + b = -5.
因此所求一次函数的解析式为
解得 k= ,b= .
y = x + .
3. 酒精的体积随温度的升高而增大,体积与温度之间
在一定范围内近似于一次函数关系,现测得一定量
的酒精在0 ℃时的体积为5.250 L,在40 ℃时的体积
为5.481 L,求这些酒精在10 ℃和30 ℃时的体积各是
多少?
因此所求一次函数的解析式为 y=0.005775x+5.250.
解得 k=0.005775,b= 5.250 .
解
设体积与温度之间的函数关系为y=kx+b,由已知得:
k×0 + b = 5.250 ,
k×40 + b = 5.481.
在10 ℃,即x=10时,
体积y=0.005775×10 +5.250=5.30775(L).
在30 ℃,即x=30时,
体积y=0.005775×30 +5.250=5.42325(L).
答:这些酒精在10 ℃和30 ℃时的体积各是
5.30775L 和5.42325L.
中考 试题
例
百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分)之间的函数图象如图.根据图象回答下列问题:
(1)1.8分钟时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多
少时间到达?
(3)求乙队加速后,路程y(米)与时间x(分)之间的函数
关系式.
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分)
(1)(2)观察图象可得.(3)用待定系数法解.
分析
解
由图象可知,
(1)1.8分钟时甲龙舟队处于领先位置.
(2)在这次龙舟赛中,
乙龙舟队先到达终点,比甲提前0.5分钟.
(3)设乙队加速后,
y与x的关系式为:y=kx+b.
将(2,300)、(4.5,1050)分别代入上式,得
解得
∴ y = 300x-300(2≤x≤4.5)
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分)
结 束
用待定系数法确定
一次函数表达式
本课内容
本节内容
4.4
许多实际问题的解决都需要求出一次函数的
表达式. 怎样才能简便地求出一次函数的表达式呢?
如图4-14,已知一次函数的图象经过P(0,-1),
Q(1,1)两点. 怎样确定这个一次函数的表达式呢?
探究
图4-14
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象
直线l
选取
解出
画出
选取
因为P(0,-1) 和Q(1,1)都在该函数图象上,
因此它们的坐标应满足y=kx+b , 将这两点坐标代入该
式中,得到一个关于k,b的二元一次方程组:
k·0 + b = -1,
k + b = 1.
{
{
解这个方程组,得
k=2,
b=-1.
所以,这个一次函数的表达式为y = 2x- 1.
像这样,通过先设定函数表达式(确定函数模型),
再根据条件确定表达式中的未知系数,从而求出函数
的表达式的方法称为待定系数法.
议一议
议一议
议一议
议一议
议一议
议一议
要确定正比例函数的表达式需要几个条件?
举例和大家交流.
温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为
212℉;水的冰点温度是0℃,用华氏温度
度量为32 ℉.已知摄氏温度与华氏温度的关
近似地为一次函数关系,你能不能想出一个
办法方便地把华氏温度换算成摄氏温度?
例1
举
例
用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
解
由已知条件,得
212k + b =100,
32k + b = 0 .
{
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
在上述例子中,由于我们求出了摄氏温度与华氏温度的函数关系式,因此可以方便地把任何一个华氏温度换算成摄氏温度.
小提示
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图4-15所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
例2
举
例
图4-15
解这个方程组,得
所以 y = -5x + 40.
(1)求y关于x的函数表达式;
(1) 解
设一次函数的表达式为y = kx + b ,由于
点P (2,30), Q(6,10)都在一次
函数图象上,将这两点坐标代入表达式,得
2k + b =30,
6k + b =10.
{
(2)解 当剩余油量为0时, 即y=0 时,
有 -5x + 40 = 0,
解得 x = 8.
所以一箱油可供拖拉机工作8 h.
(2)一箱油可供拖拉机工作几小时?
练习
1. 把温度84华氏度换算成摄氏温度.
解
由摄氏温度与华氏温度的函数关系得
解得 C≈28.9(℃)
因此,把温度84华氏度换算成摄氏温度约为28.9度.
2. 已知一次函数的图象经过两点A(-1,3),B(2,-5),求这个函数的解析式.
解
设y=kx+b,由于两点A,B都在这个函数的图象上.
因此
-k + b = 3,
2k + b = -5.
因此所求一次函数的解析式为
解得 k= ,b= .
y = x + .
3. 酒精的体积随温度的升高而增大,体积与温度之间
在一定范围内近似于一次函数关系,现测得一定量
的酒精在0 ℃时的体积为5.250 L,在40 ℃时的体积
为5.481 L,求这些酒精在10 ℃和30 ℃时的体积各是
多少?
因此所求一次函数的解析式为 y=0.005775x+5.250.
解得 k=0.005775,b= 5.250 .
解
设体积与温度之间的函数关系为y=kx+b,由已知得:
k×0 + b = 5.250 ,
k×40 + b = 5.481.
在10 ℃,即x=10时,
体积y=0.005775×10 +5.250=5.30775(L).
在30 ℃,即x=30时,
体积y=0.005775×30 +5.250=5.42325(L).
答:这些酒精在10 ℃和30 ℃时的体积各是
5.30775L 和5.42325L.
中考 试题
例
百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分)之间的函数图象如图.根据图象回答下列问题:
(1)1.8分钟时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多
少时间到达?
(3)求乙队加速后,路程y(米)与时间x(分)之间的函数
关系式.
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分)
(1)(2)观察图象可得.(3)用待定系数法解.
分析
解
由图象可知,
(1)1.8分钟时甲龙舟队处于领先位置.
(2)在这次龙舟赛中,
乙龙舟队先到达终点,比甲提前0.5分钟.
(3)设乙队加速后,
y与x的关系式为:y=kx+b.
将(2,300)、(4.5,1050)分别代入上式,得
解得
∴ y = 300x-300(2≤x≤4.5)
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分)
结 束
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
