第7讲 动能定理 机械能守恒定律 能量守恒定律(含解析)2024年高考物理大二轮复习讲义
文档属性
| 名称 | 第7讲 动能定理 机械能守恒定律 能量守恒定律(含解析)2024年高考物理大二轮复习讲义 |  | |
| 格式 | docx | ||
| 文件大小 | 390.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-19 21:31:12 | ||
图片预览




文档简介
第7讲 动能定理 机械能守恒定律 能量守恒定律
目标要求
1.理解动能定理、机械能守恒定律、能量守恒定律。
2.会在具体问题中灵活选择合适的规律解决能量观点问题。
考点一 动能定理及应用
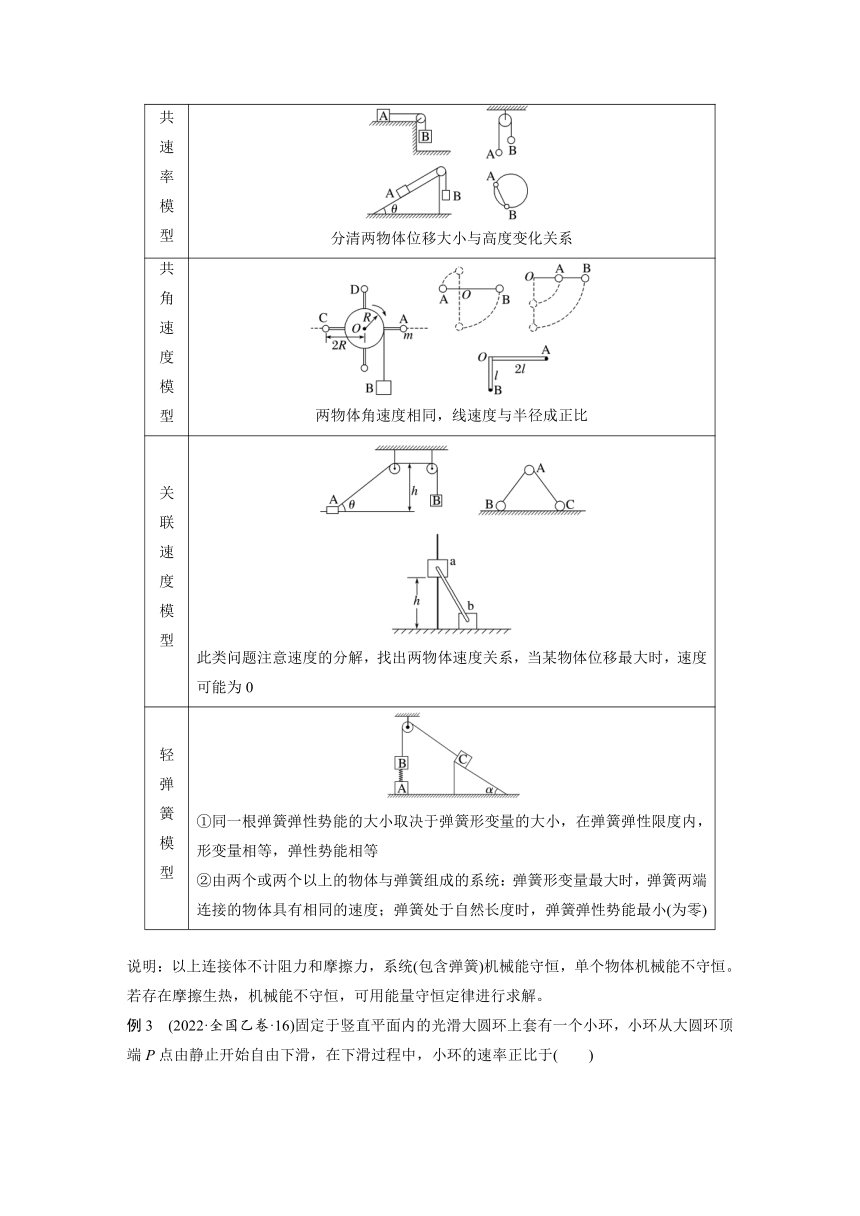
例1 (2021·山东卷·3)如图所示,粗糙程度处处相同的水平桌面上有一长为L的轻质细杆,一端可绕竖直光滑轴O转动,另一端与质量为m的小木块相连。木块以水平初速度v0出发,恰好能完成一个完整的圆周运动。在运动过程中,木块所受摩擦力的大小为( )
A. B. C. D.
学习笔记:______________________________________________________________
________________________________________________________________________
例2 (2022·浙江1月选考·20)如图所示,处于竖直平面内的一探究装置,由倾角α=37°的光滑直轨道AB、圆心为O1的半圆形光滑轨道BCD、圆心为O2的半圆形光滑细圆管轨道DEF、倾角也为37°的粗糙直轨道FG组成,B、D和F为轨道间的相切点,弹性板垂直轨道固定在G点(与B点等高),B、O1、D、O2和F点处于同一直线上。已知可视为质点的滑块质量m=0.1 kg,轨道BCD和DEF的半径R=0.15 m,轨道AB长度lAB=3 m,滑块与轨道FG间的动摩擦因数μ=,滑块与弹性板作用后,以等大速度弹回,sin 37°=0.6,cos 37°=0.8。滑块开始时均从轨道AB上某点静止释放。
(1)若释放点距B点的长度l=0.7 m,求滑块到最低点C时轨道对其支持力FN的大小;
(2)设释放点距B点的长度为lx,滑块第一次经F点时的速度v与lx之间的关系式;
(3)若滑块最终静止在轨道FG的中点,求释放点距B点长度lx的值。
________________________________________________________________________
________________________________________________________________________
1.应用动能定理解题的步骤图解:
2.应用动能定理的四点提醒:
(1)动能定理往往用于单个物体的运动过程,由于不涉及加速度和时间,比动力学方法要简捷。
(2)动能定理表达式是一个标量式,在某个方向上应用动能定理是没有依据的。
(3)物体在某个运动过程中包含几个运动性质不同的小过程(如加速、减速的过程),对全过程应用动能定理,往往能使问题简化。
(4)多过程往复运动问题一般应用动能定理求解。
考点二 机械能守恒定律及应用
1.判断物体或系统机械能是否守恒的三种方法
定义判断法 动能与势能之和不发生变化,系统机械能守恒
能量转化 判断法 没有与机械能以外的其他形式的能发生转化时,系统机械能守恒
做功判断法 只有重力或弹簧的弹力做功时,系统机械能守恒
2.机械能守恒定律的表达式
3.连接体的机械能守恒问题
共 速 率 模 型 分清两物体位移大小与高度变化关系
共 角 速 度 模 型 两物体角速度相同,线速度与半径成正比
关 联 速 度 模 型 此类问题注意速度的分解,找出两物体速度关系,当某物体位移最大时,速度可能为0
轻 弹 簧 模 型 ①同一根弹簧弹性势能的大小取决于弹簧形变量的大小,在弹簧弹性限度内,形变量相等,弹性势能相等 ②由两个或两个以上的物体与弹簧组成的系统:弹簧形变量最大时,弹簧两端连接的物体具有相同的速度;弹簧处于自然长度时,弹簧弹性势能最小(为零)
说明:以上连接体不计阻力和摩擦力,系统(包含弹簧)机械能守恒,单个物体机械能不守恒。若存在摩擦生热,机械能不守恒,可用能量守恒定律进行求解。
例3 (2022·全国乙卷·16)固定于竖直平面内的光滑大圆环上套有一个小环,小环从大圆环顶端P点由静止开始自由下滑,在下滑过程中,小环的速率正比于( )
A.它滑过的弧长
B.它下降的高度
C.它到P点的距离
D.它与P点的连线扫过的面积
学习笔记:______________________________________________________________
________________________________________________________________________
例4 (2023·江苏连云港市模拟)如图所示,竖直面内处于同一高度的光滑钉子M、N相距2L。带有光滑小孔的小球A穿过轻绳,轻绳的一端固定在钉子M上,另一端绕过钉子N与小球B相连,B球质量为m。用手将A球托住静止在M、N连线的中点P处,此时B球也处于静止状态。放手后,A球下落的最大距离为L,重力加速度为g,B球未运动到钉子N处。sin 53°=0.8,cos 53°=0.6,求:
(1)A球的质量mA;
(2)A球下落0.75L时的速度大小v。
________________________________________________________________________
________________________________________________________________________
考点三 能量守恒定律及应用
例5 如图所示,质量为2 000 kg的电梯的缆绳发生断裂后向下坠落,电梯刚接触井底缓冲弹簧时的速度为4 m/s,缓冲弹簧被压缩2 m时电梯停止了运动,下落过程中安全钳总共提供给电梯17 000 N的滑动摩擦力。已知弹簧的弹性势能为Ep=kx2(k为弹簧的劲度系数,x为弹簧的形变量),安全钳提供的滑动摩擦力等于最大静摩擦力,重力加速度g=10 m/s2,下列说法正确的是( )
A.弹簧的劲度系数为3 000 N/m
B.整个过程中电梯的加速度一直在减小
C.电梯停止在井底时受到的摩擦力大小为17 000 N
D.从电梯接触弹簧到速度最大的过程中电梯和弹簧组成的系统损失的机械能约为4 636 J
学习笔记:______________________________________________________________
________________________________________________________________________
例6 (2023·江苏盐城市、南京市期末)如图,一长L=6 m的倾斜传送带在电动机带动下以速度v=4 m/s沿顺时针方向匀速转动,传送带与水平方向的夹角θ=37°,质量m1=4 kg的小物块A和质量m2=2 kg的小物块B由跨过定滑轮的轻绳连接,A与定滑轮间的绳子与传送带平行,不可伸长的轻绳足够长。某时刻将物块A轻轻放在传送带底端,已知物块A与传送带间的动摩擦因数μ=0.5,不计滑轮的质量与摩擦,在A运动到传送带顶端前物块B都没有落地。取sin 37°=0.6,cos 37°=0.8,重力加速度g=10 m/s2。求:
(1)物块B刚下降时的加速度a的大小;
(2)物块A从底端到达顶端所需的时间t;
(3)物块A从底端到达顶端时,电动机多做的功W。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
传送带问题的综合分析
涉及物体在传送带上运动的具体细节问题,一般用动力学观点进行解决。传送带因传送物体多做的功,从能量的观点进行分析,等于物体增加的动能、重力势能及摩擦生热,而摩擦生热需要用摩擦力与相对路程的乘积进行求解。
1.如图所示,倾角为θ的斜面AB段光滑,BP段粗糙,一轻弹簧下端固定于斜面底端P处,弹簧处于原长时上端位于B点,可视为质点、质量为m的物体与BP之间的动摩擦因数为μ(μA.物体的最大动能等于mgxsin θ
B.弹簧的最大形变量大于x
C.物体第一次往返中克服摩擦力做的功为mgxsin θ
D.物体第二次沿斜面上升的最高位置在B点
2.北京冬奥会中的冰壶比赛令人印象深刻,冰壶比赛场地如图所示:运动员从起滑架处推着冰壶(可视为质点)沿中心线出发,在投掷线处放手让冰壶以一定的速度滑出,使冰壶的停止位置尽量靠近大本营圆心O,为了使冰壶滑行得更远,运动员可以用毛刷摩擦冰壶运行路径前方的冰面,使冰壶与冰面间的阻力减小。已知冰壶质量m=20 kg,未刷冰时,冰壶与冰面间的动摩擦因数μ1=0.02,刷冰后μ2=0.01,起滑架到投掷线的距离l1=10 m,投掷线与圆心O点的距离为l2=30 m,取g=10 m/s2,则:
(1)比赛中在不刷冰的情况下,要使冰壶刚好停在大本营圆心O处,求冰壶从投掷线被投出时速度v0大小;
(2)比赛中若冰壶从投掷线被投出时速度v1=3 m/s,为了使冰壶恰好停在圆心O处,求冰壶被投出后需要刷冰的距离s;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)运动员从起滑架处开始对冰壶施加一个沿中心线的水平推力F=20 N,推着冰壶由静止出发,冰壶到达投掷线之前就撤除推力,冰壶沿着中心线做匀减速直线运动,在不刷冰的情况下,最后停在圆心O处,求推力F的作用时间t。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
第7讲 动能定理 机械能
守恒定律 能量守恒定律
例1 B [在运动过程中,只有摩擦力做功,而摩擦力做功与路径有关,根据动能定理-Ff·2πL=0-mv02,可得摩擦力的大小Ff=,故选B。]
例2 (1)7 N (2)v=,其中lx≥0.85 m (3)见解析
解析 (1)滑块由静止释放到C点过程,由能量守恒定律有
mglsin 37°+mgR(1-cos 37°)=mvC2
在C点由牛顿第二定律有
FN-mg=m
解得FN=7 N
(2)要保证滑块能到F点,必须能过DEF的最高点,当滑块恰能达到最高点时,根据动能定理可得
mgl1sin 37°-(3mgRcos 37°+mgR)=0
解得l1=0.85 m
因此要能过F点必须满足lx≥0.85 m
能过最高点,则能到F点,根据动能定理可得
mglxsin 37°-4mgRcos 37°=mv2,
解得v=,其中lx≥0.85 m.
(3)设摩擦力做功为第一次到达中点时的n倍
mglxsin 37°-mgsin 37°-
nμmgcos 37°=0,
lFG=
解得lx= m(n=1,3,5,…)
又因为lAB≥lx≥0.85 m,lAB=3 m,
当n=1时,lx1= m
当n=3时,lx2= m
当n=5时,lx3= m。
例3 C [如图所示,
设小环下降的高度为h,大圆环的半径为R,小环到P点的距离为L,根据机械能守恒定律得mgh=mv2,
由几何关系可得h=Lsin θ,sin θ=,联立可得h=,则v=L,故C正确,A、B、D错误。]
例4 (1)m (2)
解析 (1)A球下落到最低点时,根据几何关系可得B上升的高度为
hB=2-2L=
根据A、B系统机械能守恒有mAghA=mghB
解得A球的质量mA=m
(2)A球下落0.75L时,设A球与M或N连线与竖直方向的夹角为θ,根据几何关系有tan θ==,解得θ=53°,根据几何关系可得B球上升高度为hB′=2-2L=0.5L,根据运动的合成与分解可得vB=2vcos 53°,根据系统机械能守恒,则有mAg×0.75L=mghB′+mAv2+mvB2,联立解得v=。
例5 D [电梯刚接触井底缓冲弹簧时的速度为4 m/s,缓冲弹簧被压缩2 m时电梯停止运动,根据能量守恒,得mv2+mg·Δx=k(Δx)2+Ff·Δx,代入数据解得k=11 000 N/m,故A错误;与弹簧接触前,电梯做匀加速直线运动,接触弹簧后,先做加速度逐渐减小的加速运动后做加速度逐渐增大的减速运动,故B错误;电梯停止在井底时,由受力平衡得kΔx=mg+Ff静,代入数据解得Ff静=kΔx-mg=22 000 N-20 000 N=2 000 N,故C错误;当电梯速度最大时,此时加速度为零,则kΔx′+Ff=mg,解得Δx′== m= m,从电梯接触弹簧到速度最大的过程中,电梯和弹簧组成的系统损失的机械能等于摩擦力做的负功,则ΔE=Ff·Δx′=17 000× J≈4 636 J,故D正确。]
例6 (1)2 m/s2 (2)2.5 s (3)136 J
解析 (1)对A分析FT+μm1gcos θ-m1gsin θ=m1a
对B分析m2g-FT=m2a
解得a=2 m/s2
(2)当A达到与传送带共速所用时间t1==2 s
A的位移x1=t1=4 m
之后匀速,时间t2==0.5 s
物块A从底端到达顶端所需的时间t=t1+t2=2.5 s
(3)物块A从底端到达顶端时,与传送带的相对位移Δx=vt1-x1=4 m
根据能量守恒得W+m2gL-m1gLsin θ=(m1+m2)v2+μm1gΔxcos θ
解得W=136 J。
高考预测
1.C [物体接触弹簧前,由机械能守恒定律可知,物体刚接触弹簧时的动能为Ek=mgxsin θ,物体接触弹簧后,重力沿斜面向下的分力先大于滑动摩擦力和弹簧弹力的合力,物体先加速下滑,后来重力沿斜面向下的分力小于滑动摩擦力和弹簧弹力的合力,物体减速下滑,所以当重力沿斜面向下的分力等于滑动摩擦力和弹簧弹力的合力时物体所受的合力为零,速度最大,动能最大,所以物体的最大动能一定大于mgxsin θ,A错误;设弹簧的最大压缩量为L,弹性势能最大为Ep,物体从A到最低点的过程,由能量守恒定律得mg(L+x)sin θ=μmgLcos θ+Ep,物体从最低点到Q点的过程,由能量守恒定律得mg(L+)sin θ+μmgLcos θ=Ep,联立解得L=,由于μ2.(1)2 m/s (2)15 m (3)2 s
解析 (1)研究冰壶运动过程,根据位移与速度关系得v02=2a1l2
a1=μ1g
解得v0=2 m/s
(2)研究冰壶的运动过程,根据动能定理得
-μ1mg(l2-s)-μ2mgs=0-mv12
解得s=15 m
(3)研究冰壶运动全程,根据动能定理得Fl-μ1mg(l1+l2)=0
又F-μ1mg=ma
l=at2
解得t=2 s。
目标要求
1.理解动能定理、机械能守恒定律、能量守恒定律。
2.会在具体问题中灵活选择合适的规律解决能量观点问题。
考点一 动能定理及应用
例1 (2021·山东卷·3)如图所示,粗糙程度处处相同的水平桌面上有一长为L的轻质细杆,一端可绕竖直光滑轴O转动,另一端与质量为m的小木块相连。木块以水平初速度v0出发,恰好能完成一个完整的圆周运动。在运动过程中,木块所受摩擦力的大小为( )
A. B. C. D.
学习笔记:______________________________________________________________
________________________________________________________________________
例2 (2022·浙江1月选考·20)如图所示,处于竖直平面内的一探究装置,由倾角α=37°的光滑直轨道AB、圆心为O1的半圆形光滑轨道BCD、圆心为O2的半圆形光滑细圆管轨道DEF、倾角也为37°的粗糙直轨道FG组成,B、D和F为轨道间的相切点,弹性板垂直轨道固定在G点(与B点等高),B、O1、D、O2和F点处于同一直线上。已知可视为质点的滑块质量m=0.1 kg,轨道BCD和DEF的半径R=0.15 m,轨道AB长度lAB=3 m,滑块与轨道FG间的动摩擦因数μ=,滑块与弹性板作用后,以等大速度弹回,sin 37°=0.6,cos 37°=0.8。滑块开始时均从轨道AB上某点静止释放。
(1)若释放点距B点的长度l=0.7 m,求滑块到最低点C时轨道对其支持力FN的大小;
(2)设释放点距B点的长度为lx,滑块第一次经F点时的速度v与lx之间的关系式;
(3)若滑块最终静止在轨道FG的中点,求释放点距B点长度lx的值。
________________________________________________________________________
________________________________________________________________________
1.应用动能定理解题的步骤图解:
2.应用动能定理的四点提醒:
(1)动能定理往往用于单个物体的运动过程,由于不涉及加速度和时间,比动力学方法要简捷。
(2)动能定理表达式是一个标量式,在某个方向上应用动能定理是没有依据的。
(3)物体在某个运动过程中包含几个运动性质不同的小过程(如加速、减速的过程),对全过程应用动能定理,往往能使问题简化。
(4)多过程往复运动问题一般应用动能定理求解。
考点二 机械能守恒定律及应用
1.判断物体或系统机械能是否守恒的三种方法
定义判断法 动能与势能之和不发生变化,系统机械能守恒
能量转化 判断法 没有与机械能以外的其他形式的能发生转化时,系统机械能守恒
做功判断法 只有重力或弹簧的弹力做功时,系统机械能守恒
2.机械能守恒定律的表达式
3.连接体的机械能守恒问题
共 速 率 模 型 分清两物体位移大小与高度变化关系
共 角 速 度 模 型 两物体角速度相同,线速度与半径成正比
关 联 速 度 模 型 此类问题注意速度的分解,找出两物体速度关系,当某物体位移最大时,速度可能为0
轻 弹 簧 模 型 ①同一根弹簧弹性势能的大小取决于弹簧形变量的大小,在弹簧弹性限度内,形变量相等,弹性势能相等 ②由两个或两个以上的物体与弹簧组成的系统:弹簧形变量最大时,弹簧两端连接的物体具有相同的速度;弹簧处于自然长度时,弹簧弹性势能最小(为零)
说明:以上连接体不计阻力和摩擦力,系统(包含弹簧)机械能守恒,单个物体机械能不守恒。若存在摩擦生热,机械能不守恒,可用能量守恒定律进行求解。
例3 (2022·全国乙卷·16)固定于竖直平面内的光滑大圆环上套有一个小环,小环从大圆环顶端P点由静止开始自由下滑,在下滑过程中,小环的速率正比于( )
A.它滑过的弧长
B.它下降的高度
C.它到P点的距离
D.它与P点的连线扫过的面积
学习笔记:______________________________________________________________
________________________________________________________________________
例4 (2023·江苏连云港市模拟)如图所示,竖直面内处于同一高度的光滑钉子M、N相距2L。带有光滑小孔的小球A穿过轻绳,轻绳的一端固定在钉子M上,另一端绕过钉子N与小球B相连,B球质量为m。用手将A球托住静止在M、N连线的中点P处,此时B球也处于静止状态。放手后,A球下落的最大距离为L,重力加速度为g,B球未运动到钉子N处。sin 53°=0.8,cos 53°=0.6,求:
(1)A球的质量mA;
(2)A球下落0.75L时的速度大小v。
________________________________________________________________________
________________________________________________________________________
考点三 能量守恒定律及应用
例5 如图所示,质量为2 000 kg的电梯的缆绳发生断裂后向下坠落,电梯刚接触井底缓冲弹簧时的速度为4 m/s,缓冲弹簧被压缩2 m时电梯停止了运动,下落过程中安全钳总共提供给电梯17 000 N的滑动摩擦力。已知弹簧的弹性势能为Ep=kx2(k为弹簧的劲度系数,x为弹簧的形变量),安全钳提供的滑动摩擦力等于最大静摩擦力,重力加速度g=10 m/s2,下列说法正确的是( )
A.弹簧的劲度系数为3 000 N/m
B.整个过程中电梯的加速度一直在减小
C.电梯停止在井底时受到的摩擦力大小为17 000 N
D.从电梯接触弹簧到速度最大的过程中电梯和弹簧组成的系统损失的机械能约为4 636 J
学习笔记:______________________________________________________________
________________________________________________________________________
例6 (2023·江苏盐城市、南京市期末)如图,一长L=6 m的倾斜传送带在电动机带动下以速度v=4 m/s沿顺时针方向匀速转动,传送带与水平方向的夹角θ=37°,质量m1=4 kg的小物块A和质量m2=2 kg的小物块B由跨过定滑轮的轻绳连接,A与定滑轮间的绳子与传送带平行,不可伸长的轻绳足够长。某时刻将物块A轻轻放在传送带底端,已知物块A与传送带间的动摩擦因数μ=0.5,不计滑轮的质量与摩擦,在A运动到传送带顶端前物块B都没有落地。取sin 37°=0.6,cos 37°=0.8,重力加速度g=10 m/s2。求:
(1)物块B刚下降时的加速度a的大小;
(2)物块A从底端到达顶端所需的时间t;
(3)物块A从底端到达顶端时,电动机多做的功W。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
传送带问题的综合分析
涉及物体在传送带上运动的具体细节问题,一般用动力学观点进行解决。传送带因传送物体多做的功,从能量的观点进行分析,等于物体增加的动能、重力势能及摩擦生热,而摩擦生热需要用摩擦力与相对路程的乘积进行求解。
1.如图所示,倾角为θ的斜面AB段光滑,BP段粗糙,一轻弹簧下端固定于斜面底端P处,弹簧处于原长时上端位于B点,可视为质点、质量为m的物体与BP之间的动摩擦因数为μ(μ
B.弹簧的最大形变量大于x
C.物体第一次往返中克服摩擦力做的功为mgxsin θ
D.物体第二次沿斜面上升的最高位置在B点
2.北京冬奥会中的冰壶比赛令人印象深刻,冰壶比赛场地如图所示:运动员从起滑架处推着冰壶(可视为质点)沿中心线出发,在投掷线处放手让冰壶以一定的速度滑出,使冰壶的停止位置尽量靠近大本营圆心O,为了使冰壶滑行得更远,运动员可以用毛刷摩擦冰壶运行路径前方的冰面,使冰壶与冰面间的阻力减小。已知冰壶质量m=20 kg,未刷冰时,冰壶与冰面间的动摩擦因数μ1=0.02,刷冰后μ2=0.01,起滑架到投掷线的距离l1=10 m,投掷线与圆心O点的距离为l2=30 m,取g=10 m/s2,则:
(1)比赛中在不刷冰的情况下,要使冰壶刚好停在大本营圆心O处,求冰壶从投掷线被投出时速度v0大小;
(2)比赛中若冰壶从投掷线被投出时速度v1=3 m/s,为了使冰壶恰好停在圆心O处,求冰壶被投出后需要刷冰的距离s;
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
(3)运动员从起滑架处开始对冰壶施加一个沿中心线的水平推力F=20 N,推着冰壶由静止出发,冰壶到达投掷线之前就撤除推力,冰壶沿着中心线做匀减速直线运动,在不刷冰的情况下,最后停在圆心O处,求推力F的作用时间t。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
第7讲 动能定理 机械能
守恒定律 能量守恒定律
例1 B [在运动过程中,只有摩擦力做功,而摩擦力做功与路径有关,根据动能定理-Ff·2πL=0-mv02,可得摩擦力的大小Ff=,故选B。]
例2 (1)7 N (2)v=,其中lx≥0.85 m (3)见解析
解析 (1)滑块由静止释放到C点过程,由能量守恒定律有
mglsin 37°+mgR(1-cos 37°)=mvC2
在C点由牛顿第二定律有
FN-mg=m
解得FN=7 N
(2)要保证滑块能到F点,必须能过DEF的最高点,当滑块恰能达到最高点时,根据动能定理可得
mgl1sin 37°-(3mgRcos 37°+mgR)=0
解得l1=0.85 m
因此要能过F点必须满足lx≥0.85 m
能过最高点,则能到F点,根据动能定理可得
mglxsin 37°-4mgRcos 37°=mv2,
解得v=,其中lx≥0.85 m.
(3)设摩擦力做功为第一次到达中点时的n倍
mglxsin 37°-mgsin 37°-
nμmgcos 37°=0,
lFG=
解得lx= m(n=1,3,5,…)
又因为lAB≥lx≥0.85 m,lAB=3 m,
当n=1时,lx1= m
当n=3时,lx2= m
当n=5时,lx3= m。
例3 C [如图所示,
设小环下降的高度为h,大圆环的半径为R,小环到P点的距离为L,根据机械能守恒定律得mgh=mv2,
由几何关系可得h=Lsin θ,sin θ=,联立可得h=,则v=L,故C正确,A、B、D错误。]
例4 (1)m (2)
解析 (1)A球下落到最低点时,根据几何关系可得B上升的高度为
hB=2-2L=
根据A、B系统机械能守恒有mAghA=mghB
解得A球的质量mA=m
(2)A球下落0.75L时,设A球与M或N连线与竖直方向的夹角为θ,根据几何关系有tan θ==,解得θ=53°,根据几何关系可得B球上升高度为hB′=2-2L=0.5L,根据运动的合成与分解可得vB=2vcos 53°,根据系统机械能守恒,则有mAg×0.75L=mghB′+mAv2+mvB2,联立解得v=。
例5 D [电梯刚接触井底缓冲弹簧时的速度为4 m/s,缓冲弹簧被压缩2 m时电梯停止运动,根据能量守恒,得mv2+mg·Δx=k(Δx)2+Ff·Δx,代入数据解得k=11 000 N/m,故A错误;与弹簧接触前,电梯做匀加速直线运动,接触弹簧后,先做加速度逐渐减小的加速运动后做加速度逐渐增大的减速运动,故B错误;电梯停止在井底时,由受力平衡得kΔx=mg+Ff静,代入数据解得Ff静=kΔx-mg=22 000 N-20 000 N=2 000 N,故C错误;当电梯速度最大时,此时加速度为零,则kΔx′+Ff=mg,解得Δx′== m= m,从电梯接触弹簧到速度最大的过程中,电梯和弹簧组成的系统损失的机械能等于摩擦力做的负功,则ΔE=Ff·Δx′=17 000× J≈4 636 J,故D正确。]
例6 (1)2 m/s2 (2)2.5 s (3)136 J
解析 (1)对A分析FT+μm1gcos θ-m1gsin θ=m1a
对B分析m2g-FT=m2a
解得a=2 m/s2
(2)当A达到与传送带共速所用时间t1==2 s
A的位移x1=t1=4 m
之后匀速,时间t2==0.5 s
物块A从底端到达顶端所需的时间t=t1+t2=2.5 s
(3)物块A从底端到达顶端时,与传送带的相对位移Δx=vt1-x1=4 m
根据能量守恒得W+m2gL-m1gLsin θ=(m1+m2)v2+μm1gΔxcos θ
解得W=136 J。
高考预测
1.C [物体接触弹簧前,由机械能守恒定律可知,物体刚接触弹簧时的动能为Ek=mgxsin θ,物体接触弹簧后,重力沿斜面向下的分力先大于滑动摩擦力和弹簧弹力的合力,物体先加速下滑,后来重力沿斜面向下的分力小于滑动摩擦力和弹簧弹力的合力,物体减速下滑,所以当重力沿斜面向下的分力等于滑动摩擦力和弹簧弹力的合力时物体所受的合力为零,速度最大,动能最大,所以物体的最大动能一定大于mgxsin θ,A错误;设弹簧的最大压缩量为L,弹性势能最大为Ep,物体从A到最低点的过程,由能量守恒定律得mg(L+x)sin θ=μmgLcos θ+Ep,物体从最低点到Q点的过程,由能量守恒定律得mg(L+)sin θ+μmgLcos θ=Ep,联立解得L=,由于μ
解析 (1)研究冰壶运动过程,根据位移与速度关系得v02=2a1l2
a1=μ1g
解得v0=2 m/s
(2)研究冰壶的运动过程,根据动能定理得
-μ1mg(l2-s)-μ2mgs=0-mv12
解得s=15 m
(3)研究冰壶运动全程,根据动能定理得Fl-μ1mg(l1+l2)=0
又F-μ1mg=ma
l=at2
解得t=2 s。
同课章节目录
