数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式 说课(共28张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式 说课(共28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:01:15 | ||
图片预览








文档简介
(共28张PPT)
点到直线的距离公式
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
选自2019人教版A版普通高中数学选择性必修第一册第二章第三节
教材分析
一、教材分析
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
点到直线的距离公式是高中解析几何课程中最重要的也是最精彩的公式之一,它是解决点线、线线距离的基础,也是研究直线与圆、圆与圆位置关系的重要工具,同时为后面学习圆锥曲线作准备.
教材试图让学生通过学习、探究点到直线的距离公式的思维过程,深刻领会蕴涵于其中的数学思想和方法,逐步学会利用数形结合、算法、转化、向量等数学思想方法来解决数学问题;能让学生充分体验作为学习主体进行探究、发现和创造的乐趣.
从学生的认知基础看,学生对点、线的几何和代数表示以及两点间距离公式都很熟悉,本节课利用所学知识进行公式推导,其运算或繁琐或难度较大,但公式推广应用比较简单,其中包含的运算能力是解析几何学习中学生尤其需要掌握的核心素养,所以让学生参与数学公式推理的建构过程,调动学生积极探索公式的形成显得尤为重要.
二、学情分析
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
三、教学目标
1.理解点到直线距离公式的推导过程,掌握点到直线的距离公式及简单应用;
2.经历点到直线距离公式的探索过程;体会推导过程中蕴含的数形结合、分类讨论、化归转化等数学思想,发展学生数学抽象、逻辑推理、数学运算等核心素养;
3.通过探索公式的推导过程,培养学生的意志品质;感受数学公式的简洁美。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
四、教学重难点
重点
点到直线距离公式及其应用
难点
点到直线距离公式的推导.包含选择解决问题的策略,化繁为简的计算方法;“设而不求”的解析几何运算策略,方程组的演化。联系立体几何中,求点到面距离的办法引导出学生借助向量解决距离问题的策略。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
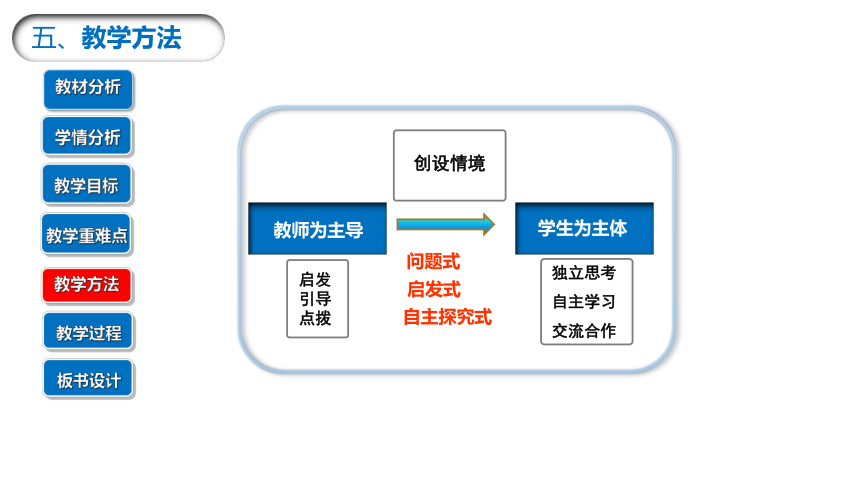
五、教学方法
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
学生为主体
创设情境
教师为主导
启发引导点拨
独立思考
自主学习
交流合作
启发式
自主探究式
问题式
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
4
典例剖析、巩固提升
3
探究新知,得出一般性的公式
2
从特殊到一般(求点到直线的距离)
5
归纳总结
1
小视频创设情境
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
1
小视频创设情境
沙漠喝水选择线路,垂直路线最短,引出本节课的主题。
设计意图:通过趣味数学问题,
引出在坐标系下探究点到直线距离
的问题。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
2
从特殊到一般(求点到直线的距离)
x0
y0
|y0|
|x0|
x
y
P0 (x0,y0)
O
|x1-x0|
|y1-y0|
问题:
点 到 x 轴, y 轴的距离?
点 到直线 x =x1, 直线 y =y1的距离?
设计意图:引例1,由点到特殊直线距离,
总结出点到垂直于坐标轴直线的距离通法。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
直接法
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
等面积法
设计意图:引例2,学生说解题思路,
一是让学生清晰有条理的表达自己的思考
过程;
二是其求解过程提示了接下来推导的途径。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
问题3 能否推导出一般化的公式来求点到直线的距离呢?
(先考虑与坐标轴不垂直时)已知点P0(x0,y0),
直线l: Ax+By+C=0( A≠0且B≠0 ), 如何求点P0到直线l的距离?
3
探究新知,得出一般性的公式
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
思路一:直接法
直线l的方程
直线 l 的方程
直线PQ的方程
交点
直线PQ的斜率
点P的坐标
点Q的坐标
两点间距离公式
直线l的斜率
l⊥PQ
点P、Q之间的距离|PQ |( P到l 的距离)
x
y
O
Q
P
探究新知
x
y
O
Q
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
x
y
P0 (x0,y0)
O
d=
d=
当直线l: Ax+By+C=0与坐标轴垂直即:
(1)当A=0时,且B≠0时,方程化为:
(2)当B=0时,且A≠0时,方程化为:
验证直线与坐标轴垂直的情况
设计意图:以上推导培养学生严谨,
周密的推理能力,得到一般性
结论,形成完整的数学模型,感受
数学的严谨性和数学结论的确定性,
形成科学的态度。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
(1)方法:根据点到直线距离的定义,
将点到直线距离转化为两点之间的距离.
(2)缺点:思路自然但运算量较大.
(3)思考:仔细观察求解过程, 思考引起复杂运算
的原因是什么
(4)对策:由此能否给出简化运算的方法
能否不求点Q的坐标?
追问4:能否从方程组中直接求出 ?
推导过程的感受
探究新知
①
②
③
④
③式的平方+
④式的平方得:
“整体代换”
“设而不求”
在上述方法中,若设垂足Q的坐标(x,y),则
结合方程组 我们能直接求出 ,进而
求出 .
改进:用设而不求法推导
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
思路二:间接法(等面积法)
x
y
O
S
R
l
Q
面积法求出|PQ|
求出|PR|
求出|PS|
利用勾股定理求出|RS|
求出点R的坐标
求出点S的坐标
P
探究新知
P
思路二:间接法(等面积法)
这个方法在A≠0且B≠0的前提下推导的。
x
y
O
S
R
l
Q
六、教学过程
l的一个方向向量为
所以与l的方向向量垂直的向量取
因为点M在直线上,所以Ax+By+C=0,所以Ax+By=-C,代入上式得
因此|PQ|=
从而
思路三:向量投影法
回忆立体几何中的点到面的距离的公式:
我们知道,向量是解决距离、角度问题的有力工具,能否用向量的方法求点到直线的距离?
M(x,y)
x
y
O
P
n
类比,点P到直线l的距离,就是 的模。
模即是 在 l 垂直方向上的投影绝对值。
α
A
l
Q
P
d
向量法避开了求Q点坐标和
求|PQ|的过程。直线与坐标
轴垂直时也适用。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
得出公式:
1.用此公式时直线方程必须先化成一般式
2.当A=0或B=0时,此公式也成立;
注:
3.当P点在直线上时,上式分子为零,此公式也成立;
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
备选思路:(1)直角三角形角中内角与倾斜角的关系
作PR平行于x轴与直线相交于R,
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
备选思路:(2)直角三角形角中内角与倾斜角的关系
y
O
S
Q
P
M
1
N
T
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
备选思路:(3)距离问题转化成二次函数最值问题
在直线上任取一点
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
1.求点A(-2,3)到直线3x+4y+3=0的距离.
课堂练习
3.求点P(-1,2)到直线3y=2的距离.
4
典例剖析、巩固提升
2.求点P(1,0)到直线 的距离.
4.你能说出代数式 的几何意义吗
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
点 到直线 的距离公式:
我们尝试了三种研究点到直线距离的方法。
第一,直接找进垂足求两点间距离,优点是思路自然,缺点是计算量大。
第二,优化解法,通过设而不求,从方程组中演化出两点间距离公式, 体会到数学运算的巧妙。
第三,通过复习上一章点到平面距离向量方法,同学们形成了用向量解决点到直线的距离,方法自然,计算量也小。 是同学们体会数学方法的灵活性和多角度。体会数学知识间的联系。
5
归纳总结
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
七、板书设计
标题:点到直线的距离公式
1.点到直线的距离定义:
2.点到直线的距离公式推导
推导过程
3.例题
解答过程
4.课堂练习
解答过程
点到直线的距离公式
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
选自2019人教版A版普通高中数学选择性必修第一册第二章第三节
教材分析
一、教材分析
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
点到直线的距离公式是高中解析几何课程中最重要的也是最精彩的公式之一,它是解决点线、线线距离的基础,也是研究直线与圆、圆与圆位置关系的重要工具,同时为后面学习圆锥曲线作准备.
教材试图让学生通过学习、探究点到直线的距离公式的思维过程,深刻领会蕴涵于其中的数学思想和方法,逐步学会利用数形结合、算法、转化、向量等数学思想方法来解决数学问题;能让学生充分体验作为学习主体进行探究、发现和创造的乐趣.
从学生的认知基础看,学生对点、线的几何和代数表示以及两点间距离公式都很熟悉,本节课利用所学知识进行公式推导,其运算或繁琐或难度较大,但公式推广应用比较简单,其中包含的运算能力是解析几何学习中学生尤其需要掌握的核心素养,所以让学生参与数学公式推理的建构过程,调动学生积极探索公式的形成显得尤为重要.
二、学情分析
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
三、教学目标
1.理解点到直线距离公式的推导过程,掌握点到直线的距离公式及简单应用;
2.经历点到直线距离公式的探索过程;体会推导过程中蕴含的数形结合、分类讨论、化归转化等数学思想,发展学生数学抽象、逻辑推理、数学运算等核心素养;
3.通过探索公式的推导过程,培养学生的意志品质;感受数学公式的简洁美。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
四、教学重难点
重点
点到直线距离公式及其应用
难点
点到直线距离公式的推导.包含选择解决问题的策略,化繁为简的计算方法;“设而不求”的解析几何运算策略,方程组的演化。联系立体几何中,求点到面距离的办法引导出学生借助向量解决距离问题的策略。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
五、教学方法
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
学生为主体
创设情境
教师为主导
启发引导点拨
独立思考
自主学习
交流合作
启发式
自主探究式
问题式
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
4
典例剖析、巩固提升
3
探究新知,得出一般性的公式
2
从特殊到一般(求点到直线的距离)
5
归纳总结
1
小视频创设情境
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
1
小视频创设情境
沙漠喝水选择线路,垂直路线最短,引出本节课的主题。
设计意图:通过趣味数学问题,
引出在坐标系下探究点到直线距离
的问题。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
2
从特殊到一般(求点到直线的距离)
x0
y0
|y0|
|x0|
x
y
P0 (x0,y0)
O
|x1-x0|
|y1-y0|
问题:
点 到 x 轴, y 轴的距离?
点 到直线 x =x1, 直线 y =y1的距离?
设计意图:引例1,由点到特殊直线距离,
总结出点到垂直于坐标轴直线的距离通法。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
直接法
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
等面积法
设计意图:引例2,学生说解题思路,
一是让学生清晰有条理的表达自己的思考
过程;
二是其求解过程提示了接下来推导的途径。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
问题3 能否推导出一般化的公式来求点到直线的距离呢?
(先考虑与坐标轴不垂直时)已知点P0(x0,y0),
直线l: Ax+By+C=0( A≠0且B≠0 ), 如何求点P0到直线l的距离?
3
探究新知,得出一般性的公式
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
思路一:直接法
直线l的方程
直线 l 的方程
直线PQ的方程
交点
直线PQ的斜率
点P的坐标
点Q的坐标
两点间距离公式
直线l的斜率
l⊥PQ
点P、Q之间的距离|PQ |( P到l 的距离)
x
y
O
Q
P
探究新知
x
y
O
Q
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
x
y
P0 (x0,y0)
O
d=
d=
当直线l: Ax+By+C=0与坐标轴垂直即:
(1)当A=0时,且B≠0时,方程化为:
(2)当B=0时,且A≠0时,方程化为:
验证直线与坐标轴垂直的情况
设计意图:以上推导培养学生严谨,
周密的推理能力,得到一般性
结论,形成完整的数学模型,感受
数学的严谨性和数学结论的确定性,
形成科学的态度。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
(1)方法:根据点到直线距离的定义,
将点到直线距离转化为两点之间的距离.
(2)缺点:思路自然但运算量较大.
(3)思考:仔细观察求解过程, 思考引起复杂运算
的原因是什么
(4)对策:由此能否给出简化运算的方法
能否不求点Q的坐标?
追问4:能否从方程组中直接求出 ?
推导过程的感受
探究新知
①
②
③
④
③式的平方+
④式的平方得:
“整体代换”
“设而不求”
在上述方法中,若设垂足Q的坐标(x,y),则
结合方程组 我们能直接求出 ,进而
求出 .
改进:用设而不求法推导
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
思路二:间接法(等面积法)
x
y
O
S
R
l
Q
面积法求出|PQ|
求出|PR|
求出|PS|
利用勾股定理求出|RS|
求出点R的坐标
求出点S的坐标
P
探究新知
P
思路二:间接法(等面积法)
这个方法在A≠0且B≠0的前提下推导的。
x
y
O
S
R
l
Q
六、教学过程
l的一个方向向量为
所以与l的方向向量垂直的向量取
因为点M在直线上,所以Ax+By+C=0,所以Ax+By=-C,代入上式得
因此|PQ|=
从而
思路三:向量投影法
回忆立体几何中的点到面的距离的公式:
我们知道,向量是解决距离、角度问题的有力工具,能否用向量的方法求点到直线的距离?
M(x,y)
x
y
O
P
n
类比,点P到直线l的距离,就是 的模。
模即是 在 l 垂直方向上的投影绝对值。
α
A
l
Q
P
d
向量法避开了求Q点坐标和
求|PQ|的过程。直线与坐标
轴垂直时也适用。
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
得出公式:
1.用此公式时直线方程必须先化成一般式
2.当A=0或B=0时,此公式也成立;
注:
3.当P点在直线上时,上式分子为零,此公式也成立;
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
备选思路:(1)直角三角形角中内角与倾斜角的关系
作PR平行于x轴与直线相交于R,
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
备选思路:(2)直角三角形角中内角与倾斜角的关系
y
O
S
Q
P
M
1
N
T
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
备选思路:(3)距离问题转化成二次函数最值问题
在直线上任取一点
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
1.求点A(-2,3)到直线3x+4y+3=0的距离.
课堂练习
3.求点P(-1,2)到直线3y=2的距离.
4
典例剖析、巩固提升
2.求点P(1,0)到直线 的距离.
4.你能说出代数式 的几何意义吗
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
六、教学过程
点 到直线 的距离公式:
我们尝试了三种研究点到直线距离的方法。
第一,直接找进垂足求两点间距离,优点是思路自然,缺点是计算量大。
第二,优化解法,通过设而不求,从方程组中演化出两点间距离公式, 体会到数学运算的巧妙。
第三,通过复习上一章点到平面距离向量方法,同学们形成了用向量解决点到直线的距离,方法自然,计算量也小。 是同学们体会数学方法的灵活性和多角度。体会数学知识间的联系。
5
归纳总结
学情分析
教学目标
教学重难点
教学方法
教学过程
板书设计
教材分析
七、板书设计
标题:点到直线的距离公式
1.点到直线的距离定义:
2.点到直线的距离公式推导
推导过程
3.例题
解答过程
4.课堂练习
解答过程
