幂函数(广东省广州市东山区)
图片预览







文档简介
课件24张PPT。幂函数数学的内在美常常让我们深深感动欣赏运算的完美性: 我们来看看由8、2、3、 这四个数,运用数学符号可组成哪些等式?函数的完美追求我们知道在指数式1、如果a一定,N随b的变化而变化,我们建立了指
数函数2、如果a一定, b 随N的变化而变化,我们建立了
对数函数设想:如果b一定, N随a的变化而变化,是不是也应该可以确定了一个函数呢?函数的生活实例问题1:如果张红购买了每千克1元的蔬菜w千克,那么她
需要付的钱数 元,
问题2:如果正方形的边长为a,那么正方形的面积
是 ,
问题3:如果正方体的边长为a,那么正方体的体积是
问题4:如果一个正方形场地的面积为S,那么这个正方形的边长
,
问题5:如果某人t s内骑车行进了1km,那么他骑车的平均速度
V=t?1 km/s
PwSay=xy=x2y=x3y=x-1P=W____是____的函数____是____的函数V是a的函数a是S的函数V是t 的函数S=a2V=a3以上问题中的函数有什么共同特征?(1)都是函数;
(2)均是以自变量为底的幂;
(3)指数为常数;
(4)幂前的系数也为1。
上述问题中涉及的函数,都是形如
的函数幂函数的一般概念: 一般地,函数
幂函数的结构特征
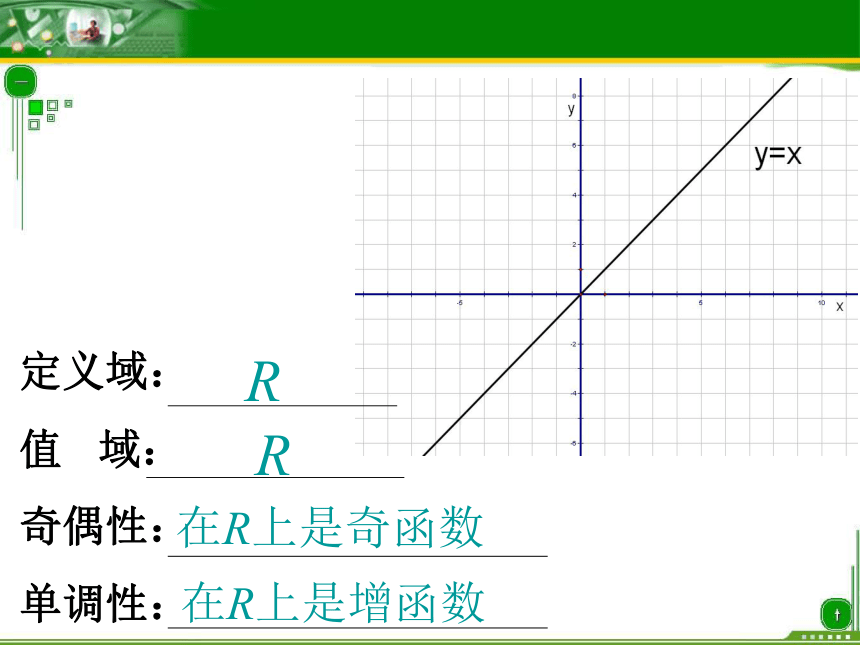
你能说出幂函数与指数函数的区别吗?3. 幂前的系数也为11.自变量为底2.指数为常数叫做幂函数,其中x为自变量,a为常数。试判断下列函数是不是幂函数下面研究幂函数 研究图象的性质,一般包括:定义域、值域、单调性、奇偶性、过定点的情况等研究 。函数图象的画法是:列表描点连线奇偶
奇非奇
非偶奇RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,几个幂函数的性质在R上增在[0,+∞)
上增,在(-∞,0]上
减,在[0,+∞)上
增,在(0,+∞)
上减在第一象限内,函数图象的变化趋势与指数有什么关系?
y=x3a > 0a < 0
(1)图象都过(0,0)点和(1,1)
点;(2)在第一象限内,函数值 随x 的
增大而增大,即在(0,+∞)上
是增函 数。 (1)图象都过(1,1)点;
(2)在第一象限内,函数值随 x 的增大
而减小,即在(0,+∞)上是减函数。(3)在第一象限,图象向上与y 轴无
限接近,向右与 x 轴无限接近。
★当 为奇数时,幂函数为奇函数,
★当 为偶数时,幂函数为偶函数
如果函数 是幂函数,
且在区间(0,+∞)内是减函数,求满足条件的实数
m的集合。
解:依题意,得 解得 或当 时,函数为当 时,函数为所以例1、符合题意 不合题意,舍去1、求下列幂函数的定义域:解:设所求幂函数为因为函数过点 ,所以所以故所求的幂函数为练习3、 如图所示,曲线是幂函数 在第一象限内的图象,已知 a分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1的右侧,指
数大的在上,指数小的在下;在Y轴与直线x =1之间正好相反。
3、 如图所示,曲线是幂函数 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ C4C2C3C11证明幂函数 在[0,+∞)上是增函数.例2、证明一:所以幂函数 在[0,+∞)上是增函数.任取 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; (1)作差法:若给出的函数是有根号的式子,往往采用有 理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以幂函数定义五个特殊幂函数图象基本性质本节知识结构:
数函数2、如果a一定, b 随N的变化而变化,我们建立了
对数函数设想:如果b一定, N随a的变化而变化,是不是也应该可以确定了一个函数呢?函数的生活实例问题1:如果张红购买了每千克1元的蔬菜w千克,那么她
需要付的钱数 元,
问题2:如果正方形的边长为a,那么正方形的面积
是 ,
问题3:如果正方体的边长为a,那么正方体的体积是
问题4:如果一个正方形场地的面积为S,那么这个正方形的边长
,
问题5:如果某人t s内骑车行进了1km,那么他骑车的平均速度
V=t?1 km/s
PwSay=xy=x2y=x3y=x-1P=W____是____的函数____是____的函数V是a的函数a是S的函数V是t 的函数S=a2V=a3以上问题中的函数有什么共同特征?(1)都是函数;
(2)均是以自变量为底的幂;
(3)指数为常数;
(4)幂前的系数也为1。
上述问题中涉及的函数,都是形如
的函数幂函数的一般概念: 一般地,函数
幂函数的结构特征
你能说出幂函数与指数函数的区别吗?3. 幂前的系数也为11.自变量为底2.指数为常数叫做幂函数,其中x为自变量,a为常数。试判断下列函数是不是幂函数下面研究幂函数 研究图象的性质,一般包括:定义域、值域、单调性、奇偶性、过定点的情况等研究 。函数图象的画法是:列表描点连线奇偶
奇非奇
非偶奇RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,几个幂函数的性质在R上增在[0,+∞)
上增,在(-∞,0]上
减,在[0,+∞)上
增,在(0,+∞)
上减在第一象限内,函数图象的变化趋势与指数有什么关系?
y=x3a > 0a < 0
(1)图象都过(0,0)点和(1,1)
点;(2)在第一象限内,函数值 随x 的
增大而增大,即在(0,+∞)上
是增函 数。 (1)图象都过(1,1)点;
(2)在第一象限内,函数值随 x 的增大
而减小,即在(0,+∞)上是减函数。(3)在第一象限,图象向上与y 轴无
限接近,向右与 x 轴无限接近。
★当 为奇数时,幂函数为奇函数,
★当 为偶数时,幂函数为偶函数
如果函数 是幂函数,
且在区间(0,+∞)内是减函数,求满足条件的实数
m的集合。
解:依题意,得 解得 或当 时,函数为当 时,函数为所以例1、符合题意 不合题意,舍去1、求下列幂函数的定义域:解:设所求幂函数为因为函数过点 ,所以所以故所求的幂函数为练习3、 如图所示,曲线是幂函数 在第一象限内的图象,已知 a分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1的右侧,指
数大的在上,指数小的在下;在Y轴与直线x =1之间正好相反。
3、 如图所示,曲线是幂函数 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ C4C2C3C11证明幂函数 在[0,+∞)上是增函数.例2、证明一:所以幂函数 在[0,+∞)上是增函数.任取 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; (1)作差法:若给出的函数是有根号的式子,往往采用有 理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以幂函数定义五个特殊幂函数图象基本性质本节知识结构:
