苏教版六年级下册数学总复习 图形与几何 立体图形的认识(课件)(共27张ppt)
文档属性
| 名称 | 苏教版六年级下册数学总复习 图形与几何 立体图形的认识(课件)(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 20:48:16 | ||
图片预览



文档简介
(共27张PPT)
总复习
立体图形的认识
七
2.图形与几何
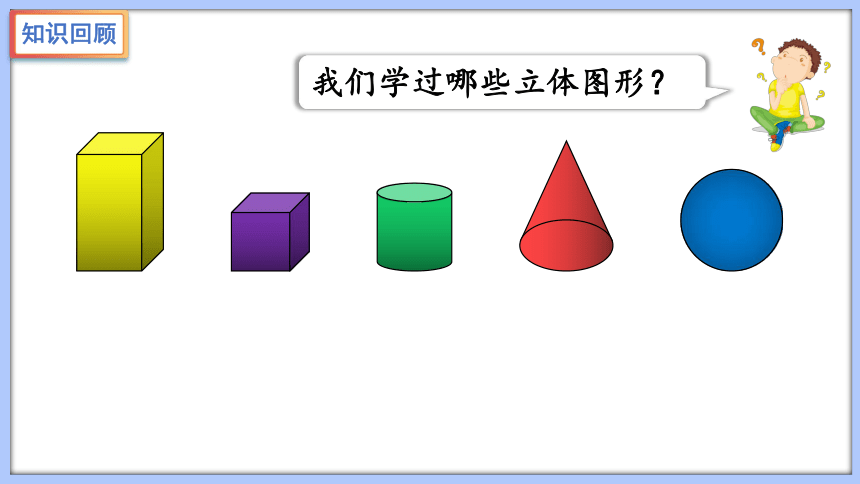
知识回顾
我们学过哪些立体图形?
说出下面每个立体图形的名称、特征以及图中字母的含义,再试着把它们分成两类。
(教材第92页)
正方体是特殊的长方体吗?为什么?
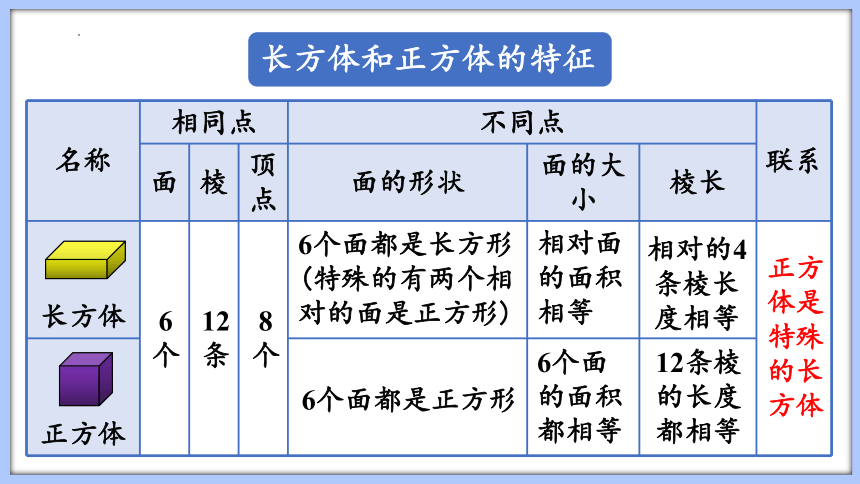
长方体和正方体的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长 长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
圆柱和圆锥的特征
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面圆心之间的距离叫作高,有无数条长度相等的高。
顶点到底面圆心的距离叫作高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
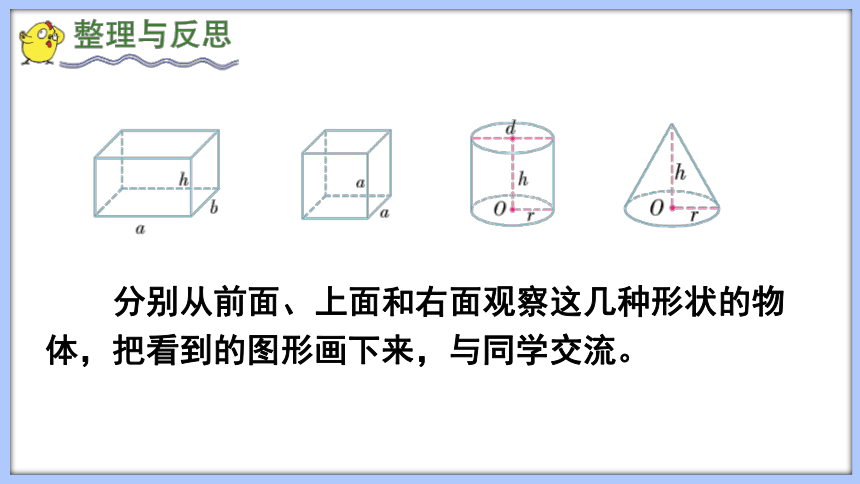
分别从前面、上面和右面观察这几种形状的物体,把看到的图形画下来,与同学交流。
a
b
h
a
b
h
前
后
左
右
上
下
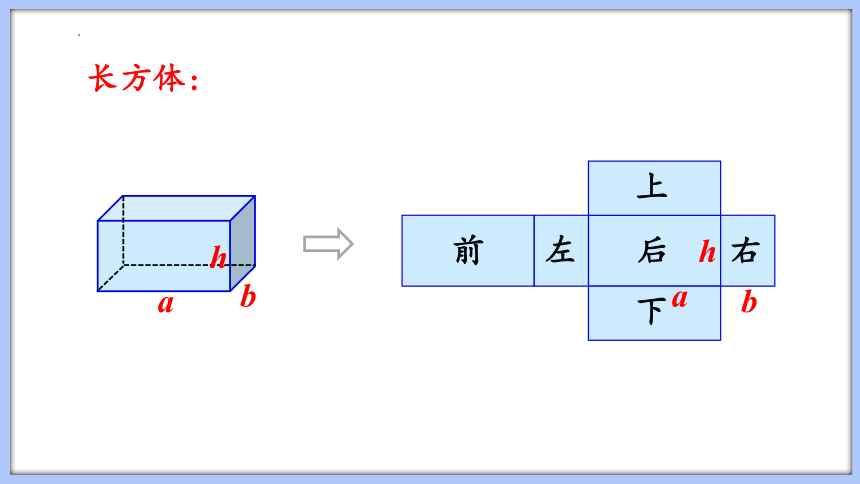
长方体:
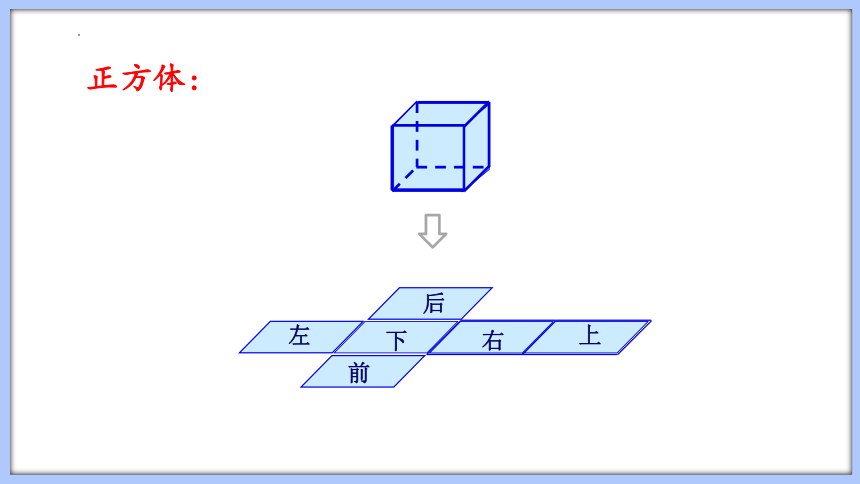
上
下
前
后
左
右
正方体:
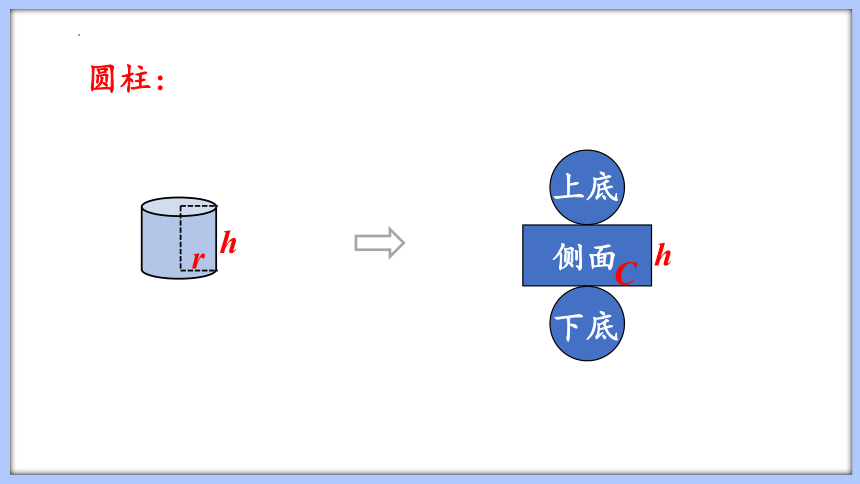
圆柱:
r
h
C
侧面
上底
下底
h
展开图
圆锥:
圆柱与圆锥可以各由什么平面图形旋转而成?
圆柱可以由一个长方形绕着它的一
条边旋转360°(或由矩形绕着它
的一条对称轴旋转180°)得到。
圆柱与圆锥可以各由什么平面图形旋转而成?
圆锥可以由一个直角三角形绕着它的一条直角边旋转360°得到。
1.下图是一个长方体展开图的前面、下面和左面。画出展开图的另外3个面。
(教材第92页)
2.从下面的长方形纸上剪下一部分,折成一个棱长
2厘米的正方体,可以怎样剪?设计两种不同的方案,在图中涂色表示。
3.用铁丝焊接一个长6厘米、宽5厘米、高4厘米的长方体框架,至少需要铁丝多少厘米?如果要焊接一个棱长5厘米的正方体框架呢?
(6+5+4)×4=60(厘米)
5×12=60(厘米)
答:至少需要铁丝60厘米,如果要焊接一个棱长5厘米的正方体框架至少也需要铁丝60厘米。
4.以下面的长方形或三角形的一条边为轴旋转一周,会形成怎样的立体图形?先想一想,再连一连。
5.从前面、右面和上面观察下面的物体,看到的各是什么形状?画一画。
√
6.李兵用同样大的正方体摆成了一个长方体。右图分别是他从前面和上面看到的图形。
从右面看到的是下面第几个图形?
①
②
③
④
7.用6个同样大的正方体摆成的物体,从前面看到的形状如右图。摆一摆,并分别从右面和上面看一看,各是什么形状?
7.用6个同样大的正方体摆成的物体,从前面看到的形状如右图。摆一摆,并分别从右面和上面看一看,各是什么形状?
从右面看
从上面看
√
下面4个正方体中,有一个是用右边的图形折成的。先猜一猜是哪个,再做一做。
根据展开图中彩带和桃心的位置关系进行思考。
正面
1.在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
左面
上面
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
巩固练习
2.小明用一根铁丝做成一个正方体框架。已知这个正方体框架的一个面的面积是49平方厘米,这根铁丝至少长( )厘米。
84
正方体的每个面都是正方形,因为49=72,所以正方体的棱长为7厘米,铁丝的长度也就是12条棱的长度和,即12×7=84(厘米)。
下面这些图分别是从哪个方向看到的?
3.
左面
上面
正面
1.按从不同方向看到的图形摆出几何体。
搭几何体时,先从一个方向确定基本形状,然后从另外两面确定层数和每层的个数。
(1)
左面
上面
正面
拓展提升
(2)
左面
上面
正面
1.按从不同方向看到的图形摆出几何体。
2.把下面这个展开图折成一个长方体(字母在长方体的
内侧)。
A
B C D
E F
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么哪一面在上面?
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度?
F面
E面或C面
至少要量出A、B、C、D、E、F面中任意3个不同的边长。
总复习
立体图形的认识
七
2.图形与几何
知识回顾
我们学过哪些立体图形?
说出下面每个立体图形的名称、特征以及图中字母的含义,再试着把它们分成两类。
(教材第92页)
正方体是特殊的长方体吗?为什么?
长方体和正方体的特征
名称 相同点 不同点 联系
面 棱 顶点 面的形状 面的大小 棱长 长方体
正方体
6个
12条
8个
6个面都是长方形(特殊的有两个相对的面是正方形)
6个面都是正方形
相对面的面积相等
6个面的面积都相等
相对的4条棱长度相等
12条棱的长度都相等
正方体是特殊的长方体
圆柱和圆锥的特征
名称 特征
圆柱
圆锥
有3个面:上、下底面是相等的两个圆,侧面是曲面。
有2个面:底面是圆,侧面是曲面。
两个底面圆心之间的距离叫作高,有无数条长度相等的高。
顶点到底面圆心的距离叫作高,只有一条高。
侧面沿高剪开,展开后是长方形(正方形)。
侧面展开后可以得到一个扇形。
由长方形(正方形)的一边为轴旋转一周可以形成。
由直角三角形的一条直角边为轴旋转一周可以形成。
分别从前面、上面和右面观察这几种形状的物体,把看到的图形画下来,与同学交流。
a
b
h
a
b
h
前
后
左
右
上
下
长方体:
上
下
前
后
左
右
正方体:
圆柱:
r
h
C
侧面
上底
下底
h
展开图
圆锥:
圆柱与圆锥可以各由什么平面图形旋转而成?
圆柱可以由一个长方形绕着它的一
条边旋转360°(或由矩形绕着它
的一条对称轴旋转180°)得到。
圆柱与圆锥可以各由什么平面图形旋转而成?
圆锥可以由一个直角三角形绕着它的一条直角边旋转360°得到。
1.下图是一个长方体展开图的前面、下面和左面。画出展开图的另外3个面。
(教材第92页)
2.从下面的长方形纸上剪下一部分,折成一个棱长
2厘米的正方体,可以怎样剪?设计两种不同的方案,在图中涂色表示。
3.用铁丝焊接一个长6厘米、宽5厘米、高4厘米的长方体框架,至少需要铁丝多少厘米?如果要焊接一个棱长5厘米的正方体框架呢?
(6+5+4)×4=60(厘米)
5×12=60(厘米)
答:至少需要铁丝60厘米,如果要焊接一个棱长5厘米的正方体框架至少也需要铁丝60厘米。
4.以下面的长方形或三角形的一条边为轴旋转一周,会形成怎样的立体图形?先想一想,再连一连。
5.从前面、右面和上面观察下面的物体,看到的各是什么形状?画一画。
√
6.李兵用同样大的正方体摆成了一个长方体。右图分别是他从前面和上面看到的图形。
从右面看到的是下面第几个图形?
①
②
③
④
7.用6个同样大的正方体摆成的物体,从前面看到的形状如右图。摆一摆,并分别从右面和上面看一看,各是什么形状?
7.用6个同样大的正方体摆成的物体,从前面看到的形状如右图。摆一摆,并分别从右面和上面看一看,各是什么形状?
从右面看
从上面看
√
下面4个正方体中,有一个是用右边的图形折成的。先猜一猜是哪个,再做一做。
根据展开图中彩带和桃心的位置关系进行思考。
正面
1.在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
左面
上面
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
巩固练习
2.小明用一根铁丝做成一个正方体框架。已知这个正方体框架的一个面的面积是49平方厘米,这根铁丝至少长( )厘米。
84
正方体的每个面都是正方形,因为49=72,所以正方体的棱长为7厘米,铁丝的长度也就是12条棱的长度和,即12×7=84(厘米)。
下面这些图分别是从哪个方向看到的?
3.
左面
上面
正面
1.按从不同方向看到的图形摆出几何体。
搭几何体时,先从一个方向确定基本形状,然后从另外两面确定层数和每层的个数。
(1)
左面
上面
正面
拓展提升
(2)
左面
上面
正面
1.按从不同方向看到的图形摆出几何体。
2.把下面这个展开图折成一个长方体(字母在长方体的
内侧)。
A
B C D
E F
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么哪一面在上面?
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度?
F面
E面或C面
至少要量出A、B、C、D、E、F面中任意3个不同的边长。
