苏教版六年级下册数学总复习 图形与几何 立体图形的表面积和体积(2)(课件)(共30张PPT)
文档属性
| 名称 | 苏教版六年级下册数学总复习 图形与几何 立体图形的表面积和体积(2)(课件)(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 21:09:49 | ||
图片预览









文档简介
(共30张PPT)
总复习
立体图形的表面积和体积(2)
七
2.图形与几何
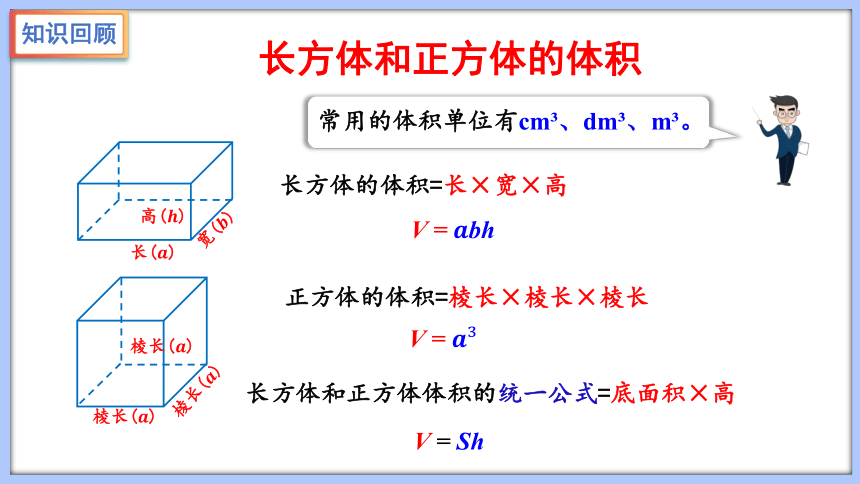
长()
宽()
高()
长方体的体积=长×宽×高
V =bh
棱长()
棱长()
棱长()
正方体的体积=棱长×棱长×棱长
V =
长方体和正方体体积的统一公式=底面积×高
V = Sh
常用的体积单位有cm 、dm 、m 。
长方体和正方体的体积
知识回顾
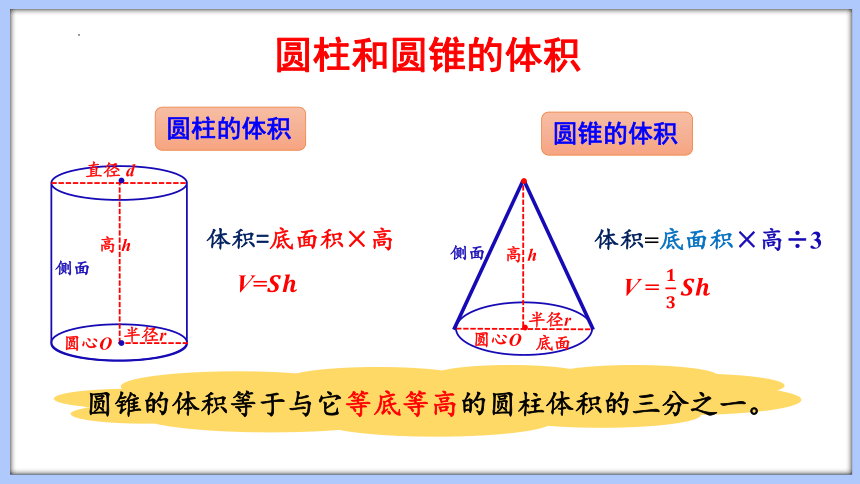
圆柱和圆锥的体积
圆柱的体积
体积=底面积×高
V=
圆心O
.
半径r
高 h
直径 d
侧面
.
体积=底面积×高÷3
V =
.
半径r
高 h
侧面
底面
圆心O
.
圆锥的体积
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
长方体、正方体、圆柱的体积:V=S底h
求物体的体积是从物体的外部来测量相关数据的,求物体的容积是从物体的内部来测量相关数据的。
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
求不规则物体体积的方法:
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
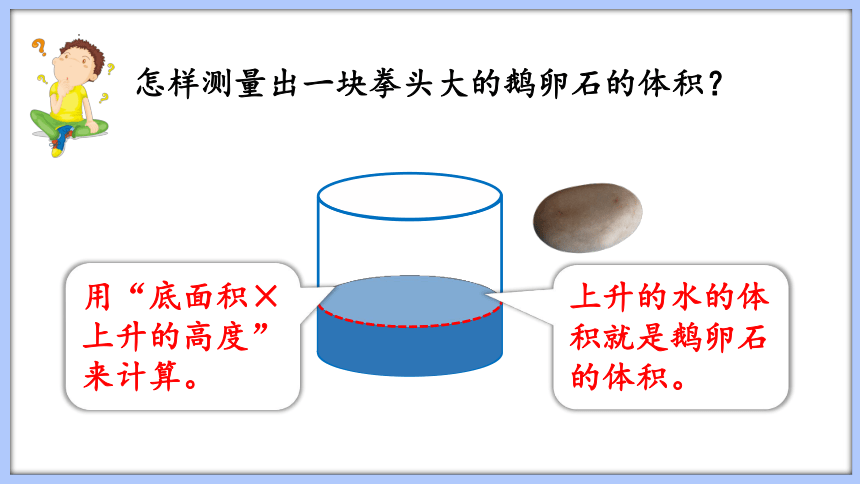
上升的水的体积就是鹅卵石的体积。
用“底面积×上升的高度”来计算。
怎样测量出一块拳头大的鹅卵石的体积?
9.学校有一个圆形储水箱,它的侧面由一块边长6.28分米的正方形铁皮围成。这个储水箱最多能储水多少升?(接缝处所用材料略去不计)
6.28÷3.14÷2=1(分米)
3.14×12×6.28=19.7192(立方分米)
19.7192立方分米=19.7192升
答:这个储水箱最多能储水19.7192升。
(教材第95页)
10.一个圆锥形小麦堆,底面周长是12.56米,高1.5米。如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
12.56÷3.14÷2=2(米)
3.14×22×1.5× =6.28(立方米)
750×6.28=4710(千克)
4710千克=4.71吨
答:这堆小麦大约重4.71吨。
11.一种计算机包装箱标注的尺寸是380×260×530(单位:mm )。它的体积是多少立方分米?做这个包装箱至少需要硬纸板多少平方分米?(用计算器计算,得数保留两位小数)
380毫米=3.8分米
260毫米=2.6分米
530毫米=5.3分米
3.8×2.6×5.3≈52.36(立方分米)
答:它的体积约是52.36平方分米。
11.一种计算机包装箱标注的尺寸是380×260×530(单位:mm )。它的体积是多少立方分米?做这个包装箱至少需要硬纸板多少平方分米?(用计算器计算,得数保留两位小数)
(3.8×2.6+3.8×5.3+2.6×5.3)×2
=(9.88+20.14+13.78)×2
=43.8×2
=87.60(平方分米)
答:做这个包装箱至少需要硬纸板87.60平方分米。
12.一个圆柱形水池,底面直径是20米,深2米。
(1)水池的占地面积是多少平方米?
3.14×(20÷2)2=314(平方米)
答:水池的占地面积是314平方米。
(2)在水池的侧面和底面抹上水泥,抹水泥部分的面积是多少平方米?
3.14×20×2=125.6(平方米)
314+125.6=439.6(平方米)
答:抹水泥部分的面积是439.6平方米。
12.一个圆柱形水池,底面直径是20米,深2米。
(3)池内最多能蓄水多少吨?(每立方米水重1吨)
314×2=628(立方米)
628×1=628(吨)
答:池内最多能盛水628吨。
仓库里有以下四种规格的长方形、正方形铁皮。
①长0.6米,宽0.4米; ②长0.6米,宽0.5米;
③长0.5米,宽0.4米; ④边长0.4米。
张师傅想从中选5张铁皮,焊接成一个无盖的长方体(或正方体)水箱,可以选哪几种规格的铁皮,各要选几张?你能找到多少种不同的选法?在下表中填一填。
2
2
1
0
0.12
0
0
4
1
0.08
4
0
0
1
0.096
0
0
0
5
0.064
(选法不唯一)
1.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
巩固练习
2.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
3.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
12÷3=4(cm)
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
4.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,如果把它捏成同样高的一个圆柱,那么该圆柱的底面积是多少平方厘米?
圆锥体积=底面积×高×-
13
12×6×-=24(立方厘米)
13
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
答:该圆柱的底面积是4平方厘米。
圆锥变成圆柱的过程中,体积不变。
圆柱的底面直径
=圆柱的高
=正方体的棱长
=20 cm
5.一个箱子下半部的形状是棱长为 20 cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
20 cm
20 cm
20 cm
箱子的表面积=圆柱表面积的一半+正方体5个面的面积。
圆柱的表面积:
3.14×(20÷2)2×2+3.14×20×20
=628+1256
=1884(cm2)
箱子的表面积:
1884÷2+20×20×5
=942+2000
=2942(cm2)
20 cm
20 cm
20 cm
5.一个箱子下半部的形状是棱长为 20 cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
圆柱的体积:
3.14×(20÷2)2×20=6280(cm3)
箱子的体积:
6280÷2+203=11140(cm3)
答:它的表面积是2942 cm2,体积是11140 cm3。
20 cm
20 cm
20 cm
5.一个箱子下半部的形状是棱长为 20 cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
箱子的体积=圆柱体积的一半+正方体的体积
6.下图是由棱长为5 cm的正方体搭成的几何体,所有表面都涂成了绿色。
(1)其中一共有多少个正方体?这个几何体的体积是多少?
5×5×5×10=1250(cm3)
答:其中一共有10个正方体,这个几何体的体积是1250 cm3。
用学具摆一摆、看一看、想一想、数一数。
(2)只有2个面涂色的正方体有多少个?
答:只有2个面涂色的正方体有2个,
2
2
3
4
4
4
4
3
4
4
只有3个面涂色的正方体有2个,
只有4个面涂色的正方体有6个。
(3)只有3个面涂色的正方体有多少个?
(4)只有4个面涂色的正方体有多少个?
6.下图是由棱长为5 cm的正方体搭成的几何体,所有表面都涂成了绿色。
用学具摆一摆、看一看、想一想、数一数。
15*.一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10 cm2,涂色部分的面积是多少?
涂色部分的面积=圆的面积÷4
答:涂色部分的面积是7.85 cm2。
3.14×10÷4=7.85(cm2)
圆的面积=圆周率×
半径的平方
边长的平方
正方形的面积
16*.用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
由题意可知,铁丝的长度就是长方体(或正方体)的棱长总和。长方体有4组长、宽、高,24÷4=
6(cm),可以得出一组长、宽、高的和是6 cm。
求怎样围框架用纸最多,就是要使长方体(或正方体)的表面积最大。
形状 长/cm 宽/cm 高/cm 表面积/cm2
1
1
4
(1×4)×4+(1×1)×2=18
1
2
3
(1×2+1×3+2×3)×2=22
2
2
2
2×2×6=24
长方体
正方体
16*.用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
答:围成棱长为2 cm的正方体框架用纸最多。
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,怎样旋转得到的圆锥的体积最大?
7 cm
9 cm
13
3.14×92×7×-=593.46(cm3)
拓展提升
以7厘米的直角边所在的直线为轴旋转,得到的圆锥的底面半径是9厘米,高是7厘米。
7 cm
9 cm
13
3.14×72×9×-=461.58(cm3)
593.46>461.58
答:以7厘米的直角边所在的直线为轴旋转,得到的圆锥的体积最大。
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,怎样旋转得到的圆锥的体积最大?
以9厘米的直角边所在的直线为轴旋转,得到的圆锥的底面半径是7厘米,高是9厘米。
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
正放或倒放时,酸奶和空的部分的体积和都是2.5 L;酸奶的体积不变,则两次空的部分体积也相等;正放时酸奶的体积加上倒放时空的部分的体积,和还是2.5 L。
20 cm
5
cm
2.5 L
20 cm
5
cm
2.5 L
2.5 L
2500÷(20+5)×20=2000(cm3)
答:瓶内酸奶的体积是2 L。
2.5 L=2500 cm3
2000 cm3=2 L
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
20 cm
5
cm
2.5 L
2.5 L
20 cm
5
cm
2.5 L
总复习
立体图形的表面积和体积(2)
七
2.图形与几何
长()
宽()
高()
长方体的体积=长×宽×高
V =bh
棱长()
棱长()
棱长()
正方体的体积=棱长×棱长×棱长
V =
长方体和正方体体积的统一公式=底面积×高
V = Sh
常用的体积单位有cm 、dm 、m 。
长方体和正方体的体积
知识回顾
圆柱和圆锥的体积
圆柱的体积
体积=底面积×高
V=
圆心O
.
半径r
高 h
直径 d
侧面
.
体积=底面积×高÷3
V =
.
半径r
高 h
侧面
底面
圆心O
.
圆锥的体积
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
长方体、正方体、圆柱的体积:V=S底h
求物体的体积是从物体的外部来测量相关数据的,求物体的容积是从物体的内部来测量相关数据的。
在容器中装满水,把不规则物体完全浸入水中,溢出水的体积就是不规则物体的体积。
求不规则物体体积的方法:
在粗细均匀的容器中倒入一定量的水,把不规则物体完全浸入水中,上升的水的体积就是不规则物体的体积。
利用体积不变的特征,把不规则物体转化成规则物体再进行计算。
溢出法
升高法
转化法
上升的水的体积就是鹅卵石的体积。
用“底面积×上升的高度”来计算。
怎样测量出一块拳头大的鹅卵石的体积?
9.学校有一个圆形储水箱,它的侧面由一块边长6.28分米的正方形铁皮围成。这个储水箱最多能储水多少升?(接缝处所用材料略去不计)
6.28÷3.14÷2=1(分米)
3.14×12×6.28=19.7192(立方分米)
19.7192立方分米=19.7192升
答:这个储水箱最多能储水19.7192升。
(教材第95页)
10.一个圆锥形小麦堆,底面周长是12.56米,高1.5米。如果每立方米小麦大约重750千克,这堆小麦大约重多少吨?
12.56÷3.14÷2=2(米)
3.14×22×1.5× =6.28(立方米)
750×6.28=4710(千克)
4710千克=4.71吨
答:这堆小麦大约重4.71吨。
11.一种计算机包装箱标注的尺寸是380×260×530(单位:mm )。它的体积是多少立方分米?做这个包装箱至少需要硬纸板多少平方分米?(用计算器计算,得数保留两位小数)
380毫米=3.8分米
260毫米=2.6分米
530毫米=5.3分米
3.8×2.6×5.3≈52.36(立方分米)
答:它的体积约是52.36平方分米。
11.一种计算机包装箱标注的尺寸是380×260×530(单位:mm )。它的体积是多少立方分米?做这个包装箱至少需要硬纸板多少平方分米?(用计算器计算,得数保留两位小数)
(3.8×2.6+3.8×5.3+2.6×5.3)×2
=(9.88+20.14+13.78)×2
=43.8×2
=87.60(平方分米)
答:做这个包装箱至少需要硬纸板87.60平方分米。
12.一个圆柱形水池,底面直径是20米,深2米。
(1)水池的占地面积是多少平方米?
3.14×(20÷2)2=314(平方米)
答:水池的占地面积是314平方米。
(2)在水池的侧面和底面抹上水泥,抹水泥部分的面积是多少平方米?
3.14×20×2=125.6(平方米)
314+125.6=439.6(平方米)
答:抹水泥部分的面积是439.6平方米。
12.一个圆柱形水池,底面直径是20米,深2米。
(3)池内最多能蓄水多少吨?(每立方米水重1吨)
314×2=628(立方米)
628×1=628(吨)
答:池内最多能盛水628吨。
仓库里有以下四种规格的长方形、正方形铁皮。
①长0.6米,宽0.4米; ②长0.6米,宽0.5米;
③长0.5米,宽0.4米; ④边长0.4米。
张师傅想从中选5张铁皮,焊接成一个无盖的长方体(或正方体)水箱,可以选哪几种规格的铁皮,各要选几张?你能找到多少种不同的选法?在下表中填一填。
2
2
1
0
0.12
0
0
4
1
0.08
4
0
0
1
0.096
0
0
0
5
0.064
(选法不唯一)
1.一个棱长是10 cm的正方体,是由两个同样大小的长方体拼成的,原来一个长方体的表面积是( )cm2,体积是( )cm3。
10 cm
10 cm
10 cm
5 cm
10÷2=5(cm)
长方体的长:
表面积:
5×10×4+10×10×2
=200+200
=400(cm2)
体积:
5×10×10=500(cm3)
400
500
巩固练习
2.一个长方体的表面积是184 cm2,底面积是20 cm2,底面周长是18 cm,这个长方体的体积是( )cm3。
160
20 cm2
20 cm2
184-20×2=144(cm2)
144 cm2
cm
侧面积=表面积-底面积×2
144÷18=8(cm)
高=侧面积÷底面周长
20×8=160(cm3)
体积=底面积×高
18 cm
3.如下图,一个圆锥的高是3 cm,沿着它的高平均切成两部分,表面积就增加12 cm2,原来圆锥的底面直径是( )cm。
4
12÷3=4(cm)
增加的部分是两个相同的三角形,增加部分的面积=底面直径×高。
4.一块圆锥形橡皮泥,底面积是12平方厘米,高是6厘米,如果把它捏成同样高的一个圆柱,那么该圆柱的底面积是多少平方厘米?
圆锥体积=底面积×高×-
13
12×6×-=24(立方厘米)
13
圆柱的底面积=体积÷高
24÷6=4(平方厘米)
答:该圆柱的底面积是4平方厘米。
圆锥变成圆柱的过程中,体积不变。
圆柱的底面直径
=圆柱的高
=正方体的棱长
=20 cm
5.一个箱子下半部的形状是棱长为 20 cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
20 cm
20 cm
20 cm
箱子的表面积=圆柱表面积的一半+正方体5个面的面积。
圆柱的表面积:
3.14×(20÷2)2×2+3.14×20×20
=628+1256
=1884(cm2)
箱子的表面积:
1884÷2+20×20×5
=942+2000
=2942(cm2)
20 cm
20 cm
20 cm
5.一个箱子下半部的形状是棱长为 20 cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
圆柱的体积:
3.14×(20÷2)2×20=6280(cm3)
箱子的体积:
6280÷2+203=11140(cm3)
答:它的表面积是2942 cm2,体积是11140 cm3。
20 cm
20 cm
20 cm
5.一个箱子下半部的形状是棱长为 20 cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
箱子的体积=圆柱体积的一半+正方体的体积
6.下图是由棱长为5 cm的正方体搭成的几何体,所有表面都涂成了绿色。
(1)其中一共有多少个正方体?这个几何体的体积是多少?
5×5×5×10=1250(cm3)
答:其中一共有10个正方体,这个几何体的体积是1250 cm3。
用学具摆一摆、看一看、想一想、数一数。
(2)只有2个面涂色的正方体有多少个?
答:只有2个面涂色的正方体有2个,
2
2
3
4
4
4
4
3
4
4
只有3个面涂色的正方体有2个,
只有4个面涂色的正方体有6个。
(3)只有3个面涂色的正方体有多少个?
(4)只有4个面涂色的正方体有多少个?
6.下图是由棱长为5 cm的正方体搭成的几何体,所有表面都涂成了绿色。
用学具摆一摆、看一看、想一想、数一数。
15*.一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10 cm2,涂色部分的面积是多少?
涂色部分的面积=圆的面积÷4
答:涂色部分的面积是7.85 cm2。
3.14×10÷4=7.85(cm2)
圆的面积=圆周率×
半径的平方
边长的平方
正方形的面积
16*.用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
由题意可知,铁丝的长度就是长方体(或正方体)的棱长总和。长方体有4组长、宽、高,24÷4=
6(cm),可以得出一组长、宽、高的和是6 cm。
求怎样围框架用纸最多,就是要使长方体(或正方体)的表面积最大。
形状 长/cm 宽/cm 高/cm 表面积/cm2
1
1
4
(1×4)×4+(1×1)×2=18
1
2
3
(1×2+1×3+2×3)×2=22
2
2
2
2×2×6=24
长方体
正方体
16*.用一根长24 cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
答:围成棱长为2 cm的正方体框架用纸最多。
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,怎样旋转得到的圆锥的体积最大?
7 cm
9 cm
13
3.14×92×7×-=593.46(cm3)
拓展提升
以7厘米的直角边所在的直线为轴旋转,得到的圆锥的底面半径是9厘米,高是7厘米。
7 cm
9 cm
13
3.14×72×9×-=461.58(cm3)
593.46>461.58
答:以7厘米的直角边所在的直线为轴旋转,得到的圆锥的体积最大。
1.将一个直角边分别为7厘米、9厘米的直角三角形,以一条直角边所在的直线为轴旋转,怎样旋转得到的圆锥的体积最大?
以9厘米的直角边所在的直线为轴旋转,得到的圆锥的底面半径是7厘米,高是9厘米。
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
正放或倒放时,酸奶和空的部分的体积和都是2.5 L;酸奶的体积不变,则两次空的部分体积也相等;正放时酸奶的体积加上倒放时空的部分的体积,和还是2.5 L。
20 cm
5
cm
2.5 L
20 cm
5
cm
2.5 L
2.5 L
2500÷(20+5)×20=2000(cm3)
答:瓶内酸奶的体积是2 L。
2.5 L=2500 cm3
2000 cm3=2 L
2.一个容积为2.5 L的酸奶瓶,瓶内酸奶高为20 cm。把酸奶瓶盖拧紧倒放,这时瓶中空的部分高为5 cm,请你算一算,瓶内酸奶的体积是多少?
20 cm
5
cm
2.5 L
2.5 L
20 cm
5
cm
2.5 L
