4-1 数列的概念(第二课时) 课件(共24张PPT)
文档属性
| 名称 | 4-1 数列的概念(第二课时) 课件(共24张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 644.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:21:15 | ||
图片预览







文档简介
(共24张PPT)
4.1 数列的概念
(第二课时)
2.数列的分类:
(1)按项数多少分类:
有穷数列 ,无穷数列。
(2)按增减性分类:
递增数列、递减数列、常数列。
温故知新
1.数列的有关概念
3.数列与函数
数列是一种特殊的函数,数列的项是序号的函数。
4.数列通项公式
提升训练:
例3.如果数列{an}的通项公式为an=n2+2n,那么120是不是这个数列的项,如果是,是第几项?
解:令n2+2n=120 ,
解得 n=-12(舍)或n=10,
所以 120是数列的项,是第10项。
新知探究
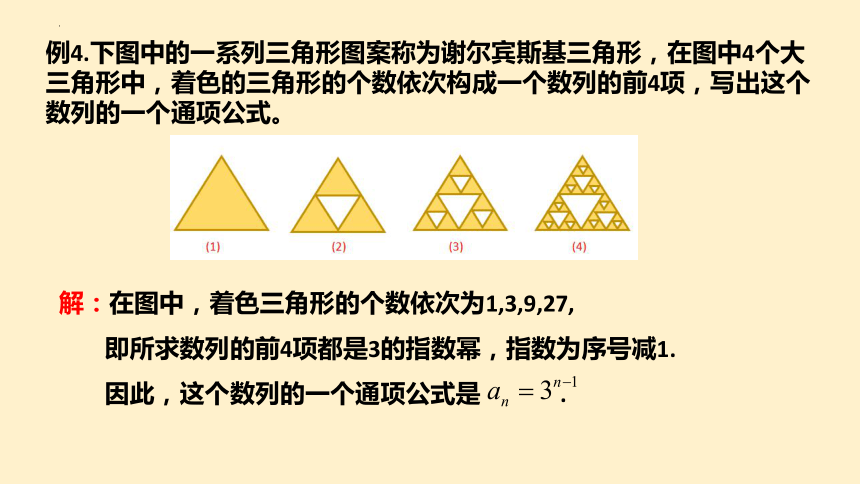
例4.下图中的一系列三角形图案称为谢尔宾斯基三角形,在图中4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的一个通项公式。
解:在图中,着色三角形的个数依次为1,3,9,27,
即所求数列的前4项都是3的指数幂,指数为序号减1.
因此,这个数列的一个通项公式是 .
换个角度观察图中的4个图形,可以发现,
①a1=1,
②每个图形中的着色三角形都在下一个图形中分裂为3个着色小三角形和1个无色小三角形,
③从第2个图形开始,每个图形中着色三角形的个数都是前一个图形中着色三角形个数的3倍。
这样,例4中的数列的前4项满足 a1=1, a2 =3 a1, a3 =3a2, a4 =3a3,由此猜测这个数列满足公式
递推公式:
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
已知数列的第1项(或前几项)以及递推公式,就能求出数列的每一项。
递推公式:
例5:已知数列的第1项是1,以后的各项由公式 给出,写出这个数列的前5项。
通项公式和的递推公式之间的差别与联系:
练习1 根据递推公式,分别写出它的前 5 项,并归纳出通项公式:
(2)a1=1,an+1=
2an
an+2
(n∈N*).
解:(1)a1=0,a2=a1+1=1,a3=a2+3=4,
a4=a3+5=9,a5=a4+7=16.
由a1=02,a2=12,a3=22,a4=32,a5=42,可归纳出an=(n-1)2.
(1)a1=0,an+1=an+(2n-1)(n∈N*);
在数列{an}中,
(1)求数列{an}的前5项
(2)求a2021
解:(1) ,a2=-1,a3=2, ,a5=-1
(2)周期为3,2021=3×673+2,所以a2021=a3×673+2=a2=-1。
练习2
我们把数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn ,即
Sn =a1+a2+...+an.
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
练习:
(1)数列{an}的通项公式为an=n ,则S3= ,S5= ,S1= 。
(2)数列{an}的前n项和为Sn,S7=30,S8=40,则a8= 。
思考:an与Sn的关系?
6
15
10
数列的前n公式:
1
我们把数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn ,即
Sn =a1+a2+...+an.
显然S1=a1 ,而Sn-1=a1+a2+…+an-1(n≥2) ,于是我们有
an与Sn的关系
例5.已知数列{an}的前几项和公式为Sn =n2+n,
(1)求S3,S5,Sn-1;(2)求出{an}的通项公式.
解:(1)S3=32+3=12,S5=52+5=30, Sn-1=(n-1)2+(n-1)=n2-n.
(2)当n=1时,a1=S1=2,
当n>1时,an=Sn-Sn-1= n2+n -[(n-1) +(n-1)]=2n(n≥2),①
将n=1代入①式得,2×1=2=a1
所以当n=1时,①式依然成立.
故{an}的通项公式是an=2n.
1.已知数列{an}的前几项和公式为Sn =-2n2,求{an}的通项公式。
2.已知数列{an}的前几项和公式为Sn =n2+4 ,求{an}的通项公式。
解:(1)当n=1时,a1=S1=-2,
当n>1时,an=Sn-Sn-1= -2n2 -[-2(n-1) ]=2-4n(n≥2),①
将n=1代入①式得,2-4=-2=a1
所以当n=1时,①式依然成立.
故{an}的通项公式是an=2-4n.
巩固练习
解:(2)当n=1时,a1=S1=1+5=6;
当n≥2时, an=Sn-Sn-1=(n2+5)-[(n-1)2+5]=2n-1.①
将n=1代入①式得,2-1=1≠6=a1
所以当n=1时,①式不成立.
1.已知数列{an}的前几项和公式为Sn =-2n2,求{an}的通项公式
2.已知数列{an}的前几项和公式为Sn =n2+5 ,求{an}的通项公式
巩固练习
1.递推公式:(1)初始值;2)递推关系式
已知数列的递推公式,求前几项并猜出通项公式。
课堂小结
课外探究
4.1 数列的概念
(第二课时)
2.数列的分类:
(1)按项数多少分类:
有穷数列 ,无穷数列。
(2)按增减性分类:
递增数列、递减数列、常数列。
温故知新
1.数列的有关概念
3.数列与函数
数列是一种特殊的函数,数列的项是序号的函数。
4.数列通项公式
提升训练:
例3.如果数列{an}的通项公式为an=n2+2n,那么120是不是这个数列的项,如果是,是第几项?
解:令n2+2n=120 ,
解得 n=-12(舍)或n=10,
所以 120是数列的项,是第10项。
新知探究
例4.下图中的一系列三角形图案称为谢尔宾斯基三角形,在图中4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的一个通项公式。
解:在图中,着色三角形的个数依次为1,3,9,27,
即所求数列的前4项都是3的指数幂,指数为序号减1.
因此,这个数列的一个通项公式是 .
换个角度观察图中的4个图形,可以发现,
①a1=1,
②每个图形中的着色三角形都在下一个图形中分裂为3个着色小三角形和1个无色小三角形,
③从第2个图形开始,每个图形中着色三角形的个数都是前一个图形中着色三角形个数的3倍。
这样,例4中的数列的前4项满足 a1=1, a2 =3 a1, a3 =3a2, a4 =3a3,由此猜测这个数列满足公式
递推公式:
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
已知数列的第1项(或前几项)以及递推公式,就能求出数列的每一项。
递推公式:
例5:已知数列的第1项是1,以后的各项由公式 给出,写出这个数列的前5项。
通项公式和的递推公式之间的差别与联系:
练习1 根据递推公式,分别写出它的前 5 项,并归纳出通项公式:
(2)a1=1,an+1=
2an
an+2
(n∈N*).
解:(1)a1=0,a2=a1+1=1,a3=a2+3=4,
a4=a3+5=9,a5=a4+7=16.
由a1=02,a2=12,a3=22,a4=32,a5=42,可归纳出an=(n-1)2.
(1)a1=0,an+1=an+(2n-1)(n∈N*);
在数列{an}中,
(1)求数列{an}的前5项
(2)求a2021
解:(1) ,a2=-1,a3=2, ,a5=-1
(2)周期为3,2021=3×673+2,所以a2021=a3×673+2=a2=-1。
练习2
我们把数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn ,即
Sn =a1+a2+...+an.
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
练习:
(1)数列{an}的通项公式为an=n ,则S3= ,S5= ,S1= 。
(2)数列{an}的前n项和为Sn,S7=30,S8=40,则a8= 。
思考:an与Sn的关系?
6
15
10
数列的前n公式:
1
我们把数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn ,即
Sn =a1+a2+...+an.
显然S1=a1 ,而Sn-1=a1+a2+…+an-1(n≥2) ,于是我们有
an与Sn的关系
例5.已知数列{an}的前几项和公式为Sn =n2+n,
(1)求S3,S5,Sn-1;(2)求出{an}的通项公式.
解:(1)S3=32+3=12,S5=52+5=30, Sn-1=(n-1)2+(n-1)=n2-n.
(2)当n=1时,a1=S1=2,
当n>1时,an=Sn-Sn-1= n2+n -[(n-1) +(n-1)]=2n(n≥2),①
将n=1代入①式得,2×1=2=a1
所以当n=1时,①式依然成立.
故{an}的通项公式是an=2n.
1.已知数列{an}的前几项和公式为Sn =-2n2,求{an}的通项公式。
2.已知数列{an}的前几项和公式为Sn =n2+4 ,求{an}的通项公式。
解:(1)当n=1时,a1=S1=-2,
当n>1时,an=Sn-Sn-1= -2n2 -[-2(n-1) ]=2-4n(n≥2),①
将n=1代入①式得,2-4=-2=a1
所以当n=1时,①式依然成立.
故{an}的通项公式是an=2-4n.
巩固练习
解:(2)当n=1时,a1=S1=1+5=6;
当n≥2时, an=Sn-Sn-1=(n2+5)-[(n-1)2+5]=2n-1.①
将n=1代入①式得,2-1=1≠6=a1
所以当n=1时,①式不成立.
1.已知数列{an}的前几项和公式为Sn =-2n2,求{an}的通项公式
2.已知数列{an}的前几项和公式为Sn =n2+5 ,求{an}的通项公式
巩固练习
1.递推公式:(1)初始值;2)递推关系式
已知数列的递推公式,求前几项并猜出通项公式。
课堂小结
课外探究
