4-2-1 等差数列的概念(第二课时) 课件(共19张PPT)
文档属性
| 名称 | 4-2-1 等差数列的概念(第二课时) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 887.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览


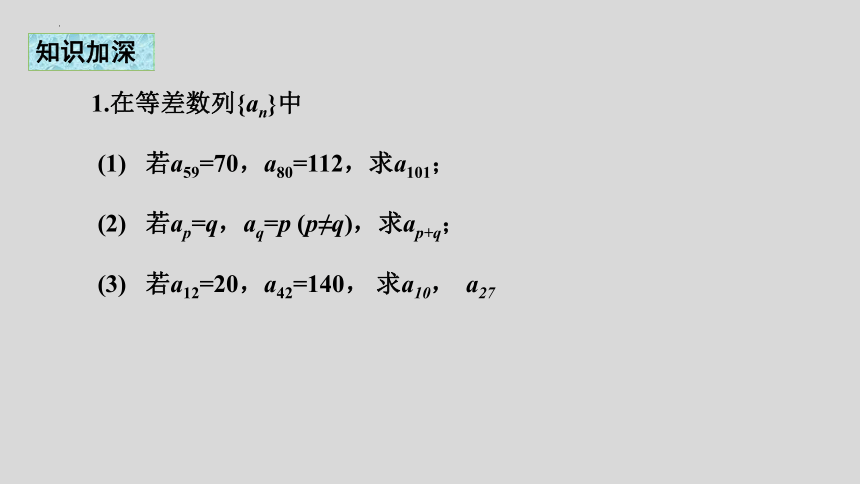




文档简介
(共19张PPT)
4.2.1等差数列的概念
(第二课时)
1.等差数列的定义:
4.等差数列的函数特征:
3.等差数列的通项公式:
2.等差中项的定义:
函数图象上所有的点在同一条直线上:
d>0,等差数列单调增;d<0,等差数列单调减;
d=0,等差数列为常函数.
如果在 与 中间插入一个数A,使 ,A, 成等差数列,那么A叫做 与 的等差中项.
an=am+(n-m)d
累加法
an=a1+(n-1)d=dn+(a1-d),
f(x)=dx+(a1-d)
复习回顾
5.等差数列的判定方法:
定义法
知识加深
1.在等差数列{an}中
(1) 若a59=70,a80=112,求a101;
(2) 若ap=q,aq=p (p≠q),求ap+q;
(3) 若a12=20,a42=140, 求a10, a27
例1.
解:
知识应用
典例分析
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:a1,a2,a3,a4,a5,...
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
典例分析
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
解:(1)设数列{bn}的公差为d′.
由题意可知,b1=a1,b5=a2,于是b5-b1=a2-a1=8.
∵b5-b1=4d′,所以4d′ =8,所以d′ =2.
∴bn=2+(n-1)×2=2n
∴数列{bn}的通项公式是bn=2n.
典例分析
分析:(2)①先求b29=?
②再求an
③令an= ,解出n
解法1:(2)由(1)可得b29=2×29=58
因为a1=2,d=8 所以an=8n-6
令8n-6=58 解得n=8
所以b29是数列{an}项,是第8项。
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
典例分析
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
a1,a2,a3,a4,a5,...,an ,...
b1,b5,b9 , ..., ....
b13 ,
b17 ,
b4n-3 ,
解法2:(2)数列{an}的各项依次是数列{bn}的第1,5,9,13....项,
这些下标构成一个首项为1,公差为4的等差数列{cn}
则cn =4n-3.
令4n-3=29,解得n=8.
所以,b29是数列{an}的第8项.
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
典例分析
已知等差数列{an}的通项公式为an=4n-3,
则
(1)a1+a9= = a2+a8= =a3+a7= = 2a5= .
(2)a3+a15= = a5+a13= =a8+a10= = 2a9= .
34
34
34
17
34
66
66
66
33
66
猜想:等差数列{an},p,q,s,t,k∈N*,且p+q=s+t=2k,
则ap + aq = as + at= 2ak
计算
分析:只要根据等差数列的定义写出ap,aq,as,at,再利用已知条件即可得证。
证明:设数列{an}的公差为d,
则ap =a1+(p-1)d, aq =a1+(q-1)d,
as =a1+(s-1)d, at =a1+(t-1)d.
所以ap + aq =2a1+(p+q-2)d,
as + at =2a1+(s+t-2)d.
因为p+q=s+t,所以ap + aq = as + at.
例3.已知数列{an}是等差数列,p,q,s,t,∈N*,且p+q=s+t,则ap + aq = as + at
典例分析
例3是等差数列的一条性质,图4.2-2是它的一种情形.你能从几何角度解释等差数列的这一性质吗?
因为p+q=s+t, 所以ap + aq = as + at。
直线斜率相等
说明:
等差数列的性质:
注意:
对于此性质,必须是两项相加等于两项相加,否则不一定成立!
在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
巩固练习
(2)已知 a3+a11=10,求 a6+a7+a8
(3) 已知 a4+a5+a6+a7=56,a4a7=187,求a14及公差d.
分析:由 a1+a20 =a6+ a15 = a9 +a12 及 a6+a9+a12+a15=20,可得a1+a20=10。
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15。
分析: a4+a5+a6+a7=56 ,a4+a7=28 ,又 a4a7=187
解得
a4= 17
a7= 11
a4= 11
a7= 17
或
∴d= _2或2, 从而a14= _3或31。
典例分析
典例分析
等差数列的设项方法和技巧
(1)当已知条件中出现与首项、公差有关的内容时,可直接设首项为a1,公差为d,利用已知条件建立方程(组)求出a1和d,即可确定此等差数列的通项公式.
(2)当已知数列有3项时,可设为a-d,a,a+d,此时公差为d.若有5项、7项、…时,可同理设出.
(3)当已知数列有4项时,可设为a-3d,a-d,a+d,a+3d,此时公差为2d.若有6项、8项、…时,可同理设出.
规律总结:
d
cd
2d
等差数列
等差数列的性质推广
补充作业
1.等差数列{an}的前三项依次为 a-6,2a -5,-3a +2,则 a 等于( )
A . -1 B . 1 C .-2 D. 2
2.三数成等差数列,它们的和为12,首尾二数的积为12 ,求此三数.
3. 在等差数列{an}中, a1=83,a4=98,则这个数列有多少项在300到500之间?
4.已知数列{an} 的通项公式为 ,
问数列从第几项开始小于0?
请同学们回顾本节课的学习内容,并回答下列问题:
1.本节课学习的等差数列的性质有哪些?
2. 在解决问题时,用到了哪些数学思想?
课堂小结
数学与生活实际有着密切联系,数学概念来源于生活实际,又应用于生活实际。
4.2.1等差数列的概念
(第二课时)
1.等差数列的定义:
4.等差数列的函数特征:
3.等差数列的通项公式:
2.等差中项的定义:
函数图象上所有的点在同一条直线上:
d>0,等差数列单调增;d<0,等差数列单调减;
d=0,等差数列为常函数.
如果在 与 中间插入一个数A,使 ,A, 成等差数列,那么A叫做 与 的等差中项.
an=am+(n-m)d
累加法
an=a1+(n-1)d=dn+(a1-d),
f(x)=dx+(a1-d)
复习回顾
5.等差数列的判定方法:
定义法
知识加深
1.在等差数列{an}中
(1) 若a59=70,a80=112,求a101;
(2) 若ap=q,aq=p (p≠q),求ap+q;
(3) 若a12=20,a42=140, 求a10, a27
例1.
解:
知识应用
典例分析
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:a1,a2,a3,a4,a5,...
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
典例分析
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
解:(1)设数列{bn}的公差为d′.
由题意可知,b1=a1,b5=a2,于是b5-b1=a2-a1=8.
∵b5-b1=4d′,所以4d′ =8,所以d′ =2.
∴bn=2+(n-1)×2=2n
∴数列{bn}的通项公式是bn=2n.
典例分析
分析:(2)①先求b29=?
②再求an
③令an= ,解出n
解法1:(2)由(1)可得b29=2×29=58
因为a1=2,d=8 所以an=8n-6
令8n-6=58 解得n=8
所以b29是数列{an}项,是第8项。
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
典例分析
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
a1,a2,a3,a4,a5,...,an ,...
b1,b5,b9 , ..., ....
b13 ,
b17 ,
b4n-3 ,
解法2:(2)数列{an}的各项依次是数列{bn}的第1,5,9,13....项,
这些下标构成一个首项为1,公差为4的等差数列{cn}
则cn =4n-3.
令4n-3=29,解得n=8.
所以,b29是数列{an}的第8项.
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
典例分析
已知等差数列{an}的通项公式为an=4n-3,
则
(1)a1+a9= = a2+a8= =a3+a7= = 2a5= .
(2)a3+a15= = a5+a13= =a8+a10= = 2a9= .
34
34
34
17
34
66
66
66
33
66
猜想:等差数列{an},p,q,s,t,k∈N*,且p+q=s+t=2k,
则ap + aq = as + at= 2ak
计算
分析:只要根据等差数列的定义写出ap,aq,as,at,再利用已知条件即可得证。
证明:设数列{an}的公差为d,
则ap =a1+(p-1)d, aq =a1+(q-1)d,
as =a1+(s-1)d, at =a1+(t-1)d.
所以ap + aq =2a1+(p+q-2)d,
as + at =2a1+(s+t-2)d.
因为p+q=s+t,所以ap + aq = as + at.
例3.已知数列{an}是等差数列,p,q,s,t,∈N*,且p+q=s+t,则ap + aq = as + at
典例分析
例3是等差数列的一条性质,图4.2-2是它的一种情形.你能从几何角度解释等差数列的这一性质吗?
因为p+q=s+t, 所以ap + aq = as + at。
直线斜率相等
说明:
等差数列的性质:
注意:
对于此性质,必须是两项相加等于两项相加,否则不一定成立!
在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
巩固练习
(2)已知 a3+a11=10,求 a6+a7+a8
(3) 已知 a4+a5+a6+a7=56,a4a7=187,求a14及公差d.
分析:由 a1+a20 =a6+ a15 = a9 +a12 及 a6+a9+a12+a15=20,可得a1+a20=10。
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15。
分析: a4+a5+a6+a7=56 ,a4+a7=28 ,又 a4a7=187
解得
a4= 17
a7= 11
a4= 11
a7= 17
或
∴d= _2或2, 从而a14= _3或31。
典例分析
典例分析
等差数列的设项方法和技巧
(1)当已知条件中出现与首项、公差有关的内容时,可直接设首项为a1,公差为d,利用已知条件建立方程(组)求出a1和d,即可确定此等差数列的通项公式.
(2)当已知数列有3项时,可设为a-d,a,a+d,此时公差为d.若有5项、7项、…时,可同理设出.
(3)当已知数列有4项时,可设为a-3d,a-d,a+d,a+3d,此时公差为2d.若有6项、8项、…时,可同理设出.
规律总结:
d
cd
2d
等差数列
等差数列的性质推广
补充作业
1.等差数列{an}的前三项依次为 a-6,2a -5,-3a +2,则 a 等于( )
A . -1 B . 1 C .-2 D. 2
2.三数成等差数列,它们的和为12,首尾二数的积为12 ,求此三数.
3. 在等差数列{an}中, a1=83,a4=98,则这个数列有多少项在300到500之间?
4.已知数列{an} 的通项公式为 ,
问数列从第几项开始小于0?
请同学们回顾本节课的学习内容,并回答下列问题:
1.本节课学习的等差数列的性质有哪些?
2. 在解决问题时,用到了哪些数学思想?
课堂小结
数学与生活实际有着密切联系,数学概念来源于生活实际,又应用于生活实际。
