4-2-2等差数列的前n项和公式(第一课时) 课件(共21张PPT)
文档属性
| 名称 | 4-2-2等差数列的前n项和公式(第一课时) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 995.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 07:25:10 | ||
图片预览







文档简介
4.2.2 等差数列的前n项和公式
(第一课时)
创设情景
古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数。他们研究过三角形数1,3,6,10,15, … ,如图所示,这个图案中有n层。
如果图中的石子有100层,那么第1层到第100层一共用了多少粒石子?
即求 1+2+3+…+100=?
这就是历史上著名的“高斯的算法”,也就是首尾配对法,通过过配对凑成相同数,变“多步求和”为“一步相乘”!
高斯的算法实际上解决了求等差数列
1,2,3,…,n,… ①
前100项和的问题。
如果图中的石子有101层,那么第1层到第101层一共用了多少粒石子?
追问1:
新知探究
即求 1+2+3+…+100+101=?
你能用“高斯算法”求和吗?
这是求奇数个项的和的问题,若简单地模仿“高斯算法”,将会出现不能全部配对的问题,会多出一项或者说少了一项,这就是高斯算法的不足之处,在求和问题中需要进行奇偶数项的讨论.
(1)n为偶数时:
(2)n为奇数时:
记
=
?
将上述方法推广到一般,可以得到:
(可拿出中间项或末项,用“高斯算法”入手探求)
追问2:
是否一定要分类讨论?能否设法避开分类讨论实现配对,将不同数的求和转化为相同数的求和?
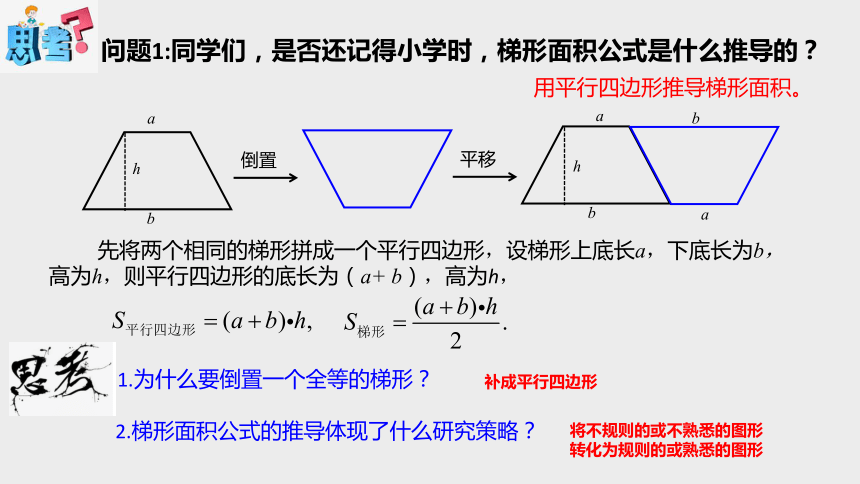
问题1:同学们,是否还记得小学时,梯形面积公式是什么推导的?
先将两个相同的梯形拼成一个平行四边形,设梯形上底长a,下底长为b,高为h,则平行四边形的底长为(a+ b),高为h,
用平行四边形推导梯形面积。
倒置
平移
a
b
h
a
b
a
b
h
1.为什么要倒置一个全等的梯形?
2.梯形面积公式的推导体现了什么研究策略?
补成平行四边形
将不规则的或不熟悉的图形转化为规则的或熟悉的图形
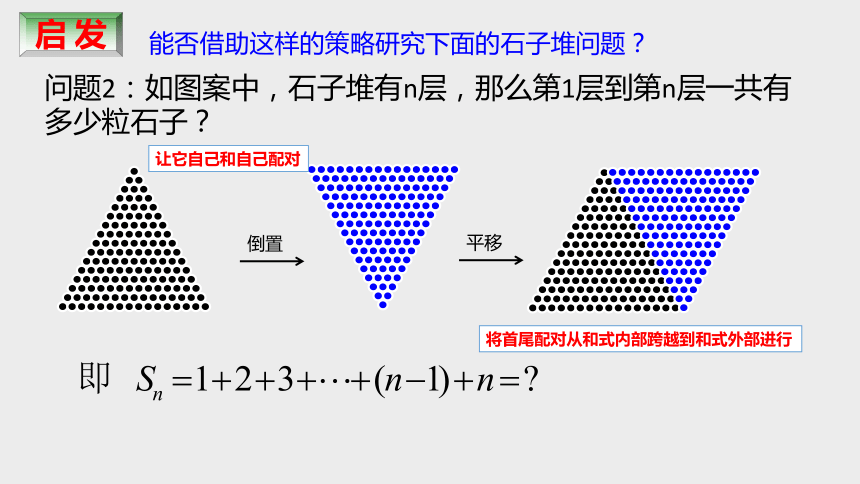
问题2:如图案中,石子堆有n层,那么第1层到第n层一共有多少粒石子?
启 发
能否借助这样的策略研究下面的石子堆问题?
倒置
平移
让它自己和自己配对
将首尾配对从和式内部跨越到和式外部进行
所以,要求 Sn=1+2+3+…+n,我们可以把和倒过再写一个式子, Sn=n+(n-1)+(n-2)+…+2+1 ,将首尾配对从和式内部跨越到和式外部进行,将两个和式配对就可以避免分类讨论的麻烦.
分析:这其实是求一个具体的等差数列前n项和.
问题3:
由上述方法得到启示,用倒序相加法求.
如何才能将等式的右边化简?
公式变形
如何根据公式的结构特征来记忆公式呢?
含a1 和an
含a1 和d
等差数列的通项公式和前n项和公式中,共有“a1,d ,n,an,Sn”五个
量,故知三可求其二.
结合梯形的面积公式来记忆等差数列前 n 项和公式
(等腰梯形的面积=平行四边形面积+三角形面积)
公式记忆
等差数列前 n 项和公式
选用公式
变用公式
知三求二
(1)
(2)
不从公式(1)出发,你能用其他方法得到公式(2)吗?
解: (1) ????????????=????????(????????+????????????)????
?
=????????(????+????????????)????
?
=????????????????
?
(2) ????=????????-????????=????????-2=????????
?
????????????=????????????????+????????×????????d
?
=???????? ×?2+????????×???????? ×????????
?
=????????????
?
公式应用
选用公式
变用公式
知三求二
例1
解: (3)由????????=????????????+????×(?????????)????d,得
?
整理,得
????????-7n-60=0
?
?????=????????n+????×(?????????)???? ×(?????????)
?
解得
n=12或n=-5(舍去)
所以
n=12
选用公式
变用公式
知三求二
例1
巩固练习
例2 已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的首项和公差吗?
解:由题意知:S10=310,S20=1220,将它们代入公式
得到
还有其它方法吗?
方程思想
例题讲解
例2 已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的首项和公差吗?
一题多解
例2变式、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的前30项和吗?
由例2,可知
【解】
例2变式、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的前30项和吗?
【另解】由等差数列的性质,可推得:
成等差数列
解得前30项的和为2730 .
说明:
1.上述方法没有列出方程求出具体的个别量,而是恰当地运用数学中的整体思想来快速求出,要注意体会这种思想在数学中的运用.
2.等差数列被均匀分段求和后,得到的数列仍是等差数列
变式提高
整体思想
一般地,在等差数列{an}中,有S2n-1=(2n-1)an.
解析 在等差数列中,S6,S12-S6,S18-S12成等差数列,
∵S6=1,S12=4,∴1,3,S18-4成公差为2的等差数列,
即S18-4=5,∴S18=9.
1.设Sn为等差数列{an}的前n项和,若S6=1,S12=4,则S18=________.
巩固练习
解析 由题知a2+a8+a11=a1+d+a1+7d+a1+10d
=3a1+18d =3(a1+6d) =3a7,
2.(多选)(2022·淄博调研)已知等差数列{an}的公差为d,前n项和为Sn,当首项a1和d变化时,a2+a8+a11是一个定值,则下列各数也为定值的是( )
A.a7 B.a8 C.S13 D.S15
回顾从特殊到一般的研究方法;
体会等差数列的基本元表示方法,倒序相加的算法,及数形结合的数学思想;
掌握等差数列的两个求和公式及简单应用。
课堂小结
(第一课时)
创设情景
古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数。他们研究过三角形数1,3,6,10,15, … ,如图所示,这个图案中有n层。
如果图中的石子有100层,那么第1层到第100层一共用了多少粒石子?
即求 1+2+3+…+100=?
这就是历史上著名的“高斯的算法”,也就是首尾配对法,通过过配对凑成相同数,变“多步求和”为“一步相乘”!
高斯的算法实际上解决了求等差数列
1,2,3,…,n,… ①
前100项和的问题。
如果图中的石子有101层,那么第1层到第101层一共用了多少粒石子?
追问1:
新知探究
即求 1+2+3+…+100+101=?
你能用“高斯算法”求和吗?
这是求奇数个项的和的问题,若简单地模仿“高斯算法”,将会出现不能全部配对的问题,会多出一项或者说少了一项,这就是高斯算法的不足之处,在求和问题中需要进行奇偶数项的讨论.
(1)n为偶数时:
(2)n为奇数时:
记
=
?
将上述方法推广到一般,可以得到:
(可拿出中间项或末项,用“高斯算法”入手探求)
追问2:
是否一定要分类讨论?能否设法避开分类讨论实现配对,将不同数的求和转化为相同数的求和?
问题1:同学们,是否还记得小学时,梯形面积公式是什么推导的?
先将两个相同的梯形拼成一个平行四边形,设梯形上底长a,下底长为b,高为h,则平行四边形的底长为(a+ b),高为h,
用平行四边形推导梯形面积。
倒置
平移
a
b
h
a
b
a
b
h
1.为什么要倒置一个全等的梯形?
2.梯形面积公式的推导体现了什么研究策略?
补成平行四边形
将不规则的或不熟悉的图形转化为规则的或熟悉的图形
问题2:如图案中,石子堆有n层,那么第1层到第n层一共有多少粒石子?
启 发
能否借助这样的策略研究下面的石子堆问题?
倒置
平移
让它自己和自己配对
将首尾配对从和式内部跨越到和式外部进行
所以,要求 Sn=1+2+3+…+n,我们可以把和倒过再写一个式子, Sn=n+(n-1)+(n-2)+…+2+1 ,将首尾配对从和式内部跨越到和式外部进行,将两个和式配对就可以避免分类讨论的麻烦.
分析:这其实是求一个具体的等差数列前n项和.
问题3:
由上述方法得到启示,用倒序相加法求.
如何才能将等式的右边化简?
公式变形
如何根据公式的结构特征来记忆公式呢?
含a1 和an
含a1 和d
等差数列的通项公式和前n项和公式中,共有“a1,d ,n,an,Sn”五个
量,故知三可求其二.
结合梯形的面积公式来记忆等差数列前 n 项和公式
(等腰梯形的面积=平行四边形面积+三角形面积)
公式记忆
等差数列前 n 项和公式
选用公式
变用公式
知三求二
(1)
(2)
不从公式(1)出发,你能用其他方法得到公式(2)吗?
解: (1) ????????????=????????(????????+????????????)????
?
=????????(????+????????????)????
?
=????????????????
?
(2) ????=????????-????????=????????-2=????????
?
????????????=????????????????+????????×????????d
?
=???????? ×?2+????????×???????? ×????????
?
=????????????
?
公式应用
选用公式
变用公式
知三求二
例1
解: (3)由????????=????????????+????×(?????????)????d,得
?
整理,得
????????-7n-60=0
?
?????=????????n+????×(?????????)???? ×(?????????)
?
解得
n=12或n=-5(舍去)
所以
n=12
选用公式
变用公式
知三求二
例1
巩固练习
例2 已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的首项和公差吗?
解:由题意知:S10=310,S20=1220,将它们代入公式
得到
还有其它方法吗?
方程思想
例题讲解
例2 已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的首项和公差吗?
一题多解
例2变式、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的前30项和吗?
由例2,可知
【解】
例2变式、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的前30项和吗?
【另解】由等差数列的性质,可推得:
成等差数列
解得前30项的和为2730 .
说明:
1.上述方法没有列出方程求出具体的个别量,而是恰当地运用数学中的整体思想来快速求出,要注意体会这种思想在数学中的运用.
2.等差数列被均匀分段求和后,得到的数列仍是等差数列
变式提高
整体思想
一般地,在等差数列{an}中,有S2n-1=(2n-1)an.
解析 在等差数列中,S6,S12-S6,S18-S12成等差数列,
∵S6=1,S12=4,∴1,3,S18-4成公差为2的等差数列,
即S18-4=5,∴S18=9.
1.设Sn为等差数列{an}的前n项和,若S6=1,S12=4,则S18=________.
巩固练习
解析 由题知a2+a8+a11=a1+d+a1+7d+a1+10d
=3a1+18d =3(a1+6d) =3a7,
2.(多选)(2022·淄博调研)已知等差数列{an}的公差为d,前n项和为Sn,当首项a1和d变化时,a2+a8+a11是一个定值,则下列各数也为定值的是( )
A.a7 B.a8 C.S13 D.S15
回顾从特殊到一般的研究方法;
体会等差数列的基本元表示方法,倒序相加的算法,及数形结合的数学思想;
掌握等差数列的两个求和公式及简单应用。
课堂小结
