4-2-2等差数列的前n项和公式(第二课时) 课件(共21张PPT)
文档属性
| 名称 | 4-2-2等差数列的前n项和公式(第二课时) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 07:57:07 | ||
图片预览








文档简介
(共21张PPT)
4.2.2 等差数列的前n项和公式
(第二课时)
1.等差数列前n项和公式推导方法.
2.掌握等差数列前n项和公式的两种形式.
倒序相加法
Sn=a1+ a2+ a3+ …… + an
Sn=an+an-1+an-2+…… +a1
2Sn= (a1+an)+(a2+an-1)+(a3+an-2)+…… +(an +a1)
= n (a1+an)
an=a1+(n-1)d
复习回顾
解:
例1.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
学习新知
典型例题
当n≥2时,
当n=1时,
当n=1时也满足①式.
①
解:
典型例题
变式训练
当n >1时,
当n=1时,
当n=1时不满足①式.
分类讨论思想
①
● 如果一个数列{an}的前n项和为Sn=pn2+qm+r,其中p、q、r为常数,且p≠0,那么这个数列一定是等差数列吗?如果是,它的首项和公差是什么?
(1)若r=0,则这个数列一定是等差数列.
结论:数列是等差数列等价于
常数项为0的关于n的二次型函数
深化探究
(过原点)
(2)若r≠0,则这个数列一定不是等差数列.
典型例题
解:
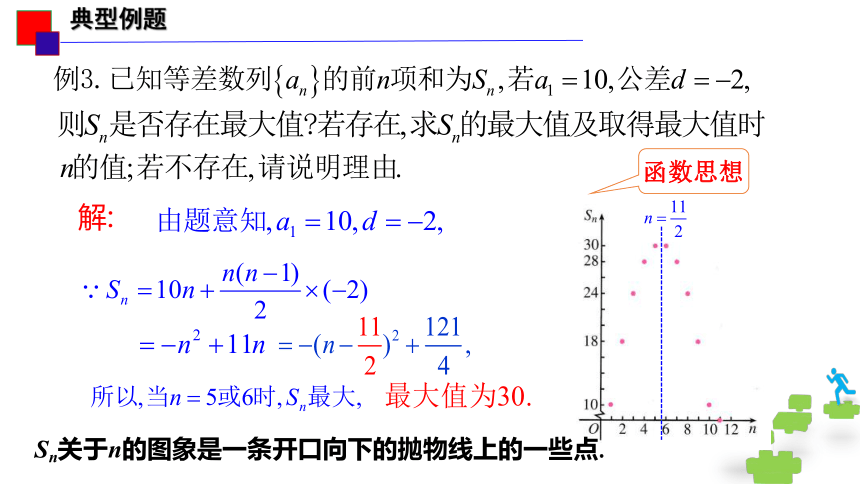
函数思想
Sn关于n的图象是一条开口向下的抛物线上的一些点.
典型例题
另解:
从等差数列的通项公式出发来分析
(1)利用an:
当a1>0,d<0,前n项和有最大值.
可由an≥0,且an+1 ≤0,求得n的值;
当a1<0,d>0,前n项和有最小值.
可由an≤0,且an+1≥0,求得n的值.
等差数列前项和的最值问题有两种常用的方法:
(2)利用Sn:
由 利用二次函数配方法求得最值时n的值.
归纳提升
解 法一 设公差为d.
练习. 等差数列{an}中,设Sn为其前n项和,且a1>0,S3=S11,则当n为多少时,Sn最大?
故当n=7时,Sn最大.
巩固训练
法二 易知Sn=An2+Bn是关于n的二次函数,
故当n=7时,Sn最大.
法四 设公差为d.由S3=S11,可得2a1+13d=0,
即(a1+6d)+(a1+7d)=0,故a7+a8=0,
又由a1>0,S3=S11可知d<0,
所以a7>0,a8<0,所以当n=7时,Sn最大.
解 ∵等差数列{an}中,公差d<0,a2+a6=-8,
∴a2+a6=a3+a5=-8,又∵a3a5=7,
∴a3,a5是一元二次方程x2+8x+7=0的两个根,且a3>a5,
解方程x2+8x+7=0,得a3=-1,a5=-7,
例4. 等差数列{an}中,公差d<0,a2+a6=-8,a3a5=7.
(1)求{an}的通项公式;
∴an=5+(n-1)×(-3)=-3n+8.
典型例题
(2)记Tn为数列{bn}前n项的和,其中bn=|an|,n∈N*,若Tn≥1 464,求n的最小值.
∵bn=|an|,∴b1=5,b2=2,b3=|-1|=1,b4=|-4|=4,
当n≥3时,bn=|an|=3n-8.
当n<3时,T1=5,T2=7;
∴n的最小值为34.
证明:
典型例题
再探.
再探.
蓦然回首
这节课我的收获是什么?
课堂小结
反之如何证明?
当m=n时,公式变化?
请证明公式!
课后探究
(3)已知等差数列{an}的项数为奇数,其中所有奇数项之和 为319,所有偶数项之和为290,则该数列的中间项为( ) A. 28 B.29 C.30 D.31
相应练习
4.2.2 等差数列的前n项和公式
(第二课时)
1.等差数列前n项和公式推导方法.
2.掌握等差数列前n项和公式的两种形式.
倒序相加法
Sn=a1+ a2+ a3+ …… + an
Sn=an+an-1+an-2+…… +a1
2Sn= (a1+an)+(a2+an-1)+(a3+an-2)+…… +(an +a1)
= n (a1+an)
an=a1+(n-1)d
复习回顾
解:
例1.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
学习新知
典型例题
当n≥2时,
当n=1时,
当n=1时也满足①式.
①
解:
典型例题
变式训练
当n >1时,
当n=1时,
当n=1时不满足①式.
分类讨论思想
①
● 如果一个数列{an}的前n项和为Sn=pn2+qm+r,其中p、q、r为常数,且p≠0,那么这个数列一定是等差数列吗?如果是,它的首项和公差是什么?
(1)若r=0,则这个数列一定是等差数列.
结论:数列是等差数列等价于
常数项为0的关于n的二次型函数
深化探究
(过原点)
(2)若r≠0,则这个数列一定不是等差数列.
典型例题
解:
函数思想
Sn关于n的图象是一条开口向下的抛物线上的一些点.
典型例题
另解:
从等差数列的通项公式出发来分析
(1)利用an:
当a1>0,d<0,前n项和有最大值.
可由an≥0,且an+1 ≤0,求得n的值;
当a1<0,d>0,前n项和有最小值.
可由an≤0,且an+1≥0,求得n的值.
等差数列前项和的最值问题有两种常用的方法:
(2)利用Sn:
由 利用二次函数配方法求得最值时n的值.
归纳提升
解 法一 设公差为d.
练习. 等差数列{an}中,设Sn为其前n项和,且a1>0,S3=S11,则当n为多少时,Sn最大?
故当n=7时,Sn最大.
巩固训练
法二 易知Sn=An2+Bn是关于n的二次函数,
故当n=7时,Sn最大.
法四 设公差为d.由S3=S11,可得2a1+13d=0,
即(a1+6d)+(a1+7d)=0,故a7+a8=0,
又由a1>0,S3=S11可知d<0,
所以a7>0,a8<0,所以当n=7时,Sn最大.
解 ∵等差数列{an}中,公差d<0,a2+a6=-8,
∴a2+a6=a3+a5=-8,又∵a3a5=7,
∴a3,a5是一元二次方程x2+8x+7=0的两个根,且a3>a5,
解方程x2+8x+7=0,得a3=-1,a5=-7,
例4. 等差数列{an}中,公差d<0,a2+a6=-8,a3a5=7.
(1)求{an}的通项公式;
∴an=5+(n-1)×(-3)=-3n+8.
典型例题
(2)记Tn为数列{bn}前n项的和,其中bn=|an|,n∈N*,若Tn≥1 464,求n的最小值.
∵bn=|an|,∴b1=5,b2=2,b3=|-1|=1,b4=|-4|=4,
当n≥3时,bn=|an|=3n-8.
当n<3时,T1=5,T2=7;
∴n的最小值为34.
证明:
典型例题
再探.
再探.
蓦然回首
这节课我的收获是什么?
课堂小结
反之如何证明?
当m=n时,公式变化?
请证明公式!
课后探究
(3)已知等差数列{an}的项数为奇数,其中所有奇数项之和 为319,所有偶数项之和为290,则该数列的中间项为( ) A. 28 B.29 C.30 D.31
相应练习
