4-3-1等比数列的概念(第一课时) 课件(共29张PPT)
文档属性
| 名称 | 4-3-1等比数列的概念(第一课时) 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 07:58:09 | ||
图片预览








文档简介
(共29张PPT)
(第一课时)
4.3 等比数列的概念
1.等差数列的定义:
3.等差数列的通项公式:
2.等差中项的定义:
an=am+(n-m)d
如果在 a与b中间插入一个数A,使a ,A,b成等差数列,那么A叫做a与b 的等差中项,
不完全归纳法、累加法
复习回顾
如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,这个数列就叫做等差数列.
符号表示: an - an-1=d(n≥2,n∈N*)或 an+1 - an=d(n∈N*)
4.等差数列的函数特征:
图象是均匀分布在直线f(x)=dx+(a1-d)上的点:
d>0,等差数列单调增;d<0,等差数列单调减;
d=0,等差数列为常函数.
an=a1+(n-1)d=dn+(a1-d),
5.等差数列的判定方法:
①定义法
②中项法
类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
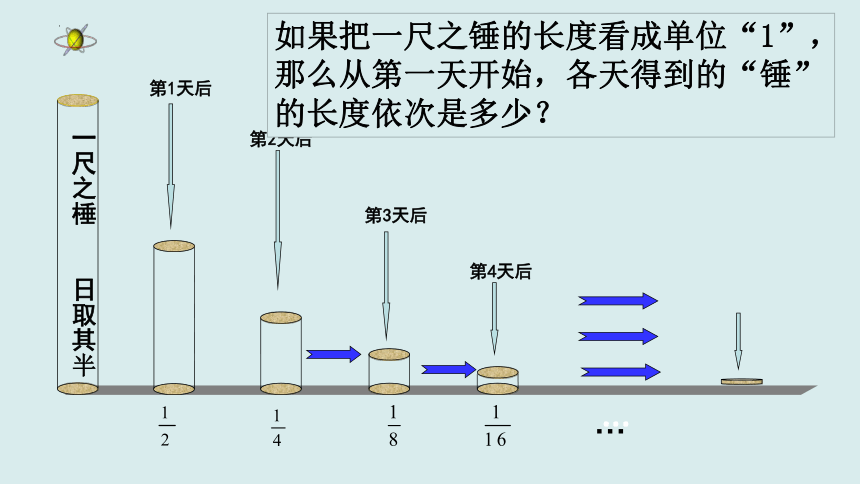
1.《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
情景导学
...
一尺之棰 日取其半
第1天后
第2天后
第3天后
第4天后
如果把一尺之锤的长度看成单位“1”,那么从第一天开始,各天得到的“锤”的长度依次是多少?
…
2. 两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
3.某人存入银行a元,存期为五年,年利率为r,那么按照复利,他五年内每年末得到的本利和分别是
(复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息)
a(1+r),a(1+r)2,a(1+r)3,a(1+r)4,a(1+r)5
新知探究
观察前面得到的数列,看看他们有什么共同的特点?
(1)
(2)9,92,93,...,910;
(3)100,1002,1003,...,10010;
(4)5,52,...,510
(5)a(1+r),a(1+r)2,a(1+r)3,a(1+r)4,a(1+r)5
从第2项起,每一项与前一项的比都等于同一常数.
共同特点:
1. 等比数列的定义
类比等差数列的概念,从上述几个数你能抽象出等比数列的概念吗?
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列 ,这个常数叫做等比数列的公比,公比通常用字母q表示(显然q ≠ 0 ) 。
咬文嚼字
符号表示:
追问1.等比数列的定义中,“q≠0”的原因是什么?
结合等差数列的定义式,将等比数列的文字定义转化为数学符号语言。
追问2.如果一个数列是等比数列,它至少有几项?
(1) 1,3,9,27,81,…
(3) 5,5,5,5,5,5,…
(4) 1,-1,1,-1,1,…
是,公比 q=3
是,公比 q= x
是,公 比q= -1
(7)
(2)
是,公比 q=
练习.观察并判断下列数列是否是等比数列,若是,指出公比.
是,公比 q=1
(5) 1,0,1,0,1,…
(6) 0,0,0,0,0,…
不是等比数列
不是等比数列
巩固练习
1.公比q是每一项(第2项起)与它的前一项的比,防止把 被除数与除数弄颠倒。
2.公比q可以是正数,负数,可以是1,但不可以为0。当q>0,各项与首项同号;当q<0,各项符号正负相间。
3.等比数列中各项均不能为0,即an ≠ 0。
4.非零的常数列既是等差数列又是等比数列。
2. 等比中项
请同学们类比等差中项的推导过程,探究等比中项及其性质.
由三个数a,G,b组成等比数列,那么G叫做a与b的等比中项.
此时,
(an)2=an-1.an+1
在一个等比数列中,从第2项起,每一项(有穷数列的末项除外)都是它前一项与后一项的等比中项.
观察如下的两个数之间,插入一个什么数后三个数就会成为一个等比数列:
(1) 1, , 9 (2)-1, , -4
(3) -12, ,-3 (4)-1, , 16
练一练
同号两数则有两个等比中项,它们互为相反数;
异号两数则没有等比中项.
(n-1)个
式子
… …
方法二:(累加法)
… …
方法一:(不完全归纳法)
等差数列的通项公式的具体推导过程和方法。
请同学们类比等差数列通项公式的推导方法,推导出等比数列的通项公式。
3. 等比通项公式
… …
方法一:不完全归纳法
1
1
-
=
n
n
q
a
a
(n-1)个
式子
方法二:累乘法
验证 n=1
3. 等比通项公式
当q=1时,这是一个常数列, an ≠ 0。
等比数列{an} ,首项为a1,公比为q , 它的通项公式为
注:方程中有四个量,知三求一,这是公式最简单的应用。
小试牛刀
在等差数列 {an}中
试问:在等比数列{an}中,如果知道an和公比q,能否求am?如果能,请写出表达式。
通项变形
4. 等比数列与指数函数的关系
探究:在等差数列中,公差d ≠ 0的等差数列可以与相应的一次函数建立联系,那么对于等比数列,公比q满足什么条件的数列可以与相应的指数函数建立类似的关系?
例1 在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
典例分析
例1 在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
典例分析
等比数列通项公式的求法
a1和q是等比数列的基本量,只要求出这两个基本量,问题便迎刃而解.关于a1和q的求法通常有以下两种方法:
(1)根据已知条件,建立关于a1,q的方程组,求出a1,q后再求an,这是常规方法.
(2)充分利用各项之间的关系,直接求出q后,再求a1,最后求an,这种方法带有一定的技巧性,能简化运算.
例2 数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132,求这个数列.
典例分析
解:
练习 有四个数,前三个数成等比数列,后三个数成等差数列,第一个数与第四个数的和为21,中间两个数的和为18,求这四个数.
分析:三个数成等比数列,可怎么设为?
例3 已知数列{an} , {bn} 是项数相同的等比数列,那么数列 {an ●bn}是等比数列吗?
典例分析
练习 已知数列{an}满足a1=1,an+1=2an+1.
证明:数列{an+1}是等比数列.
1)等比数列的定义是什么?怎样判断一个数列是否是等比数列?
2)等比数列得通项公式是?其中每个字母所代表的含义是什么?
3)等比数列应注意哪些问题?
【小结】说说你的收获。
课堂小结
类比等差数列的性质,探究等比数列的性质。
课后探究
(第一课时)
4.3 等比数列的概念
1.等差数列的定义:
3.等差数列的通项公式:
2.等差中项的定义:
an=am+(n-m)d
如果在 a与b中间插入一个数A,使a ,A,b成等差数列,那么A叫做a与b 的等差中项,
不完全归纳法、累加法
复习回顾
如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,这个数列就叫做等差数列.
符号表示: an - an-1=d(n≥2,n∈N*)或 an+1 - an=d(n∈N*)
4.等差数列的函数特征:
图象是均匀分布在直线f(x)=dx+(a1-d)上的点:
d>0,等差数列单调增;d<0,等差数列单调减;
d=0,等差数列为常函数.
an=a1+(n-1)d=dn+(a1-d),
5.等差数列的判定方法:
①定义法
②中项法
类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
1.《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
情景导学
...
一尺之棰 日取其半
第1天后
第2天后
第3天后
第4天后
如果把一尺之锤的长度看成单位“1”,那么从第一天开始,各天得到的“锤”的长度依次是多少?
…
2. 两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
3.某人存入银行a元,存期为五年,年利率为r,那么按照复利,他五年内每年末得到的本利和分别是
(复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息)
a(1+r),a(1+r)2,a(1+r)3,a(1+r)4,a(1+r)5
新知探究
观察前面得到的数列,看看他们有什么共同的特点?
(1)
(2)9,92,93,...,910;
(3)100,1002,1003,...,10010;
(4)5,52,...,510
(5)a(1+r),a(1+r)2,a(1+r)3,a(1+r)4,a(1+r)5
从第2项起,每一项与前一项的比都等于同一常数.
共同特点:
1. 等比数列的定义
类比等差数列的概念,从上述几个数你能抽象出等比数列的概念吗?
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列 ,这个常数叫做等比数列的公比,公比通常用字母q表示(显然q ≠ 0 ) 。
咬文嚼字
符号表示:
追问1.等比数列的定义中,“q≠0”的原因是什么?
结合等差数列的定义式,将等比数列的文字定义转化为数学符号语言。
追问2.如果一个数列是等比数列,它至少有几项?
(1) 1,3,9,27,81,…
(3) 5,5,5,5,5,5,…
(4) 1,-1,1,-1,1,…
是,公比 q=3
是,公比 q= x
是,公 比q= -1
(7)
(2)
是,公比 q=
练习.观察并判断下列数列是否是等比数列,若是,指出公比.
是,公比 q=1
(5) 1,0,1,0,1,…
(6) 0,0,0,0,0,…
不是等比数列
不是等比数列
巩固练习
1.公比q是每一项(第2项起)与它的前一项的比,防止把 被除数与除数弄颠倒。
2.公比q可以是正数,负数,可以是1,但不可以为0。当q>0,各项与首项同号;当q<0,各项符号正负相间。
3.等比数列中各项均不能为0,即an ≠ 0。
4.非零的常数列既是等差数列又是等比数列。
2. 等比中项
请同学们类比等差中项的推导过程,探究等比中项及其性质.
由三个数a,G,b组成等比数列,那么G叫做a与b的等比中项.
此时,
(an)2=an-1.an+1
在一个等比数列中,从第2项起,每一项(有穷数列的末项除外)都是它前一项与后一项的等比中项.
观察如下的两个数之间,插入一个什么数后三个数就会成为一个等比数列:
(1) 1, , 9 (2)-1, , -4
(3) -12, ,-3 (4)-1, , 16
练一练
同号两数则有两个等比中项,它们互为相反数;
异号两数则没有等比中项.
(n-1)个
式子
… …
方法二:(累加法)
… …
方法一:(不完全归纳法)
等差数列的通项公式的具体推导过程和方法。
请同学们类比等差数列通项公式的推导方法,推导出等比数列的通项公式。
3. 等比通项公式
… …
方法一:不完全归纳法
1
1
-
=
n
n
q
a
a
(n-1)个
式子
方法二:累乘法
验证 n=1
3. 等比通项公式
当q=1时,这是一个常数列, an ≠ 0。
等比数列{an} ,首项为a1,公比为q , 它的通项公式为
注:方程中有四个量,知三求一,这是公式最简单的应用。
小试牛刀
在等差数列 {an}中
试问:在等比数列{an}中,如果知道an和公比q,能否求am?如果能,请写出表达式。
通项变形
4. 等比数列与指数函数的关系
探究:在等差数列中,公差d ≠ 0的等差数列可以与相应的一次函数建立联系,那么对于等比数列,公比q满足什么条件的数列可以与相应的指数函数建立类似的关系?
例1 在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
典例分析
例1 在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
典例分析
等比数列通项公式的求法
a1和q是等比数列的基本量,只要求出这两个基本量,问题便迎刃而解.关于a1和q的求法通常有以下两种方法:
(1)根据已知条件,建立关于a1,q的方程组,求出a1,q后再求an,这是常规方法.
(2)充分利用各项之间的关系,直接求出q后,再求a1,最后求an,这种方法带有一定的技巧性,能简化运算.
例2 数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132,求这个数列.
典例分析
解:
练习 有四个数,前三个数成等比数列,后三个数成等差数列,第一个数与第四个数的和为21,中间两个数的和为18,求这四个数.
分析:三个数成等比数列,可怎么设为?
例3 已知数列{an} , {bn} 是项数相同的等比数列,那么数列 {an ●bn}是等比数列吗?
典例分析
练习 已知数列{an}满足a1=1,an+1=2an+1.
证明:数列{an+1}是等比数列.
1)等比数列的定义是什么?怎样判断一个数列是否是等比数列?
2)等比数列得通项公式是?其中每个字母所代表的含义是什么?
3)等比数列应注意哪些问题?
【小结】说说你的收获。
课堂小结
类比等差数列的性质,探究等比数列的性质。
课后探究
