相似全程测评
图片预览



文档简介
【闯关磨练】
〖基础训练〗
1.位似图形上某一对对应点到位似中心的距离分别是10cm和5cm,则他们的位似比是___________.
【考点分析】考查位似比的概念.
【名师点评】位似比即位似图形的相似比,亦为对应点到位似中心的距离比.
【正确答案】2
2.下列判断中,正确的是( )
A.相似图形一定是位似图形.
B.位似图形一定是相似图形.
C.全等的图形一定是位似图形.
D.位似图形一定是全等图形.
【考点分析】考查相似图形、位似图形、全等图形之间的关系.
【名师点评】
位似图形是相似图形的一种特殊情况,所以位似图形肯定是相似图形,而相似图形不一定是位似图形;全等又是相似的特殊情况,与位似没有直接联系,全等的图形不一定是位似图形,位似图形也不一定是全等图形.
【正确答案】 B
3.若两个图形位似,则下列叙述不正确的是( )
A.每对对应点所在的直线相交于同一点.
B.两个图形上的对应线段之比等于位似比.
C.两个图形上的对应线段必平行.
D.两个图形的面积之比等于位似比的平方.
【考点分析】考查两个位似图形之间的关系.
【名师点评】
由位似图形的定义可知,两个图形位似必须符合三个条件:①相似,②对应边平行或在同一直线上,③对应顶点的连线交与一点.对应线段有可能在同一直线上,所以选项C错误.
【正确答案】C
4.用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
A.只能选在原图形的外部.
B.只能选在原图形的内部.
C.只能选在原图形的边上.
D.可以选择任意位置.
【考点分析】考查位似中心的概念.
【名师点评】位似图形的位似中心可以选择平面内的任意位置.
【正确答案】D
5.△OCD与△OAB是位似图形,其中位似比为2∶3,若将两个图形放大,使放大前后对应线段的比为1∶2,则放大后两个三角形的位似比为( ).
A.4∶3 B.1∶3 C.2∶3 D.1∶2
【考点分析】考查位似比与相似比的关系.
【名师点评】
位似比即位似图形的相似比,亦为对应点到位似中心的距离比,相似比为相似图形对应边的比,△OCD与△OAB都放大2倍后相似比不变.
【正确答案】C
6.在如图所示的四个图案中的两个图形可以看作是位似变换得到的是( ).
A.(1)(2) B.(1)(3) C.(3)(4) D.(1)(4)
【考点分析】考查位似图形的判断.
【名师点评】
位似图形的判断要根据定义,须符合三个条件:①相似,②对应边平行或在同一直线上,③对应顶点的连线交与一点.
【正确答案】D
7.平面直角坐标系中,有一条鱼,它有六个顶点,下列说法中正确的是( )
A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似.
B.将各点纵坐标乘以2, 横坐标不变,得到的鱼与原来的鱼位似.
C.将各点横、纵坐标都乘以2,得到的鱼与原来的鱼位似.
D.将各点横坐标乘以2,纵坐标乘以,得到的鱼与原来的鱼位似.
【考点分析】考查以原点为位似中心,两位似图形坐标之间的关系.
【名师点评】
平面直角坐标系中,以原点为位似中心,两位似图形横、纵坐标之比都为或-.
【正确答案】C
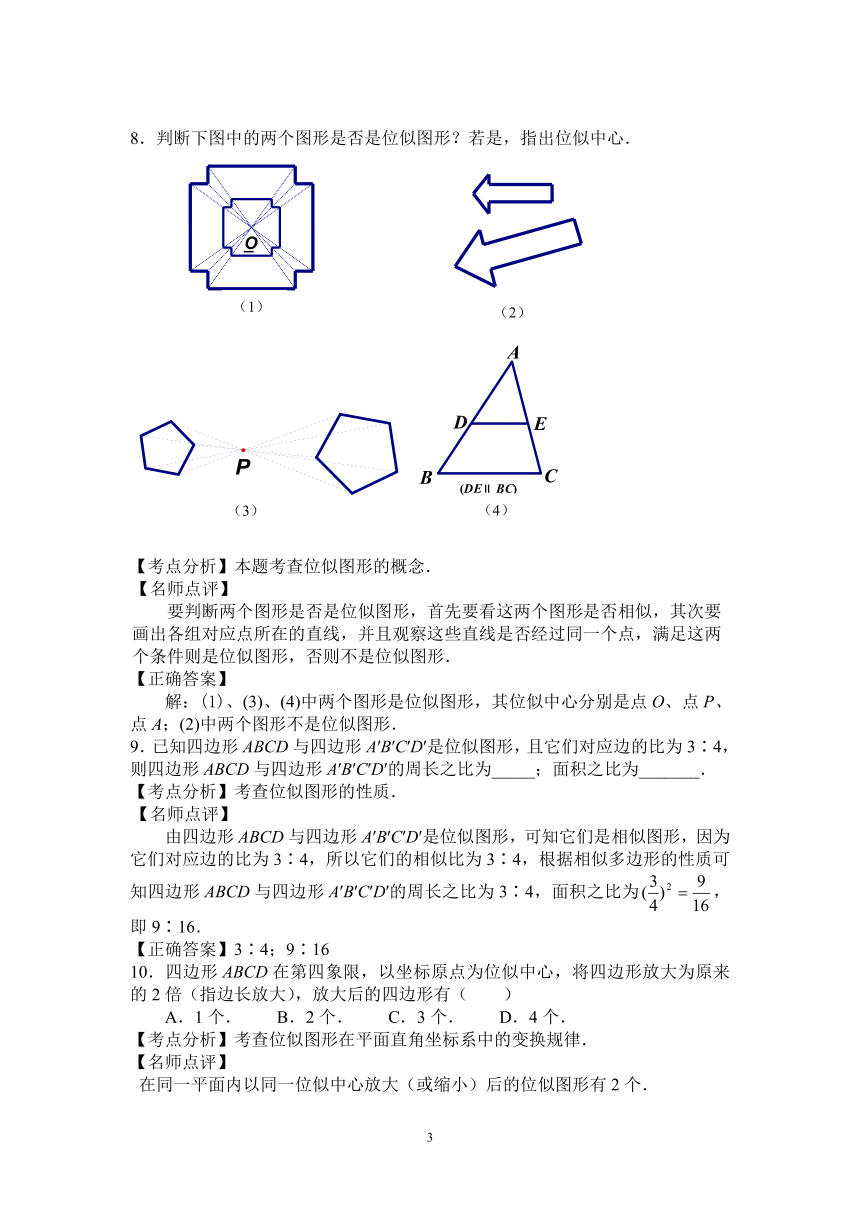
8.判断下图中的两个图形是否是位似图形?若是,指出位似中心.
【考点分析】本题考查位似图形的概念.
【名师点评】
要判断两个图形是否是位似图形,首先要看这两个图形是否相似,其次要画出各组对应点所在的直线,并且观察这些直线是否经过同一个点,满足这两个条件则是位似图形,否则不是位似图形.
【正确答案】
解:(1)、(3)、(4)中两个图形是位似图形,其位似中心分别是点O、点P、点A;(2)中两个图形不是位似图形.
9.已知四边形ABCD与四边形A′B′C′D′是位似图形,且它们对应边的比为3∶4,则四边形ABCD与四边形A′B′C′D′的周长之比为_____;面积之比为_______.
【考点分析】考查位似图形的性质.
【名师点评】
由四边形ABCD与四边形A′B′C′D′是位似图形,可知它们是相似图形,因为它们对应边的比为3∶4,所以它们的相似比为3∶4,根据相似多边形的性质可知四边形ABCD与四边形A′B′C′D′的周长之比为3∶4,面积之比为,即9∶16.
【正确答案】3∶4;9∶16
10.四边形ABCD在第四象限,以坐标原点为位似中心,将四边形放大为原来的2倍(指边长放大),放大后的四边形有( )
A.1个. B.2个. C.3个. D.4个.
【考点分析】考查位似图形在平面直角坐标系中的变换规律.
【名师点评】
在同一平面内以同一位似中心放大(或缩小)后的位似图形有2个.
【正确答案】B
〖能力提升〗
1.如图,按如下方法作图:任取一点O,连接OA、OB、OC,并取它们的中点D、E、F,连接DE、EF、DF,得到△DEF,则下列说法正确有( ).
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF周长的比为2∶1;④△ABC与△DEF面积的比为4∶1.
A.1 B.2 C.3 D.4
【考点分析】考查位似与相似的性质
【名师点评】
位似图形具有相似图形的一切性质,相似图形的周长比等于相似比,面积比等于相似比的平方.
【正确答案】D
2.在平面直角坐标系中,点A(3,4),B(-4,3),以原点O为位似中心,相似比为2,将△OAB放大为△OA′B′,则对应点A′、B′的坐标分别为_____.
【考点分析】考查位似变换的性质.
【名师点评】
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或-.
【正确答案】A′(6,8),B′(-8,6)或A′(-6,-8),B′(8,-6).
3.如图,点O是等边三角形PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形.此时,△P′Q′R′与△PQR的位似比、位似中心分别为( ).
A.2,点P B.,点P C.2,点O D.,点O
【考点分析】考查位似的相关概念.
【名师点评】
根据位似图形的定义可知,△P′Q′R′与△PQR是位似三角形.则PP′,QQ′,RR′交于点O,所以点O是位似中心,位似比为.
【正确答案】D
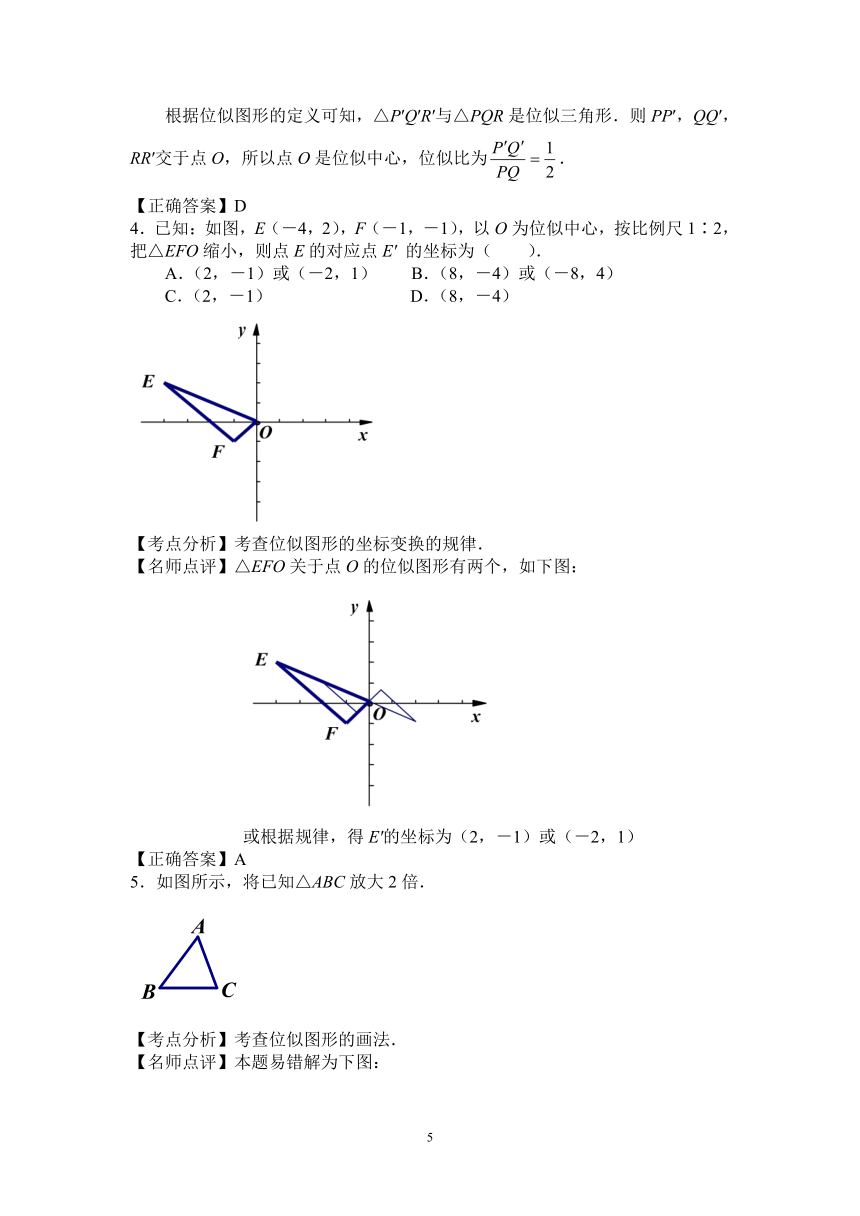
4.已知:如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1∶2,把△EFO缩小,则点E的对应点E′ 的坐标为( ).
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
【考点分析】考查位似图形的坐标变换的规律.
【名师点评】△EFO关于点O的位似图形有两个,如下图:
或根据规律,得E′的坐标为(2,-1)或(-2,1)
【正确答案】A
5.如图所示,将已知△ABC放大2倍.
【考点分析】考查位似图形的画法.
【名师点评】本题易错解为下图:
将题目要求的“放大2倍”与“放大到2倍”相混淆,“放大到2倍”意思是新图形与原图形各对应边的比为2∶1,而“放大2倍”即“放大到3倍”的意思,指新图形与原图形各对应边的比为3∶1.
【正确答案】
正确作案不唯一,选择不同的位似中心,结果也不同.如图所示,△A′B′C′即为求作的三角形.
6.如图所示,在直角坐标系中,四边形ABCD各顶点的坐标分别为
A(-1,-1),B(2,-1),C(2,2),D(-1,2),这个图形是什么图形?把各顶点的坐标都乘以2,得到的图形面积与原图形的面积有怎样的关系?再试试用不同的(≠1)值乘以各顶点的坐标,你能发现随着值的变化,图形的面积是怎样变化的?
【考点分析】考查通过计算找出规律.
【名师点评】
本题是一道规律探索题,应用以下规律:在直角坐标系内,把已知凸四边形的各顶点坐标乘以后,所得新图形与原图形是位似图形,相似比为,面积比为.
【正确答案】
如图所示,可以看出四边形ABCD是正方形,边长为3,而要求画出图形A′B′C′D′,它也是一个正方形,边长为6,可以看出,正方形A′B′C′D′的面积是原正方形ABCD面积的4倍,即倍.如果把各顶点坐标都乘以(>1),则所得图形的面积扩大为原来的倍.如果把各顶点的坐标都乘以(0<<1),则所得图形的面积缩小为原来的倍.
7.设四边形ABCD与四边形是位似图形,且位似比为,给出下列4个等式:①;②∽;③;④.其中,等式成立的个数为( )
A.1个 B.2个 C.3个 D.4个
【考点分析】考查位似多边形的性质.
【名师点评】位似多边形具有相似多边形的所有性质.
【正确答案】D
8.将一个多边形放大为原来的3倍,则放大后的图形可以作出_______个.
【考点分析】考查多边形的位似变换中心.
【名师点评】
多边形的位似变换中心可以在任何地方,通常每一个变换中心都能得到2个放大3倍的图形.
【正确答案】无数
〖拓展延伸〗
1.如图所示,在正方形ABCD的边AB,BC,CD,DA上顺次截取AA′=BB′=CC′=DD′,根据所学知识,我们可以知道四边形A′B′C′D′相似于正方形ABCD,其中点A与A′,B与B′,C与C′,D与D′为对应顶点,那么,这两个正方形是位似图形吗?如果是位似图形,请找出位似中心;如果不是位似图形,请说明理由.
【考点分析】考查位似图形的概念.
【名师点评】
两个图形是位似图形的条件是:①它们是相似图形;②两个图形的对应顶点所在直线相交于一点,即位似中心.题中的两个正方形虽是相似图形,但无论顶点间怎样的对应关系,其连线都不交于一点,因此,它们不是位似图形.
【正确答案】这两个正方形不是位似图形,因为它们的对应顶点的连线不交于同一点.
2.某出版社一位编辑在设计一本书的封面时,想把封面划分为四个矩形,其中左上角矩形与右下角矩形相似(如图),给人以和谐的感觉,那么这样的两个矩形是怎样画出来的呢?这两个矩形是位似图形吗?
【考点分析】考查利用位似图形的知识解决印刷中的版面设计的问题.
【名师点评】
在封面矩形ABCD中(如图),我们先作出一条横向分割线EF,此时要作出纵向分割线GH,使矩形AEPG与矩形PHCF相似,关键要确定两条分割线的交点P.当然,利用相似比可以算出或画出EP来.但是在设计时,两个相似矩形的大小会根据不同需要而改变,每次都计算显然很麻烦,能不能找到更好的方法呢?如果能找到P点位置的规律就更好了.现在假设两个相似的矩形已经作出来了,如图所示,连接AP,PC,则,∠AEP=
∠CFP=90°,于是△AEP∽△CFP,便有∠APE=∠CPF.这样,A,P,C三点共线,即P点必在对角线AC上,由此说明两矩形位似.
【正确答案】
解:如图所示,作对角线AC,在AC上根据需要取一点P,过P作EF∥BC,作GH∥AB,则矩形AEPG和矩形CFPH就是两个相似的矩形.因为矩形的每一个内角都是直角,又由AE∥FC,AG∥CH,可得,,则.所以矩形AEPG∽矩形CFPH,则,∠AEP=∠CFP=90°,于是△AEP∽△CFP.所以∠APE=
∠CPF.这样,A,P,C三点共线,即P点必在对角线AC上,所以矩形AEPG与矩形CFPH是位似图形.
3.在小孔成像问题中,根据如图所示,若O到AB的距离是18,O到CD的距离是6,则像CD的长是物AB长的( ).
A.3倍 B. C. D.2
【考点分析】考查位似变换的性质.
【名师点评】由题意可知△AOB∽△COD,则相似比等于对应高的比.
【正确答案】C
4.如图,为测量有障碍物相隔的A、B两点间距离,在适当处放置一水平桌面,铺上白纸,在点A、B处立上标杆,在纸上立大头针于点O,通过观测在纸上确定了点C.已知O、C、A在一条直线上,并且OA的长为OC的100倍,问接下去再怎样做,就能得出A、B两点间的距离.
【考点分析】考查添加辅助线构成位似图形,求线段的长.
【名师点评】
根据条件OA=100,因此可在纸上确定点D,使,则CD∥AB,这样△OCD和△OAB成位似图形,再量出CD的长度,通过位似比求出AB=100CD.
【正确答案】
在图上确定点D,使点D在射线OB上,并且使,则CD∥AB,CD与AB的位似比为,量出线段CD的长,再乘100,便得到A、B两点间的距离.
5.如图所示,在直角坐标系中,第一次将△OAB变换成△OAB,第二次将△OAB变换成△OAB…,已知A(1,3),A(2,4),A(4,5);B(2,0),B(4,0),B(8,0).在总结三角形的顶点坐标变化规律的基础上,按此规律推测,将△OAB进行了次变换后,顶点A,B的坐标分别是多少?
【考点分析】本题考查通过观察坐标变化寻找规律.
【名师点评】
原A(1,3)即(2,3+0),(2,4)即(2,3+1),(4,5)即(2,3+2),原B(2,0)即(2,0),B(4,0)即(2,0),B(4,0)即(2,0).
【正确答案】A(2,+3),B(2,0)
【数学花苑】
〖聪明屋〗
如图所示,在矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,
(1)说明点G是线段BC的一个三等分点;
(2)请你依照上面的画法,在原图上画出BC的一个四等分点(保留作图痕迹,不必证明).
分析:(1)因为FG⊥BC,若要说明G为BC的三等点,可转化为说明或,进而通过寻找相似三角形或根据平行线分线段成比例定理来完成解题过程.在矩形ABCD中,OE⊥BC,DC⊥BC.所以OE∥DC,所以△EFO∽△DFC.因为.所以,所以.又因为FG⊥BC,DC⊥BC,所以FG∥DC,所以△EFG∽△EDC.所以.即.所以点G是BC的一个三等点.
(2)可通过观察三等分点的画法,类似可以找到四等分点,五等分点的画法.如下图,连接DG交OC于,作⊥CE于,则即为BC的四等分点.
〖数学史话〗
七座桥的故事
沿着俄国和波兰的边界,有一条长长的布格河.这条河流经俄国的古城康尼斯堡——它就是今天俄罗斯西北边界城市加里宁格勒.
布格河横贯康尼斯堡城区,它有两条支流,一条称新河,另一条叫旧河,两河在城中心会合后,成为一条主流,叫做大河.在新旧两河与大河之间,夹着一块岛形地带,这里是城市的繁华地区.全城分为北、东、南、岛四个区,各区之间共有七座桥梁联系着.
人们长期生活在河畔、岛上,来往于七桥之间.有人提出这样一个问题:能不能一次走遍所有的七座桥,而每座桥只准经过一次?问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决.最后,人们只好把这个问题向俄国科学院院士欧拉提出,请他帮助解决.
公元1737年,欧拉接到了“七桥问题”,当时他三十岁.他心里想:先试试看吧.他从中间的岛区出发,经过一号桥到达北区,又从二号桥回到岛区,过四号桥进入东区,再经五号桥到达南区,然后过六号桥回到岛区.现在,只剩下三号和七号两座桥没有通过了.显然,从岛区要过三号桥,只有先过一号、二号或四号桥,但这三座桥都走过了.这种走法宣告失败.欧拉又换了一种走法:
岛东北岛南岛北
这种走法还是不行,因为五号桥还没有走过.
欧拉连试了好几种走法都不行,这问题可真不简单!他算了一下,走法很多,共有
7×6×5×4×3×2×1=5040(种).
好家伙,这样一种方法,一种方法试下去,要试到哪一天,才能得出答案呢?他想:不能这样呆笨地试下去,得想别的方法.
聪明的欧拉终于想出一个巧妙的办法.他用A代表岛区、B、C、D分别代表北、东、西三区,并用曲线弧或直线段表示七座桥,这样一来,七座桥的问题,就转变为数学分支“图论”中的一个一笔画问题,即:能不能一笔头不重复地画出右边的这个图形.
欧拉集中精力研究了这个图形,发现中间每经过一点,总有画到那一点的一条线和从那一点画出来的一条线.这就是说,除起点和终点以外,经过中间各点的线必然是偶数.像上面这个图,因为是一个封闭的曲线,因此,经过所有点的线都必须是偶数才行.而这个图中,经过A点的线有五条,经过B、C、D三点的线都是三条,没有一个是偶数,从而说明,无论从那一点出发,最后总有一条线没有画到,也就是有一座桥没有走到.欧拉终于证明了,要想一次不重复地走完七座桥,那是不可能的.
天才的欧拉只用了一步证明,就概括了5040种不同的走法,从这里我们可以看到,数学的威力多么大呀!
〖生活中的数学〗
射击比赛用的那枪靶,它的图形是由10个同心圆组成,由内向外把圆编为1,2,3,……10环,每环的面积相等,意思就是第二个圆与第一个圆的面积之差等于第3个圆与第二个圆的面积之差,依次类推,求这10个圆的半径之比.
这是一道相似圆形的相关问题.
解题过程:设第一个圆的面积为=π,半径为.
所以第二个圆的面积为=2π,半径为,依次类推=10π.
所以∶=π∶π=∶=π∶2π=1∶2
所以∶=1∶
同理可得:∶∶∶…=1∶∶∶…
此题得解.
反思此题,若将这题中的圆改为正方形,正五边形、正六边形……甚至正n边形,更甚至是普通多边形,那么又会怎么样呢?
再反回去看看关于相似三角形的相关性质.
若两个三角形相似,则那两个三角形的面积之比等于相似比的平方.
那是不是在平面中相似的图形都有相似三角形的这一性质呢?
(1)求证:同心正方形的面积之比等于相似比的平方.
仍设最里面那个正方形的面积为,边长为.
所以第二个正方形的面积为,边长为.
∶=∶
相似此等于对应边之比
可得面积之比为对应边之比的平方.
(2)再求证:同心正五边形的面积之比等于相似比的平方.
仍设最里面那个正边形的面积为,边长为,依此类推.
如图所示:
正五边形ABCDE为第一个,面积为,O为其中心.正五边形A′B′C′D′E′为第二个,面积为,O为其中心.
因为是同心正五边形,所以 A,A′,O三点共线,B,B′,O也共线.
第二个正五边形的顶点分别在OA、OB、OC、OD、OE的延长线上.
由正五边形的五边相等,所以 ,
易知 ,
所以
同理得
所以
可证得,相似五边形的面积之比为相似比的平方.正三角形、正方形、正五边形都满足相似图形的面积之比为相似比的平方,那是不是正n边形都满足呢?
如图,设O为这些相似正n边形的中心,为最里面的那个正n边形的一条边,其长度为,设,
所以 最里面那个正n边形的面积.
为第二个正n边形的一条边与相对应,其长度为.
因为 第一个正n边形相似于第二个正n边形.
所以∥, 所以 △OA1A2∽△
所以 , 所以
所以, 所以
可证得:相似正n边形的面积之比等于相似比的平方.
于此可得,相似的正多边形的面积之比等于相似比平方.
那对于普通的多边形呢?会不会仍然满足上述规律?
对于任何一个多边形,其内一定存在一点O,使点O与其每个顶点的连线将该多边形分成与其边数相同的三角形,且这些三角形面积相等.
所以对于任意一个n边形,如图:
AB为最里面的那个n边形的一条边,O为其中心,所以第二个n边形的对应顶点在OA、OB的延长线上,设为第二个n边形的对应边,因而n边形也与之相似.所以 AB//,设AB=,.
所以,
所以第一个n边形和第二个n边形的面积比为:
同理可证得,相似多边形的面积比为相似比的平方.
而对于那些曲线图形,我们可将其看作很多很短的线段相连而成,这样就将曲线图形转化为多边形的情况,同样满足上述条件.
综上所述,任何相似的图形的面积之比等于相似比的平方.
若某广告公司要在一高墙上做广告牌,就需知道那部分墙的面积有多大,才能确定广告牌的面积大小,若直接去测量或用各种测量仪对其进行测量,不但麻烦甚至有危险.
若利用上述规律,我们只需对其拍照,再把照片上该区域的面积求出来,再根照相机的相关数据可求出相似比,根据上述规律可轻松,方便地算出实际面积大小.
再比如要装修公司进行装修之前都要对材料进行估算.要正确估算就得知道要装修的面积,若运用同样的方法,比土办法就更显方便、准确、快捷.
诸如此类的问题,运用上面的规律,用一些简单的工具就可完成复杂的操作,何乐而不为?
(2)
(1)
(4)
(3)
A’
A
E’
D’
C’
B’
E
D
C
B
_
O
O
O
PAGE
16
〖基础训练〗
1.位似图形上某一对对应点到位似中心的距离分别是10cm和5cm,则他们的位似比是___________.
【考点分析】考查位似比的概念.
【名师点评】位似比即位似图形的相似比,亦为对应点到位似中心的距离比.
【正确答案】2
2.下列判断中,正确的是( )
A.相似图形一定是位似图形.
B.位似图形一定是相似图形.
C.全等的图形一定是位似图形.
D.位似图形一定是全等图形.
【考点分析】考查相似图形、位似图形、全等图形之间的关系.
【名师点评】
位似图形是相似图形的一种特殊情况,所以位似图形肯定是相似图形,而相似图形不一定是位似图形;全等又是相似的特殊情况,与位似没有直接联系,全等的图形不一定是位似图形,位似图形也不一定是全等图形.
【正确答案】 B
3.若两个图形位似,则下列叙述不正确的是( )
A.每对对应点所在的直线相交于同一点.
B.两个图形上的对应线段之比等于位似比.
C.两个图形上的对应线段必平行.
D.两个图形的面积之比等于位似比的平方.
【考点分析】考查两个位似图形之间的关系.
【名师点评】
由位似图形的定义可知,两个图形位似必须符合三个条件:①相似,②对应边平行或在同一直线上,③对应顶点的连线交与一点.对应线段有可能在同一直线上,所以选项C错误.
【正确答案】C
4.用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
A.只能选在原图形的外部.
B.只能选在原图形的内部.
C.只能选在原图形的边上.
D.可以选择任意位置.
【考点分析】考查位似中心的概念.
【名师点评】位似图形的位似中心可以选择平面内的任意位置.
【正确答案】D
5.△OCD与△OAB是位似图形,其中位似比为2∶3,若将两个图形放大,使放大前后对应线段的比为1∶2,则放大后两个三角形的位似比为( ).
A.4∶3 B.1∶3 C.2∶3 D.1∶2
【考点分析】考查位似比与相似比的关系.
【名师点评】
位似比即位似图形的相似比,亦为对应点到位似中心的距离比,相似比为相似图形对应边的比,△OCD与△OAB都放大2倍后相似比不变.
【正确答案】C
6.在如图所示的四个图案中的两个图形可以看作是位似变换得到的是( ).
A.(1)(2) B.(1)(3) C.(3)(4) D.(1)(4)
【考点分析】考查位似图形的判断.
【名师点评】
位似图形的判断要根据定义,须符合三个条件:①相似,②对应边平行或在同一直线上,③对应顶点的连线交与一点.
【正确答案】D
7.平面直角坐标系中,有一条鱼,它有六个顶点,下列说法中正确的是( )
A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似.
B.将各点纵坐标乘以2, 横坐标不变,得到的鱼与原来的鱼位似.
C.将各点横、纵坐标都乘以2,得到的鱼与原来的鱼位似.
D.将各点横坐标乘以2,纵坐标乘以,得到的鱼与原来的鱼位似.
【考点分析】考查以原点为位似中心,两位似图形坐标之间的关系.
【名师点评】
平面直角坐标系中,以原点为位似中心,两位似图形横、纵坐标之比都为或-.
【正确答案】C
8.判断下图中的两个图形是否是位似图形?若是,指出位似中心.
【考点分析】本题考查位似图形的概念.
【名师点评】
要判断两个图形是否是位似图形,首先要看这两个图形是否相似,其次要画出各组对应点所在的直线,并且观察这些直线是否经过同一个点,满足这两个条件则是位似图形,否则不是位似图形.
【正确答案】
解:(1)、(3)、(4)中两个图形是位似图形,其位似中心分别是点O、点P、点A;(2)中两个图形不是位似图形.
9.已知四边形ABCD与四边形A′B′C′D′是位似图形,且它们对应边的比为3∶4,则四边形ABCD与四边形A′B′C′D′的周长之比为_____;面积之比为_______.
【考点分析】考查位似图形的性质.
【名师点评】
由四边形ABCD与四边形A′B′C′D′是位似图形,可知它们是相似图形,因为它们对应边的比为3∶4,所以它们的相似比为3∶4,根据相似多边形的性质可知四边形ABCD与四边形A′B′C′D′的周长之比为3∶4,面积之比为,即9∶16.
【正确答案】3∶4;9∶16
10.四边形ABCD在第四象限,以坐标原点为位似中心,将四边形放大为原来的2倍(指边长放大),放大后的四边形有( )
A.1个. B.2个. C.3个. D.4个.
【考点分析】考查位似图形在平面直角坐标系中的变换规律.
【名师点评】
在同一平面内以同一位似中心放大(或缩小)后的位似图形有2个.
【正确答案】B
〖能力提升〗
1.如图,按如下方法作图:任取一点O,连接OA、OB、OC,并取它们的中点D、E、F,连接DE、EF、DF,得到△DEF,则下列说法正确有( ).
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF周长的比为2∶1;④△ABC与△DEF面积的比为4∶1.
A.1 B.2 C.3 D.4
【考点分析】考查位似与相似的性质
【名师点评】
位似图形具有相似图形的一切性质,相似图形的周长比等于相似比,面积比等于相似比的平方.
【正确答案】D
2.在平面直角坐标系中,点A(3,4),B(-4,3),以原点O为位似中心,相似比为2,将△OAB放大为△OA′B′,则对应点A′、B′的坐标分别为_____.
【考点分析】考查位似变换的性质.
【名师点评】
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或-.
【正确答案】A′(6,8),B′(-8,6)或A′(-6,-8),B′(8,-6).
3.如图,点O是等边三角形PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形.此时,△P′Q′R′与△PQR的位似比、位似中心分别为( ).
A.2,点P B.,点P C.2,点O D.,点O
【考点分析】考查位似的相关概念.
【名师点评】
根据位似图形的定义可知,△P′Q′R′与△PQR是位似三角形.则PP′,QQ′,RR′交于点O,所以点O是位似中心,位似比为.
【正确答案】D
4.已知:如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1∶2,把△EFO缩小,则点E的对应点E′ 的坐标为( ).
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
【考点分析】考查位似图形的坐标变换的规律.
【名师点评】△EFO关于点O的位似图形有两个,如下图:
或根据规律,得E′的坐标为(2,-1)或(-2,1)
【正确答案】A
5.如图所示,将已知△ABC放大2倍.
【考点分析】考查位似图形的画法.
【名师点评】本题易错解为下图:
将题目要求的“放大2倍”与“放大到2倍”相混淆,“放大到2倍”意思是新图形与原图形各对应边的比为2∶1,而“放大2倍”即“放大到3倍”的意思,指新图形与原图形各对应边的比为3∶1.
【正确答案】
正确作案不唯一,选择不同的位似中心,结果也不同.如图所示,△A′B′C′即为求作的三角形.
6.如图所示,在直角坐标系中,四边形ABCD各顶点的坐标分别为
A(-1,-1),B(2,-1),C(2,2),D(-1,2),这个图形是什么图形?把各顶点的坐标都乘以2,得到的图形面积与原图形的面积有怎样的关系?再试试用不同的(≠1)值乘以各顶点的坐标,你能发现随着值的变化,图形的面积是怎样变化的?
【考点分析】考查通过计算找出规律.
【名师点评】
本题是一道规律探索题,应用以下规律:在直角坐标系内,把已知凸四边形的各顶点坐标乘以后,所得新图形与原图形是位似图形,相似比为,面积比为.
【正确答案】
如图所示,可以看出四边形ABCD是正方形,边长为3,而要求画出图形A′B′C′D′,它也是一个正方形,边长为6,可以看出,正方形A′B′C′D′的面积是原正方形ABCD面积的4倍,即倍.如果把各顶点坐标都乘以(>1),则所得图形的面积扩大为原来的倍.如果把各顶点的坐标都乘以(0<<1),则所得图形的面积缩小为原来的倍.
7.设四边形ABCD与四边形是位似图形,且位似比为,给出下列4个等式:①;②∽;③;④.其中,等式成立的个数为( )
A.1个 B.2个 C.3个 D.4个
【考点分析】考查位似多边形的性质.
【名师点评】位似多边形具有相似多边形的所有性质.
【正确答案】D
8.将一个多边形放大为原来的3倍,则放大后的图形可以作出_______个.
【考点分析】考查多边形的位似变换中心.
【名师点评】
多边形的位似变换中心可以在任何地方,通常每一个变换中心都能得到2个放大3倍的图形.
【正确答案】无数
〖拓展延伸〗
1.如图所示,在正方形ABCD的边AB,BC,CD,DA上顺次截取AA′=BB′=CC′=DD′,根据所学知识,我们可以知道四边形A′B′C′D′相似于正方形ABCD,其中点A与A′,B与B′,C与C′,D与D′为对应顶点,那么,这两个正方形是位似图形吗?如果是位似图形,请找出位似中心;如果不是位似图形,请说明理由.
【考点分析】考查位似图形的概念.
【名师点评】
两个图形是位似图形的条件是:①它们是相似图形;②两个图形的对应顶点所在直线相交于一点,即位似中心.题中的两个正方形虽是相似图形,但无论顶点间怎样的对应关系,其连线都不交于一点,因此,它们不是位似图形.
【正确答案】这两个正方形不是位似图形,因为它们的对应顶点的连线不交于同一点.
2.某出版社一位编辑在设计一本书的封面时,想把封面划分为四个矩形,其中左上角矩形与右下角矩形相似(如图),给人以和谐的感觉,那么这样的两个矩形是怎样画出来的呢?这两个矩形是位似图形吗?
【考点分析】考查利用位似图形的知识解决印刷中的版面设计的问题.
【名师点评】
在封面矩形ABCD中(如图),我们先作出一条横向分割线EF,此时要作出纵向分割线GH,使矩形AEPG与矩形PHCF相似,关键要确定两条分割线的交点P.当然,利用相似比可以算出或画出EP来.但是在设计时,两个相似矩形的大小会根据不同需要而改变,每次都计算显然很麻烦,能不能找到更好的方法呢?如果能找到P点位置的规律就更好了.现在假设两个相似的矩形已经作出来了,如图所示,连接AP,PC,则,∠AEP=
∠CFP=90°,于是△AEP∽△CFP,便有∠APE=∠CPF.这样,A,P,C三点共线,即P点必在对角线AC上,由此说明两矩形位似.
【正确答案】
解:如图所示,作对角线AC,在AC上根据需要取一点P,过P作EF∥BC,作GH∥AB,则矩形AEPG和矩形CFPH就是两个相似的矩形.因为矩形的每一个内角都是直角,又由AE∥FC,AG∥CH,可得,,则.所以矩形AEPG∽矩形CFPH,则,∠AEP=∠CFP=90°,于是△AEP∽△CFP.所以∠APE=
∠CPF.这样,A,P,C三点共线,即P点必在对角线AC上,所以矩形AEPG与矩形CFPH是位似图形.
3.在小孔成像问题中,根据如图所示,若O到AB的距离是18,O到CD的距离是6,则像CD的长是物AB长的( ).
A.3倍 B. C. D.2
【考点分析】考查位似变换的性质.
【名师点评】由题意可知△AOB∽△COD,则相似比等于对应高的比.
【正确答案】C
4.如图,为测量有障碍物相隔的A、B两点间距离,在适当处放置一水平桌面,铺上白纸,在点A、B处立上标杆,在纸上立大头针于点O,通过观测在纸上确定了点C.已知O、C、A在一条直线上,并且OA的长为OC的100倍,问接下去再怎样做,就能得出A、B两点间的距离.
【考点分析】考查添加辅助线构成位似图形,求线段的长.
【名师点评】
根据条件OA=100,因此可在纸上确定点D,使,则CD∥AB,这样△OCD和△OAB成位似图形,再量出CD的长度,通过位似比求出AB=100CD.
【正确答案】
在图上确定点D,使点D在射线OB上,并且使,则CD∥AB,CD与AB的位似比为,量出线段CD的长,再乘100,便得到A、B两点间的距离.
5.如图所示,在直角坐标系中,第一次将△OAB变换成△OAB,第二次将△OAB变换成△OAB…,已知A(1,3),A(2,4),A(4,5);B(2,0),B(4,0),B(8,0).在总结三角形的顶点坐标变化规律的基础上,按此规律推测,将△OAB进行了次变换后,顶点A,B的坐标分别是多少?
【考点分析】本题考查通过观察坐标变化寻找规律.
【名师点评】
原A(1,3)即(2,3+0),(2,4)即(2,3+1),(4,5)即(2,3+2),原B(2,0)即(2,0),B(4,0)即(2,0),B(4,0)即(2,0).
【正确答案】A(2,+3),B(2,0)
【数学花苑】
〖聪明屋〗
如图所示,在矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,
(1)说明点G是线段BC的一个三等分点;
(2)请你依照上面的画法,在原图上画出BC的一个四等分点(保留作图痕迹,不必证明).
分析:(1)因为FG⊥BC,若要说明G为BC的三等点,可转化为说明或,进而通过寻找相似三角形或根据平行线分线段成比例定理来完成解题过程.在矩形ABCD中,OE⊥BC,DC⊥BC.所以OE∥DC,所以△EFO∽△DFC.因为.所以,所以.又因为FG⊥BC,DC⊥BC,所以FG∥DC,所以△EFG∽△EDC.所以.即.所以点G是BC的一个三等点.
(2)可通过观察三等分点的画法,类似可以找到四等分点,五等分点的画法.如下图,连接DG交OC于,作⊥CE于,则即为BC的四等分点.
〖数学史话〗
七座桥的故事
沿着俄国和波兰的边界,有一条长长的布格河.这条河流经俄国的古城康尼斯堡——它就是今天俄罗斯西北边界城市加里宁格勒.
布格河横贯康尼斯堡城区,它有两条支流,一条称新河,另一条叫旧河,两河在城中心会合后,成为一条主流,叫做大河.在新旧两河与大河之间,夹着一块岛形地带,这里是城市的繁华地区.全城分为北、东、南、岛四个区,各区之间共有七座桥梁联系着.
人们长期生活在河畔、岛上,来往于七桥之间.有人提出这样一个问题:能不能一次走遍所有的七座桥,而每座桥只准经过一次?问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决.最后,人们只好把这个问题向俄国科学院院士欧拉提出,请他帮助解决.
公元1737年,欧拉接到了“七桥问题”,当时他三十岁.他心里想:先试试看吧.他从中间的岛区出发,经过一号桥到达北区,又从二号桥回到岛区,过四号桥进入东区,再经五号桥到达南区,然后过六号桥回到岛区.现在,只剩下三号和七号两座桥没有通过了.显然,从岛区要过三号桥,只有先过一号、二号或四号桥,但这三座桥都走过了.这种走法宣告失败.欧拉又换了一种走法:
岛东北岛南岛北
这种走法还是不行,因为五号桥还没有走过.
欧拉连试了好几种走法都不行,这问题可真不简单!他算了一下,走法很多,共有
7×6×5×4×3×2×1=5040(种).
好家伙,这样一种方法,一种方法试下去,要试到哪一天,才能得出答案呢?他想:不能这样呆笨地试下去,得想别的方法.
聪明的欧拉终于想出一个巧妙的办法.他用A代表岛区、B、C、D分别代表北、东、西三区,并用曲线弧或直线段表示七座桥,这样一来,七座桥的问题,就转变为数学分支“图论”中的一个一笔画问题,即:能不能一笔头不重复地画出右边的这个图形.
欧拉集中精力研究了这个图形,发现中间每经过一点,总有画到那一点的一条线和从那一点画出来的一条线.这就是说,除起点和终点以外,经过中间各点的线必然是偶数.像上面这个图,因为是一个封闭的曲线,因此,经过所有点的线都必须是偶数才行.而这个图中,经过A点的线有五条,经过B、C、D三点的线都是三条,没有一个是偶数,从而说明,无论从那一点出发,最后总有一条线没有画到,也就是有一座桥没有走到.欧拉终于证明了,要想一次不重复地走完七座桥,那是不可能的.
天才的欧拉只用了一步证明,就概括了5040种不同的走法,从这里我们可以看到,数学的威力多么大呀!
〖生活中的数学〗
射击比赛用的那枪靶,它的图形是由10个同心圆组成,由内向外把圆编为1,2,3,……10环,每环的面积相等,意思就是第二个圆与第一个圆的面积之差等于第3个圆与第二个圆的面积之差,依次类推,求这10个圆的半径之比.
这是一道相似圆形的相关问题.
解题过程:设第一个圆的面积为=π,半径为.
所以第二个圆的面积为=2π,半径为,依次类推=10π.
所以∶=π∶π=∶=π∶2π=1∶2
所以∶=1∶
同理可得:∶∶∶…=1∶∶∶…
此题得解.
反思此题,若将这题中的圆改为正方形,正五边形、正六边形……甚至正n边形,更甚至是普通多边形,那么又会怎么样呢?
再反回去看看关于相似三角形的相关性质.
若两个三角形相似,则那两个三角形的面积之比等于相似比的平方.
那是不是在平面中相似的图形都有相似三角形的这一性质呢?
(1)求证:同心正方形的面积之比等于相似比的平方.
仍设最里面那个正方形的面积为,边长为.
所以第二个正方形的面积为,边长为.
∶=∶
相似此等于对应边之比
可得面积之比为对应边之比的平方.
(2)再求证:同心正五边形的面积之比等于相似比的平方.
仍设最里面那个正边形的面积为,边长为,依此类推.
如图所示:
正五边形ABCDE为第一个,面积为,O为其中心.正五边形A′B′C′D′E′为第二个,面积为,O为其中心.
因为是同心正五边形,所以 A,A′,O三点共线,B,B′,O也共线.
第二个正五边形的顶点分别在OA、OB、OC、OD、OE的延长线上.
由正五边形的五边相等,所以 ,
易知 ,
所以
同理得
所以
可证得,相似五边形的面积之比为相似比的平方.正三角形、正方形、正五边形都满足相似图形的面积之比为相似比的平方,那是不是正n边形都满足呢?
如图,设O为这些相似正n边形的中心,为最里面的那个正n边形的一条边,其长度为,设,
所以 最里面那个正n边形的面积.
为第二个正n边形的一条边与相对应,其长度为.
因为 第一个正n边形相似于第二个正n边形.
所以∥, 所以 △OA1A2∽△
所以 , 所以
所以, 所以
可证得:相似正n边形的面积之比等于相似比的平方.
于此可得,相似的正多边形的面积之比等于相似比平方.
那对于普通的多边形呢?会不会仍然满足上述规律?
对于任何一个多边形,其内一定存在一点O,使点O与其每个顶点的连线将该多边形分成与其边数相同的三角形,且这些三角形面积相等.
所以对于任意一个n边形,如图:
AB为最里面的那个n边形的一条边,O为其中心,所以第二个n边形的对应顶点在OA、OB的延长线上,设为第二个n边形的对应边,因而n边形也与之相似.所以 AB//,设AB=,.
所以,
所以第一个n边形和第二个n边形的面积比为:
同理可证得,相似多边形的面积比为相似比的平方.
而对于那些曲线图形,我们可将其看作很多很短的线段相连而成,这样就将曲线图形转化为多边形的情况,同样满足上述条件.
综上所述,任何相似的图形的面积之比等于相似比的平方.
若某广告公司要在一高墙上做广告牌,就需知道那部分墙的面积有多大,才能确定广告牌的面积大小,若直接去测量或用各种测量仪对其进行测量,不但麻烦甚至有危险.
若利用上述规律,我们只需对其拍照,再把照片上该区域的面积求出来,再根照相机的相关数据可求出相似比,根据上述规律可轻松,方便地算出实际面积大小.
再比如要装修公司进行装修之前都要对材料进行估算.要正确估算就得知道要装修的面积,若运用同样的方法,比土办法就更显方便、准确、快捷.
诸如此类的问题,运用上面的规律,用一些简单的工具就可完成复杂的操作,何乐而不为?
(2)
(1)
(4)
(3)
A’
A
E’
D’
C’
B’
E
D
C
B
_
O
O
O
PAGE
16
