5.5.1两角差的余弦公式 第一课时 课件(共35张PPT)
文档属性
| 名称 | 5.5.1两角差的余弦公式 第一课时 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 08:33:46 | ||
图片预览











文档简介
(共35张PPT)
5.5 三角恒等变换
第五章 三角函数
5.5.1 两角和与差的正弦、余弦和正切公式
第一课时 两角差的余弦公式
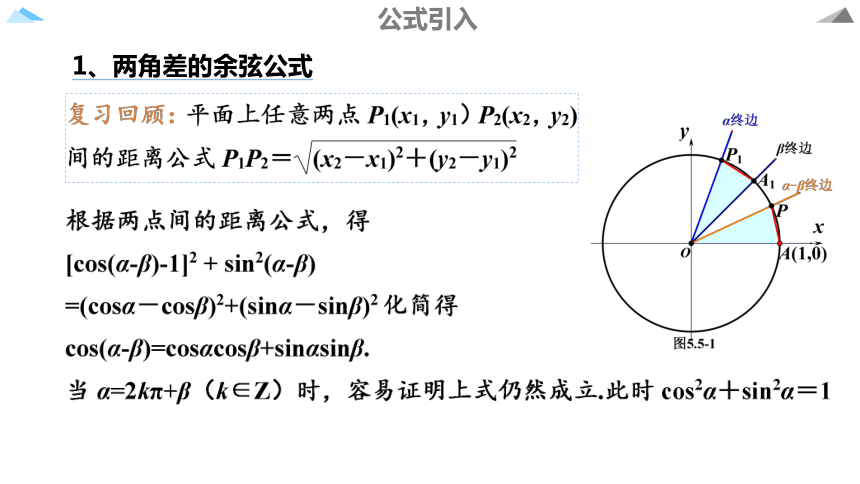
1、两角差的余弦公式
公式引入
1、两角差的余弦公式
公式引入
1、两角差的余弦公式
公式引入
1、两角差的余弦公式
公式理解
1、两角差的余弦公式
巩固与练习
巩固与练习
注意:非特殊角的三角函数求值,要充分考虑能否转化为两特殊角的和与差
巩固与练习
注意:考察7°与15°、8°内在联系,不难发现
7°=15°-8°
巩固与练习
规律方法
巩固与练习
巩固与练习
巩固与练习
注意到:
=( + )-
巩固与练习
巩固与练习
规律方法
公式引入(1)
我们注意到
α+β与α-β之间的联系α+β=α-(-β),
则由公式C(α-β),有 cos(α+β)= cos[α-(-β)]
=cosαcos(-β)+sinαsin(-β)
=cosαcosβ-sinαsinβ.
于是得到了两角和的余弦公式,简记作C(α+β).
cos(α+β)= cosαcosβ-sinαsinβ. ( C(α+β) )
这里用到的是加法和减法的联系,也可用换元的观点来考虑:由于公式C(α-β)对于任意α,β都成立,那么把其中的β换成-β后,也一定成立,由此也可推得公式C(α+β)
公式理解(1)
cos(α-β)= cosαcosβ+sinαsinβ. ( C(α-β) )
cos(α+β)= cosαcosβ-sinαsinβ. ( C(α+β) )
观察余弦和与差的公式特点
两角和与差的余弦公式的记忆为:“余余正正,符号相异”.
①“余余正正”表示展开后的两项分别为两角的余弦乘余弦,正弦乘正弦,
②“符号相异”表示展开后两项之间的连接符号与展开前两角之间的连接符号相异.
公式引入(2)
比较cos(α+β)、cos(α-β)与sin( - )、sin( + )它们的异同点是什么?
它们包含的角相同,只是三角函数种类名称式不同.
问题2
你能根据两角和与差的余弦公式推导出用任意角 ,β的正弦、余弦表示的sin( - )及sin( + )公式吗?
追问2:它们之间有何种联系呢?你想做怎样的转化?
公式引入(2)
sin(- )=cos
cos(- )=sin
sin(+ )= cos
cos(+ )= -sin
诱导公式五、六是什么呢?
公式引入(2)
推导 - 的正弦公式:
记忆口诀:
“正余余正,符号相同”
公式引入(3)
公式引入(3)
公式理解(2)
巩固与练习
巩固与练习
巩固与练习
巩固与练习
分析:和、差角公式把α±β的三角函数式转化成了α,β的三角函数式,如果反过来,从右到左使用公式,就可以将上述三角函数式化简,
要熟记展开公式的结构特点,以便做到公式的反向应用
巩固与练习
(3)首先观察分式特点
一是貌似和角的正切公式;
二是 1=tan45°
同学们思考, (3)还有其他解法吗?
巩固与练习
巩固与练习
巩固与练习
巩固与练习
规律方法
深化与思考
×
×
√
×
小结
限时小练
简解答:
5.5 三角恒等变换
第五章 三角函数
5.5.1 两角和与差的正弦、余弦和正切公式
第一课时 两角差的余弦公式
1、两角差的余弦公式
公式引入
1、两角差的余弦公式
公式引入
1、两角差的余弦公式
公式引入
1、两角差的余弦公式
公式理解
1、两角差的余弦公式
巩固与练习
巩固与练习
注意:非特殊角的三角函数求值,要充分考虑能否转化为两特殊角的和与差
巩固与练习
注意:考察7°与15°、8°内在联系,不难发现
7°=15°-8°
巩固与练习
规律方法
巩固与练习
巩固与练习
巩固与练习
注意到:
=( + )-
巩固与练习
巩固与练习
规律方法
公式引入(1)
我们注意到
α+β与α-β之间的联系α+β=α-(-β),
则由公式C(α-β),有 cos(α+β)= cos[α-(-β)]
=cosαcos(-β)+sinαsin(-β)
=cosαcosβ-sinαsinβ.
于是得到了两角和的余弦公式,简记作C(α+β).
cos(α+β)= cosαcosβ-sinαsinβ. ( C(α+β) )
这里用到的是加法和减法的联系,也可用换元的观点来考虑:由于公式C(α-β)对于任意α,β都成立,那么把其中的β换成-β后,也一定成立,由此也可推得公式C(α+β)
公式理解(1)
cos(α-β)= cosαcosβ+sinαsinβ. ( C(α-β) )
cos(α+β)= cosαcosβ-sinαsinβ. ( C(α+β) )
观察余弦和与差的公式特点
两角和与差的余弦公式的记忆为:“余余正正,符号相异”.
①“余余正正”表示展开后的两项分别为两角的余弦乘余弦,正弦乘正弦,
②“符号相异”表示展开后两项之间的连接符号与展开前两角之间的连接符号相异.
公式引入(2)
比较cos(α+β)、cos(α-β)与sin( - )、sin( + )它们的异同点是什么?
它们包含的角相同,只是三角函数种类名称式不同.
问题2
你能根据两角和与差的余弦公式推导出用任意角 ,β的正弦、余弦表示的sin( - )及sin( + )公式吗?
追问2:它们之间有何种联系呢?你想做怎样的转化?
公式引入(2)
sin(- )=cos
cos(- )=sin
sin(+ )= cos
cos(+ )= -sin
诱导公式五、六是什么呢?
公式引入(2)
推导 - 的正弦公式:
记忆口诀:
“正余余正,符号相同”
公式引入(3)
公式引入(3)
公式理解(2)
巩固与练习
巩固与练习
巩固与练习
巩固与练习
分析:和、差角公式把α±β的三角函数式转化成了α,β的三角函数式,如果反过来,从右到左使用公式,就可以将上述三角函数式化简,
要熟记展开公式的结构特点,以便做到公式的反向应用
巩固与练习
(3)首先观察分式特点
一是貌似和角的正切公式;
二是 1=tan45°
同学们思考, (3)还有其他解法吗?
巩固与练习
巩固与练习
巩固与练习
巩固与练习
规律方法
深化与思考
×
×
√
×
小结
限时小练
简解答:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
