4.2 简单随机抽样调查 课件(共15张PPT) 青岛版数学七年级上册
文档属性
| 名称 | 4.2 简单随机抽样调查 课件(共15张PPT) 青岛版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 10:14:31 | ||
图片预览





文档简介
(共15张PPT)
4.2 简单随机抽样调查
第4章 数据的收集、整理与描述
1.知道抽样调查的优缺点,能判断抽取的样本是否具有代表性.
典型例题
当堂检测
学习目标
课堂总结
2.会设计恰当的抽样调查方案.
议一议:抽样调查的优点是什么?
典型例题
当堂检测
学习目标
课堂总结
抽样调查有缺点吗?应该注意些什么?
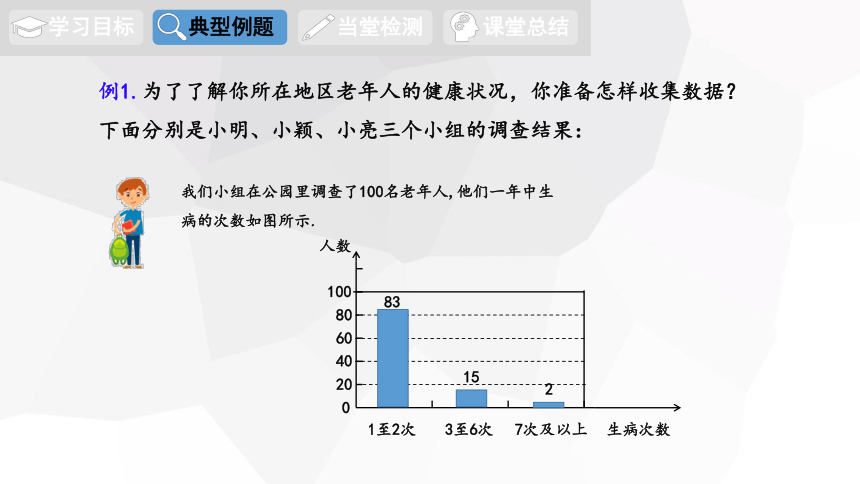
例1.为了了解你所在地区老年人的健康状况,你准备怎样收集数据?
下面分别是小明、小颖、小亮三个小组的调查结果:
我们小组在公园里调查了100名老年人,他们一年中生病的次数如图所示.
80
20
0
60
100
40
1至2次
3至6次
7次及以上
83
15
2
人数
生病次数
典型例题
当堂检测
学习目标
课堂总结
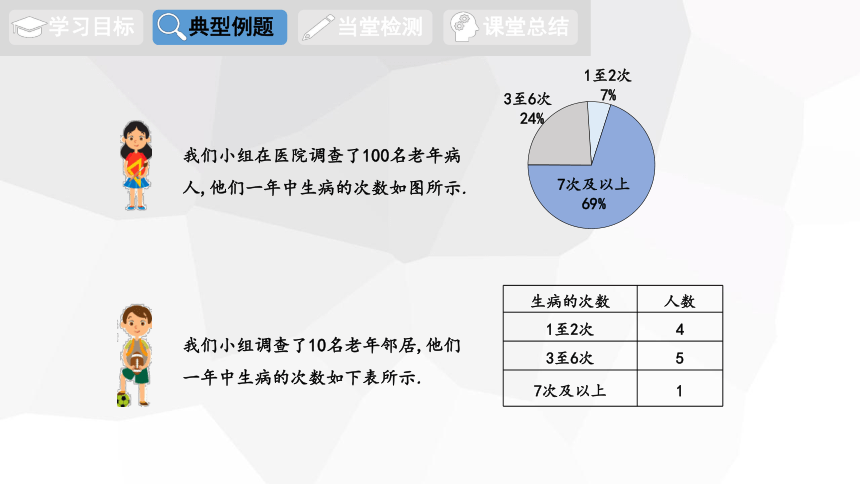
我们小组在医院调查了100名老年病人,他们一年中生病的次数如图所示.
我们小组调查了10名老年邻居,他们一年中生病的次数如下表所示.
生病的次数
人数
1至2次
4
3至6次
5
7次及以上
1
1至2次
7%
3至6次
24%
7次及以上
69%
典型例题
当堂检测
学习目标
课堂总结
(1)你同意他们的做法吗 说说你的理由.
小明调查的对象是选自公园里的老年人.常去公园里活动
的老年人,平时一定注意身体的保健,一定注意修身、养性、加强体育锻炼,所以身体较健康.
另一方面,公园建在城市里,相对于农村中的老年人去公园的较少.这100人中不同文化程度、不同职业、城市和乡村等不同层次的老人是否都有所选取,选取人数的比例是否合理,是否具有代表性与广泛性都是我们在收集数据中需要考虑的.
所以,小明收集的数据缺乏代表性和广泛性.
典型例题
当堂检测
学习目标
课堂总结
小颖收集的数据来自医院看病的100名老年人,这部分人相对体质较弱.我认为用这些数据得到的调查结果不准确,因为收集的数据缺乏代表性和广泛性.
小亮仅仅调查了10位老年人.因为样本太小了,所以不能据此推断某地区老年人的健康状况.
典型例题
当堂检测
学习目标
课堂总结
(2)为了了解该地区老年人的健康状况,你认为应当怎样收集数据 与同伴进行交流.
(3)小华利用派出所的户籍网随机调查了该地区10%的老年人,发现他们一年平均生病3次左右.你认为她的调查方式如何
可到当地派出所的户籍中抽样调查.
像小华这种随机调查的方式是收集数据常用的方法具有代表性,调查人数达到10%具有广泛性,方案可行.
典型例题
当堂检测
学习目标
课堂总结
总结:在现实生活中,当我们所要考察的总体中包含的个体数很多,有时总体中个数较多且总体是由有明显差异的几个部分组成时,我们应注意抽出的样本就必须有较强的代表性.每个部分都应抽取到,而且应注意各部分的比例.广泛性是指总体中的每个个体均有被选的可能.
典型例题
当堂检测
学习目标
课堂总结
三、概念剖析
简单随机抽样
为了获取能够客观反映问题的结果,通常按照总体中每个个体都有相等的被抽取机会的原则抽取样本,这种抽取样本的方法叫做简单随机抽样.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.下列哪些调查的样本缺乏代表性?
(1)在大学生中调查我国青年业余时间的主要娱乐方式;
(2)在公园调查老年人的健康情况;
(3)在学号为3的倍数的学生中调查2个班的数学成绩.
解:(1),(2)样本缺乏代表性;
学习目标
典型例题
当堂检测
课堂总结
(3)学号为3的倍数的学生包含2个班上各个层次的学生,故有代表性.
(2)在公园活动的老年人只是爱运动,身体相对健康的一部分,故缺乏代表性;
(1)只是片面的调查了大学生,大学生只是青年中学习上比较优秀的一部分,故缺乏代表性;
2.下列抽样调查中,结果能否较准确地反映总体的情况,为什么?
(1)某商场为了了解10月份的营业情况,从10月2日开始连续调查
了5天的营业情况;
(2)某公司为了了解自己产品的普及率,在市区某火车站对100名
流动人员进行调查分析.
解:(1)不能.因为10月2日~6日是国庆假期,商品卖出的多;
(2)不能.因为流动人口远远少于固定人口.
学习目标
典型例题
当堂检测
课堂总结
3.小李同学想了解湖边小区的家庭教育费用支出情况,调查了本校家住湖边小区的35名同学的家庭.并把这35个家庭的教育费用的平均数作为湖边小区家庭教育的平均费用的估计,你觉得合理吗?若不合理,请说明理由.并设计一个抽样调查的方案.
解:不合理.因为调查对象的局限性较大,都是自己学校的同学,是有孩子在校读书的家庭.
抽样调查可以按门牌号的奇、偶性来调查.
学习目标
典型例题
当堂检测
课堂总结
4.某县共种植小麦30 000公顷,其中山区、丘陵、平原种植面积的比为1:2:3.为了估计每公顷小麦的平均产量,请你设计一个代表性比较好的抽样调查方案.
解:为保证样本的代表性,需按照山区、丘陵、平原种植面积的比为1:2:3进行抽样;
学习目标
典型例题
当堂检测
课堂总结
对种植小麦按10%比例抽样调查;则样本中需包含山区500公顷,丘陵1000公顷,平原1500公顷;
然后在山区、丘陵、平原中随机抽取相应面积的小麦产量进行调查.
(答案不唯一)
样本的代表性:总体中个数较多且总体是由有明显差异的几个部分组成时,我们应注意抽出的样本就必须有较强的代表性.每个部分都应抽取到,而且应注意各部分的比例.
样本的广泛性:总体中的每个个体均有被选的可能.
典型例题
当堂检测
学习目标
课堂总结
简单随机抽样:为了获取能够客观反映问题的结果,通常按照总体中每个个体都有相等的被抽取机会的原则抽取样本.
4.2 简单随机抽样调查
第4章 数据的收集、整理与描述
1.知道抽样调查的优缺点,能判断抽取的样本是否具有代表性.
典型例题
当堂检测
学习目标
课堂总结
2.会设计恰当的抽样调查方案.
议一议:抽样调查的优点是什么?
典型例题
当堂检测
学习目标
课堂总结
抽样调查有缺点吗?应该注意些什么?
例1.为了了解你所在地区老年人的健康状况,你准备怎样收集数据?
下面分别是小明、小颖、小亮三个小组的调查结果:
我们小组在公园里调查了100名老年人,他们一年中生病的次数如图所示.
80
20
0
60
100
40
1至2次
3至6次
7次及以上
83
15
2
人数
生病次数
典型例题
当堂检测
学习目标
课堂总结
我们小组在医院调查了100名老年病人,他们一年中生病的次数如图所示.
我们小组调查了10名老年邻居,他们一年中生病的次数如下表所示.
生病的次数
人数
1至2次
4
3至6次
5
7次及以上
1
1至2次
7%
3至6次
24%
7次及以上
69%
典型例题
当堂检测
学习目标
课堂总结
(1)你同意他们的做法吗 说说你的理由.
小明调查的对象是选自公园里的老年人.常去公园里活动
的老年人,平时一定注意身体的保健,一定注意修身、养性、加强体育锻炼,所以身体较健康.
另一方面,公园建在城市里,相对于农村中的老年人去公园的较少.这100人中不同文化程度、不同职业、城市和乡村等不同层次的老人是否都有所选取,选取人数的比例是否合理,是否具有代表性与广泛性都是我们在收集数据中需要考虑的.
所以,小明收集的数据缺乏代表性和广泛性.
典型例题
当堂检测
学习目标
课堂总结
小颖收集的数据来自医院看病的100名老年人,这部分人相对体质较弱.我认为用这些数据得到的调查结果不准确,因为收集的数据缺乏代表性和广泛性.
小亮仅仅调查了10位老年人.因为样本太小了,所以不能据此推断某地区老年人的健康状况.
典型例题
当堂检测
学习目标
课堂总结
(2)为了了解该地区老年人的健康状况,你认为应当怎样收集数据 与同伴进行交流.
(3)小华利用派出所的户籍网随机调查了该地区10%的老年人,发现他们一年平均生病3次左右.你认为她的调查方式如何
可到当地派出所的户籍中抽样调查.
像小华这种随机调查的方式是收集数据常用的方法具有代表性,调查人数达到10%具有广泛性,方案可行.
典型例题
当堂检测
学习目标
课堂总结
总结:在现实生活中,当我们所要考察的总体中包含的个体数很多,有时总体中个数较多且总体是由有明显差异的几个部分组成时,我们应注意抽出的样本就必须有较强的代表性.每个部分都应抽取到,而且应注意各部分的比例.广泛性是指总体中的每个个体均有被选的可能.
典型例题
当堂检测
学习目标
课堂总结
三、概念剖析
简单随机抽样
为了获取能够客观反映问题的结果,通常按照总体中每个个体都有相等的被抽取机会的原则抽取样本,这种抽取样本的方法叫做简单随机抽样.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.下列哪些调查的样本缺乏代表性?
(1)在大学生中调查我国青年业余时间的主要娱乐方式;
(2)在公园调查老年人的健康情况;
(3)在学号为3的倍数的学生中调查2个班的数学成绩.
解:(1),(2)样本缺乏代表性;
学习目标
典型例题
当堂检测
课堂总结
(3)学号为3的倍数的学生包含2个班上各个层次的学生,故有代表性.
(2)在公园活动的老年人只是爱运动,身体相对健康的一部分,故缺乏代表性;
(1)只是片面的调查了大学生,大学生只是青年中学习上比较优秀的一部分,故缺乏代表性;
2.下列抽样调查中,结果能否较准确地反映总体的情况,为什么?
(1)某商场为了了解10月份的营业情况,从10月2日开始连续调查
了5天的营业情况;
(2)某公司为了了解自己产品的普及率,在市区某火车站对100名
流动人员进行调查分析.
解:(1)不能.因为10月2日~6日是国庆假期,商品卖出的多;
(2)不能.因为流动人口远远少于固定人口.
学习目标
典型例题
当堂检测
课堂总结
3.小李同学想了解湖边小区的家庭教育费用支出情况,调查了本校家住湖边小区的35名同学的家庭.并把这35个家庭的教育费用的平均数作为湖边小区家庭教育的平均费用的估计,你觉得合理吗?若不合理,请说明理由.并设计一个抽样调查的方案.
解:不合理.因为调查对象的局限性较大,都是自己学校的同学,是有孩子在校读书的家庭.
抽样调查可以按门牌号的奇、偶性来调查.
学习目标
典型例题
当堂检测
课堂总结
4.某县共种植小麦30 000公顷,其中山区、丘陵、平原种植面积的比为1:2:3.为了估计每公顷小麦的平均产量,请你设计一个代表性比较好的抽样调查方案.
解:为保证样本的代表性,需按照山区、丘陵、平原种植面积的比为1:2:3进行抽样;
学习目标
典型例题
当堂检测
课堂总结
对种植小麦按10%比例抽样调查;则样本中需包含山区500公顷,丘陵1000公顷,平原1500公顷;
然后在山区、丘陵、平原中随机抽取相应面积的小麦产量进行调查.
(答案不唯一)
样本的代表性:总体中个数较多且总体是由有明显差异的几个部分组成时,我们应注意抽出的样本就必须有较强的代表性.每个部分都应抽取到,而且应注意各部分的比例.
样本的广泛性:总体中的每个个体均有被选的可能.
典型例题
当堂检测
学习目标
课堂总结
简单随机抽样:为了获取能够客观反映问题的结果,通常按照总体中每个个体都有相等的被抽取机会的原则抽取样本.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
