6.3 特殊的平行四边形 第5课时课件 (共15张PPT)青岛版八年级下册数学
文档属性
| 名称 | 6.3 特殊的平行四边形 第5课时课件 (共15张PPT)青岛版八年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 10:16:15 | ||
图片预览




文档简介
(共15张PPT)
第6章 平行四边形
6.3 特殊的平行四边形 第5课时
1.理解正方形的定义、性质和判定方法.
2.理解正方形与平行四边形、矩形、菱形的关系.
3.能运用正方形性质和判定方法解决相关几何问题.
任务一:理解正方形的定义、探索正方形性质和判定方法.
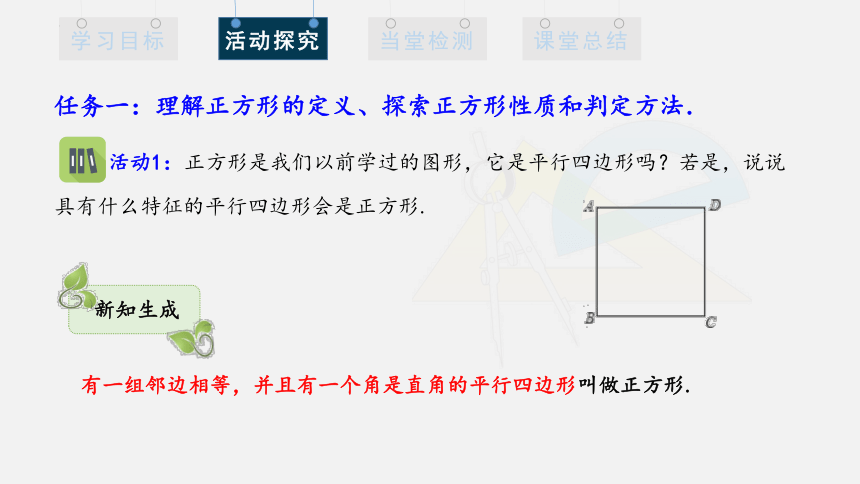
活动1:正方形是我们以前学过的图形,它是平行四边形吗?若是,说说具有什么特征的平行四边形会是正方形.
新知生成
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
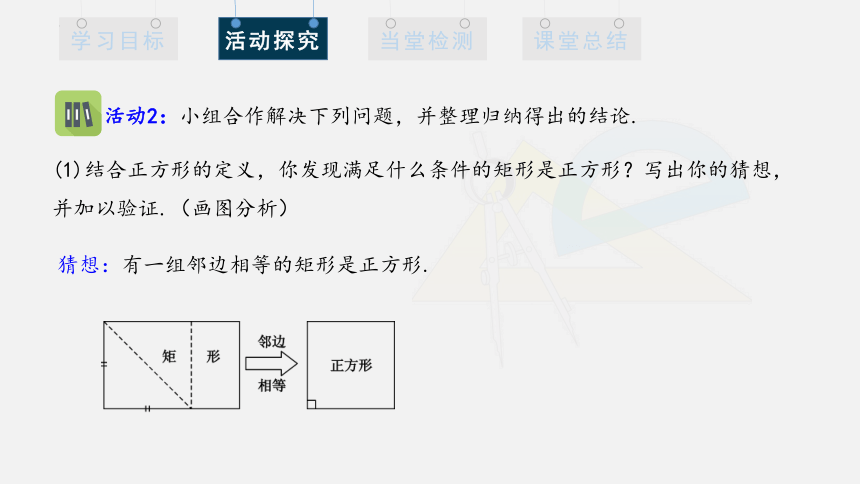
猜想:有一组邻边相等的矩形是正方形.
(1)结合正方形的定义,你发现满足什么条件的矩形是正方形?写出你的猜想,并加以验证.(画图分析)
活动2:小组合作解决下列问题,并整理归纳得出的结论.
猜想:有一组邻边相等的矩形是正方形.
已知:如图,在矩形ABCD中,AB=AD,
求证:矩形ABCD是正方形
证明:∵四边形ABCD是矩形,
∴∠B=90°,四边形ABCD也是平行四边形,
∵AB=AD,
∴四边形ABCD是正方形(正方形的定义)
结论:
有一组邻边相等的矩形是正方形.
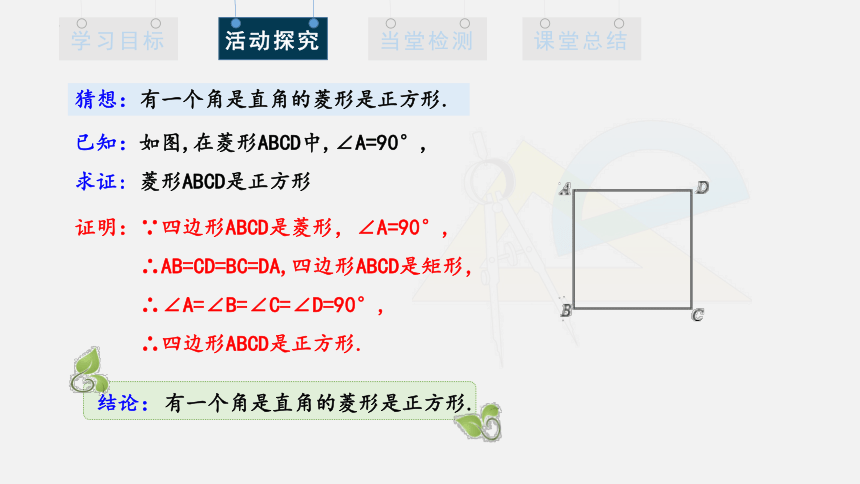
猜想:有一个角是直角的菱形是正方形.
(2)结合正方形的定义,思考满足什么条件的菱形是正方形?写出你的猜想,并加以验证.(画图分析)
猜想:有一个角是直角的菱形是正方形.
已知:如图,在菱形ABCD中,∠A=90°,
求证: 菱形ABCD是正方形
证明:∵四边形ABCD是菱形,∠A=90°,
∴AB=CD=BC=DA,四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD是正方形.
结论:
有一个角是直角的菱形是正方形.
(3)思考平行四边形、矩形、菱形、正方形的从属关系,完成下列关系图.
平行四边形
菱形
矩形
正方形
平行四边形、矩形、菱形、正方形的关系图
四边形
(1)正方形有哪些性质?它是不是轴对称图形?若是,有几条对称轴.
(2)如何判定一个四边形是不是正方形?
根据平行四边形、矩形、菱形、正方形的关系,解决下列问题:
小组讨论
活动小结
正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.
轴对称性:正方形是轴对称图形,有4条对称轴(如右图).
边角性质:四个角都是直角;四条边都相等;对角线相等,并且互相垂直平分.
+
(2)先判定菱形,再判定矩形:
一个角是直角
+
(1)先判定矩形,再判定菱形:
一组邻边相等
正方形
正方形
正方形的判定思路:
从四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD,选两个作为补充条件,使 ABCD为正方形(如图).下列四种选法,其中错误的是( ).
A.①② B.②③ C.①③ D.②④
B
练一练
任务二:运用正方形性质和判定方法解决相关几何问题.
活动:小组合作解决下列问题,简要说说求解过程中用到的性质和方法.
证明:连接PA,∵PM⊥AD,PN⊥AB,四边形ABCD是正方形,
∴∠PMA=∠PNA=∠A=90°,∴四边形PMAN是矩形,∴PA=MN,∵P是正方形ABCD对角线上一点,∴AD=CD,∠PDA=∠PDC,PD=DP,∴△PAD≌△PCD(SAS),∴PA=PC,∴MN=PC.
O
或在得出PA=MN后,再连接AC,交BD于O,可知BD是AC的垂直平分线.∴PA=PC ,∴MN=PC.
如图,正方形ABCD中,点P是对角线BD上一点,PM⊥AD,PN⊥AB,垂足为M、N.
求证:MN=PC.
1.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且垂直平分
C.对角线互相平分
D.四边相等,四个角相等
C
证明:∵∠C=90°,DE⊥BC于E,DF⊥AC于F,
∴四边形CFDE是矩形,
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,
∴四边形CFDE是正方形.(有一组邻边相等的矩形是正方形)
2.如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.正方形的定义及性质
2.正方形的判定方法
第6章 平行四边形
6.3 特殊的平行四边形 第5课时
1.理解正方形的定义、性质和判定方法.
2.理解正方形与平行四边形、矩形、菱形的关系.
3.能运用正方形性质和判定方法解决相关几何问题.
任务一:理解正方形的定义、探索正方形性质和判定方法.
活动1:正方形是我们以前学过的图形,它是平行四边形吗?若是,说说具有什么特征的平行四边形会是正方形.
新知生成
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
猜想:有一组邻边相等的矩形是正方形.
(1)结合正方形的定义,你发现满足什么条件的矩形是正方形?写出你的猜想,并加以验证.(画图分析)
活动2:小组合作解决下列问题,并整理归纳得出的结论.
猜想:有一组邻边相等的矩形是正方形.
已知:如图,在矩形ABCD中,AB=AD,
求证:矩形ABCD是正方形
证明:∵四边形ABCD是矩形,
∴∠B=90°,四边形ABCD也是平行四边形,
∵AB=AD,
∴四边形ABCD是正方形(正方形的定义)
结论:
有一组邻边相等的矩形是正方形.
猜想:有一个角是直角的菱形是正方形.
(2)结合正方形的定义,思考满足什么条件的菱形是正方形?写出你的猜想,并加以验证.(画图分析)
猜想:有一个角是直角的菱形是正方形.
已知:如图,在菱形ABCD中,∠A=90°,
求证: 菱形ABCD是正方形
证明:∵四边形ABCD是菱形,∠A=90°,
∴AB=CD=BC=DA,四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD是正方形.
结论:
有一个角是直角的菱形是正方形.
(3)思考平行四边形、矩形、菱形、正方形的从属关系,完成下列关系图.
平行四边形
菱形
矩形
正方形
平行四边形、矩形、菱形、正方形的关系图
四边形
(1)正方形有哪些性质?它是不是轴对称图形?若是,有几条对称轴.
(2)如何判定一个四边形是不是正方形?
根据平行四边形、矩形、菱形、正方形的关系,解决下列问题:
小组讨论
活动小结
正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.
轴对称性:正方形是轴对称图形,有4条对称轴(如右图).
边角性质:四个角都是直角;四条边都相等;对角线相等,并且互相垂直平分.
+
(2)先判定菱形,再判定矩形:
一个角是直角
+
(1)先判定矩形,再判定菱形:
一组邻边相等
正方形
正方形
正方形的判定思路:
从四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD,选两个作为补充条件,使 ABCD为正方形(如图).下列四种选法,其中错误的是( ).
A.①② B.②③ C.①③ D.②④
B
练一练
任务二:运用正方形性质和判定方法解决相关几何问题.
活动:小组合作解决下列问题,简要说说求解过程中用到的性质和方法.
证明:连接PA,∵PM⊥AD,PN⊥AB,四边形ABCD是正方形,
∴∠PMA=∠PNA=∠A=90°,∴四边形PMAN是矩形,∴PA=MN,∵P是正方形ABCD对角线上一点,∴AD=CD,∠PDA=∠PDC,PD=DP,∴△PAD≌△PCD(SAS),∴PA=PC,∴MN=PC.
O
或在得出PA=MN后,再连接AC,交BD于O,可知BD是AC的垂直平分线.∴PA=PC ,∴MN=PC.
如图,正方形ABCD中,点P是对角线BD上一点,PM⊥AD,PN⊥AB,垂足为M、N.
求证:MN=PC.
1.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且垂直平分
C.对角线互相平分
D.四边相等,四个角相等
C
证明:∵∠C=90°,DE⊥BC于E,DF⊥AC于F,
∴四边形CFDE是矩形,
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,
∴四边形CFDE是正方形.(有一组邻边相等的矩形是正方形)
2.如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.正方形的定义及性质
2.正方形的判定方法
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
