1.2 怎样判定三角形全等 第1课时课件(共16张PPT) 青岛版八年级上册数学
文档属性
| 名称 | 1.2 怎样判定三角形全等 第1课时课件(共16张PPT) 青岛版八年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 10:17:54 | ||
图片预览




文档简介
(共16张PPT)
第1章 全等三角形
1.2 怎样判定三角形全等 第1课时
1.理解确定两个三角形全等至少需要三个条件.
2.掌握三角形全等的判定方法1——边角边.
3.能运用“边角边”解决简单的实际问题.
任务一:掌握三角形全等的判定方法1——边角边.
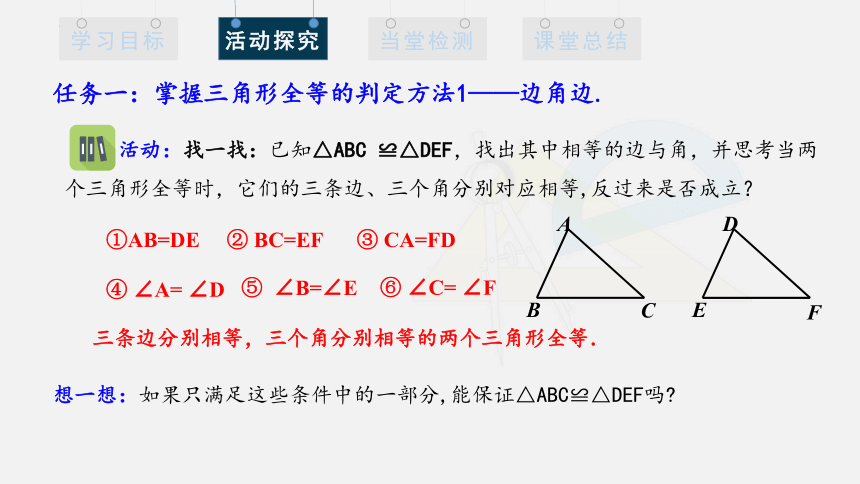
活动:找一找:已知△ABC ≌△DEF,找出其中相等的边与角,并思考当两个三角形全等时,它们的三条边、三个角分别对应相等,反过来是否成立?
三条边分别相等,三个角分别相等的两个三角形全等.
想一想:如果只满足这些条件中的一部分,能保证△ABC≌△DEF吗
A
B
C
D
E
F
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
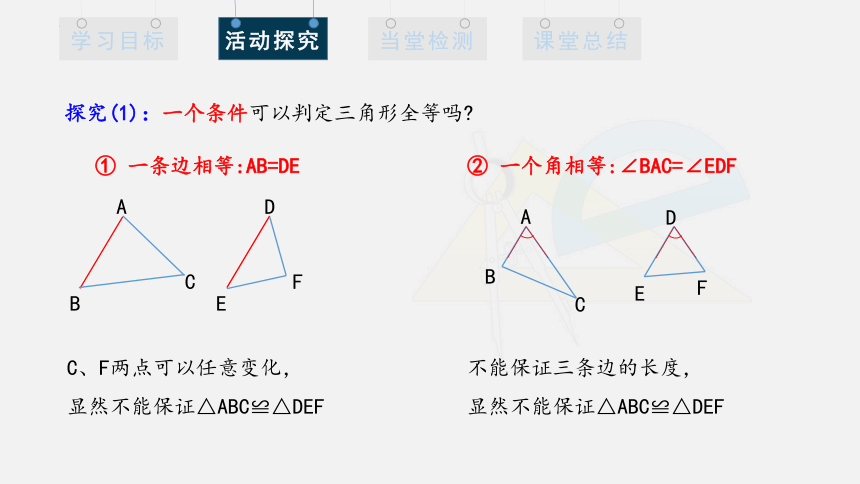
① 一条边相等:AB=DE
A
B
C
D
E
F
C、F两点可以任意变化,
显然不能保证△ABC≌△DEF
② 一个角相等:∠BAC=∠EDF
A
B
C
D
E
F
不能保证三条边的长度,
显然不能保证△ABC≌△DEF
探究(1):一个条件可以判定三角形全等吗
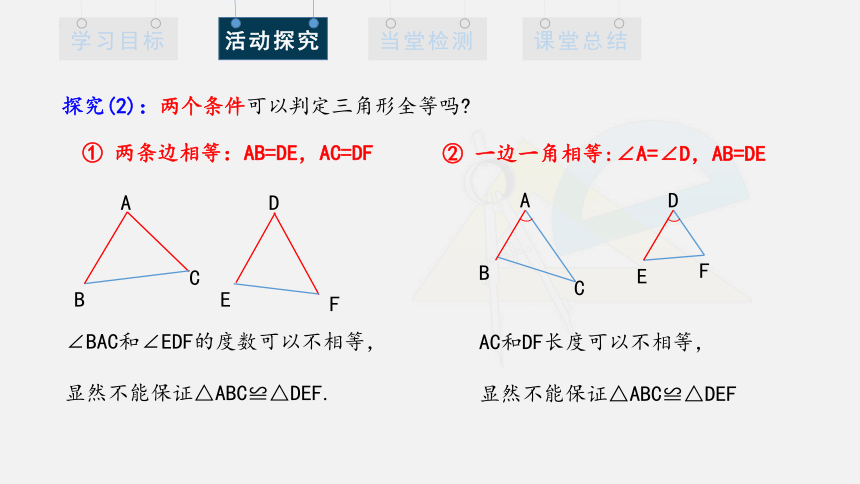
探究(2):两个条件可以判定三角形全等吗
① 两条边相等:AB=DE,AC=DF
A
B
C
D
E
F
∠BAC和∠EDF的度数可以不相等,显然不能保证△ABC≌△DEF.
② 一边一角相等:∠A=∠D,AB=DE
A
B
C
D
E
F
AC和DF长度可以不相等,
显然不能保证△ABC≌△DEF
③ 两个角相等
根据三角形内角和定理,可推出这两个三角形三个角都相等.
但三个角都相等仍然无法保证两个三角形全等,如下图.
E点为AB边上一点,作EF∥BC交AC于F;
△ABC与△AEF三个角都相等,但△ABC与△AEF不全等.
A
B
C
E
F
探究(3):三个条件可以判定三角形全等吗
① 三个条件可以分为几种情况呢?
a.都给角:给三个角(情况同两个角相等)
b.都给边:给三条边
c.既给角,又给边:①给一条边,两个角
②给两条边,一个角
② 探究两条边和一个角相等的两个三角形是否会全等?
a.请动手画画,你能得出一个三角形中两条边与一个角的位置有几种可能性?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
平移△ABC,使点B与B′重合,BC落在B′C′上,点A、A′在BC同侧,因BC=B′C′,故点C、C′重合.因∠B=∠B′,故射线BA与BA′重合,点A、点A′重合.所以△ABC ≌△A′B′C′.
b.每位同学在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 通过适当的叠合方式,判断这两个三角形是否全等
A
B
C
c.如图,把一长一短两根木棍的一端固定在一起摆出△ABC.长木棍固定,转动短木棍,得到△ABD.可知这两个三角形的哪些边、角相等?它们全等吗?
△ABC和△ABD满足AB=AB ,AC=AD,∠B=∠B,但△ABC与△ABD不全等.
B
A
C
D
d.由以上解题过程,你能得出什么结论?
活动小结
“边角边”判定三角形全等
文字语言:两边及其夹角分别相等的两个三角形全等(简写为“边角边”或“SAS”)
数学语言:在△ABC和△ DEF中,
A
B
C
D
E
F
AB=DE,
∠A=∠D,
AC=DF,
所以△ABC ≌△ DEF(SAS).
注意:两边和其中一边的对角相等(边边角)不能保证两个三角形全等.
练一练
如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.试说明:△AFD≌△CEB.
F
A
B
D
C
E
解:因为AD//BC,
所以∠A=∠C,
在△AFD和△CEB中,
所以△AFD≌△CEB(SAS).
因为AE=CF,
所以AE+EF=CF+EF,即AF=CE.
AD=CB
∠A=∠C
AF=CE
(已知),
(已证),
(已证),
活动:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC、BC并延长到点D、E,使CD=CA、CE=CB. 连接DE,量出DE的长就是A、B的距离,这是为什么
C
·
A
E
D
B
解:在△ABC 和△DEC 中:AC = DC、
CB=EC(已知),∠ACB = ∠DCE(对顶角相等),
所以 △ABC≌△DEC (SAS)
所以 AB = DE(全等三角形的对应边相等)
任务二:运用“边角边”解决简单的实际问题.
1.如图,已知AC=BD,可添加一个条件 ,使得△ABC和△BAD全等.
A
B
C
D
∠CAB=∠DBA
2. 小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明说能不用测量就知道EH=FH,他的说法正确吗?为什么?
解:正确,理由如下:
在△EDH和△FDH中,ED = FD、(已知)
∠EDH =∠FDH(已知)、DH = DH(公共边),
由SAS,所以△EDH ≌ △FDH.
所以EH = FH(全等三角形对应边相等).
E
F
D
H
针对本节课的关键词“边角边”,你能说说学到了哪些知识吗?
三角形全等的判定
确定两个三角形全等至少需要三个条件
判定方法1-SAS
两边及其夹角分别相等的两个三角形全等
SAS的应用
第1章 全等三角形
1.2 怎样判定三角形全等 第1课时
1.理解确定两个三角形全等至少需要三个条件.
2.掌握三角形全等的判定方法1——边角边.
3.能运用“边角边”解决简单的实际问题.
任务一:掌握三角形全等的判定方法1——边角边.
活动:找一找:已知△ABC ≌△DEF,找出其中相等的边与角,并思考当两个三角形全等时,它们的三条边、三个角分别对应相等,反过来是否成立?
三条边分别相等,三个角分别相等的两个三角形全等.
想一想:如果只满足这些条件中的一部分,能保证△ABC≌△DEF吗
A
B
C
D
E
F
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
① 一条边相等:AB=DE
A
B
C
D
E
F
C、F两点可以任意变化,
显然不能保证△ABC≌△DEF
② 一个角相等:∠BAC=∠EDF
A
B
C
D
E
F
不能保证三条边的长度,
显然不能保证△ABC≌△DEF
探究(1):一个条件可以判定三角形全等吗
探究(2):两个条件可以判定三角形全等吗
① 两条边相等:AB=DE,AC=DF
A
B
C
D
E
F
∠BAC和∠EDF的度数可以不相等,显然不能保证△ABC≌△DEF.
② 一边一角相等:∠A=∠D,AB=DE
A
B
C
D
E
F
AC和DF长度可以不相等,
显然不能保证△ABC≌△DEF
③ 两个角相等
根据三角形内角和定理,可推出这两个三角形三个角都相等.
但三个角都相等仍然无法保证两个三角形全等,如下图.
E点为AB边上一点,作EF∥BC交AC于F;
△ABC与△AEF三个角都相等,但△ABC与△AEF不全等.
A
B
C
E
F
探究(3):三个条件可以判定三角形全等吗
① 三个条件可以分为几种情况呢?
a.都给角:给三个角(情况同两个角相等)
b.都给边:给三条边
c.既给角,又给边:①给一条边,两个角
②给两条边,一个角
② 探究两条边和一个角相等的两个三角形是否会全等?
a.请动手画画,你能得出一个三角形中两条边与一个角的位置有几种可能性?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
平移△ABC,使点B与B′重合,BC落在B′C′上,点A、A′在BC同侧,因BC=B′C′,故点C、C′重合.因∠B=∠B′,故射线BA与BA′重合,点A、点A′重合.所以△ABC ≌△A′B′C′.
b.每位同学在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 通过适当的叠合方式,判断这两个三角形是否全等
A
B
C
c.如图,把一长一短两根木棍的一端固定在一起摆出△ABC.长木棍固定,转动短木棍,得到△ABD.可知这两个三角形的哪些边、角相等?它们全等吗?
△ABC和△ABD满足AB=AB ,AC=AD,∠B=∠B,但△ABC与△ABD不全等.
B
A
C
D
d.由以上解题过程,你能得出什么结论?
活动小结
“边角边”判定三角形全等
文字语言:两边及其夹角分别相等的两个三角形全等(简写为“边角边”或“SAS”)
数学语言:在△ABC和△ DEF中,
A
B
C
D
E
F
AB=DE,
∠A=∠D,
AC=DF,
所以△ABC ≌△ DEF(SAS).
注意:两边和其中一边的对角相等(边边角)不能保证两个三角形全等.
练一练
如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.试说明:△AFD≌△CEB.
F
A
B
D
C
E
解:因为AD//BC,
所以∠A=∠C,
在△AFD和△CEB中,
所以△AFD≌△CEB(SAS).
因为AE=CF,
所以AE+EF=CF+EF,即AF=CE.
AD=CB
∠A=∠C
AF=CE
(已知),
(已证),
(已证),
活动:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC、BC并延长到点D、E,使CD=CA、CE=CB. 连接DE,量出DE的长就是A、B的距离,这是为什么
C
·
A
E
D
B
解:在△ABC 和△DEC 中:AC = DC、
CB=EC(已知),∠ACB = ∠DCE(对顶角相等),
所以 △ABC≌△DEC (SAS)
所以 AB = DE(全等三角形的对应边相等)
任务二:运用“边角边”解决简单的实际问题.
1.如图,已知AC=BD,可添加一个条件 ,使得△ABC和△BAD全等.
A
B
C
D
∠CAB=∠DBA
2. 小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明说能不用测量就知道EH=FH,他的说法正确吗?为什么?
解:正确,理由如下:
在△EDH和△FDH中,ED = FD、(已知)
∠EDH =∠FDH(已知)、DH = DH(公共边),
由SAS,所以△EDH ≌ △FDH.
所以EH = FH(全等三角形对应边相等).
E
F
D
H
针对本节课的关键词“边角边”,你能说说学到了哪些知识吗?
三角形全等的判定
确定两个三角形全等至少需要三个条件
判定方法1-SAS
两边及其夹角分别相等的两个三角形全等
SAS的应用
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
