【练闯考】2015(秋)华师大版九年级数学上册课件:23.4 中位线
文档属性
| 名称 | 【练闯考】2015(秋)华师大版九年级数学上册课件:23.4 中位线 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 09:45:03 | ||
图片预览





文档简介
课件14张PPT。23.4 中位线1.连结三角形_____________的线段叫做三角形的中位线.
2.三角形的中位线__________第三边,并且等于第三边的_____.
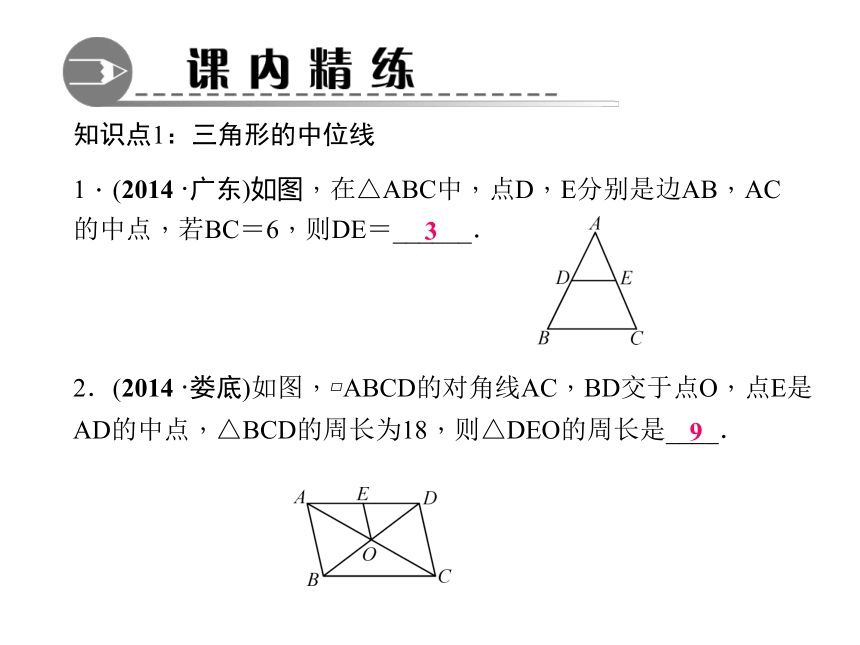
3.一个三角形有三条中线,它们相交于_______,这个点就是_________________________,重心与一边中点的连线的长是对应中线长的____.两边中心平行于一半一点三角形的重心知识点1:三角形的中位线1.(2014·广东)如图,在△ABC中,点D,E分别是边AB,AC的中点,若BC=6,则DE=______.32.(2014·娄底)如图,?ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是____.93.(2014·宜昌)如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24 m B.MN∥AB
C.△CMN∽△CAB D.CM∶MA=1∶2D4.(2014·南平)如图,△ABC中,AD,BE是两条中线,则S△EDC∶S△ABC=( )
A.1∶2 B.2∶3 C.1∶3 D.1∶4D5.一个三角形的周长是36 cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A.6 cm B.12 cm C.18 cm D.36 cm
6.如图,在△ABC中,点D,E分别是边AC,AB的中点,连接BD.若BD平分∠ABC,则下列结论错误的是( )
A.BC=2BE B.∠A=∠EDA
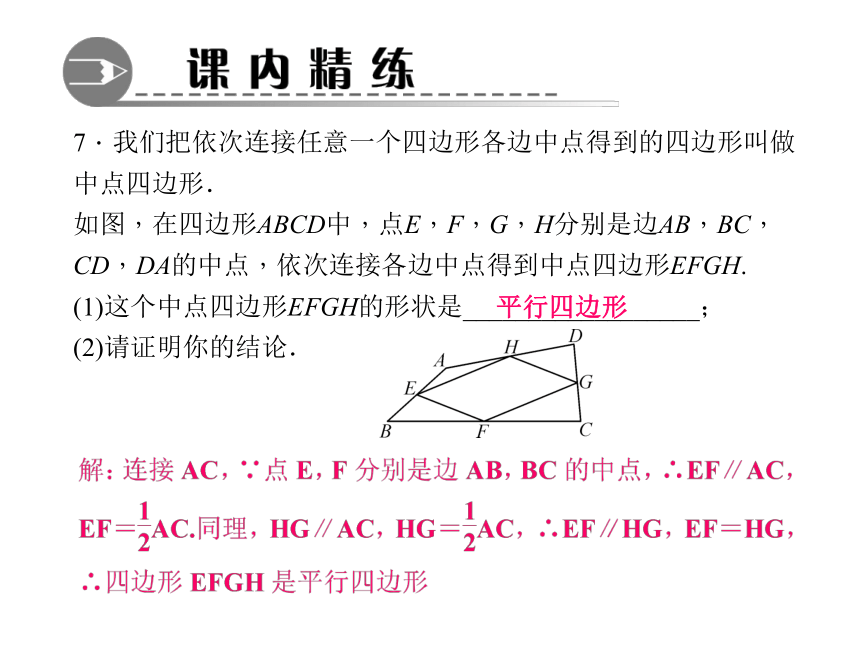
C.BC=2AD D.BD⊥ACCC7.我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是__________________;
(2)请证明你的结论.平行四边形知识点2:三角形的重心8.在△ABC中,AD是BC边上的中线,点G是重心,如果AG=8,那么线段DG的长为( )
A.2 B.4 C.6 D.8BB 11.已知,在△ABC中,点G为重心,过点G的直线MN∥AB,交AC于点M,交BC于点N,AB=7,求MN的长.(提示:连接CG并延长CG交AB于点H)12.如图,AB∥CD,点E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )
A.4 B.3 C.2 D.1 D13.如图,DE是△ABC的中位线,点M,N分别是BD,CE的中点,MN=6,则BC=____.814.在△ABC中,点G为重心,若BC边上的高为6,则点G到BC边的距离为____. 215.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB=5,AC=2,则DF的长为____.16.如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是____.1117.如图,点E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF.
求证:AB=2OF.解:易证F点为BC边的中点,由中位线定理可证AB=2OF18.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F.点E是AB的中点,连接EF.
(1)求证:EF∥BC;
(2)若△ABD的面积是6,求四边形BDFE的面积.解:(1)易证点F为AD的中点,由EF为△ABD的中位线得EF∥BC 19.如图,在四边形ABCD中,AB=CD,点M,N,P分别是AD,BC,BD的中点,∠ABD=20°,∠BDC=70°,试求∠PNM的度数.20.如图,在△ABC中,点D,E分别是AB,AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DF交于点O.若△ADE的面积为S,试求四边形BOGC的面积.
2.三角形的中位线__________第三边,并且等于第三边的_____.
3.一个三角形有三条中线,它们相交于_______,这个点就是_________________________,重心与一边中点的连线的长是对应中线长的____.两边中心平行于一半一点三角形的重心知识点1:三角形的中位线1.(2014·广东)如图,在△ABC中,点D,E分别是边AB,AC的中点,若BC=6,则DE=______.32.(2014·娄底)如图,?ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是____.93.(2014·宜昌)如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24 m B.MN∥AB
C.△CMN∽△CAB D.CM∶MA=1∶2D4.(2014·南平)如图,△ABC中,AD,BE是两条中线,则S△EDC∶S△ABC=( )
A.1∶2 B.2∶3 C.1∶3 D.1∶4D5.一个三角形的周长是36 cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A.6 cm B.12 cm C.18 cm D.36 cm
6.如图,在△ABC中,点D,E分别是边AC,AB的中点,连接BD.若BD平分∠ABC,则下列结论错误的是( )
A.BC=2BE B.∠A=∠EDA
C.BC=2AD D.BD⊥ACCC7.我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是__________________;
(2)请证明你的结论.平行四边形知识点2:三角形的重心8.在△ABC中,AD是BC边上的中线,点G是重心,如果AG=8,那么线段DG的长为( )
A.2 B.4 C.6 D.8BB 11.已知,在△ABC中,点G为重心,过点G的直线MN∥AB,交AC于点M,交BC于点N,AB=7,求MN的长.(提示:连接CG并延长CG交AB于点H)12.如图,AB∥CD,点E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )
A.4 B.3 C.2 D.1 D13.如图,DE是△ABC的中位线,点M,N分别是BD,CE的中点,MN=6,则BC=____.814.在△ABC中,点G为重心,若BC边上的高为6,则点G到BC边的距离为____. 215.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB=5,AC=2,则DF的长为____.16.如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是____.1117.如图,点E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF.
求证:AB=2OF.解:易证F点为BC边的中点,由中位线定理可证AB=2OF18.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F.点E是AB的中点,连接EF.
(1)求证:EF∥BC;
(2)若△ABD的面积是6,求四边形BDFE的面积.解:(1)易证点F为AD的中点,由EF为△ABD的中位线得EF∥BC 19.如图,在四边形ABCD中,AB=CD,点M,N,P分别是AD,BC,BD的中点,∠ABD=20°,∠BDC=70°,试求∠PNM的度数.20.如图,在△ABC中,点D,E分别是AB,AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DF交于点O.若△ADE的面积为S,试求四边形BOGC的面积.
