北师大版六年级下册数学1. 5圆柱的体积课件(共21张PPT)
文档属性
| 名称 | 北师大版六年级下册数学1. 5圆柱的体积课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 06:22:12 | ||
图片预览




文档简介
(共21张PPT)
北师大版六年级数学下册
圆柱的体积(1)
汇报人:XXX 时间:XXXXX
一 圆柱与圆锥
结合具体情境,探索并掌握圆柱体积的计算方法,并能运用计算公式解决简单的实际问题。
经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,渗透数学思想,体验数学研究的方法。
感受数学思考过程,获得成功的喜悦。
什么是体积?
物体所占空间的大小是物体的体积。
一个杯子能装多少毫升水呢?
实际上都需要求圆柱的体积。
这么粗的柱子,需要多少木材呢?
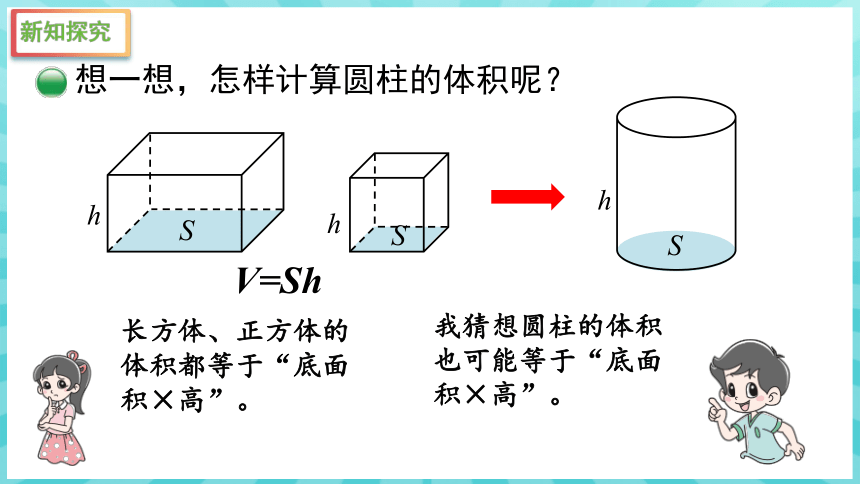
想一想,怎样计算圆柱的体积呢?
我猜想圆柱的体积也可能等于“底面积×高”。
长方体、正方体的体积都等于“底面积×高”。
V=Sh
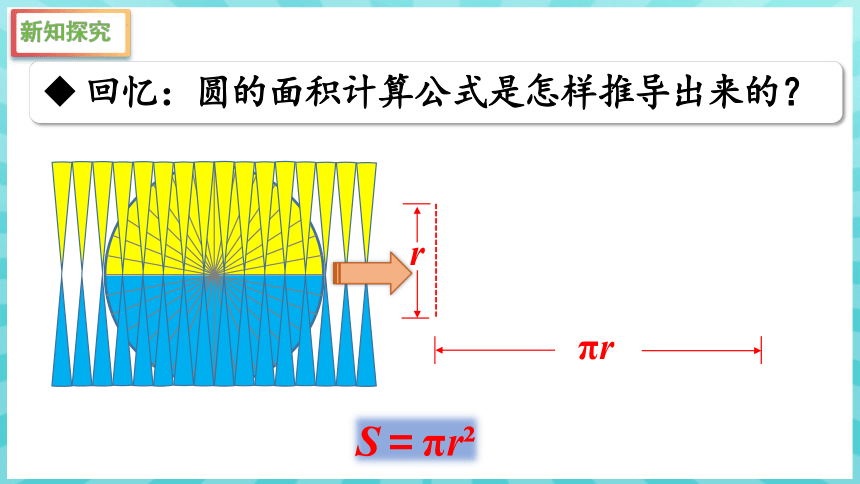
回忆:圆的面积计算公式是怎样推导出来的?
r
S=πr
πr
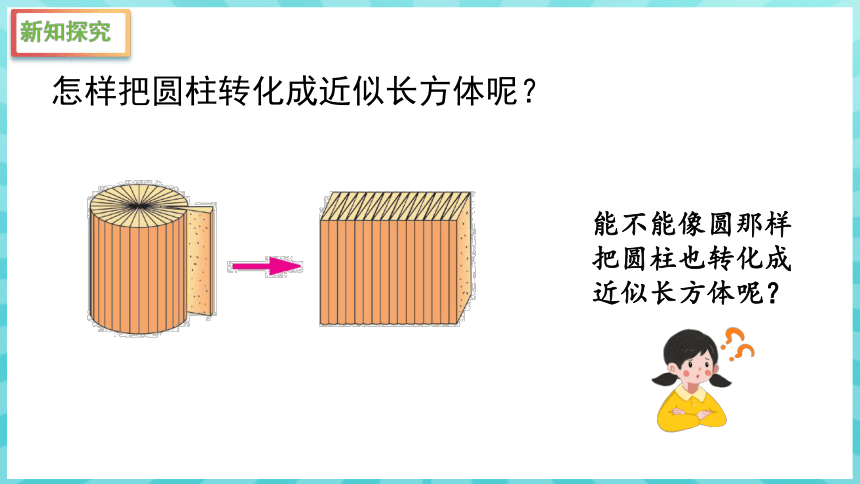
能不能像圆那样把圆柱也转化成近似长方体呢?
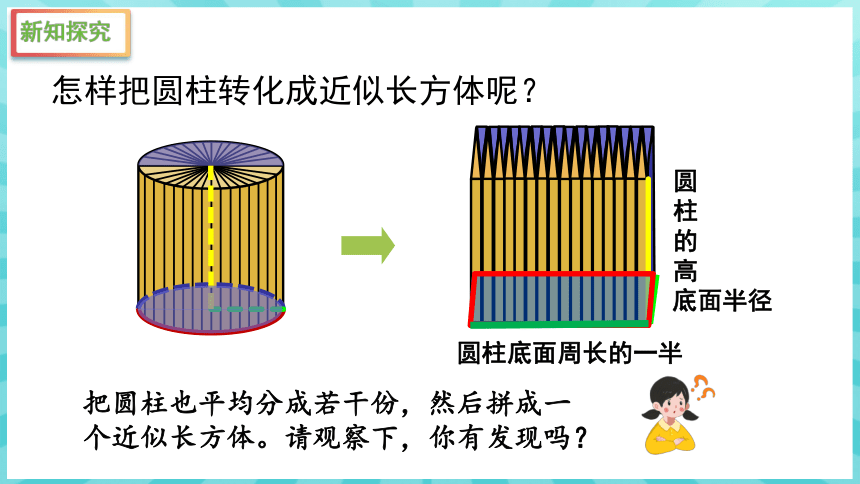
怎样把圆柱转化成近似长方体呢?
把圆柱也平均分成若干份,然后拼成一个近似长方体。请观察下,你有发现吗?
圆柱底面周长的一半
圆柱的高
底面半径
怎样把圆柱转化成近似长方体呢?
V S h
V = Sh
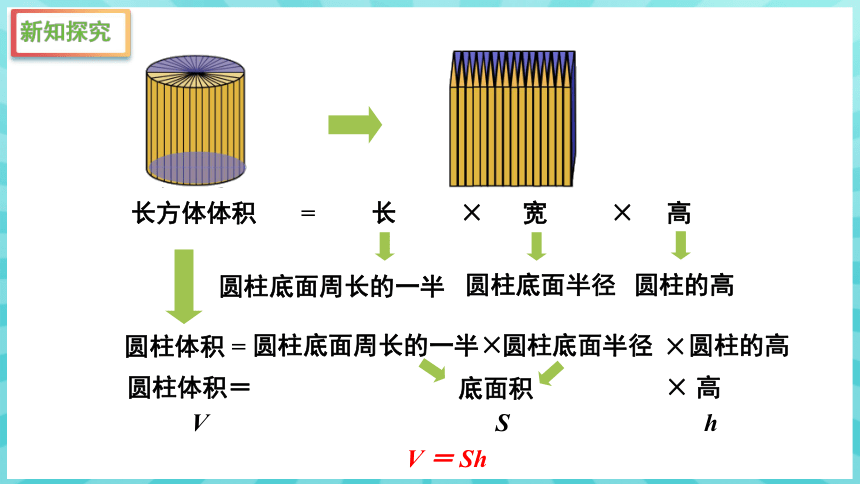
长方体体积 = 长 × 宽 × 高
圆柱体积 =
圆柱底面周长的一半
圆柱底面半径
圆柱的高
圆柱底面周长的一半
圆柱底面半径
圆柱的高
×
×
底面积
× 高
圆柱体积=
尝试解决刚才的问题:
3.14×0.42×5
=3.14×(0.16×5)
=3.14×0.8
=2.512(m3)
答:需要2.512立方米木材。
这么粗的柱子,需要多少木材呢?
一根柱子的底面半径为0.4 m,高为5 m。
3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:这个杯子能装452.16毫升水。
从水杯里面量,水杯的底面直径是6 cm,高是16 cm。
尝试解决刚才的问题:
一个杯子能装多少毫升水呢?
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π(d÷2)2h
已知底面周长和高:V = π(C÷2π)2h
根据不同的条件可以推导出不同的公式。
我会推导:
为了推导圆柱的体积,我们可以将圆柱转化为( ),长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( ),长方体的体积等于圆柱的( )。
因为长方体的体积=( )×( ),所以圆柱的体积=( )×( )。
长方体
底面积
高
体积
底面积
高
底面积
高
1.
分别计算下列各图形的体积,再说说这几个图形体积计算方法之间的联系。
4×3×8
=12×8
=96(cm3)
6×6×6
=36×6
=216(cm3)
3.14×(5÷2)2×8
=19.625×8
=157(cm3)
都可以用底面积乘高来求这三个图形的体积。
2.
计算下面各圆柱的体积。
V =πr 2h
3.14×12×5
=3.14×5
=15.7(cm3)
V =π(d÷2)2h
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(dm3)
V =Sh
60×4=240(cm3)
3.
这个杯子能否装下 3000 mL 的牛奶?
3.14×(14÷2)2×20
=3.14×49×20
=153.86×20
=3077.2(cm3)
=3077.2(mL)
3077.2mL >3000mL
答:这个杯子能装下 3000 mL 的牛奶。
4.
下面的长方体和圆柱哪个体积大?
4×6×4
=24×4
=96(dm3)
96 dm > 75.36 dm3
答:长方体的体积大。
3.14×22×6
=3.14×4×6
=12.56×6
=75.36(dm3)
5.
如图,求出小铁块的体积。
解法一:
3.14×(10÷2)2×(7-5)
=3.14×25×2
=78.5×2
=157 ( cm3 )
5cm
7cm
10cm
10cm
6.
5cm
7cm
10cm
10cm
6.
3.14×(10÷2)2×5
=3.14×25×5
=78.5×5
=392.5(cm3)
3.14×(10÷2)2×7
=3.14×25×7
=78.5×7
=549.5(cm3)
549.5-392.5=157( cm3 )
解法二:
如图,求出小铁块的体积。
奇思有一个圆柱形的水杯,水杯的底面直径是4厘米,高是10厘米,有资料显示:每人每天的正常饮水量大约是1立方分米,奇思一天要喝几杯水?
3.14×(4÷2)2×10
=12.56×10
=125.6(立方厘米)=0.1256(立方分米)
1÷0.1256≈8(杯)
答:奇思一天大约要喝8杯水。
7.
圆柱的体积是怎么计算的呢,你能写出圆柱的体积计算公式吗?
要计算一个圆柱的体积,只要用它的底面面积乘以它的高就可以了。
圆柱的体积计算公式是:
圆柱的体积=底面积×高
V=Sh
北师大版六年级数学下册
圆柱的体积(1)
汇报人:XXX 时间:XXXXX
一 圆柱与圆锥
结合具体情境,探索并掌握圆柱体积的计算方法,并能运用计算公式解决简单的实际问题。
经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,渗透数学思想,体验数学研究的方法。
感受数学思考过程,获得成功的喜悦。
什么是体积?
物体所占空间的大小是物体的体积。
一个杯子能装多少毫升水呢?
实际上都需要求圆柱的体积。
这么粗的柱子,需要多少木材呢?
想一想,怎样计算圆柱的体积呢?
我猜想圆柱的体积也可能等于“底面积×高”。
长方体、正方体的体积都等于“底面积×高”。
V=Sh
回忆:圆的面积计算公式是怎样推导出来的?
r
S=πr
πr
能不能像圆那样把圆柱也转化成近似长方体呢?
怎样把圆柱转化成近似长方体呢?
把圆柱也平均分成若干份,然后拼成一个近似长方体。请观察下,你有发现吗?
圆柱底面周长的一半
圆柱的高
底面半径
怎样把圆柱转化成近似长方体呢?
V S h
V = Sh
长方体体积 = 长 × 宽 × 高
圆柱体积 =
圆柱底面周长的一半
圆柱底面半径
圆柱的高
圆柱底面周长的一半
圆柱底面半径
圆柱的高
×
×
底面积
× 高
圆柱体积=
尝试解决刚才的问题:
3.14×0.42×5
=3.14×(0.16×5)
=3.14×0.8
=2.512(m3)
答:需要2.512立方米木材。
这么粗的柱子,需要多少木材呢?
一根柱子的底面半径为0.4 m,高为5 m。
3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:这个杯子能装452.16毫升水。
从水杯里面量,水杯的底面直径是6 cm,高是16 cm。
尝试解决刚才的问题:
一个杯子能装多少毫升水呢?
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π(d÷2)2h
已知底面周长和高:V = π(C÷2π)2h
根据不同的条件可以推导出不同的公式。
我会推导:
为了推导圆柱的体积,我们可以将圆柱转化为( ),长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( ),长方体的体积等于圆柱的( )。
因为长方体的体积=( )×( ),所以圆柱的体积=( )×( )。
长方体
底面积
高
体积
底面积
高
底面积
高
1.
分别计算下列各图形的体积,再说说这几个图形体积计算方法之间的联系。
4×3×8
=12×8
=96(cm3)
6×6×6
=36×6
=216(cm3)
3.14×(5÷2)2×8
=19.625×8
=157(cm3)
都可以用底面积乘高来求这三个图形的体积。
2.
计算下面各圆柱的体积。
V =πr 2h
3.14×12×5
=3.14×5
=15.7(cm3)
V =π(d÷2)2h
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(dm3)
V =Sh
60×4=240(cm3)
3.
这个杯子能否装下 3000 mL 的牛奶?
3.14×(14÷2)2×20
=3.14×49×20
=153.86×20
=3077.2(cm3)
=3077.2(mL)
3077.2mL >3000mL
答:这个杯子能装下 3000 mL 的牛奶。
4.
下面的长方体和圆柱哪个体积大?
4×6×4
=24×4
=96(dm3)
96 dm > 75.36 dm3
答:长方体的体积大。
3.14×22×6
=3.14×4×6
=12.56×6
=75.36(dm3)
5.
如图,求出小铁块的体积。
解法一:
3.14×(10÷2)2×(7-5)
=3.14×25×2
=78.5×2
=157 ( cm3 )
5cm
7cm
10cm
10cm
6.
5cm
7cm
10cm
10cm
6.
3.14×(10÷2)2×5
=3.14×25×5
=78.5×5
=392.5(cm3)
3.14×(10÷2)2×7
=3.14×25×7
=78.5×7
=549.5(cm3)
549.5-392.5=157( cm3 )
解法二:
如图,求出小铁块的体积。
奇思有一个圆柱形的水杯,水杯的底面直径是4厘米,高是10厘米,有资料显示:每人每天的正常饮水量大约是1立方分米,奇思一天要喝几杯水?
3.14×(4÷2)2×10
=12.56×10
=125.6(立方厘米)=0.1256(立方分米)
1÷0.1256≈8(杯)
答:奇思一天大约要喝8杯水。
7.
圆柱的体积是怎么计算的呢,你能写出圆柱的体积计算公式吗?
要计算一个圆柱的体积,只要用它的底面面积乘以它的高就可以了。
圆柱的体积计算公式是:
圆柱的体积=底面积×高
V=Sh
