北师大版六年级下册数学第一单元 圆柱与圆锥 整理复习课件(共36张PPT)
文档属性
| 名称 | 北师大版六年级下册数学第一单元 圆柱与圆锥 整理复习课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 06:23:39 | ||
图片预览




文档简介
(共36张PPT)
北师大版六年级数学下册
整理复习
汇报人:XXX 时间:XXXXX
一 圆柱与圆锥
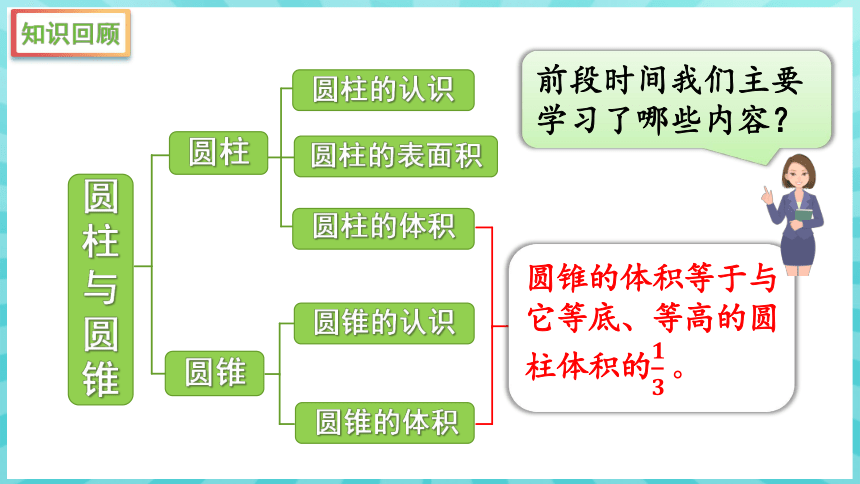
圆柱与圆锥
圆柱
圆柱的认识
圆柱的表面积
圆锥
圆柱的体积
前段时间我们主要学习了哪些内容?
圆锥的认识
圆锥的体积
圆锥的体积等于与它等底、等高的圆柱体积的
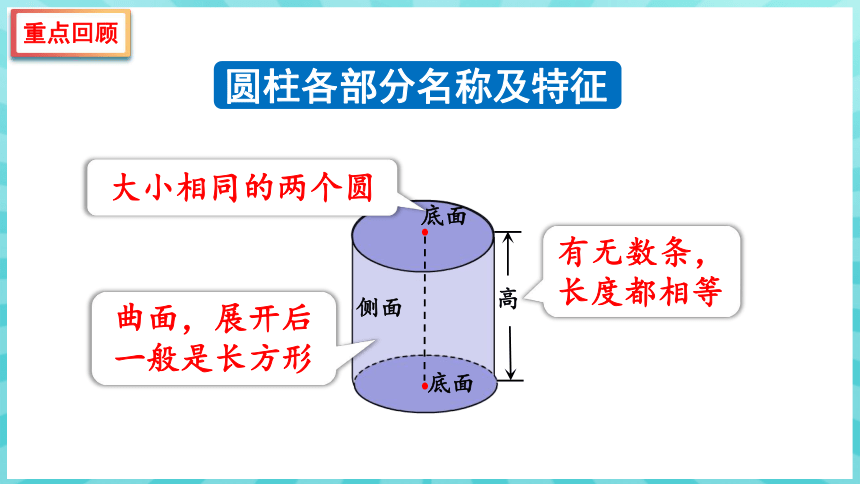
有无数条,长度都相等
侧面
底面
底面
高
大小相同的两个圆
曲面,展开后一般是长方形
圆柱各部分名称及特征
重点回顾
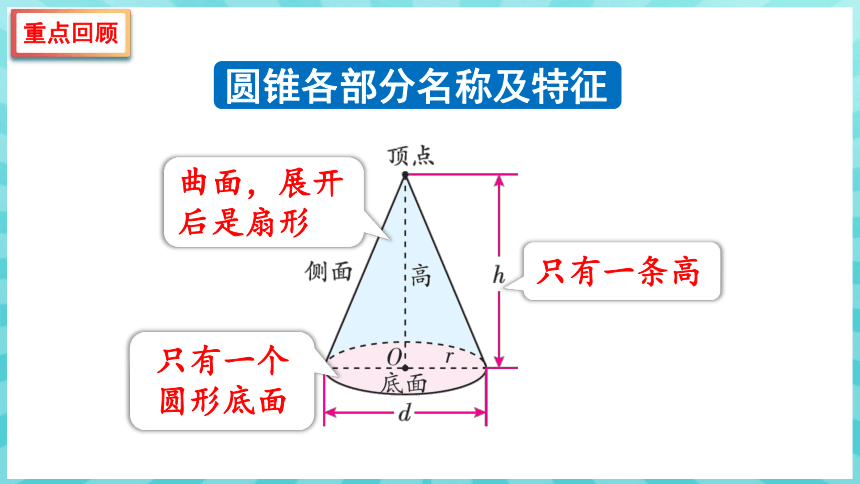
圆锥各部分名称及特征
只有一条高
只有一个圆形底面
曲面,展开后是扇形
重点回顾
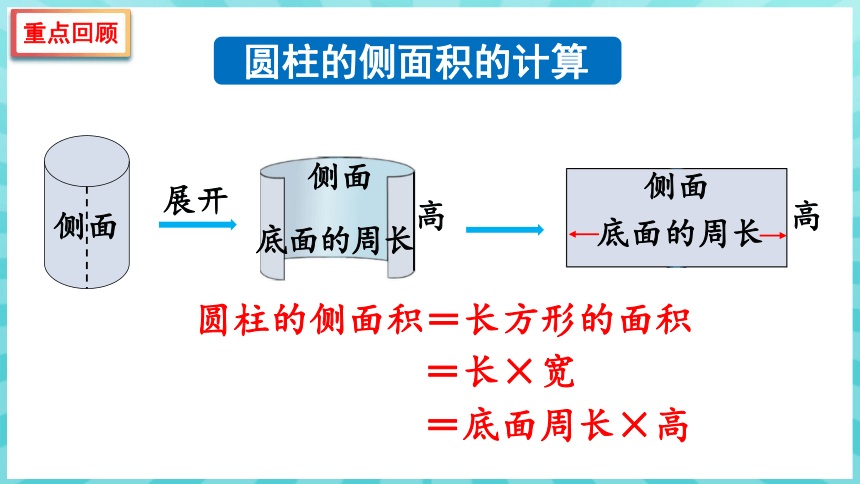
圆柱的侧面积的计算
=底面周长×高
=长×宽
圆柱的侧面积=长方形的面积
展开
侧面
底面的周长
高
底面的周长
高
侧面
侧面
重点回顾
圆柱的侧面积的计算
圆柱的侧面积=圆柱的底面周长×高
直接计算:S侧=Ch
1
利用直径计算:S侧=πdh
2
利用半径计算:S侧=2πrh
3
重点回顾
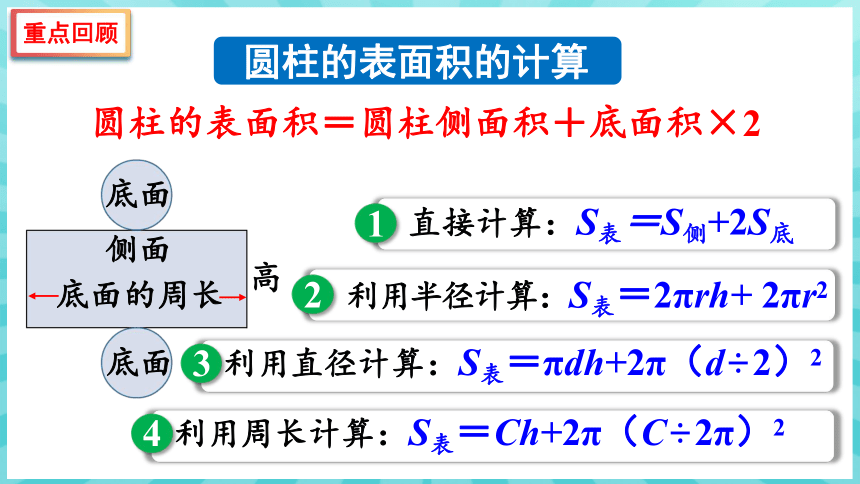
圆柱的表面积的计算
底面
底面
侧面
底面的周长
高
圆柱的表面积=圆柱侧面积+底面积×2
直接计算:S表=S侧+2S底
1
利用直径计算:S表=πdh+2π(d÷2)2
3
利用半径计算:S表=2πrh+ 2πr2
2
利用周长计算:S表=Ch+2π(C÷2π)2
4
重点回顾
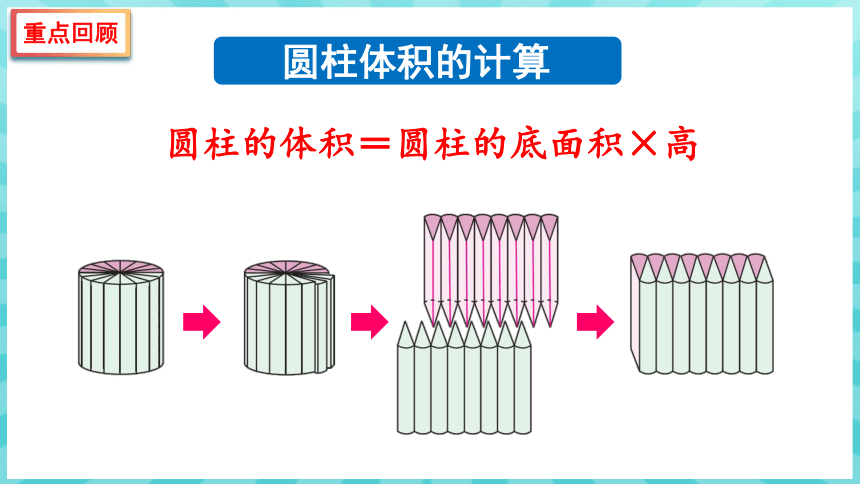
圆柱体积的计算
圆柱的体积=圆柱的底面积×高
重点回顾
圆柱体积的计算
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
1
利用直径计算:V=π(d÷2)2h
3
利用半径计算:V=πr2h
2
利用周长计算:V=π(C÷2π)2h
4
重点回顾
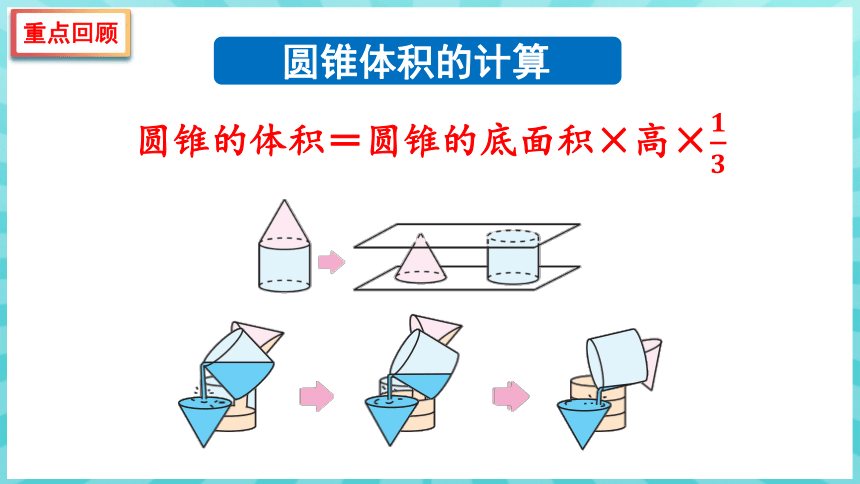
圆锥体积的计算
圆锥的体积=与它等底、等高的圆柱体积的
圆锥的体积=圆锥的底面积×高×
重点回顾
圆锥体积的计算
直接计算:V=Sh
1
利用直径计算:V=π(d÷2)2h
3
利用半径计算:V=πr2h
2
利用周长计算:V=π(C÷2π)2h
4
圆锥的体积=圆锥的底面积×高×
重点回顾
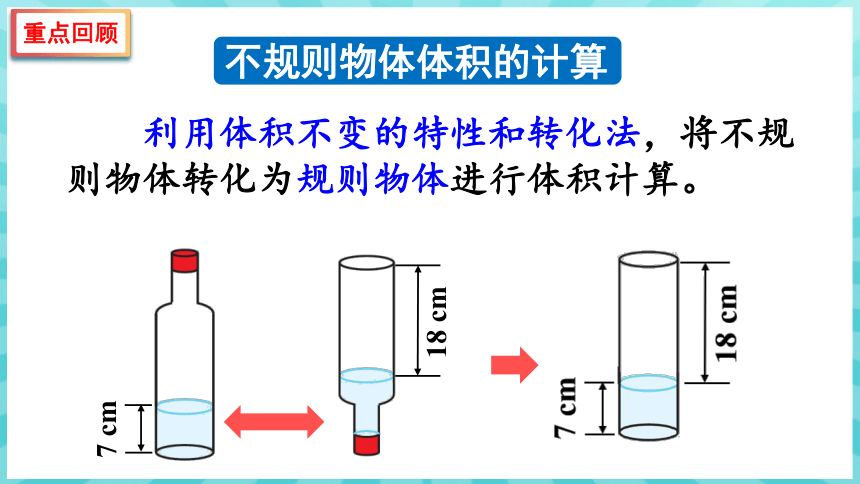
利用体积不变的特性和转化法,将不规则物体转化为规则物体进行体积计算。
不规则物体体积的计算
7 cm
18 cm
重点回顾
上面一排图形旋转后会得到下面的哪个图形?想一想,连一连。
1.
计算下面图形的体积。
3.14×32 ×6.5
=28.26×6.5
=183.69 (cm3)
3.14×(8÷2)2 ×6×
=50.24×6×
=100.48 (cm3)
2.
计算下面图形的体积。
2.
8×5 ×6.5
=40×6.5
=260 (cm3)
4×4×4
=16×4
=64(cm3)
3.
填一填。
3.5 m2=( )dm2 3400 cm2 =( )dm2
相邻两个面积单位间的进率是100。
6.5 L=( )mL 4000 mL =( )cm3 =( )dm3
2300 dm3=( ) m3 0.083m3 = ( )dm3
350
34
83
4
6500
4000
2.3
相邻两个体积、容积单位间的进率是1000。
4.
一个圆柱形城堡,底面周长是125.6 m,高是15 m。这个城堡的体积是多少立方米?
3.14×(125.6÷3.14÷2)2 ×15
=3.14×400×15
=18840(cm3)
答:这个城堡的体积是18840立方米。
(1)包装这个糖果盒的侧面,至少需要多大面积的纸?
3.14×2×7
=6.28×7
=43.96 (cm2)
答:至少需要43.96平方厘米的纸。
5.
2 cm
7 cm
(2)这个糖果盒的体积是多少?
5.
2 cm
7 cm
3.14×(2÷2) ×7
=3.14×7
=21.98(cm )
答:这个糖果盒的体积是21.98立方厘米。
油桶的表面要刷漆,每平方米需油漆 0.6 kg。每个油桶的底面直径是 40 cm,高是 60 cm,刷 100 个油桶需要多少油漆?
3.14×(40÷2)2×2
=1256×2
=2512(cm2)
3.14×40×60
=125.6×60
=7536(cm2)
6.
油桶的表面要刷漆,每平方米需油漆 0.6 kg。每个油桶的底面直径是 40 cm,高是 60 cm,刷 100 个油桶需要多少油漆?
6.
10048×100=1004800 (cm2)
100.48×0.6=60.288(kg)
答:需要60.288千克油漆。
2512+7536=10048(cm2)
1004800 cm2=100.48 m2
下面三幅图分别是什么立体图形的展开图?请在括号里填出立体图形的名称,并计算出这个立体图形的表面积。(单位:cm)
( )
( )
( )
长方体
正方体
圆柱体
7.
长方体共有6个面,相对的两个面是相等的,所以先求出上、前、左面的和,再乘2。
长方体表面积:
(50×30+50 ×15+30 ×15)×2
=(1500+750+450)×2
=2700 ×2
=5400(平方厘米)
正方体共有6个面,所有的面都 是相等的,所以先求出一个面的面积,再乘6。
正方体表面积:
5×5×6
=25×6
=150(平方厘米)
圆柱体的表面积是两个底面加一个侧面,两个底面是相等的两个圆,侧面展开是一个长方形。
圆柱体表面积:
3.14×(6÷2)2×2+3.14×6×10
=28.26×2+18.84×10
=56.52+188.4
=244.92(cm2)
如图, 先将甲容器注满水, 再将水倒入乙容器, 这时乙容器中的水有多高?
答:乙容器中的水高是4厘米,因为这两个容器等底等高,所以圆柱的容积是圆锥的3倍。
8.
如图,圆柱形钢柱有多高?(单位:cm,结果保留整数)
10×50×20
=500×20
=10000 (cm )
侧面积:
3.14×(20÷2)
=3.14×100
=314 (cm2)
10000÷314≈32 (cm)
答:圆柱形钢柱大约高32厘米。
9.
一个粮仓如下图, 如果每立方米粮食的质量为700 kg, 这个粮仓最多能装多少千克粮食?
3.14×(2÷2)2×0.6
= 1.884×
=0.628(m3)
10.
一个粮仓如下图, 如果每立方米粮食的质量为700 kg, 这个粮仓最多能装多少千克粮食?
10.
3.14×(2÷2)2×1.5
= 3.14×1.5
=4.71(m3)
0.628+4.71=5.338(m3 )
5.338×700=3736.6(kg)
答:这个粮仓最多能装3736.6千克粮食。
长方体、正方体和圆柱的体积都可以用 “V=Sh”计算。想一想,右面两个图形的体积也可以用“V=Sh” 计算吗?说一说你的想法。
11.
提示:可以用“切、拼”的方法,利用转化的思想,将右面的两个图形转化为长方体。
16÷3.14÷2
≈5.10÷2
=2.55(cm)
横着卷:
3.14×2.55 ×4
≈20.42×4
=81.68(cm )
将16 cm、宽 4 cm 的两张长方形纸,一张横着卷成圆柱形,另一张竖着卷成圆柱形。两个圆柱的体积一样大吗?猜一猜,再算一算。(结果保留两位小数)
12.
4÷3.14÷2
≈1.27÷2
=0.64(cm)
竖着卷:
3.14×0.64 ×16
≈1.29×16
=20.64(cm )
81.68(cm )> 20.64(cm )
答:两个圆柱的体积不一样大。
将16 cm、宽 4 cm 的两张长方形纸,一张横着卷成圆柱形,另一张竖着卷成圆柱形。两个圆柱的体积一样大吗?猜一猜,再算一算。(结果保留两位小数)
12.
(1)做这个布套至少用了多少布料?
13. 小雨的水壶有一个布套(如图)。
至少用的布料=圆柱的表面积
3.14×10×20+3.14× (10÷2)2×2
=628+157
=785(cm2)
答:至少用了785 cm2的布料。
(2)一壶水够1.5 L吗?(水壶和布套的厚度忽略不计。)
一壶水的体积=壶的容积
3.14×(10÷2)2×20=1570(cm3)
1570 cm3=1.57 L 1.57>1.5
答:一壶水够1.5 L。
13. 小雨的水壶有一个布套(如图)。
14.一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4 dm,圆柱高2 dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(1)这个进料漏斗大约能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
3.14×(4÷2)2×2 + ×3.14×(4÷2)2×4.2
=42.704(dm3)
42.704×0.65≈28(kg)
答:这个进料漏斗大约能装28 kg稻谷。
14.一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4 dm,圆柱高2 dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(2)如果稻谷的出米率是70%,一漏斗稻谷大约能磨出多少千克大米?
大米的质量=稻谷的质量×出米率
28×70%=19.6(kg)
答:一漏斗稻谷大约能磨出19.6 kg大米。
北师大版六年级数学下册
整理复习
汇报人:XXX 时间:XXXXX
一 圆柱与圆锥
圆柱与圆锥
圆柱
圆柱的认识
圆柱的表面积
圆锥
圆柱的体积
前段时间我们主要学习了哪些内容?
圆锥的认识
圆锥的体积
圆锥的体积等于与它等底、等高的圆柱体积的
有无数条,长度都相等
侧面
底面
底面
高
大小相同的两个圆
曲面,展开后一般是长方形
圆柱各部分名称及特征
重点回顾
圆锥各部分名称及特征
只有一条高
只有一个圆形底面
曲面,展开后是扇形
重点回顾
圆柱的侧面积的计算
=底面周长×高
=长×宽
圆柱的侧面积=长方形的面积
展开
侧面
底面的周长
高
底面的周长
高
侧面
侧面
重点回顾
圆柱的侧面积的计算
圆柱的侧面积=圆柱的底面周长×高
直接计算:S侧=Ch
1
利用直径计算:S侧=πdh
2
利用半径计算:S侧=2πrh
3
重点回顾
圆柱的表面积的计算
底面
底面
侧面
底面的周长
高
圆柱的表面积=圆柱侧面积+底面积×2
直接计算:S表=S侧+2S底
1
利用直径计算:S表=πdh+2π(d÷2)2
3
利用半径计算:S表=2πrh+ 2πr2
2
利用周长计算:S表=Ch+2π(C÷2π)2
4
重点回顾
圆柱体积的计算
圆柱的体积=圆柱的底面积×高
重点回顾
圆柱体积的计算
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
1
利用直径计算:V=π(d÷2)2h
3
利用半径计算:V=πr2h
2
利用周长计算:V=π(C÷2π)2h
4
重点回顾
圆锥体积的计算
圆锥的体积=与它等底、等高的圆柱体积的
圆锥的体积=圆锥的底面积×高×
重点回顾
圆锥体积的计算
直接计算:V=Sh
1
利用直径计算:V=π(d÷2)2h
3
利用半径计算:V=πr2h
2
利用周长计算:V=π(C÷2π)2h
4
圆锥的体积=圆锥的底面积×高×
重点回顾
利用体积不变的特性和转化法,将不规则物体转化为规则物体进行体积计算。
不规则物体体积的计算
7 cm
18 cm
重点回顾
上面一排图形旋转后会得到下面的哪个图形?想一想,连一连。
1.
计算下面图形的体积。
3.14×32 ×6.5
=28.26×6.5
=183.69 (cm3)
3.14×(8÷2)2 ×6×
=50.24×6×
=100.48 (cm3)
2.
计算下面图形的体积。
2.
8×5 ×6.5
=40×6.5
=260 (cm3)
4×4×4
=16×4
=64(cm3)
3.
填一填。
3.5 m2=( )dm2 3400 cm2 =( )dm2
相邻两个面积单位间的进率是100。
6.5 L=( )mL 4000 mL =( )cm3 =( )dm3
2300 dm3=( ) m3 0.083m3 = ( )dm3
350
34
83
4
6500
4000
2.3
相邻两个体积、容积单位间的进率是1000。
4.
一个圆柱形城堡,底面周长是125.6 m,高是15 m。这个城堡的体积是多少立方米?
3.14×(125.6÷3.14÷2)2 ×15
=3.14×400×15
=18840(cm3)
答:这个城堡的体积是18840立方米。
(1)包装这个糖果盒的侧面,至少需要多大面积的纸?
3.14×2×7
=6.28×7
=43.96 (cm2)
答:至少需要43.96平方厘米的纸。
5.
2 cm
7 cm
(2)这个糖果盒的体积是多少?
5.
2 cm
7 cm
3.14×(2÷2) ×7
=3.14×7
=21.98(cm )
答:这个糖果盒的体积是21.98立方厘米。
油桶的表面要刷漆,每平方米需油漆 0.6 kg。每个油桶的底面直径是 40 cm,高是 60 cm,刷 100 个油桶需要多少油漆?
3.14×(40÷2)2×2
=1256×2
=2512(cm2)
3.14×40×60
=125.6×60
=7536(cm2)
6.
油桶的表面要刷漆,每平方米需油漆 0.6 kg。每个油桶的底面直径是 40 cm,高是 60 cm,刷 100 个油桶需要多少油漆?
6.
10048×100=1004800 (cm2)
100.48×0.6=60.288(kg)
答:需要60.288千克油漆。
2512+7536=10048(cm2)
1004800 cm2=100.48 m2
下面三幅图分别是什么立体图形的展开图?请在括号里填出立体图形的名称,并计算出这个立体图形的表面积。(单位:cm)
( )
( )
( )
长方体
正方体
圆柱体
7.
长方体共有6个面,相对的两个面是相等的,所以先求出上、前、左面的和,再乘2。
长方体表面积:
(50×30+50 ×15+30 ×15)×2
=(1500+750+450)×2
=2700 ×2
=5400(平方厘米)
正方体共有6个面,所有的面都 是相等的,所以先求出一个面的面积,再乘6。
正方体表面积:
5×5×6
=25×6
=150(平方厘米)
圆柱体的表面积是两个底面加一个侧面,两个底面是相等的两个圆,侧面展开是一个长方形。
圆柱体表面积:
3.14×(6÷2)2×2+3.14×6×10
=28.26×2+18.84×10
=56.52+188.4
=244.92(cm2)
如图, 先将甲容器注满水, 再将水倒入乙容器, 这时乙容器中的水有多高?
答:乙容器中的水高是4厘米,因为这两个容器等底等高,所以圆柱的容积是圆锥的3倍。
8.
如图,圆柱形钢柱有多高?(单位:cm,结果保留整数)
10×50×20
=500×20
=10000 (cm )
侧面积:
3.14×(20÷2)
=3.14×100
=314 (cm2)
10000÷314≈32 (cm)
答:圆柱形钢柱大约高32厘米。
9.
一个粮仓如下图, 如果每立方米粮食的质量为700 kg, 这个粮仓最多能装多少千克粮食?
3.14×(2÷2)2×0.6
= 1.884×
=0.628(m3)
10.
一个粮仓如下图, 如果每立方米粮食的质量为700 kg, 这个粮仓最多能装多少千克粮食?
10.
3.14×(2÷2)2×1.5
= 3.14×1.5
=4.71(m3)
0.628+4.71=5.338(m3 )
5.338×700=3736.6(kg)
答:这个粮仓最多能装3736.6千克粮食。
长方体、正方体和圆柱的体积都可以用 “V=Sh”计算。想一想,右面两个图形的体积也可以用“V=Sh” 计算吗?说一说你的想法。
11.
提示:可以用“切、拼”的方法,利用转化的思想,将右面的两个图形转化为长方体。
16÷3.14÷2
≈5.10÷2
=2.55(cm)
横着卷:
3.14×2.55 ×4
≈20.42×4
=81.68(cm )
将16 cm、宽 4 cm 的两张长方形纸,一张横着卷成圆柱形,另一张竖着卷成圆柱形。两个圆柱的体积一样大吗?猜一猜,再算一算。(结果保留两位小数)
12.
4÷3.14÷2
≈1.27÷2
=0.64(cm)
竖着卷:
3.14×0.64 ×16
≈1.29×16
=20.64(cm )
81.68(cm )> 20.64(cm )
答:两个圆柱的体积不一样大。
将16 cm、宽 4 cm 的两张长方形纸,一张横着卷成圆柱形,另一张竖着卷成圆柱形。两个圆柱的体积一样大吗?猜一猜,再算一算。(结果保留两位小数)
12.
(1)做这个布套至少用了多少布料?
13. 小雨的水壶有一个布套(如图)。
至少用的布料=圆柱的表面积
3.14×10×20+3.14× (10÷2)2×2
=628+157
=785(cm2)
答:至少用了785 cm2的布料。
(2)一壶水够1.5 L吗?(水壶和布套的厚度忽略不计。)
一壶水的体积=壶的容积
3.14×(10÷2)2×20=1570(cm3)
1570 cm3=1.57 L 1.57>1.5
答:一壶水够1.5 L。
13. 小雨的水壶有一个布套(如图)。
14.一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4 dm,圆柱高2 dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(1)这个进料漏斗大约能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
3.14×(4÷2)2×2 + ×3.14×(4÷2)2×4.2
=42.704(dm3)
42.704×0.65≈28(kg)
答:这个进料漏斗大约能装28 kg稻谷。
14.一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4 dm,圆柱高2 dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(2)如果稻谷的出米率是70%,一漏斗稻谷大约能磨出多少千克大米?
大米的质量=稻谷的质量×出米率
28×70%=19.6(kg)
答:一漏斗稻谷大约能磨出19.6 kg大米。
