北师大版六年级下册数学第二单元 比例 整理与复习课件(共22张PPT)
文档属性
| 名称 | 北师大版六年级下册数学第二单元 比例 整理与复习课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 06:27:10 | ||
图片预览






文档简介
(共22张PPT)
北师大版六年级数学下册
整理与复习
汇报人:XXX 时间:XXXXX
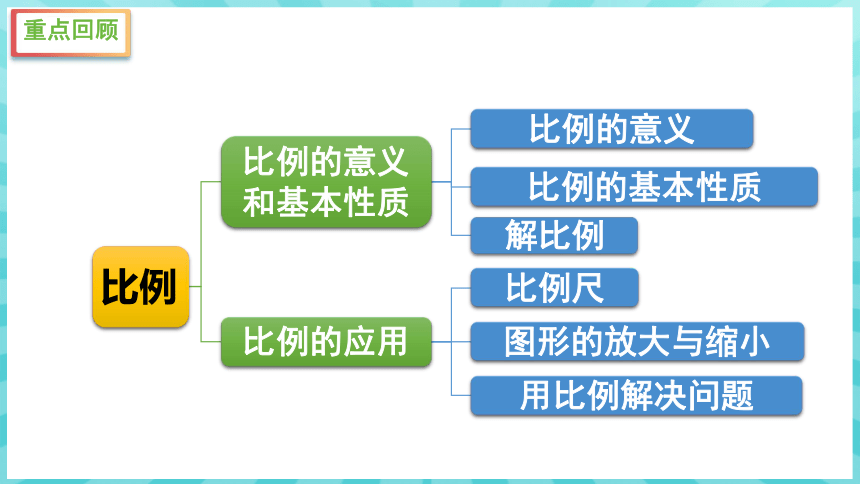
二 比例
重点回顾
比例的意义和基本性质
比例的意义:表示两个比相等的式子叫作比例。
0.6∶0.2和
∶
3
4
1
4
∶ =
3
4
1
4
3
0.6∶0.2=3
能组成比例
重点回顾
判断下面的比能否组成比例。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
比例的意义和基本性质
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
× = ×
4
1
1
2
1
6
1
3
∶ = ∶
6
1
1
2
1
3
1
4
(答案不唯一)
重点回顾
根据比例的基本性质,将算式改成比例。
解比例:根据比例的基本性质,求出比例中的未知项。
答:他的实际身高是120 cm。
比例的意义和基本性质
x∶3=40∶1
x=40×3
x=120
解:设他的实际身高是 x cm。
重点回顾
小明与他在照片中的身高比是40∶1,他在照片中的身高是3 cm,他的实际身高是多少厘米?
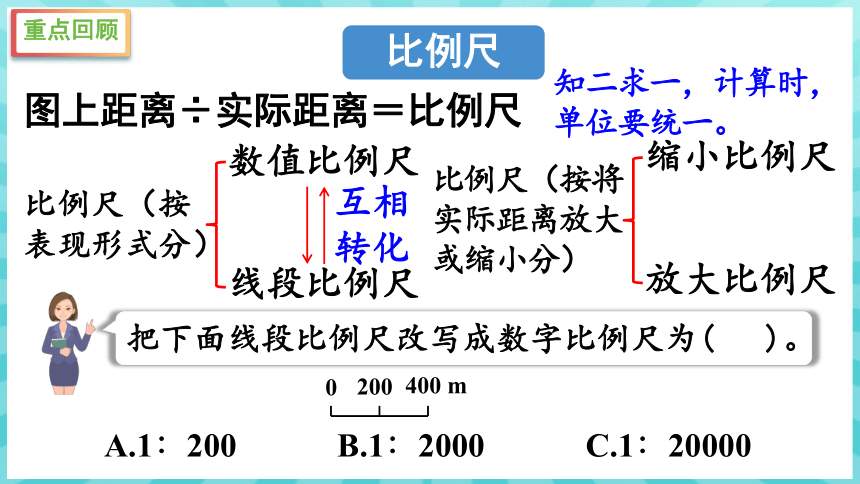
比例尺
图上距离÷实际距离=比例尺
知二求一,计算时,
单位要统一。
比例尺(按表现形式分)
数值比例尺
线段比例尺
互相
转化
A.1∶200 B.1∶2000 C.1∶20000
0
200
400 m
C
比例尺(按将实际距离放大或缩小分)
缩小比例尺
放大比例尺
重点回顾
把下面线段比例尺改写成数字比例尺为( )。
图形的放大与缩小
一数:数原图形各边各占几格。
二算:按给定的比算出图形各边放大或缩小后的长度。
三画:按算出的边长画出新图形。
形状不变,大小变。
5 cm
3 cm
5×3=15(cm)
3×3=9(cm)
15×9=135(cm2)
重点回顾
把右面的长方形按3∶1放大,得到的图形的面积是( )cm2。
135
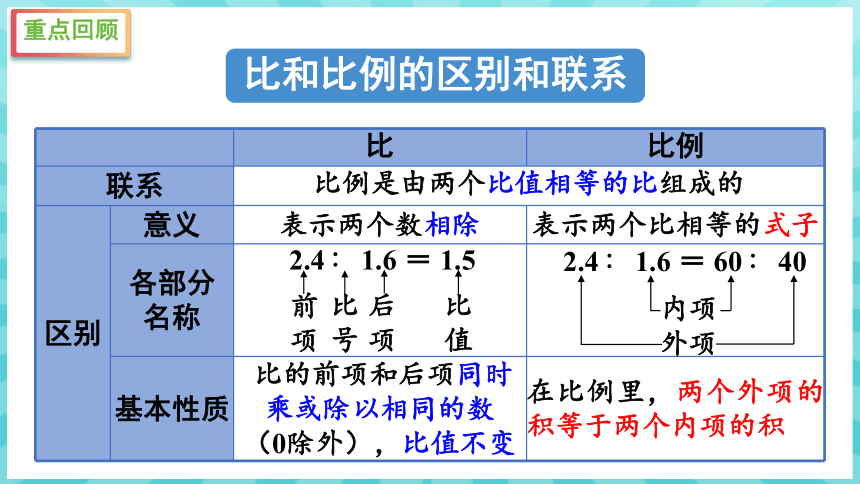
比 比例
联系 比例是由两个比值相等的比组成的
区别 意义 表示两个数相除 表示两个比相等的式子
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数 (0除外),比值不变 在比例里,两个外项的积等于两个内项的积
2.4∶1.6=1.5
前项
比号
后项
比值
2.4∶1.6=60∶40
外项
内项
比和比例的区别和联系
重点回顾
淘气把第一个三角形按比缩小, 得到第二个三角形。 你能根据图中的数据写出不同的比例吗?
5∶2.5 = 4 ∶2
5 ∶2.5 = 3 ∶1.5
4 ∶2 = 3 ∶1.5
2 ∶4 = 1.5 ∶3
2.5 ∶5 = 2 ∶4
2.5 ∶5 = 1.5 ∶3
1.
下面哪几组的两个比可以组成比例?把组成的比例写出来。
2.
解方程。
3.
淘气调制了一杯糖水, 糖与水的比是 2∶ 25, 其中糖用了 10 g, 调制这杯糖水用水多少克?
解:设调制这杯糖水用水克。
答:调制这杯糖水用水125克。
10∶ =2∶25
2 =250
=125
4.
5.
右边是某农场一个仓库的平面图。这个仓库的长是100m,宽是80m。这幅图的比例尺是多少?量一量,算一算。
6.
1∶2500
一辆汽车从 A 城开往 B 城。
(1) 比例尺 1∶ 5000000 表示什么意思?
表示图上距离1厘米代表实际距离5000000厘米或50千米。
7.
一辆汽车从 A 城开往 B 城。
(2)如果从 A 城到 B 城的图上距离是9厘米,那么实际路程是多少千米?
7.
9∶ =1∶5000000
=45000000
45000000cm=450km
解:设实际路程是厘米。
答:实际路程是450千米。
一辆汽车从 A 城开往 B 城。
(3)如果汽车平均每时行驶 60 km, 行驶 9 时能否到达 B 城。
7.
450 ÷60≈8(时)
9>8
答:行驶 9 时能到达 B 城。
中心广场四周建筑物如图所示。
(1) 医院距中心广场的图上距离是( ) cm; 已知实际距离是 200 m, 此图的比例尺是( ) 。
4
1 ∶ 5000
8.
中心广场四周建筑物如图所示。
(2)学校到图书城的图上距离是( ) cm, 实际距离是( ) m, 如果淘气每分走 50 m, 他从学校到图书城需 ( )分。
8.
9
450
9
中心广场四周建筑物如图所示。
(3)笑笑从电影院出来后经中心广场到百货商店,实际走了多少米?
8.
300
中心广场四周建筑物如图所示。
(4)游乐场在中心广场北偏东 60° 方向、 距中心广场的实际距离约 240 m,请你在图中标出游乐场所在的位置。
8.
游乐场
小红8分钟走了500米,照这样的速度,她从家里走到学校用了14分钟,小红家离学校大约多少米
解:设小红家离学校大约米。
∶14=500∶8
8 =7000
=875
答:小红家离学校大约875米。
9.
北师大版六年级数学下册
整理与复习
汇报人:XXX 时间:XXXXX
二 比例
重点回顾
比例的意义和基本性质
比例的意义:表示两个比相等的式子叫作比例。
0.6∶0.2和
∶
3
4
1
4
∶ =
3
4
1
4
3
0.6∶0.2=3
能组成比例
重点回顾
判断下面的比能否组成比例。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
比例的意义和基本性质
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
× = ×
4
1
1
2
1
6
1
3
∶ = ∶
6
1
1
2
1
3
1
4
(答案不唯一)
重点回顾
根据比例的基本性质,将算式改成比例。
解比例:根据比例的基本性质,求出比例中的未知项。
答:他的实际身高是120 cm。
比例的意义和基本性质
x∶3=40∶1
x=40×3
x=120
解:设他的实际身高是 x cm。
重点回顾
小明与他在照片中的身高比是40∶1,他在照片中的身高是3 cm,他的实际身高是多少厘米?
比例尺
图上距离÷实际距离=比例尺
知二求一,计算时,
单位要统一。
比例尺(按表现形式分)
数值比例尺
线段比例尺
互相
转化
A.1∶200 B.1∶2000 C.1∶20000
0
200
400 m
C
比例尺(按将实际距离放大或缩小分)
缩小比例尺
放大比例尺
重点回顾
把下面线段比例尺改写成数字比例尺为( )。
图形的放大与缩小
一数:数原图形各边各占几格。
二算:按给定的比算出图形各边放大或缩小后的长度。
三画:按算出的边长画出新图形。
形状不变,大小变。
5 cm
3 cm
5×3=15(cm)
3×3=9(cm)
15×9=135(cm2)
重点回顾
把右面的长方形按3∶1放大,得到的图形的面积是( )cm2。
135
比 比例
联系 比例是由两个比值相等的比组成的
区别 意义 表示两个数相除 表示两个比相等的式子
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数 (0除外),比值不变 在比例里,两个外项的积等于两个内项的积
2.4∶1.6=1.5
前项
比号
后项
比值
2.4∶1.6=60∶40
外项
内项
比和比例的区别和联系
重点回顾
淘气把第一个三角形按比缩小, 得到第二个三角形。 你能根据图中的数据写出不同的比例吗?
5∶2.5 = 4 ∶2
5 ∶2.5 = 3 ∶1.5
4 ∶2 = 3 ∶1.5
2 ∶4 = 1.5 ∶3
2.5 ∶5 = 2 ∶4
2.5 ∶5 = 1.5 ∶3
1.
下面哪几组的两个比可以组成比例?把组成的比例写出来。
2.
解方程。
3.
淘气调制了一杯糖水, 糖与水的比是 2∶ 25, 其中糖用了 10 g, 调制这杯糖水用水多少克?
解:设调制这杯糖水用水克。
答:调制这杯糖水用水125克。
10∶ =2∶25
2 =250
=125
4.
5.
右边是某农场一个仓库的平面图。这个仓库的长是100m,宽是80m。这幅图的比例尺是多少?量一量,算一算。
6.
1∶2500
一辆汽车从 A 城开往 B 城。
(1) 比例尺 1∶ 5000000 表示什么意思?
表示图上距离1厘米代表实际距离5000000厘米或50千米。
7.
一辆汽车从 A 城开往 B 城。
(2)如果从 A 城到 B 城的图上距离是9厘米,那么实际路程是多少千米?
7.
9∶ =1∶5000000
=45000000
45000000cm=450km
解:设实际路程是厘米。
答:实际路程是450千米。
一辆汽车从 A 城开往 B 城。
(3)如果汽车平均每时行驶 60 km, 行驶 9 时能否到达 B 城。
7.
450 ÷60≈8(时)
9>8
答:行驶 9 时能到达 B 城。
中心广场四周建筑物如图所示。
(1) 医院距中心广场的图上距离是( ) cm; 已知实际距离是 200 m, 此图的比例尺是( ) 。
4
1 ∶ 5000
8.
中心广场四周建筑物如图所示。
(2)学校到图书城的图上距离是( ) cm, 实际距离是( ) m, 如果淘气每分走 50 m, 他从学校到图书城需 ( )分。
8.
9
450
9
中心广场四周建筑物如图所示。
(3)笑笑从电影院出来后经中心广场到百货商店,实际走了多少米?
8.
300
中心广场四周建筑物如图所示。
(4)游乐场在中心广场北偏东 60° 方向、 距中心广场的实际距离约 240 m,请你在图中标出游乐场所在的位置。
8.
游乐场
小红8分钟走了500米,照这样的速度,她从家里走到学校用了14分钟,小红家离学校大约多少米
解:设小红家离学校大约米。
∶14=500∶8
8 =7000
=875
答:小红家离学校大约875米。
9.
