苏教版六年级下册数学总复习 图形与几何 图形的运动课件(共36张PPT)
文档属性
| 名称 | 苏教版六年级下册数学总复习 图形与几何 图形的运动课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 07:04:35 | ||
图片预览






文档简介
(共36张PPT)
总复习
图形的运动
七
2.图形与几何
图形的运动
轴对称
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
平移旋转
图形的放大与缩小
画平移和旋转后的图形
画放大或缩小后的图形
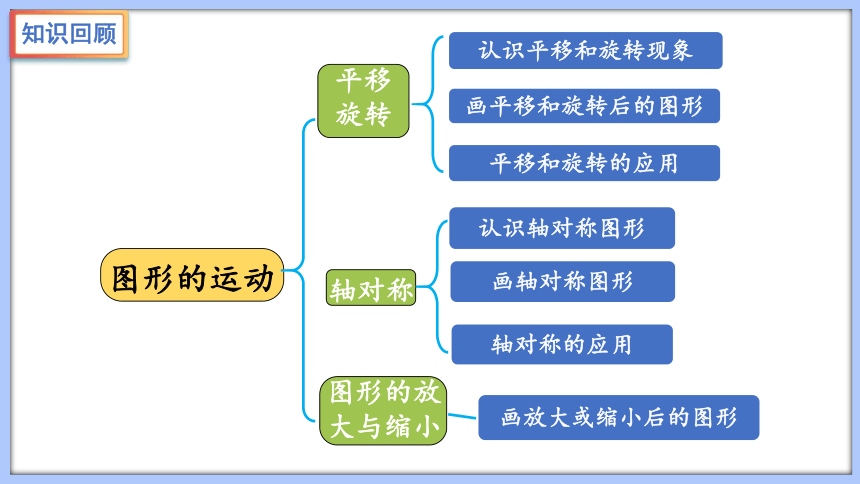
知识回顾
(教材第97页)
图形的运动有哪些?
平移
旋转
放大
缩小
轴对称
通过平移、旋转,可以改变图形的位置而不改变图形的形状和大小。
把图形的按比例放大或缩小,图形的大小改变,而图形的形状不会改变。
怎样只改变图形的位置而不改变图形的形状和大小?
怎样只改变图形的大小而不改变图形的形状?
图形的平移 意义
要素
特点
画法
在同一平面内,将一个图形沿一直线移动一定的距离,这样的图形运动叫作平移。
平移的方向、平移的距离。
只改变图形的位置,不改变图形的形状、大小及方向。
先找出图形的关键点,再按要求平移相应的距离,最后把这些点顺次连接起来。
图形的旋转 意义
要素
特点
画法
在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的图形运动叫作旋转。
旋转中心、旋转方向、旋转角度。
图形的位置、方向都改变了,但形状和大小都不变。
先找准旋转中心,然后确定旋转的方向和旋转的角度,再分别旋转各边,最后画出各边的对应边。
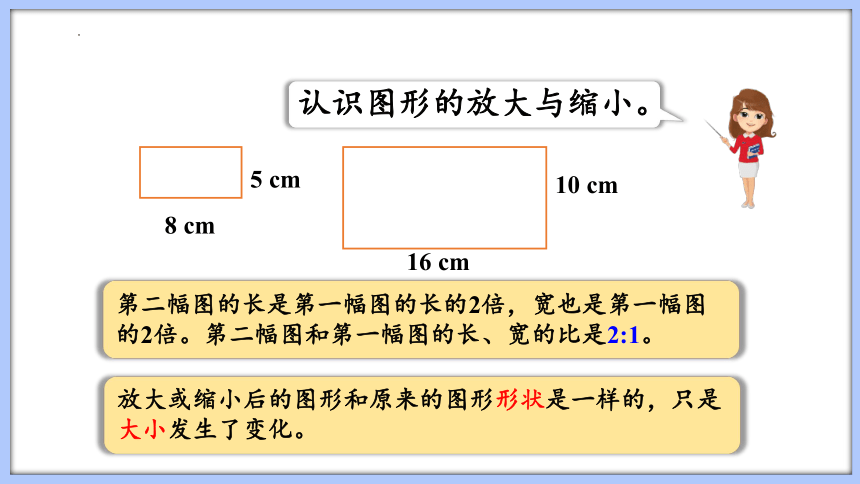
放大或缩小后的图形和原来的图形形状是一样的,只是大小发生了变化。
8 cm
5 cm
16 cm
10 cm
第二幅图的长是第一幅图的长的2倍,宽也是第一幅图的2倍。第二幅图和第一幅图的长、宽的比是2:1。
认识图形的放大与缩小。
将一个图形按一定的比放大或缩小,原图形与新图形的各边长之比和周长之比等于这个比,而它们的面积之比等于这个比的平方。
把一个图形的各边按一定的比进行放大或缩小,从而得到该图形的放大图形或缩小图形。
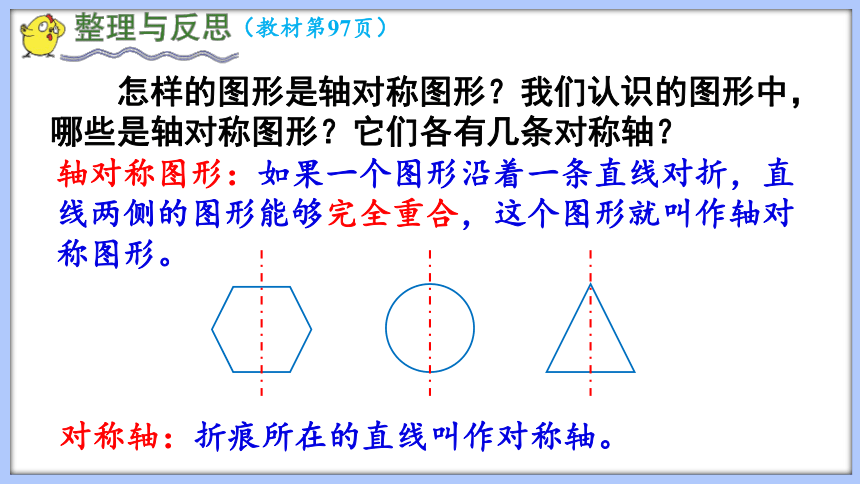
(教材第97页)
怎样的图形是轴对称图形?我们认识的图形中,哪些是轴对称图形?它们各有几条对称轴?
轴对称图形:如果一个图形沿着一条直线对折,直线两侧的图形能够完全重合,这个图形就叫作轴对称图形。
对称轴:折痕所在的直线叫作对称轴。
( )条
对称轴
( )条
对称轴
2
( )条
对称轴
无数
( )条
对称轴
0
5
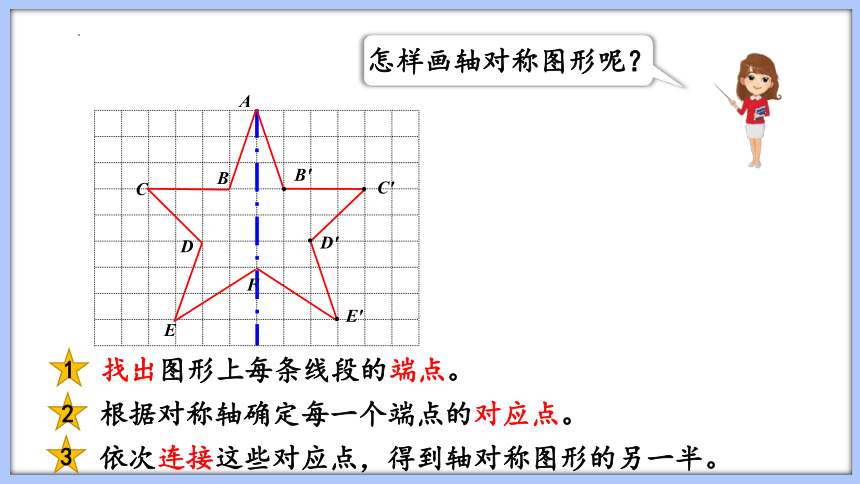
怎样画轴对称图形呢?
找出图形上每条线段的端点。
B
C
D
B′
C′
D′
E′
E
F
A
1
根据对称轴确定每一个端点的对应点。
2
依次连接这些对应点,得到轴对称图形的另一半。
3
·
·
·
·
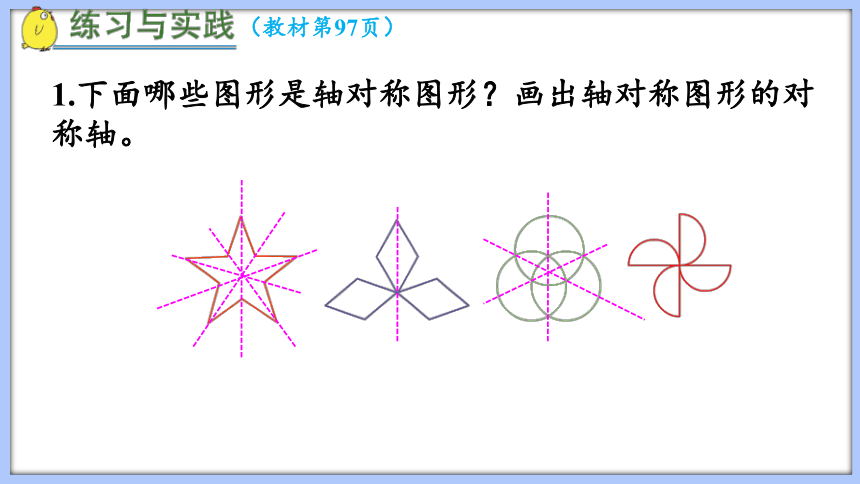
1.下面哪些图形是轴对称图形?画出轴对称图形的对称轴。
(教材第97页)
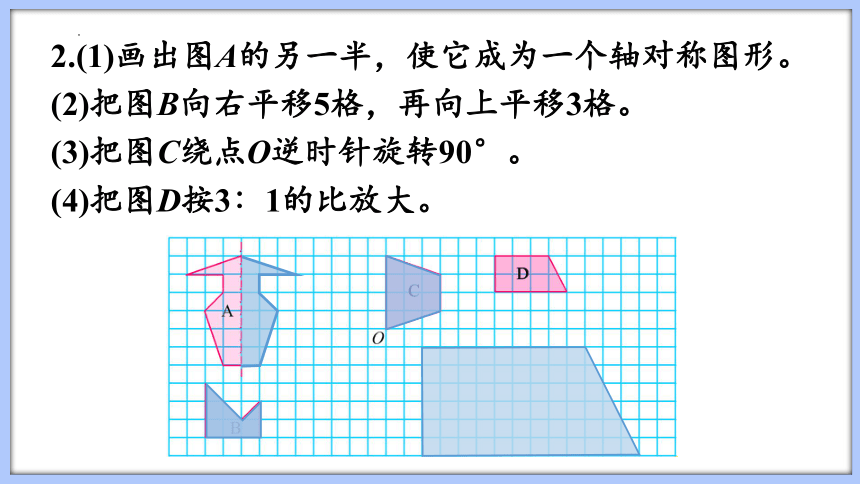
2.(1)画出图A的另一半,使它成为一个轴对称图形。
(2)把图B向右平移5格,再向上平移3格。
(3)把图C绕点О逆时针旋转90°。
(4)把图D按3∶1的比放大。
3.把左边的圆平移,使平移后的圆与右边的线段组成轴对称图形。
(1)圆应向什么方向平移几格?
(2)你能画出组成的轴对称图形的对称轴吗?
(3)对称轴通过圆心吗?它与已知线段有什么关系?
对称轴通过圆心,它与已知线段互相垂直。
4.按1∶2的比画出三角形缩小后的图形。
2×4÷2=4
4×8÷2=16
4∶16=1∶4
答:新图形与原来的图形面积的比是1∶4。
5.从左边四种瓷砖中选择两种,可以拼成不同的图案(如下图)。
②④
①③
(1)这两个图案各选择了哪几种瓷砖?
(2)任意选择两种瓷砖,设计几种不同的图案,与同学交流。
剪两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积有没有变化?你能说明自己的想法吗?
重叠部分的面积没有变化,因为无论如何旋转形成的图形都可以拼接成正方形的 。
(1)风车转动是( )现象,推拉窗户是( )现象。(填“平移”或“旋转”)
旋转
平移
沿直线移动一定的距离。
1.填一填。
绕中心点逆时针转动360°。
巩固练习
(2)把一个边长为10厘米的正方形按3∶1放大,放大后所得图形的面积是( )平方厘米。
900
可以先求出放大后的边长再求放大后的面积;也可以先求出放大前的面积再求放大后的面积。
方法一:(10×3)2=900(cm2)
方法二:10×10×32=900(cm2)
(3)一个底面直径是4厘米、高是3厘米的圆柱,放大后底面的周长是62.8厘米,这个圆柱是按( )放大了,放大后的圆柱的底面积是( )平方厘米。
5∶1
314
放大后的底面直径:62.8÷3.14=20(cm)
放大后与放大前的比:20∶4=5∶1
放大后的底面积:3.14×(20÷2)2=314(cm2)
(1)下面物体的运动方式中,( )与其他三种运动方式不同。
A.螺旋桨的运动
B.抽屉的拉动
C.风扇叶片的转动
D.钟摆的摆动
B
旋转
平移
旋转
旋转
2.选一选。
(2)将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,然后剪下一个角,如下图所示。将这张纸片展开后应该是( )。
B
A
B
C
D
(3)下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形
B.梯形
C.圆
D.平行四边形
C
旋转、平移
旋转、平移
剪拼
割补、平移
3.如图,直角三角形ABC中的空白部分是正方形,正方形的一个顶点D将这个直角三角形的斜边分成两部分,已知AD=4 cm,CD=6 cm,求阴影部分的面积。
F
E
D
C
B
A
4 cm
6 cm
将三角形ADF绕D点逆时针旋转90°。
阴影部分就转化成了一个两条直角边分别是4 cm和6 cm的直角三角形。
4×6÷2=12(cm2)
答:阴影部分的面积是12 cm2。
4 cm
4.操作题。
(1)将图中A图形先向( )平移( )格,再向( )平移( )格,就能和B图形拼成一个正方形。
O
·
A
B
右 4
下 2
右 4
下 2
4.操作题。
(2)在图中画出B图形绕点O逆时针旋转90°后的图形。
O
·
A
B
B
(3)按2∶1的比画出B图形放大后的图形。
5.你能画出下面轴对称图形的另一半吗?
·
·
·
·
·
·
·
·
·
·
·
·
先找出已知图形的几个关键点,在对称轴的另一侧找出它们的对应点,按已知图形形状连接各对应点,就画出了轴对称图形的另一半。
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
如果再涂一个小正方形后阴影部分能组成轴对称图形,那么原先的三个小正方形里必有两个小正方形关于这条对称轴对称。因此,我们从其中两个小正方形能画出的对称轴着手考虑。
拓展提升
1
2
3
首先找出正方形1和2的对称轴。
涂法一
涂法二
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
再找出正方形2和3的对称轴。
与涂法二重复
涂法三
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
找出正方形1和3的对称轴。
涂法五
涂法四
其余几种情况与之前的重复
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
有5种不同的涂法
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
2.如图,下面的方格图中有4个三角形,把红色三角形向右平移2格,黄色和蓝色三角形分别向上平移2格,绿色三角形向左平移2格,这4个三角形会组成一个什么样的图案?
组成了美丽的风车。你也会像这样利用平移和旋转的知识设计有趣的图形问题吗?
3.找规律画图形。
(1)
先观察其中一个小图形的位置,如蓝色三角形依次出现在左、上、右的位置,由此猜测每一幅图可能是由前一幅图绕中心点顺时针旋转90°形成的,然后再观察验证。
3.找规律画图形。
(2)
图中的三角形依次出现在左下、右下、右上的位置,由此猜测每一幅图可能是由前一幅图绕中心点顺时针旋转90°形成的,然后再观察验证。
4.先画出一个周长是6.28 cm的圆,再画出把这个圆按3∶2放大后的圆,使得这两个圆组成一个有无数条对称轴的图形,并画出两条互相垂直的对称轴。
6.28÷3.14÷2=1(cm)
1÷2×3=1.5(cm)
两个圆的半径分别是1 cm、1.5 cm。
半径=周长÷3.14÷2
1cm
1.5 cm
互相垂直的对称轴有无数组。
4.先画出一个周长是6.28 cm的圆,再画出把这个圆按3∶2放大后的圆,使得这两个圆组成一个有无数条对称轴的图形,并画出两条互相垂直的对称轴。
同心圆有无数条对称轴。
总复习
图形的运动
七
2.图形与几何
图形的运动
轴对称
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
平移旋转
图形的放大与缩小
画平移和旋转后的图形
画放大或缩小后的图形
知识回顾
(教材第97页)
图形的运动有哪些?
平移
旋转
放大
缩小
轴对称
通过平移、旋转,可以改变图形的位置而不改变图形的形状和大小。
把图形的按比例放大或缩小,图形的大小改变,而图形的形状不会改变。
怎样只改变图形的位置而不改变图形的形状和大小?
怎样只改变图形的大小而不改变图形的形状?
图形的平移 意义
要素
特点
画法
在同一平面内,将一个图形沿一直线移动一定的距离,这样的图形运动叫作平移。
平移的方向、平移的距离。
只改变图形的位置,不改变图形的形状、大小及方向。
先找出图形的关键点,再按要求平移相应的距离,最后把这些点顺次连接起来。
图形的旋转 意义
要素
特点
画法
在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的图形运动叫作旋转。
旋转中心、旋转方向、旋转角度。
图形的位置、方向都改变了,但形状和大小都不变。
先找准旋转中心,然后确定旋转的方向和旋转的角度,再分别旋转各边,最后画出各边的对应边。
放大或缩小后的图形和原来的图形形状是一样的,只是大小发生了变化。
8 cm
5 cm
16 cm
10 cm
第二幅图的长是第一幅图的长的2倍,宽也是第一幅图的2倍。第二幅图和第一幅图的长、宽的比是2:1。
认识图形的放大与缩小。
将一个图形按一定的比放大或缩小,原图形与新图形的各边长之比和周长之比等于这个比,而它们的面积之比等于这个比的平方。
把一个图形的各边按一定的比进行放大或缩小,从而得到该图形的放大图形或缩小图形。
(教材第97页)
怎样的图形是轴对称图形?我们认识的图形中,哪些是轴对称图形?它们各有几条对称轴?
轴对称图形:如果一个图形沿着一条直线对折,直线两侧的图形能够完全重合,这个图形就叫作轴对称图形。
对称轴:折痕所在的直线叫作对称轴。
( )条
对称轴
( )条
对称轴
2
( )条
对称轴
无数
( )条
对称轴
0
5
怎样画轴对称图形呢?
找出图形上每条线段的端点。
B
C
D
B′
C′
D′
E′
E
F
A
1
根据对称轴确定每一个端点的对应点。
2
依次连接这些对应点,得到轴对称图形的另一半。
3
·
·
·
·
1.下面哪些图形是轴对称图形?画出轴对称图形的对称轴。
(教材第97页)
2.(1)画出图A的另一半,使它成为一个轴对称图形。
(2)把图B向右平移5格,再向上平移3格。
(3)把图C绕点О逆时针旋转90°。
(4)把图D按3∶1的比放大。
3.把左边的圆平移,使平移后的圆与右边的线段组成轴对称图形。
(1)圆应向什么方向平移几格?
(2)你能画出组成的轴对称图形的对称轴吗?
(3)对称轴通过圆心吗?它与已知线段有什么关系?
对称轴通过圆心,它与已知线段互相垂直。
4.按1∶2的比画出三角形缩小后的图形。
2×4÷2=4
4×8÷2=16
4∶16=1∶4
答:新图形与原来的图形面积的比是1∶4。
5.从左边四种瓷砖中选择两种,可以拼成不同的图案(如下图)。
②④
①③
(1)这两个图案各选择了哪几种瓷砖?
(2)任意选择两种瓷砖,设计几种不同的图案,与同学交流。
剪两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积有没有变化?你能说明自己的想法吗?
重叠部分的面积没有变化,因为无论如何旋转形成的图形都可以拼接成正方形的 。
(1)风车转动是( )现象,推拉窗户是( )现象。(填“平移”或“旋转”)
旋转
平移
沿直线移动一定的距离。
1.填一填。
绕中心点逆时针转动360°。
巩固练习
(2)把一个边长为10厘米的正方形按3∶1放大,放大后所得图形的面积是( )平方厘米。
900
可以先求出放大后的边长再求放大后的面积;也可以先求出放大前的面积再求放大后的面积。
方法一:(10×3)2=900(cm2)
方法二:10×10×32=900(cm2)
(3)一个底面直径是4厘米、高是3厘米的圆柱,放大后底面的周长是62.8厘米,这个圆柱是按( )放大了,放大后的圆柱的底面积是( )平方厘米。
5∶1
314
放大后的底面直径:62.8÷3.14=20(cm)
放大后与放大前的比:20∶4=5∶1
放大后的底面积:3.14×(20÷2)2=314(cm2)
(1)下面物体的运动方式中,( )与其他三种运动方式不同。
A.螺旋桨的运动
B.抽屉的拉动
C.风扇叶片的转动
D.钟摆的摆动
B
旋转
平移
旋转
旋转
2.选一选。
(2)将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,然后剪下一个角,如下图所示。将这张纸片展开后应该是( )。
B
A
B
C
D
(3)下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形
B.梯形
C.圆
D.平行四边形
C
旋转、平移
旋转、平移
剪拼
割补、平移
3.如图,直角三角形ABC中的空白部分是正方形,正方形的一个顶点D将这个直角三角形的斜边分成两部分,已知AD=4 cm,CD=6 cm,求阴影部分的面积。
F
E
D
C
B
A
4 cm
6 cm
将三角形ADF绕D点逆时针旋转90°。
阴影部分就转化成了一个两条直角边分别是4 cm和6 cm的直角三角形。
4×6÷2=12(cm2)
答:阴影部分的面积是12 cm2。
4 cm
4.操作题。
(1)将图中A图形先向( )平移( )格,再向( )平移( )格,就能和B图形拼成一个正方形。
O
·
A
B
右 4
下 2
右 4
下 2
4.操作题。
(2)在图中画出B图形绕点O逆时针旋转90°后的图形。
O
·
A
B
B
(3)按2∶1的比画出B图形放大后的图形。
5.你能画出下面轴对称图形的另一半吗?
·
·
·
·
·
·
·
·
·
·
·
·
先找出已知图形的几个关键点,在对称轴的另一侧找出它们的对应点,按已知图形形状连接各对应点,就画出了轴对称图形的另一半。
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
如果再涂一个小正方形后阴影部分能组成轴对称图形,那么原先的三个小正方形里必有两个小正方形关于这条对称轴对称。因此,我们从其中两个小正方形能画出的对称轴着手考虑。
拓展提升
1
2
3
首先找出正方形1和2的对称轴。
涂法一
涂法二
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
再找出正方形2和3的对称轴。
与涂法二重复
涂法三
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
找出正方形1和3的对称轴。
涂法五
涂法四
其余几种情况与之前的重复
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
1
2
3
有5种不同的涂法
1.图中已有三个三个小正方形涂上阴影,若再从其他小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,有几种不同的涂法?画一画。
2.如图,下面的方格图中有4个三角形,把红色三角形向右平移2格,黄色和蓝色三角形分别向上平移2格,绿色三角形向左平移2格,这4个三角形会组成一个什么样的图案?
组成了美丽的风车。你也会像这样利用平移和旋转的知识设计有趣的图形问题吗?
3.找规律画图形。
(1)
先观察其中一个小图形的位置,如蓝色三角形依次出现在左、上、右的位置,由此猜测每一幅图可能是由前一幅图绕中心点顺时针旋转90°形成的,然后再观察验证。
3.找规律画图形。
(2)
图中的三角形依次出现在左下、右下、右上的位置,由此猜测每一幅图可能是由前一幅图绕中心点顺时针旋转90°形成的,然后再观察验证。
4.先画出一个周长是6.28 cm的圆,再画出把这个圆按3∶2放大后的圆,使得这两个圆组成一个有无数条对称轴的图形,并画出两条互相垂直的对称轴。
6.28÷3.14÷2=1(cm)
1÷2×3=1.5(cm)
两个圆的半径分别是1 cm、1.5 cm。
半径=周长÷3.14÷2
1cm
1.5 cm
互相垂直的对称轴有无数组。
4.先画出一个周长是6.28 cm的圆,再画出把这个圆按3∶2放大后的圆,使得这两个圆组成一个有无数条对称轴的图形,并画出两条互相垂直的对称轴。
同心圆有无数条对称轴。
