苏教版六年级下册数学总复习 图形与几何 图形与位置课件(共36张PPT)
文档属性
| 名称 | 苏教版六年级下册数学总复习 图形与几何 图形与位置课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 07:05:32 | ||
图片预览










文档简介
(共36张PPT)
总复习
图形与位置
七
2.图形与几何
(教材第99页)
我们学过哪些确定位置的方法?
在确定位置时,还应用过哪些知识?
还可以用数对
来表示位置。
用东、南、西、北 表示物体之间的位 置关系。
用上、下、前、后、左、右确定位置。
可以用方向和距离 确定位置。
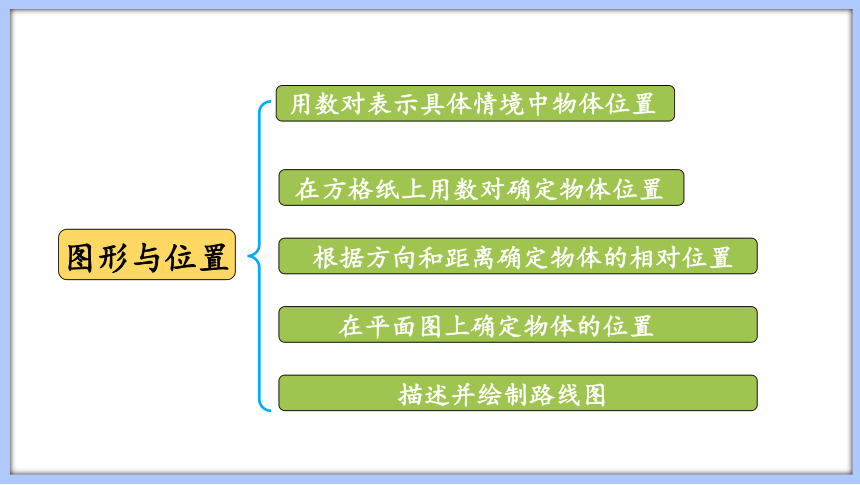
图形与位置
用数对表示具体情境中物体位置
在方格纸上用数对确定物体位置
根据方向和距离确定物体的相对位置
描述并绘制路线图
在平面图上确定物体的位置
用数对表示物体的位置
先列(竖排)后行(横排),用小括号把列数和行数相对应的数字括起来,并用逗号隔开,即(列数,行数)。
竖排叫作列,横排叫作行。确定第几列一般
从左往右数,确定第几行一般从前往后数。
用数对确定物体的位置。
如果第一个数字相同,则表示在同一列;
如果第二个数字相同,则表示在同一行。
(a ,b)
列数
行数
用方向和距离确定物体的位置
确定观测点,画出方向标。
把观测点和观察目标连起来,与南北方向形成一个角,测量出该角的度数。
用方向和距离确定物体的位置
测量出观测点和观测目标的图上距离,根据比例尺与图上距离计算出实际距离。
根据方向和距离两个条件就能精确地确定平面内物体的位置。
两种确定位置的方法有怎样的联系和区别
用数对确定位置,一定要先说列,再说行。
用方向和距离确定位置时,一定要先找准物体或地点所在的方向区域,一般先说夹角的方向。
两种确定位置的方式都要先确定标准,位置具有相对性。
描述行走路线
描述行走路线时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所行走的方向和距离,即每一步都要说清起点在哪,沿着什么方向走了多远的路程,终点在哪。
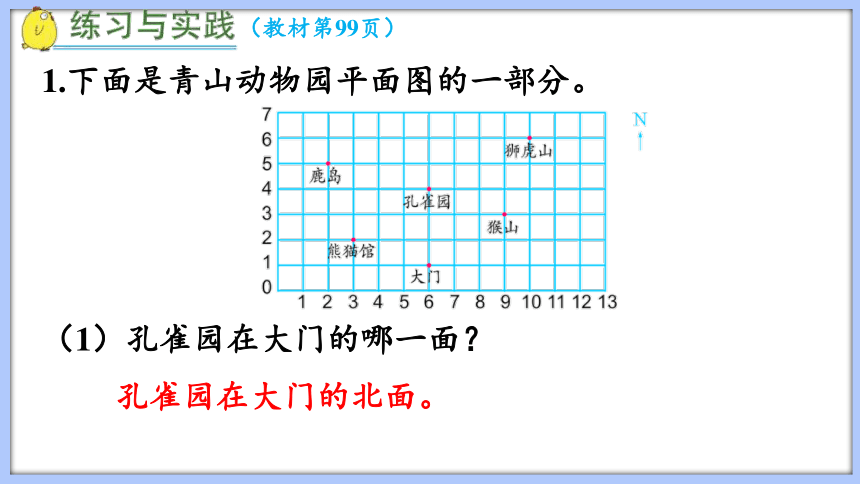
(1)孔雀园在大门的哪一面?
1.下面是青山动物园平面图的一部分。
孔雀园在大门的北面。
(教材第99页)
1.下面是青山动物园平面图的一部分。
(2)猴山在孔雀园的哪一面?狮虎山、鹿岛和熊猫馆呢?
猴山在孔雀园的东南面,狮虎山在孔雀园的东北面,鹿岛在孔雀园的西北面,熊猫馆在孔雀园的西南面。
(3)小华设计了一条游览路线,并用如下方法表示:
(6,1)→(9,3)→(10,6)→(6,4)→(2,5)→(3,2)→(6,1)
先按顺序说说小华游览的景点,再设计一条不同的游览路线,与同学交流。
小华从大门(6,1)→ 猴山(9,3)→ 狮虎山(10,6)→孔雀园(6,4)→ 鹿岛(2,5)→ 熊猫馆(3,2)→ 大门(6,1)
(路线不唯一)
2.以电视塔为观测点、填一填,画一画。
(1)市民广场在电视塔( )方向( )米处,电信大楼在电视塔( )方向( )米处。
正东
160
240
正北
2.以电视塔为观测点、填一填,画一画。
(2)市政府在电视塔( )偏( )( )°方向( )米处,少年宫在电视塔( )偏( )( )°方向( )米处。
北
50
东
320
南
35
西
240
2.以电视塔为观测点、填一填,画一画。
(3)百货大楼在电视塔南偏东30°方向240米处,图书馆在电视塔北偏西45°方向320米处。在图中表示出百货大楼和图书馆的位置。
3.下面是2路公共汽车行驶的路线图。说一说从红梅新村到淮定桥的行驶方向和经过的站点。
2路公共汽车从红梅新村出发,先向北行驶到东园,再向北偏西方向行驶到兴民巷,再向西行驶到青年路,再向南偏西方向行驶到时代广场,再向西先后行驶到电子城和科技大厦,再向南行驶到城中公园,再向北偏西方向行驶到钟楼,再向西行驶到西门,最后向北行驶到淮定桥。
4.你的家乡在哪里?有哪些旅游景点?小组合作,一部分同学扮演外地客人,其他同学试着介绍家乡的位置、旅游景点,以及游览路线。
1.(1)在下面的方格图中画出一个三角形,三个顶点分别为A(1,6)、B(1,3)、C(3,3),这个三角形是( )三角形。
123456789
10 11 12 13 14 15
76543210
直角
·A
·B
·
C
巩固练习
(2)画出这个三角形先向下平移2格,再向右平移6格后的图形,并用数对标出三个顶点的位置。
123456789
10 11 12 13 14 15
76543210
·A
·B
·
C
(7,4)
(7,1)
(9,1)
位置发生变化,表示的数对也发生变化。
76543210
(3)每个小方格的边长表示1 cm,以AB所在的直线为轴将三角形ABC旋转一周,将得到一个( ),它的体积是( )cm3。
123456789
10 11 12 13 14 15
·A
·B
·
C
(7,4)
(7,1)
(9,1)
圆锥
圆锥的底面半径是2 cm,高是3 cm。
3.14×22×3÷3=12.56(cm3)
12.56
2.如下图,以电视塔为观测点,填一填。
(1)市民广场在电视塔的( )方向( )米处。
正东
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
(2)电信大楼在电视塔的( )偏( )( )°方向( )米处。
160
(3)少年宫在电视塔的( )偏( )( )°方向( )米处。
北
40
东
240
南
30
西
240
电信业务,她首先要从市民广场往( )方向步行( )米到达电视塔,再往( )偏( )( )°方向行( )米即可到达。
正西
(2)王阿姨的家住在市民广场附近,一天早晨,她打算从市民广场出发,步行经过电视塔去电信大楼办理
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
160
北
40
东
240
·
从“市民广场”出发时观测点是“市民广场”。
从“电视塔”出发时观测点是“电视塔”。
0
9
3.如下图,平行四边形ABCD的三个顶点A、B、C的位置用数对表示分别是(4,6)、(1,3)、(5,3),那么顶点D的位置用数对表示为( )。
8,6
4
6
1
3
5
2
3
8
6
7
4格
1
2
4
5
7
D
C
B
A
4格
根据已知的三个顶点的数对画出带刻度的方格纸,就可以用数对表示出D点的位置。
4.下面是某地12路公交车的行驶路线图。
(1)12路公交车从游乐园出发,向( )方向行1.5 km到达邮局,再向( )偏( )( )°方向行( )km到达医院。
正东
北
游乐园
邮局
医院
1km
超市
电影院
书店
1.8km
2.5km
40°
60°
70°
北
东
40
2
2km
1.5km
4.下面是某地12路公交车的行驶路线图。
(2)从超市向( )偏( )( )°方向行( )km到达电影院,再向( )偏( )( )°方向行( )km到达书店。
北
游乐园
1.5km
邮局
2km
医院
超市
电影院
书店
1.8km
2.5km
40°
60°
70°
南
东
60
1.8
北
东
70
2.5
1km
1.在方格纸上画一个长方形,其中三个顶点的位置分别是(3,4),(8,4),(3,6),那么第四个顶点的位置是( , )。
A( , )
3
6
B( , )
3
4
D( , )
8
6
C( , )
8
4
A、B两点在同一列,数对的第一个数相同。
B、C两点在同一行,数对的第二个数相同。
D、C两点在同一列,数对的第一个数相同。
A、D两点在同一行,数对的第二个数相同。
8
6
拓展提升
55°
2.学校在书店东偏南35°方向600米处,书店在学校( )偏( )( )°的方向( )米处。
观测点和被观测点互换,方向相反,角度和距离不变。
学校
书店
学校在书店南偏东55°方向600米处,观测点是书店。
55°
书店在学校的哪个方向,观测点是学校。
北 西 55 600
123456
7
6
5
4
3
2
1
0
3.根据要求在下图中操作,并回答问题。
(1,4)
B
A
C
(1)用数对表示图中点A、B、C的位置。
(3,4)
(1,6)
(2)把三角形ABC绕点B逆时针旋转90°,用数对表示点A、B、C旋转后的位置。
(3,2)
(1,2)
123456
7
6
5
4
3
2
1
0
3.根据要求在下图中操作,并回答问题。
B
A
C
(3)以虚线为对称轴画出三角形ABC的对称图形A1B1C1,并用数对表示点A1、B1、C1的位置。
(3,4)
(4)把三角形A1B1C1向下平移4格,画出平移后的图形。
C1
(5,6)
(5,4)
A1
B1
123456
7
6
5
4
3
2
1
0
3.根据要求在下图中操作,并回答问题。
B
A
C
(5)用数对表示点A1、B1、C1平移后的位置。
(3,4)
说一说你发现了什么。
C1
(5,6)
(5,4)
A1
B1
(5,2)
(3,0)
(5,0)
向下平移后数对中第一个数(列数)不变,第二个数(行数)都减少了4。
4.同学们排成方队做操,从前面看小明的位置在(6,4),向后转之后,小明的位置在(3,5),请你算一算这个方队一共有多少人。
1
2
3
4
5
6
2
1
3
1
4
3
2
4
1
2
3
5
★
从前面看,小明在第6列第4行。
向后转之后,小明在第3列第5行。
由图可知,这个方队一共有8列、8行。
可以画图帮助理解题意。
(6+3-1)×(4+5-1)
=8×8
=64(人)
答:这个方队一共有64人。
4.同学们排成方队做操,从前面看小明的位置在(6,4),向后转之后,小明的位置在(3,5),请你算一算这个方队一共有多少人。
1
2
3
4
5
6
2
1
3
1
4
3
2
4
1
2
3
5
★
5.在夏令营活动中,小虎研究“藏宝图”,得到以下重要信息。
(1)找到宝塔北偏东50°方向300米处的点A。
300÷200=1.5(cm)
·
宝塔
北
A
60°
0 200米
50°
B
(2)找到宝塔南偏东60°方向400米处的点B。
400÷200=2(cm)
·
宝塔
北
A
30°
0 200米
40°
B
(3)把A、B两点连起来后,与正东方向相交的位置就是宝藏所在地,请用“ ”标出宝藏的地点。
5.在夏令营活动中,小虎研究“藏宝图”,得到以下重要信息。
总复习
图形与位置
七
2.图形与几何
(教材第99页)
我们学过哪些确定位置的方法?
在确定位置时,还应用过哪些知识?
还可以用数对
来表示位置。
用东、南、西、北 表示物体之间的位 置关系。
用上、下、前、后、左、右确定位置。
可以用方向和距离 确定位置。
图形与位置
用数对表示具体情境中物体位置
在方格纸上用数对确定物体位置
根据方向和距离确定物体的相对位置
描述并绘制路线图
在平面图上确定物体的位置
用数对表示物体的位置
先列(竖排)后行(横排),用小括号把列数和行数相对应的数字括起来,并用逗号隔开,即(列数,行数)。
竖排叫作列,横排叫作行。确定第几列一般
从左往右数,确定第几行一般从前往后数。
用数对确定物体的位置。
如果第一个数字相同,则表示在同一列;
如果第二个数字相同,则表示在同一行。
(a ,b)
列数
行数
用方向和距离确定物体的位置
确定观测点,画出方向标。
把观测点和观察目标连起来,与南北方向形成一个角,测量出该角的度数。
用方向和距离确定物体的位置
测量出观测点和观测目标的图上距离,根据比例尺与图上距离计算出实际距离。
根据方向和距离两个条件就能精确地确定平面内物体的位置。
两种确定位置的方法有怎样的联系和区别
用数对确定位置,一定要先说列,再说行。
用方向和距离确定位置时,一定要先找准物体或地点所在的方向区域,一般先说夹角的方向。
两种确定位置的方式都要先确定标准,位置具有相对性。
描述行走路线
描述行走路线时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所行走的方向和距离,即每一步都要说清起点在哪,沿着什么方向走了多远的路程,终点在哪。
(1)孔雀园在大门的哪一面?
1.下面是青山动物园平面图的一部分。
孔雀园在大门的北面。
(教材第99页)
1.下面是青山动物园平面图的一部分。
(2)猴山在孔雀园的哪一面?狮虎山、鹿岛和熊猫馆呢?
猴山在孔雀园的东南面,狮虎山在孔雀园的东北面,鹿岛在孔雀园的西北面,熊猫馆在孔雀园的西南面。
(3)小华设计了一条游览路线,并用如下方法表示:
(6,1)→(9,3)→(10,6)→(6,4)→(2,5)→(3,2)→(6,1)
先按顺序说说小华游览的景点,再设计一条不同的游览路线,与同学交流。
小华从大门(6,1)→ 猴山(9,3)→ 狮虎山(10,6)→孔雀园(6,4)→ 鹿岛(2,5)→ 熊猫馆(3,2)→ 大门(6,1)
(路线不唯一)
2.以电视塔为观测点、填一填,画一画。
(1)市民广场在电视塔( )方向( )米处,电信大楼在电视塔( )方向( )米处。
正东
160
240
正北
2.以电视塔为观测点、填一填,画一画。
(2)市政府在电视塔( )偏( )( )°方向( )米处,少年宫在电视塔( )偏( )( )°方向( )米处。
北
50
东
320
南
35
西
240
2.以电视塔为观测点、填一填,画一画。
(3)百货大楼在电视塔南偏东30°方向240米处,图书馆在电视塔北偏西45°方向320米处。在图中表示出百货大楼和图书馆的位置。
3.下面是2路公共汽车行驶的路线图。说一说从红梅新村到淮定桥的行驶方向和经过的站点。
2路公共汽车从红梅新村出发,先向北行驶到东园,再向北偏西方向行驶到兴民巷,再向西行驶到青年路,再向南偏西方向行驶到时代广场,再向西先后行驶到电子城和科技大厦,再向南行驶到城中公园,再向北偏西方向行驶到钟楼,再向西行驶到西门,最后向北行驶到淮定桥。
4.你的家乡在哪里?有哪些旅游景点?小组合作,一部分同学扮演外地客人,其他同学试着介绍家乡的位置、旅游景点,以及游览路线。
1.(1)在下面的方格图中画出一个三角形,三个顶点分别为A(1,6)、B(1,3)、C(3,3),这个三角形是( )三角形。
123456789
10 11 12 13 14 15
76543210
直角
·A
·B
·
C
巩固练习
(2)画出这个三角形先向下平移2格,再向右平移6格后的图形,并用数对标出三个顶点的位置。
123456789
10 11 12 13 14 15
76543210
·A
·B
·
C
(7,4)
(7,1)
(9,1)
位置发生变化,表示的数对也发生变化。
76543210
(3)每个小方格的边长表示1 cm,以AB所在的直线为轴将三角形ABC旋转一周,将得到一个( ),它的体积是( )cm3。
123456789
10 11 12 13 14 15
·A
·B
·
C
(7,4)
(7,1)
(9,1)
圆锥
圆锥的底面半径是2 cm,高是3 cm。
3.14×22×3÷3=12.56(cm3)
12.56
2.如下图,以电视塔为观测点,填一填。
(1)市民广场在电视塔的( )方向( )米处。
正东
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
(2)电信大楼在电视塔的( )偏( )( )°方向( )米处。
160
(3)少年宫在电视塔的( )偏( )( )°方向( )米处。
北
40
东
240
南
30
西
240
电信业务,她首先要从市民广场往( )方向步行( )米到达电视塔,再往( )偏( )( )°方向行( )米即可到达。
正西
(2)王阿姨的家住在市民广场附近,一天早晨,她打算从市民广场出发,步行经过电视塔去电信大楼办理
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
160
北
40
东
240
·
从“市民广场”出发时观测点是“市民广场”。
从“电视塔”出发时观测点是“电视塔”。
0
9
3.如下图,平行四边形ABCD的三个顶点A、B、C的位置用数对表示分别是(4,6)、(1,3)、(5,3),那么顶点D的位置用数对表示为( )。
8,6
4
6
1
3
5
2
3
8
6
7
4格
1
2
4
5
7
D
C
B
A
4格
根据已知的三个顶点的数对画出带刻度的方格纸,就可以用数对表示出D点的位置。
4.下面是某地12路公交车的行驶路线图。
(1)12路公交车从游乐园出发,向( )方向行1.5 km到达邮局,再向( )偏( )( )°方向行( )km到达医院。
正东
北
游乐园
邮局
医院
1km
超市
电影院
书店
1.8km
2.5km
40°
60°
70°
北
东
40
2
2km
1.5km
4.下面是某地12路公交车的行驶路线图。
(2)从超市向( )偏( )( )°方向行( )km到达电影院,再向( )偏( )( )°方向行( )km到达书店。
北
游乐园
1.5km
邮局
2km
医院
超市
电影院
书店
1.8km
2.5km
40°
60°
70°
南
东
60
1.8
北
东
70
2.5
1km
1.在方格纸上画一个长方形,其中三个顶点的位置分别是(3,4),(8,4),(3,6),那么第四个顶点的位置是( , )。
A( , )
3
6
B( , )
3
4
D( , )
8
6
C( , )
8
4
A、B两点在同一列,数对的第一个数相同。
B、C两点在同一行,数对的第二个数相同。
D、C两点在同一列,数对的第一个数相同。
A、D两点在同一行,数对的第二个数相同。
8
6
拓展提升
55°
2.学校在书店东偏南35°方向600米处,书店在学校( )偏( )( )°的方向( )米处。
观测点和被观测点互换,方向相反,角度和距离不变。
学校
书店
学校在书店南偏东55°方向600米处,观测点是书店。
55°
书店在学校的哪个方向,观测点是学校。
北 西 55 600
123456
7
6
5
4
3
2
1
0
3.根据要求在下图中操作,并回答问题。
(1,4)
B
A
C
(1)用数对表示图中点A、B、C的位置。
(3,4)
(1,6)
(2)把三角形ABC绕点B逆时针旋转90°,用数对表示点A、B、C旋转后的位置。
(3,2)
(1,2)
123456
7
6
5
4
3
2
1
0
3.根据要求在下图中操作,并回答问题。
B
A
C
(3)以虚线为对称轴画出三角形ABC的对称图形A1B1C1,并用数对表示点A1、B1、C1的位置。
(3,4)
(4)把三角形A1B1C1向下平移4格,画出平移后的图形。
C1
(5,6)
(5,4)
A1
B1
123456
7
6
5
4
3
2
1
0
3.根据要求在下图中操作,并回答问题。
B
A
C
(5)用数对表示点A1、B1、C1平移后的位置。
(3,4)
说一说你发现了什么。
C1
(5,6)
(5,4)
A1
B1
(5,2)
(3,0)
(5,0)
向下平移后数对中第一个数(列数)不变,第二个数(行数)都减少了4。
4.同学们排成方队做操,从前面看小明的位置在(6,4),向后转之后,小明的位置在(3,5),请你算一算这个方队一共有多少人。
1
2
3
4
5
6
2
1
3
1
4
3
2
4
1
2
3
5
★
从前面看,小明在第6列第4行。
向后转之后,小明在第3列第5行。
由图可知,这个方队一共有8列、8行。
可以画图帮助理解题意。
(6+3-1)×(4+5-1)
=8×8
=64(人)
答:这个方队一共有64人。
4.同学们排成方队做操,从前面看小明的位置在(6,4),向后转之后,小明的位置在(3,5),请你算一算这个方队一共有多少人。
1
2
3
4
5
6
2
1
3
1
4
3
2
4
1
2
3
5
★
5.在夏令营活动中,小虎研究“藏宝图”,得到以下重要信息。
(1)找到宝塔北偏东50°方向300米处的点A。
300÷200=1.5(cm)
·
宝塔
北
A
60°
0 200米
50°
B
(2)找到宝塔南偏东60°方向400米处的点B。
400÷200=2(cm)
·
宝塔
北
A
30°
0 200米
40°
B
(3)把A、B两点连起来后,与正东方向相交的位置就是宝藏所在地,请用“ ”标出宝藏的地点。
5.在夏令营活动中,小虎研究“藏宝图”,得到以下重要信息。
