第4章 几何图形初步 章末综合训练 人教版七年级数学 上册(无答案)
文档属性
| 名称 | 第4章 几何图形初步 章末综合训练 人教版七年级数学 上册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 454.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 10:25:34 | ||
图片预览



文档简介
第4章 几何图形初步 章末综合训练
一、单选题
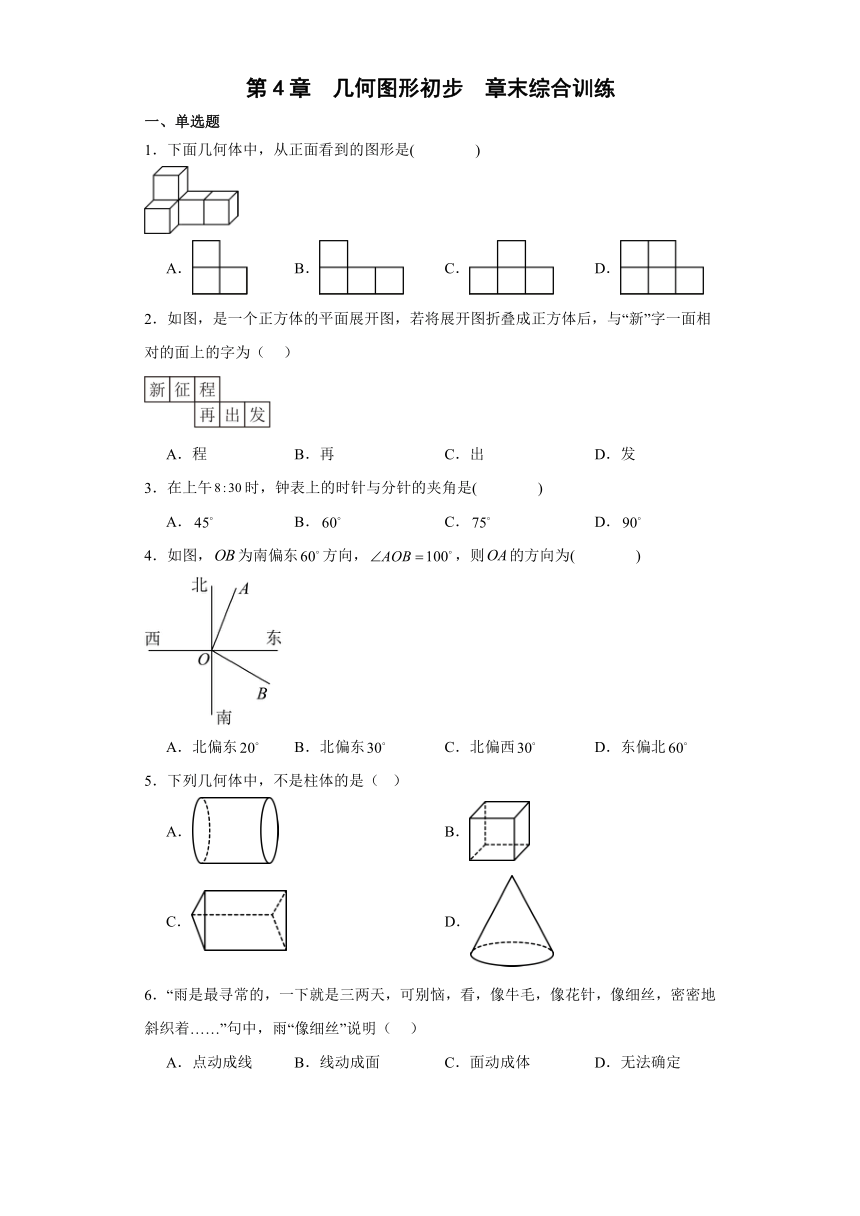
1.下面几何体中,从正面看到的图形是( )
A. B. C. D.
2.如图,是一个正方体的平面展开图,若将展开图折叠成正方体后,与“新”字一面相对的面上的字为( )
A.程 B.再 C.出 D.发
3.在上午时,钟表上的时针与分针的夹角是( )
A. B. C. D.
4.如图,为南偏东方向,,则的方向为( )
A.北偏东 B.北偏东 C.北偏西 D.东偏北
5.下列几何体中,不是柱体的是( )
A. B.
C. D.
6.“雨是最寻常的,一下就是三两天,可别恼,看,像牛毛,像花针,像细丝,密密地斜织着……”句中,雨“像细丝”说明( )
A.点动成线 B.线动成面 C.面动成体 D.无法确定
7.如图,A、两个村庄在一条河(不计河的宽度)的两侧,现要建一座码头,使它到A、两个村庄的距离之和最小,连接交于点,则点即为所求的码头的位置,这样做的理由是( )
A.两点之间,线段最短 B.射线只有一个端点
C.两点之间,直线最短 D.两点确定一条直线
8.如图所示,B,C是线段上任意两点,M是的中点,N是的中点,若,,则的长度是( )
A. B. C. D.以上都不对
9.如图,已知平分,且,则的度数为( )
A.100° B.120° C.135° D.150°
10.如图,点M在线段AN的延长线上,且线段,第一次操作:分别取线段和的中点、;第二次操作:分别取线段和的中点,;第三次操作:分别取线段和的中点,;…连续这样操作2023次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
二、填空题
11. .
12.一个角的余角比这个角的补角的一半还小25°,则这个角是 度.
13.已知,.若平分,平分,则的度数为 度.
14.如图,点C、D在线段上,点为中点,若,,则的长度是 .
15.已知点,,三点在同一条直线上,若,则以,,三点组成的这三条线段中,当其中一点是另两点组成的线段的中点时,线段的长为 .
16.如图1,一款暗插销由外壳,开关,锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到,锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知,,则 mm.
三、解答题
17.如图,已知不在同一直线上的A、B、C三点.
(1)画直线;
(2)画射线;
(3)画线段,并延长到D,使.
18.如图,C、D是线段上的两点,且D是线段的中点,,,求线段的长度.
19.如图已知点C为线段上一点,,D为的中点,E为上的点,且,若,求线段的长.
20.如图,O是直线上一点,是的平分线.
(1)若,求的度数;
(2)若,求的度数.
21.如图,线段,C是线段上一点,,D、E分别是、的中点.
(1)求线段的长;
(2)求线段的长.
22.已知,保持不动,的边与边重合,然后将绕点O按顺时针方向任意转动一个角度,(本题中研究的其它角的度数均小于)
(1)[特例分析]如图1,若,则_______°,_______°
(2)[一般化研究]如图2,若,随着的变化,探索与的数量关系,并说明理由.
(3)[继续一般化]随着的变化,直接写出与的数量关系、(结果用含的代数式表示).
23.点O为直线上一点,在直线AB同侧任作射线OC,OD,使得.
(1)如图1,过点O作射线,当恰好为的角平分线时,另作射线,使得平分,则的度数是___________°;
(2)如图2,过点O作射线,当恰好为的角平分线时,求出与的数量关系;
(3)过点O作射线,当恰好为的角平分线时,另作射线,使得平分,若,求出的度数.
24.已知点在数轴上,点为线段的中点.
(1)如图,点在线段上,点之间的距离为.
若点是数轴的原点,点表示的数为3,当时,求点表示的数;
若,且,求的值;
(2)若点表示的数分别为,其中,且两点关于原点对称,判断点为哪条线段的中点,并说明理由.
一、单选题
1.下面几何体中,从正面看到的图形是( )
A. B. C. D.
2.如图,是一个正方体的平面展开图,若将展开图折叠成正方体后,与“新”字一面相对的面上的字为( )
A.程 B.再 C.出 D.发
3.在上午时,钟表上的时针与分针的夹角是( )
A. B. C. D.
4.如图,为南偏东方向,,则的方向为( )
A.北偏东 B.北偏东 C.北偏西 D.东偏北
5.下列几何体中,不是柱体的是( )
A. B.
C. D.
6.“雨是最寻常的,一下就是三两天,可别恼,看,像牛毛,像花针,像细丝,密密地斜织着……”句中,雨“像细丝”说明( )
A.点动成线 B.线动成面 C.面动成体 D.无法确定
7.如图,A、两个村庄在一条河(不计河的宽度)的两侧,现要建一座码头,使它到A、两个村庄的距离之和最小,连接交于点,则点即为所求的码头的位置,这样做的理由是( )
A.两点之间,线段最短 B.射线只有一个端点
C.两点之间,直线最短 D.两点确定一条直线
8.如图所示,B,C是线段上任意两点,M是的中点,N是的中点,若,,则的长度是( )
A. B. C. D.以上都不对
9.如图,已知平分,且,则的度数为( )
A.100° B.120° C.135° D.150°
10.如图,点M在线段AN的延长线上,且线段,第一次操作:分别取线段和的中点、;第二次操作:分别取线段和的中点,;第三次操作:分别取线段和的中点,;…连续这样操作2023次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
二、填空题
11. .
12.一个角的余角比这个角的补角的一半还小25°,则这个角是 度.
13.已知,.若平分,平分,则的度数为 度.
14.如图,点C、D在线段上,点为中点,若,,则的长度是 .
15.已知点,,三点在同一条直线上,若,则以,,三点组成的这三条线段中,当其中一点是另两点组成的线段的中点时,线段的长为 .
16.如图1,一款暗插销由外壳,开关,锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到,锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知,,则 mm.
三、解答题
17.如图,已知不在同一直线上的A、B、C三点.
(1)画直线;
(2)画射线;
(3)画线段,并延长到D,使.
18.如图,C、D是线段上的两点,且D是线段的中点,,,求线段的长度.
19.如图已知点C为线段上一点,,D为的中点,E为上的点,且,若,求线段的长.
20.如图,O是直线上一点,是的平分线.
(1)若,求的度数;
(2)若,求的度数.
21.如图,线段,C是线段上一点,,D、E分别是、的中点.
(1)求线段的长;
(2)求线段的长.
22.已知,保持不动,的边与边重合,然后将绕点O按顺时针方向任意转动一个角度,(本题中研究的其它角的度数均小于)
(1)[特例分析]如图1,若,则_______°,_______°
(2)[一般化研究]如图2,若,随着的变化,探索与的数量关系,并说明理由.
(3)[继续一般化]随着的变化,直接写出与的数量关系、(结果用含的代数式表示).
23.点O为直线上一点,在直线AB同侧任作射线OC,OD,使得.
(1)如图1,过点O作射线,当恰好为的角平分线时,另作射线,使得平分,则的度数是___________°;
(2)如图2,过点O作射线,当恰好为的角平分线时,求出与的数量关系;
(3)过点O作射线,当恰好为的角平分线时,另作射线,使得平分,若,求出的度数.
24.已知点在数轴上,点为线段的中点.
(1)如图,点在线段上,点之间的距离为.
若点是数轴的原点,点表示的数为3,当时,求点表示的数;
若,且,求的值;
(2)若点表示的数分别为,其中,且两点关于原点对称,判断点为哪条线段的中点,并说明理由.
