10.6 一次函数的应用课件(共15张PPT)2023-2024学年青岛版八年级下册数学
文档属性
| 名称 | 10.6 一次函数的应用课件(共15张PPT)2023-2024学年青岛版八年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 10:37:43 | ||
图片预览





文档简介
(共15张PPT)
第十章 一次函数
10.6 一次函数的应用
1.能用一次函数解决简单的实际问题.
任务一:用一次函数解决简单的实际问题.
活动1:和同伴一起交流,回答下列问题.
x(厘米) … 22 23 24 25 26 …
y(码) … 34 36 38 40 42 …
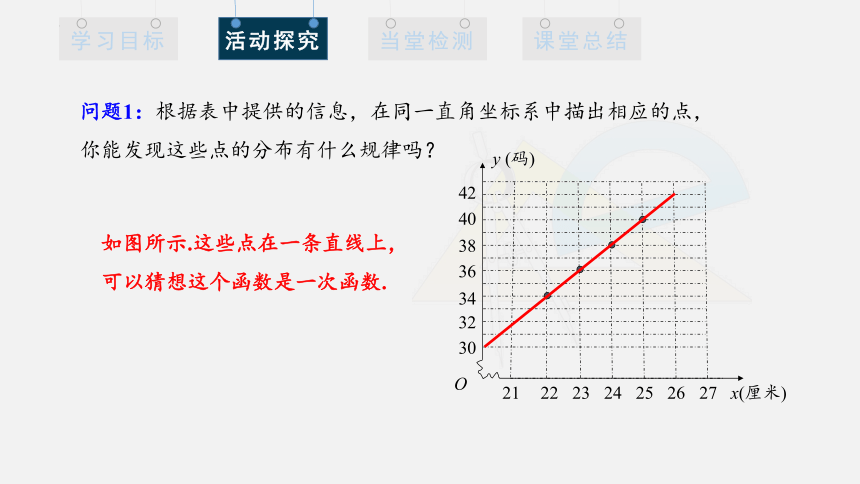
问题1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
问题1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
如图所示.这些点在一条直线上,可以猜想这个函数是一次函数.
O
选取点(22,34)及点(25,40)的坐标代入y=kx+b中,得
22k+b=34,
25k+b=40.
解得k=2, b=-10.
所以,一次函数的表达式为y=2x-10.
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
O
问题2:你能利用问题1中的图象,写出y与x的函数表达式吗?
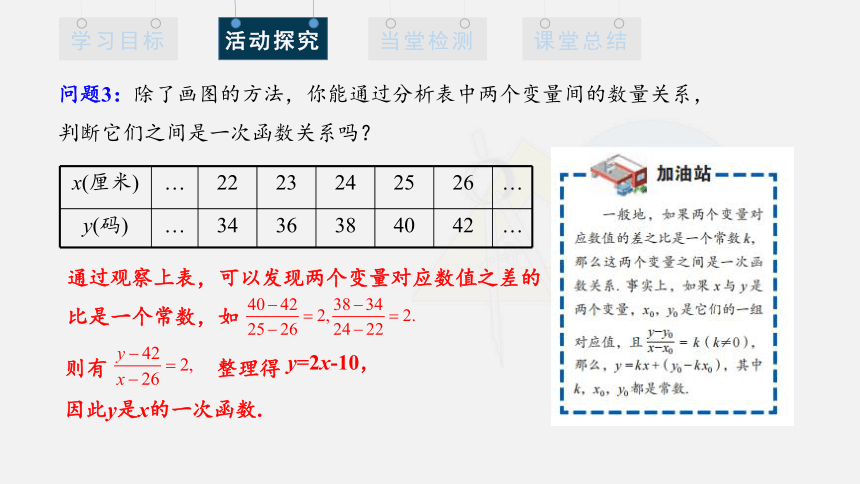
问题3:除了画图的方法,你能通过分析表中两个变量间的数量关系,
判断它们之间是一次函数关系吗?
x(厘米) … 22 23 24 25 26 …
y(码) … 34 36 38 40 42 …
通过观察上表,可以发现两个变量对应数值之差的比是一个常数,如
y=2x-10,
则有 整理得
因此y是x的一次函数.
活动小结
①对于这类题,我们可以对照表格在坐标系内大致描出各点,观察他们是否在一条直线附近波动,猜想它们近似地满足一次函数关系,再从上述各组数据中任选两组数据,利用待定系数法,可求出它的函数表达式.
②将剩余的一些对应数值代入所求出的函数表达式中进行检验,检验所建立的函数模型是否正确.
情境:山青林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.根据相关资料,甲、乙两种树苗的成活率分别是85%,90%.
活动2:和同伴一起交流,完成下列问题.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
解:设购买甲种树苗x株,乙种树苗y株,根据题意,得
解得
经检验,方程组的解符合题意.∴购买甲种树苗500株,乙种树苗300株.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少株?
解:设购买甲种树苗m株,乙种树苗(800-m)株,由题意得
0.85m+0.9×(800-m)≥0.88×800,
解得 m≤320.
所以甲种树苗至多购买320株.
情境:山青林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.根据相关资料,甲、乙两种树苗的成活率分别是85%,90%.
解:设购买甲种树苗t株,购买树苗的费用为w元,由题意得
w=24t+30×(800-t)=-6t+24000,
∴w是t的一次函数,且由于k=-6<0,因此w随t增大而减小.
由(2)知t≤320,因此,当t最大即t=320时,w最小.
这时800-320=480,w=-6×320+24000=22080.
∴购买甲种树苗320株、乙种树苗480株,费用最低,最低费用为22080元.
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
1.某工厂加工一批机器,机器数y(个)和所用的时间t(小时)在坐标系中对应的一些点的位置如图所示,由此可求出y关于x的近似函数表达式为( )
B
A.y=2x+1 B.y=x+1 C.y= x+1 D.y=x+2
注意:根据两点确定一条直线,在确定直线的方程时,至少要验证两个点.
2.王老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,如图,那么到达乙地时油箱剩余油量是( )
A. 10升 B. 20升
C. 30升 D. 40升
B
3.声音的传播速度跟温度和传播的介质有关,经实验检测,不同气温下声音传播的速度如下表所示:
气温x(℃) 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
(1)能否用一次函数刻画这两个变量x和y的关系?如果能,写出y关于x的函数表达式.
解:由表中的数据可判定y与x成一次函数关系,所以设y=kx+b,把x=0,y=331与x=5,y=334分别代入解得:k=0.6,b=331,
所以y=0.6x+331.
(2)当气温x=22℃时,小明看到烟花燃放5秒后才听到声响,你能确定小明与燃放烟花所在地相距有多远吗
解:由(1)得y=0.6x+331,当x=22℃时,y=0.6×22+331=344.2(米/秒),故相距的距离=344.2×5=1721(米).
气温x(℃) 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
针对本课关键词“一次函数的应用”,说说你学到了什么?
在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数关系.当确定是一次函数关系时,可求出函数表达式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
第十章 一次函数
10.6 一次函数的应用
1.能用一次函数解决简单的实际问题.
任务一:用一次函数解决简单的实际问题.
活动1:和同伴一起交流,回答下列问题.
x(厘米) … 22 23 24 25 26 …
y(码) … 34 36 38 40 42 …
问题1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
问题1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
如图所示.这些点在一条直线上,可以猜想这个函数是一次函数.
O
选取点(22,34)及点(25,40)的坐标代入y=kx+b中,得
22k+b=34,
25k+b=40.
解得k=2, b=-10.
所以,一次函数的表达式为y=2x-10.
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
O
问题2:你能利用问题1中的图象,写出y与x的函数表达式吗?
问题3:除了画图的方法,你能通过分析表中两个变量间的数量关系,
判断它们之间是一次函数关系吗?
x(厘米) … 22 23 24 25 26 …
y(码) … 34 36 38 40 42 …
通过观察上表,可以发现两个变量对应数值之差的比是一个常数,如
y=2x-10,
则有 整理得
因此y是x的一次函数.
活动小结
①对于这类题,我们可以对照表格在坐标系内大致描出各点,观察他们是否在一条直线附近波动,猜想它们近似地满足一次函数关系,再从上述各组数据中任选两组数据,利用待定系数法,可求出它的函数表达式.
②将剩余的一些对应数值代入所求出的函数表达式中进行检验,检验所建立的函数模型是否正确.
情境:山青林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.根据相关资料,甲、乙两种树苗的成活率分别是85%,90%.
活动2:和同伴一起交流,完成下列问题.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
解:设购买甲种树苗x株,乙种树苗y株,根据题意,得
解得
经检验,方程组的解符合题意.∴购买甲种树苗500株,乙种树苗300株.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少株?
解:设购买甲种树苗m株,乙种树苗(800-m)株,由题意得
0.85m+0.9×(800-m)≥0.88×800,
解得 m≤320.
所以甲种树苗至多购买320株.
情境:山青林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.根据相关资料,甲、乙两种树苗的成活率分别是85%,90%.
解:设购买甲种树苗t株,购买树苗的费用为w元,由题意得
w=24t+30×(800-t)=-6t+24000,
∴w是t的一次函数,且由于k=-6<0,因此w随t增大而减小.
由(2)知t≤320,因此,当t最大即t=320时,w最小.
这时800-320=480,w=-6×320+24000=22080.
∴购买甲种树苗320株、乙种树苗480株,费用最低,最低费用为22080元.
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
1.某工厂加工一批机器,机器数y(个)和所用的时间t(小时)在坐标系中对应的一些点的位置如图所示,由此可求出y关于x的近似函数表达式为( )
B
A.y=2x+1 B.y=x+1 C.y= x+1 D.y=x+2
注意:根据两点确定一条直线,在确定直线的方程时,至少要验证两个点.
2.王老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,如图,那么到达乙地时油箱剩余油量是( )
A. 10升 B. 20升
C. 30升 D. 40升
B
3.声音的传播速度跟温度和传播的介质有关,经实验检测,不同气温下声音传播的速度如下表所示:
气温x(℃) 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
(1)能否用一次函数刻画这两个变量x和y的关系?如果能,写出y关于x的函数表达式.
解:由表中的数据可判定y与x成一次函数关系,所以设y=kx+b,把x=0,y=331与x=5,y=334分别代入解得:k=0.6,b=331,
所以y=0.6x+331.
(2)当气温x=22℃时,小明看到烟花燃放5秒后才听到声响,你能确定小明与燃放烟花所在地相距有多远吗
解:由(1)得y=0.6x+331,当x=22℃时,y=0.6×22+331=344.2(米/秒),故相距的距离=344.2×5=1721(米).
气温x(℃) 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
针对本课关键词“一次函数的应用”,说说你学到了什么?
在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数关系.当确定是一次函数关系时,可求出函数表达式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
