黑龙江省哈尔滨市通河县2022-2023学年八年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市通河县2022-2023学年八年级(下)期末数学试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 620.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 09:56:01 | ||
图片预览



文档简介
2022-2023学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷
一、选择题(每小题3分,共30分)
1.(3分)的值是( )
A.±4 B.﹣4
C.4 D.以上答案都不对
2.(3分)下列各线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.3,4,5 D.4,5,6
3.(3分)下列计算中,结果错误的是( )
A. B. C. D.
4.(3分)在下列函数中是正比例函数的是( )
A.y=3x﹣4 B.y=﹣2x+1 C.y=3x D.y=4
5.(3分)直线y=﹣5x向上平移2个单位长度,得到的直线的解析式为( )
A.y=5x+2 B.y=﹣5x+2 C.y=5x﹣2 D.y=﹣5x﹣2
6.(3分)直线y=2x+1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(3分)在下面的一组数据:2,3,2,2,2,5,4中众数是( )
A.5 B.4 C.3 D.2
8.(3分)下列性质中,矩形具有而一般的平行四边形不具有的是( )
A.对边相等 B.对角相等
C.对角线相等 D.对边平行
9.(3分)下列各点中在函数y=4x的图象上的点是( )
A.(1,2) B.(1,3) C.(1,4) D.(1,5)
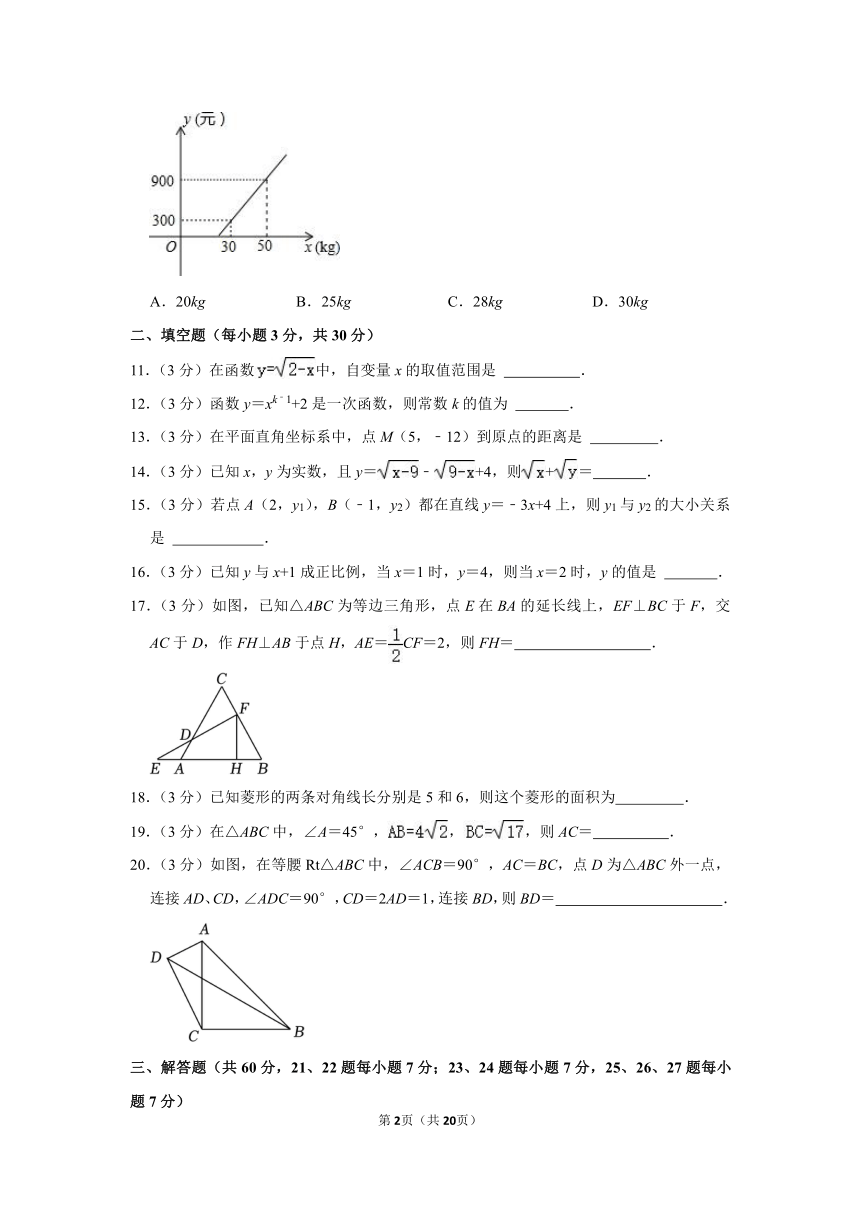
10.(3分)某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20kg B.25kg C.28kg D.30kg
二、填空题(每小题3分,共30分)
11.(3分)在函数中,自变量x的取值范围是 .
12.(3分)函数y=xk﹣1+2是一次函数,则常数k的值为 .
13.(3分)在平面直角坐标系中,点M(5,﹣12)到原点的距离是 .
14.(3分)已知x,y为实数,且y=﹣+4,则+= .
15.(3分)若点A(2,y1),B(﹣1,y2)都在直线y=﹣3x+4上,则y1与y2的大小关系是 .
16.(3分)已知y与x+1成正比例,当x=1时,y=4,则当x=2时,y的值是 .
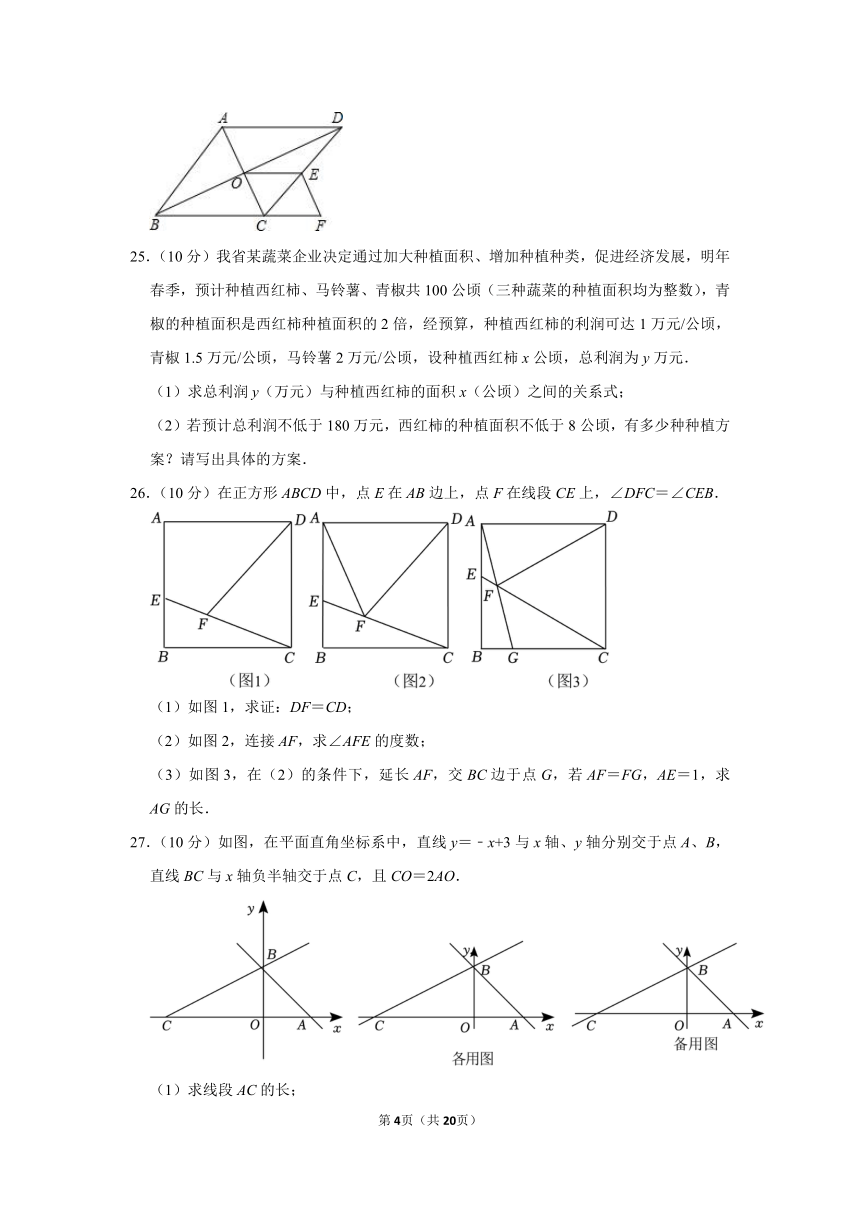
17.(3分)如图,已知△ABC为等边三角形,点E在BA的延长线上,EF⊥BC于F,交AC于D,作FH⊥AB于点H,AE=CF=2,则FH= .
18.(3分)已知菱形的两条对角线长分别是5和6,则这个菱形的面积为 .
19.(3分)在△ABC中,∠A=45°,,,则AC= .
20.(3分)如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC外一点,连接AD、CD,∠ADC=90°,CD=2AD=1,连接BD,则BD= .
三、解答题(共60分,21、22题每小题7分;23、24题每小题7分,25、26、27题每小题7分)
21.(7分)先化简,再求值:,其中x=+1.
22.(7分)如图,图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
(1)如图1,当点E为AB的中点时,请在AD上找到一点P(点P在小正方形的顶点上且不同于点F),连接EP,CP,使得△EPC为Rt△,且∠EPC=90°;
(2)请在图2中以EG为一边画矩形EGMQ(非正方形),使点M、Q均在小正方形的顶点上并直接写出矩形EGMQ的面积.
23.(8分)如图,一艘轮船以每小时35海里的速度向东航行,在A处观测到在它的东北方向(北偏东45°)点C处有一艘捕渔船,2小时后轮船到达点B处,突然收到渔船的求救信号,此时观测到渔船C位于点B的北偏东15°方向上.
(1)求∠ACB的度数;
(2)轮船收到求救信号后,立即沿BC以每小时海里的速度赶往C处救援,那么轮船需多少小时赶到C处?
24.(8分)在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=BC.
(1)求证:四边形OCEF是平行四边形;
(2)连接DF,如果DF⊥CF,请你写出图中所有的等边三角形.
25.(10分)我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,明年春季,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式;
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?请写出具体的方案.
26.(10分)在正方形ABCD中,点E在AB边上,点F在线段CE上,∠DFC=∠CEB.
(1)如图1,求证:DF=CD;
(2)如图2,连接AF,求∠AFE的度数;
(3)如图3,在(2)的条件下,延长AF,交BC边于点G,若AF=FG,AE=1,求AG的长.
27.(10分)如图,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于点A、B,直线BC与x轴负半轴交于点C,且CO=2AO.
(1)求线段AC的长;
(2)动点P从点C出发沿射线CA以每秒1个单位的速度运动,连接BP,设点P的运动时间为t(秒),△BPO的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,在线段BC上是否存在点D,连接DP,使得△BDP是以BP为直角边的等腰直角三角形,若存在,请求出t的值,若不存在,请说明理由.
2022-2023学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)的值是( )
A.±4 B.﹣4
C.4 D.以上答案都不对
【解答】解:=4.
故选:C.
2.(3分)下列各线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.3,4,5 D.4,5,6
【解答】解:∵22+32≠42,
∴A不能构成直角三角形,
∵32+42≠62,
∴B不能构成直角三角形,
∵32+42=52,
∴C能构成直角三角形,
∵42+52≠62,
∴D不能构成直角三角形,
故选:C.
3.(3分)下列计算中,结果错误的是( )
A. B. C. D.
【解答】解:A、与不属于同类二次根式,不能运算,故A符合题意;
B、5﹣2=3,故B不符合题意;
C、÷=,故C不符合题意;
D、(﹣)2=2,故D不符合题意;
故选:A.
4.(3分)在下列函数中是正比例函数的是( )
A.y=3x﹣4 B.y=﹣2x+1 C.y=3x D.y=4
【解答】解:A.y=3x﹣4为一次函数,但不是正比例函数,所以A选项不符合题意;
B.y=﹣2x+1为一次函数,但不是正比例函数,所以B选项不符合题意;
C.y=3x是正比例函数,所以C选项符合题意;
D.y=4为常函数,所以D选项不符合题意;
故选:C.
5.(3分)直线y=﹣5x向上平移2个单位长度,得到的直线的解析式为( )
A.y=5x+2 B.y=﹣5x+2 C.y=5x﹣2 D.y=﹣5x﹣2
【解答】解:将直线y=﹣5x向上平移2个单位长度,得到的直线的解析式为:y=﹣5x+2.
故选:B.
6.(3分)直线y=2x+1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵y=2x﹣1,k=2>0,b=1,
∴该函数经过第一、三、二象限,不经过第四象限,
故选:D.
7.(3分)在下面的一组数据:2,3,2,2,2,5,4中众数是( )
A.5 B.4 C.3 D.2
【解答】解:这组数据的众数为2,
故选:D.
8.(3分)下列性质中,矩形具有而一般的平行四边形不具有的是( )
A.对边相等 B.对角相等
C.对角线相等 D.对边平行
【解答】解:矩形的特性是:四个角都是直角,对角线相等.
故选:C.
9.(3分)下列各点中在函数y=4x的图象上的点是( )
A.(1,2) B.(1,3) C.(1,4) D.(1,5)
【解答】解:当x=1时,y=4×1=4,4≠2,
∴点(1,4)在函数y=4x的图象上.
故选:C.
10.(3分)某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20kg B.25kg C.28kg D.30kg
【解答】解:设y与x的函数关系式为y=kx+b,
由题意可知,
解得,
所以函数关系式为y=30x﹣600,
当y=0时,即30x﹣600=0,所以x=20.
故选:A.
二、填空题(每小题3分,共30分)
11.(3分)在函数中,自变量x的取值范围是 x≤2 .
【解答】解:由题意,得
2﹣x≥0,解得x≤2,
故答案为:x≤2.
12.(3分)函数y=xk﹣1+2是一次函数,则常数k的值为 2 .
【解答】解:∵函数y=xk﹣1+2是一次函数,
∴k﹣1=1,
∴k=2,
故答案为:2.
13.(3分)在平面直角坐标系中,点M(5,﹣12)到原点的距离是 13 .
【解答】解:由勾股定理得,点M(5,﹣12)到原点的距离为,
故答案为:13.
14.(3分)已知x,y为实数,且y=﹣+4,则+= 5 .
【解答】解:依题意得:,
解得x=9,
所以y=4
故+=3+2=5.
故答案为:5.
15.(3分)若点A(2,y1),B(﹣1,y2)都在直线y=﹣3x+4上,则y1与y2的大小关系是 y1<y2 .
【解答】解:∵k=﹣3<0,
∴y随x的增大而减小,
又∵点A(2,y1),B(﹣1,y2)都在直线y=﹣3x+4上,且2>﹣1,
∴y1<y2.
故答案为:y1<y2.
16.(3分)已知y与x+1成正比例,当x=1时,y=4,则当x=2时,y的值是 6 .
【解答】解:设y=k(x+1)(k≠0),
把x=1,y=4代入,得k(1+1)=4.
解得k=2.
所以当x=2时,y=2(2+1)=6.
故答案为:6.
17.(3分)如图,已知△ABC为等边三角形,点E在BA的延长线上,EF⊥BC于F,交AC于D,作FH⊥AB于点H,AE=CF=2,则FH= 3 .
【解答】解:∵△ABC为等边三角形,
∴∠C=∠B=∠CAB=60°,
∵EF⊥BC,
∴∠DFC=90°,
∵CF=4,
∴CD=2CF=8,∠CDF=30°,
∴∠ADE=30°,
∴∠E=∠CAB﹣∠ADE=30°,
∴EA=AD=2,
∴AC=10,
∴BF=6,
∴BH=3,
∴FH==3,
故答案为:3.
18.(3分)已知菱形的两条对角线长分别是5和6,则这个菱形的面积为 15 .
【解答】解:∵菱形的两条对角线长分别是5和6,
∴这个菱形的面积为5×6÷2=15.
故答案为:15.
19.(3分)在△ABC中,∠A=45°,,,则AC= 5或3 .
【解答】解:过B作BH⊥AC于H,
①当H在边AC上时,如图:
∵∠A=45°,BH⊥AC,
∴△ABH是等腰直角三角形,
∴AH=BH==4,
在Rt△BHC中,
CH===1,
∴AC=AH+CH=4+1=5;
②当H在边AC延长线上时,如图:
同理可得AH=BH=4,CH=1,
∴AC=AH﹣CH=3;
综上所述,AC的长为5或3;
故答案为:5或3.
20.(3分)如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC外一点,连接AD、CD,∠ADC=90°,CD=2AD=1,连接BD,则BD= .
【解答】解:延长AD交BC的延长线于E,过点D作DF⊥CE于点F,
∵CD=2AD=1,∠ADC=90°,
∴AC==,
设DE=a,
∴,
解得a=2,
∴DE=2,
∴CE==,
∵DE,
∴,
∴CF==,
∵CB=AC=,
∴BF=BC+CF=,
∴BD==.
故答案为:.
三、解答题(共60分,21、22题每小题7分;23、24题每小题7分,25、26、27题每小题7分)
21.(7分)先化简,再求值:,其中x=+1.
【解答】解:原式=
=
=.
当x=+1时,原式=.
22.(7分)如图,图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
(1)如图1,当点E为AB的中点时,请在AD上找到一点P(点P在小正方形的顶点上且不同于点F),连接EP,CP,使得△EPC为Rt△,且∠EPC=90°;
(2)请在图2中以EG为一边画矩形EGMQ(非正方形),使点M、Q均在小正方形的顶点上并直接写出矩形EGMQ的面积.
【解答】解:(1)如图1,△EPC即为所求;
(2)如图2,矩形EGMQ即为所求;
矩形EGMQ面积=EG EQ=×=10.
23.(8分)如图,一艘轮船以每小时35海里的速度向东航行,在A处观测到在它的东北方向(北偏东45°)点C处有一艘捕渔船,2小时后轮船到达点B处,突然收到渔船的求救信号,此时观测到渔船C位于点B的北偏东15°方向上.
(1)求∠ACB的度数;
(2)轮船收到求救信号后,立即沿BC以每小时海里的速度赶往C处救援,那么轮船需多少小时赶到C处?
【解答】解:(1)∵∠DAC=45°,∠DAB=90°,
∴∠CAB=45°,
∵∠EBC=15°,∠ABE=90°,
∴∠ABC=105°,
∴∠ACB=180°﹣∠ABC﹣∠CAB=180°﹣105°﹣45°=30°;
(2)过B作BF⊥AC于F,
∴∠FAB=∠FBA=45°,
∴AF=BF,
∵AB=35×2=70(海里),AB2=AF2+BF2,
∴(海里),
∵∠ACB=30°,
∴(海里),
∵,
∴轮船需小时赶到C处.
24.(8分)在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=BC.
(1)求证:四边形OCEF是平行四边形;
(2)连接DF,如果DF⊥CF,请你写出图中所有的等边三角形.
【解答】(1)证明:∵四边形ABCD是菱形,
∴BO=DO,
∵E点是边CD的中点,
∴OE是△BDC的中位线,
∴OE∥BC且OE=BC,
∵CF=BC,
∴OE=CF,
∵OE∥CF,
∴四边形OCFE是平行四边形;
(2)解:∵DF⊥CF,E点是边CD的中点,
∴EF=,
∵CE=,
CF==CD,
∴△ECF为等边三角形;
∵四边形OCFE是平行四边形,
∴OC=EF=CE=CF=OE,
∴△OCE为等边三角形;
∵△ECF为等边三角形,
∴∠ECF=60°,
∴∠ABC=60°,
∵四边形ABCD是菱形,
∴△ABC为等边三角形;
同理得△ADC为等边三角形;
∴图中的等边三角形有:△OCE,△ECF,△ABC,△ADC
25.(10分)我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,明年春季,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式;
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?请写出具体的方案.
【解答】解:(1)由题意y=x+1.5×2x+2(100﹣3x)=﹣2x+200,
所以总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式为y=x+1.5×2x+2(100﹣3x)=﹣2x+200.
(2)由题意﹣2x+200≥180,
解得x≤10,
∵x≥8,
∴8≤x≤10.
∵x为整数,
∴x=8,9,10.
∴有3种种植方案,
方案一:种植西红柿8公顷、马铃薯76公顷、青椒16公顷.
方案二:种植西红柿9公顷、马铃薯73公顷、青椒18公顷.
方案三:种植西红柿10公顷、马铃薯70公顷、青椒20公顷.
26.(10分)在正方形ABCD中,点E在AB边上,点F在线段CE上,∠DFC=∠CEB.
(1)如图1,求证:DF=CD;
(2)如图2,连接AF,求∠AFE的度数;
(3)如图3,在(2)的条件下,延长AF,交BC边于点G,若AF=FG,AE=1,求AG的长.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,
∴∠CEB+∠BCE=90°,∠BCE+∠DCF=90°,
∴∠CEB=∠DCF,
∵∠DFC=∠CEB,
∴∠DFC=∠DCF,
∴DF=CD;
(2)解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
由(1)得DF=CD,
∴AD=DF=CD,
∴∠DAF=∠DFA,∠DFC=∠DCF,
在四边形ADCF中,∠DAF+∠AFC+∠DCF=360°﹣∠ADC=360°﹣90°=270°,
∴∠DAF+∠DFA+∠DFC+∠DCF=270°,
∴2∠DFA+2∠DFC=2∠AFC=270°,
∴∠AFC=135°,
∴∠AFE=180°﹣∠AFC=180°﹣135°=45°;
(3)解:如图3,延长CE交DA延长线于点H,过G作GK⊥CF于点K,
则∠CKG=∠FKG=90°,
∵四边形ABCD是正方形,
∴∠ADC=∠BAD=90°,AD∥BC,
∴∠H=∠FCG,∠HAF=∠CGF,
∵AF=FG,
∴△AFH≌△GFC(AAS),
∴AH=CG,FH=CF,
∵∠ADC=90°,
∴DF=CF,
由(1)得:DF=CD,
∴DF=CF=CD,
∴△DCF是等边三角形,
∴∠DCH=60°,
∴∠H=∠HCG=90°﹣60°=30°,
∠HAE=180°﹣90°=90°,
在Rt△AHE中,EH=2AE=2,
由勾股定理得:AH===,
∴CG=AH=,
在Rt△CGK中,KG=CG=×=,
在Rt△FKG中,∠KFG=∠AFE=45°,
∴△FKG是等腰直角三角形,
∴FK=KG=,
由勾股定理得:FG===,
∴AG=2FG=2×=.
27.(10分)如图,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于点A、B,直线BC与x轴负半轴交于点C,且CO=2AO.
(1)求线段AC的长;
(2)动点P从点C出发沿射线CA以每秒1个单位的速度运动,连接BP,设点P的运动时间为t(秒),△BPO的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,在线段BC上是否存在点D,连接DP,使得△BDP是以BP为直角边的等腰直角三角形,若存在,请求出t的值,若不存在,请说明理由.
【解答】解:(1)把x=0代入y=﹣x+3,y=3,
∴B(0,3),
把y=0代入y=﹣x+3,x=3,
∴A(3,0),
∴AO=3,
∵CO=2AO,
∴CO=6,
∴C(﹣6,0);
∴AC=6+3=9;
(2)∵C(﹣6,0),动点P从点C出发沿射线CA以每秒1个单位的速度运动,
∴CP=t,
∴P(﹣6+t,0),
∴OP=|6﹣t|,
∴S=×3×|6﹣t|=|6﹣t|,t>0且t≠6;
(3)存在点D,使得△BDP是以BP为直角边的等腰直角三角形,理由如下:
如图1,当∠PBD=90°时,过点B作GH∥x轴,过点D作DG⊥GH交于G点,过点P作PH⊥GH交于H点,
∵∠PBD=90°,
∴∠DBG+∠PBH=90°,
∵∠GBD+∠BDG=90°,
∴∠PBH=∠BDG,
∵BD=BP,
∴△BDG≌△PGH(AAS),
∴GB=PH=3,GD=BH=t﹣6,
∴D(﹣3,9﹣t),
设直线BC的解析式为y=kx+3,
∴﹣6k+3=0,
解得k=,
∴直线BC的解析式为y=x+3,
∴9﹣t=﹣+3,
解得t=;
如图2,当∠PBD=90°时,过点D作DM⊥x轴交于M点,同理可得△PDM≌△BPO(AAS),
∴DM=OP=6﹣t,MP=OB=3,
∴D(t﹣9,6﹣t),
∴6﹣t=(t﹣9)+3,
解得t=5;
综上所述:t的值为或5.
第1页(共1页)
一、选择题(每小题3分,共30分)
1.(3分)的值是( )
A.±4 B.﹣4
C.4 D.以上答案都不对
2.(3分)下列各线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.3,4,5 D.4,5,6
3.(3分)下列计算中,结果错误的是( )
A. B. C. D.
4.(3分)在下列函数中是正比例函数的是( )
A.y=3x﹣4 B.y=﹣2x+1 C.y=3x D.y=4
5.(3分)直线y=﹣5x向上平移2个单位长度,得到的直线的解析式为( )
A.y=5x+2 B.y=﹣5x+2 C.y=5x﹣2 D.y=﹣5x﹣2
6.(3分)直线y=2x+1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(3分)在下面的一组数据:2,3,2,2,2,5,4中众数是( )
A.5 B.4 C.3 D.2
8.(3分)下列性质中,矩形具有而一般的平行四边形不具有的是( )
A.对边相等 B.对角相等
C.对角线相等 D.对边平行
9.(3分)下列各点中在函数y=4x的图象上的点是( )
A.(1,2) B.(1,3) C.(1,4) D.(1,5)
10.(3分)某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20kg B.25kg C.28kg D.30kg
二、填空题(每小题3分,共30分)
11.(3分)在函数中,自变量x的取值范围是 .
12.(3分)函数y=xk﹣1+2是一次函数,则常数k的值为 .
13.(3分)在平面直角坐标系中,点M(5,﹣12)到原点的距离是 .
14.(3分)已知x,y为实数,且y=﹣+4,则+= .
15.(3分)若点A(2,y1),B(﹣1,y2)都在直线y=﹣3x+4上,则y1与y2的大小关系是 .
16.(3分)已知y与x+1成正比例,当x=1时,y=4,则当x=2时,y的值是 .
17.(3分)如图,已知△ABC为等边三角形,点E在BA的延长线上,EF⊥BC于F,交AC于D,作FH⊥AB于点H,AE=CF=2,则FH= .
18.(3分)已知菱形的两条对角线长分别是5和6,则这个菱形的面积为 .
19.(3分)在△ABC中,∠A=45°,,,则AC= .
20.(3分)如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC外一点,连接AD、CD,∠ADC=90°,CD=2AD=1,连接BD,则BD= .
三、解答题(共60分,21、22题每小题7分;23、24题每小题7分,25、26、27题每小题7分)
21.(7分)先化简,再求值:,其中x=+1.
22.(7分)如图,图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
(1)如图1,当点E为AB的中点时,请在AD上找到一点P(点P在小正方形的顶点上且不同于点F),连接EP,CP,使得△EPC为Rt△,且∠EPC=90°;
(2)请在图2中以EG为一边画矩形EGMQ(非正方形),使点M、Q均在小正方形的顶点上并直接写出矩形EGMQ的面积.
23.(8分)如图,一艘轮船以每小时35海里的速度向东航行,在A处观测到在它的东北方向(北偏东45°)点C处有一艘捕渔船,2小时后轮船到达点B处,突然收到渔船的求救信号,此时观测到渔船C位于点B的北偏东15°方向上.
(1)求∠ACB的度数;
(2)轮船收到求救信号后,立即沿BC以每小时海里的速度赶往C处救援,那么轮船需多少小时赶到C处?
24.(8分)在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=BC.
(1)求证:四边形OCEF是平行四边形;
(2)连接DF,如果DF⊥CF,请你写出图中所有的等边三角形.
25.(10分)我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,明年春季,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式;
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?请写出具体的方案.
26.(10分)在正方形ABCD中,点E在AB边上,点F在线段CE上,∠DFC=∠CEB.
(1)如图1,求证:DF=CD;
(2)如图2,连接AF,求∠AFE的度数;
(3)如图3,在(2)的条件下,延长AF,交BC边于点G,若AF=FG,AE=1,求AG的长.
27.(10分)如图,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于点A、B,直线BC与x轴负半轴交于点C,且CO=2AO.
(1)求线段AC的长;
(2)动点P从点C出发沿射线CA以每秒1个单位的速度运动,连接BP,设点P的运动时间为t(秒),△BPO的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,在线段BC上是否存在点D,连接DP,使得△BDP是以BP为直角边的等腰直角三角形,若存在,请求出t的值,若不存在,请说明理由.
2022-2023学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)的值是( )
A.±4 B.﹣4
C.4 D.以上答案都不对
【解答】解:=4.
故选:C.
2.(3分)下列各线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.3,4,5 D.4,5,6
【解答】解:∵22+32≠42,
∴A不能构成直角三角形,
∵32+42≠62,
∴B不能构成直角三角形,
∵32+42=52,
∴C能构成直角三角形,
∵42+52≠62,
∴D不能构成直角三角形,
故选:C.
3.(3分)下列计算中,结果错误的是( )
A. B. C. D.
【解答】解:A、与不属于同类二次根式,不能运算,故A符合题意;
B、5﹣2=3,故B不符合题意;
C、÷=,故C不符合题意;
D、(﹣)2=2,故D不符合题意;
故选:A.
4.(3分)在下列函数中是正比例函数的是( )
A.y=3x﹣4 B.y=﹣2x+1 C.y=3x D.y=4
【解答】解:A.y=3x﹣4为一次函数,但不是正比例函数,所以A选项不符合题意;
B.y=﹣2x+1为一次函数,但不是正比例函数,所以B选项不符合题意;
C.y=3x是正比例函数,所以C选项符合题意;
D.y=4为常函数,所以D选项不符合题意;
故选:C.
5.(3分)直线y=﹣5x向上平移2个单位长度,得到的直线的解析式为( )
A.y=5x+2 B.y=﹣5x+2 C.y=5x﹣2 D.y=﹣5x﹣2
【解答】解:将直线y=﹣5x向上平移2个单位长度,得到的直线的解析式为:y=﹣5x+2.
故选:B.
6.(3分)直线y=2x+1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵y=2x﹣1,k=2>0,b=1,
∴该函数经过第一、三、二象限,不经过第四象限,
故选:D.
7.(3分)在下面的一组数据:2,3,2,2,2,5,4中众数是( )
A.5 B.4 C.3 D.2
【解答】解:这组数据的众数为2,
故选:D.
8.(3分)下列性质中,矩形具有而一般的平行四边形不具有的是( )
A.对边相等 B.对角相等
C.对角线相等 D.对边平行
【解答】解:矩形的特性是:四个角都是直角,对角线相等.
故选:C.
9.(3分)下列各点中在函数y=4x的图象上的点是( )
A.(1,2) B.(1,3) C.(1,4) D.(1,5)
【解答】解:当x=1时,y=4×1=4,4≠2,
∴点(1,4)在函数y=4x的图象上.
故选:C.
10.(3分)某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20kg B.25kg C.28kg D.30kg
【解答】解:设y与x的函数关系式为y=kx+b,
由题意可知,
解得,
所以函数关系式为y=30x﹣600,
当y=0时,即30x﹣600=0,所以x=20.
故选:A.
二、填空题(每小题3分,共30分)
11.(3分)在函数中,自变量x的取值范围是 x≤2 .
【解答】解:由题意,得
2﹣x≥0,解得x≤2,
故答案为:x≤2.
12.(3分)函数y=xk﹣1+2是一次函数,则常数k的值为 2 .
【解答】解:∵函数y=xk﹣1+2是一次函数,
∴k﹣1=1,
∴k=2,
故答案为:2.
13.(3分)在平面直角坐标系中,点M(5,﹣12)到原点的距离是 13 .
【解答】解:由勾股定理得,点M(5,﹣12)到原点的距离为,
故答案为:13.
14.(3分)已知x,y为实数,且y=﹣+4,则+= 5 .
【解答】解:依题意得:,
解得x=9,
所以y=4
故+=3+2=5.
故答案为:5.
15.(3分)若点A(2,y1),B(﹣1,y2)都在直线y=﹣3x+4上,则y1与y2的大小关系是 y1<y2 .
【解答】解:∵k=﹣3<0,
∴y随x的增大而减小,
又∵点A(2,y1),B(﹣1,y2)都在直线y=﹣3x+4上,且2>﹣1,
∴y1<y2.
故答案为:y1<y2.
16.(3分)已知y与x+1成正比例,当x=1时,y=4,则当x=2时,y的值是 6 .
【解答】解:设y=k(x+1)(k≠0),
把x=1,y=4代入,得k(1+1)=4.
解得k=2.
所以当x=2时,y=2(2+1)=6.
故答案为:6.
17.(3分)如图,已知△ABC为等边三角形,点E在BA的延长线上,EF⊥BC于F,交AC于D,作FH⊥AB于点H,AE=CF=2,则FH= 3 .
【解答】解:∵△ABC为等边三角形,
∴∠C=∠B=∠CAB=60°,
∵EF⊥BC,
∴∠DFC=90°,
∵CF=4,
∴CD=2CF=8,∠CDF=30°,
∴∠ADE=30°,
∴∠E=∠CAB﹣∠ADE=30°,
∴EA=AD=2,
∴AC=10,
∴BF=6,
∴BH=3,
∴FH==3,
故答案为:3.
18.(3分)已知菱形的两条对角线长分别是5和6,则这个菱形的面积为 15 .
【解答】解:∵菱形的两条对角线长分别是5和6,
∴这个菱形的面积为5×6÷2=15.
故答案为:15.
19.(3分)在△ABC中,∠A=45°,,,则AC= 5或3 .
【解答】解:过B作BH⊥AC于H,
①当H在边AC上时,如图:
∵∠A=45°,BH⊥AC,
∴△ABH是等腰直角三角形,
∴AH=BH==4,
在Rt△BHC中,
CH===1,
∴AC=AH+CH=4+1=5;
②当H在边AC延长线上时,如图:
同理可得AH=BH=4,CH=1,
∴AC=AH﹣CH=3;
综上所述,AC的长为5或3;
故答案为:5或3.
20.(3分)如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC外一点,连接AD、CD,∠ADC=90°,CD=2AD=1,连接BD,则BD= .
【解答】解:延长AD交BC的延长线于E,过点D作DF⊥CE于点F,
∵CD=2AD=1,∠ADC=90°,
∴AC==,
设DE=a,
∴,
解得a=2,
∴DE=2,
∴CE==,
∵DE,
∴,
∴CF==,
∵CB=AC=,
∴BF=BC+CF=,
∴BD==.
故答案为:.
三、解答题(共60分,21、22题每小题7分;23、24题每小题7分,25、26、27题每小题7分)
21.(7分)先化简,再求值:,其中x=+1.
【解答】解:原式=
=
=.
当x=+1时,原式=.
22.(7分)如图,图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
(1)如图1,当点E为AB的中点时,请在AD上找到一点P(点P在小正方形的顶点上且不同于点F),连接EP,CP,使得△EPC为Rt△,且∠EPC=90°;
(2)请在图2中以EG为一边画矩形EGMQ(非正方形),使点M、Q均在小正方形的顶点上并直接写出矩形EGMQ的面积.
【解答】解:(1)如图1,△EPC即为所求;
(2)如图2,矩形EGMQ即为所求;
矩形EGMQ面积=EG EQ=×=10.
23.(8分)如图,一艘轮船以每小时35海里的速度向东航行,在A处观测到在它的东北方向(北偏东45°)点C处有一艘捕渔船,2小时后轮船到达点B处,突然收到渔船的求救信号,此时观测到渔船C位于点B的北偏东15°方向上.
(1)求∠ACB的度数;
(2)轮船收到求救信号后,立即沿BC以每小时海里的速度赶往C处救援,那么轮船需多少小时赶到C处?
【解答】解:(1)∵∠DAC=45°,∠DAB=90°,
∴∠CAB=45°,
∵∠EBC=15°,∠ABE=90°,
∴∠ABC=105°,
∴∠ACB=180°﹣∠ABC﹣∠CAB=180°﹣105°﹣45°=30°;
(2)过B作BF⊥AC于F,
∴∠FAB=∠FBA=45°,
∴AF=BF,
∵AB=35×2=70(海里),AB2=AF2+BF2,
∴(海里),
∵∠ACB=30°,
∴(海里),
∵,
∴轮船需小时赶到C处.
24.(8分)在菱形ABCD中,点O是对角线的交点,E点是边CD的中点,点F在BC延长线上,且CF=BC.
(1)求证:四边形OCEF是平行四边形;
(2)连接DF,如果DF⊥CF,请你写出图中所有的等边三角形.
【解答】(1)证明:∵四边形ABCD是菱形,
∴BO=DO,
∵E点是边CD的中点,
∴OE是△BDC的中位线,
∴OE∥BC且OE=BC,
∵CF=BC,
∴OE=CF,
∵OE∥CF,
∴四边形OCFE是平行四边形;
(2)解:∵DF⊥CF,E点是边CD的中点,
∴EF=,
∵CE=,
CF==CD,
∴△ECF为等边三角形;
∵四边形OCFE是平行四边形,
∴OC=EF=CE=CF=OE,
∴△OCE为等边三角形;
∵△ECF为等边三角形,
∴∠ECF=60°,
∴∠ABC=60°,
∵四边形ABCD是菱形,
∴△ABC为等边三角形;
同理得△ADC为等边三角形;
∴图中的等边三角形有:△OCE,△ECF,△ABC,△ADC
25.(10分)我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,明年春季,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式;
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?请写出具体的方案.
【解答】解:(1)由题意y=x+1.5×2x+2(100﹣3x)=﹣2x+200,
所以总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式为y=x+1.5×2x+2(100﹣3x)=﹣2x+200.
(2)由题意﹣2x+200≥180,
解得x≤10,
∵x≥8,
∴8≤x≤10.
∵x为整数,
∴x=8,9,10.
∴有3种种植方案,
方案一:种植西红柿8公顷、马铃薯76公顷、青椒16公顷.
方案二:种植西红柿9公顷、马铃薯73公顷、青椒18公顷.
方案三:种植西红柿10公顷、马铃薯70公顷、青椒20公顷.
26.(10分)在正方形ABCD中,点E在AB边上,点F在线段CE上,∠DFC=∠CEB.
(1)如图1,求证:DF=CD;
(2)如图2,连接AF,求∠AFE的度数;
(3)如图3,在(2)的条件下,延长AF,交BC边于点G,若AF=FG,AE=1,求AG的长.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,
∴∠CEB+∠BCE=90°,∠BCE+∠DCF=90°,
∴∠CEB=∠DCF,
∵∠DFC=∠CEB,
∴∠DFC=∠DCF,
∴DF=CD;
(2)解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
由(1)得DF=CD,
∴AD=DF=CD,
∴∠DAF=∠DFA,∠DFC=∠DCF,
在四边形ADCF中,∠DAF+∠AFC+∠DCF=360°﹣∠ADC=360°﹣90°=270°,
∴∠DAF+∠DFA+∠DFC+∠DCF=270°,
∴2∠DFA+2∠DFC=2∠AFC=270°,
∴∠AFC=135°,
∴∠AFE=180°﹣∠AFC=180°﹣135°=45°;
(3)解:如图3,延长CE交DA延长线于点H,过G作GK⊥CF于点K,
则∠CKG=∠FKG=90°,
∵四边形ABCD是正方形,
∴∠ADC=∠BAD=90°,AD∥BC,
∴∠H=∠FCG,∠HAF=∠CGF,
∵AF=FG,
∴△AFH≌△GFC(AAS),
∴AH=CG,FH=CF,
∵∠ADC=90°,
∴DF=CF,
由(1)得:DF=CD,
∴DF=CF=CD,
∴△DCF是等边三角形,
∴∠DCH=60°,
∴∠H=∠HCG=90°﹣60°=30°,
∠HAE=180°﹣90°=90°,
在Rt△AHE中,EH=2AE=2,
由勾股定理得:AH===,
∴CG=AH=,
在Rt△CGK中,KG=CG=×=,
在Rt△FKG中,∠KFG=∠AFE=45°,
∴△FKG是等腰直角三角形,
∴FK=KG=,
由勾股定理得:FG===,
∴AG=2FG=2×=.
27.(10分)如图,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于点A、B,直线BC与x轴负半轴交于点C,且CO=2AO.
(1)求线段AC的长;
(2)动点P从点C出发沿射线CA以每秒1个单位的速度运动,连接BP,设点P的运动时间为t(秒),△BPO的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,在线段BC上是否存在点D,连接DP,使得△BDP是以BP为直角边的等腰直角三角形,若存在,请求出t的值,若不存在,请说明理由.
【解答】解:(1)把x=0代入y=﹣x+3,y=3,
∴B(0,3),
把y=0代入y=﹣x+3,x=3,
∴A(3,0),
∴AO=3,
∵CO=2AO,
∴CO=6,
∴C(﹣6,0);
∴AC=6+3=9;
(2)∵C(﹣6,0),动点P从点C出发沿射线CA以每秒1个单位的速度运动,
∴CP=t,
∴P(﹣6+t,0),
∴OP=|6﹣t|,
∴S=×3×|6﹣t|=|6﹣t|,t>0且t≠6;
(3)存在点D,使得△BDP是以BP为直角边的等腰直角三角形,理由如下:
如图1,当∠PBD=90°时,过点B作GH∥x轴,过点D作DG⊥GH交于G点,过点P作PH⊥GH交于H点,
∵∠PBD=90°,
∴∠DBG+∠PBH=90°,
∵∠GBD+∠BDG=90°,
∴∠PBH=∠BDG,
∵BD=BP,
∴△BDG≌△PGH(AAS),
∴GB=PH=3,GD=BH=t﹣6,
∴D(﹣3,9﹣t),
设直线BC的解析式为y=kx+3,
∴﹣6k+3=0,
解得k=,
∴直线BC的解析式为y=x+3,
∴9﹣t=﹣+3,
解得t=;
如图2,当∠PBD=90°时,过点D作DM⊥x轴交于M点,同理可得△PDM≌△BPO(AAS),
∴DM=OP=6﹣t,MP=OB=3,
∴D(t﹣9,6﹣t),
∴6﹣t=(t﹣9)+3,
解得t=5;
综上所述:t的值为或5.
第1页(共1页)
同课章节目录
