黑龙江省哈尔滨市南岗区萧红中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市南岗区萧红中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 850.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 09:56:31 | ||
图片预览


文档简介
2023-2024学年黑龙江省哈尔滨市南岗区萧红中学九年级(上)开学数学试卷(五四学制)
一、选择题:(每小题3分,共计36分)
1.(3分)﹣3的倒数是( )
A.3 B. C.﹣ D.﹣3
2.(3分)下列四个汽车标志图中,不是轴对称图形的是( )
A. B.
C. D.
3.(3分)下列运算正确的是( )
A.x3 x2=x6 B.x6÷x2=x3 C.x3+x3=2x3 D.(x2)3=x5
4.(3分)一组数据﹣1,5,5,1,3,4,5的众数、中位数分别为( )
A.5、4 B.5、5 C.5、3 D.5、1
5.(3分)如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A的仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
A.20tan37° B. C. D.20sin37°
6.(3分)方程=0的解是( )
A.﹣1 B.2 C.5 D.无解
7.(3分)某果园2012年水果产量为100吨,2014年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
A.144(1﹣x)2=100 B.100(1﹣x)2=144
C.144(1+x)2=100 D.100(1+x)2=144
8.(3分)如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(﹣2,﹣2),(2,﹣2),则顶点D的坐标是( )
A.(﹣4,﹣1) B.(4,﹣2) C.(4,1) D.(2,1)
9.(3分)在平行四边形ABCD中,已知∠A:∠B=1:2,则∠B的度数是( )
A.45° B.90° C.120° D.135°
10.(3分)如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,则下列结论中一定正确的是( )
A.= B.= C.= D.=
11.(3分)受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水21吨,则应交水费( )
A.52.5元 B.45元 C.42元 D.37.8元
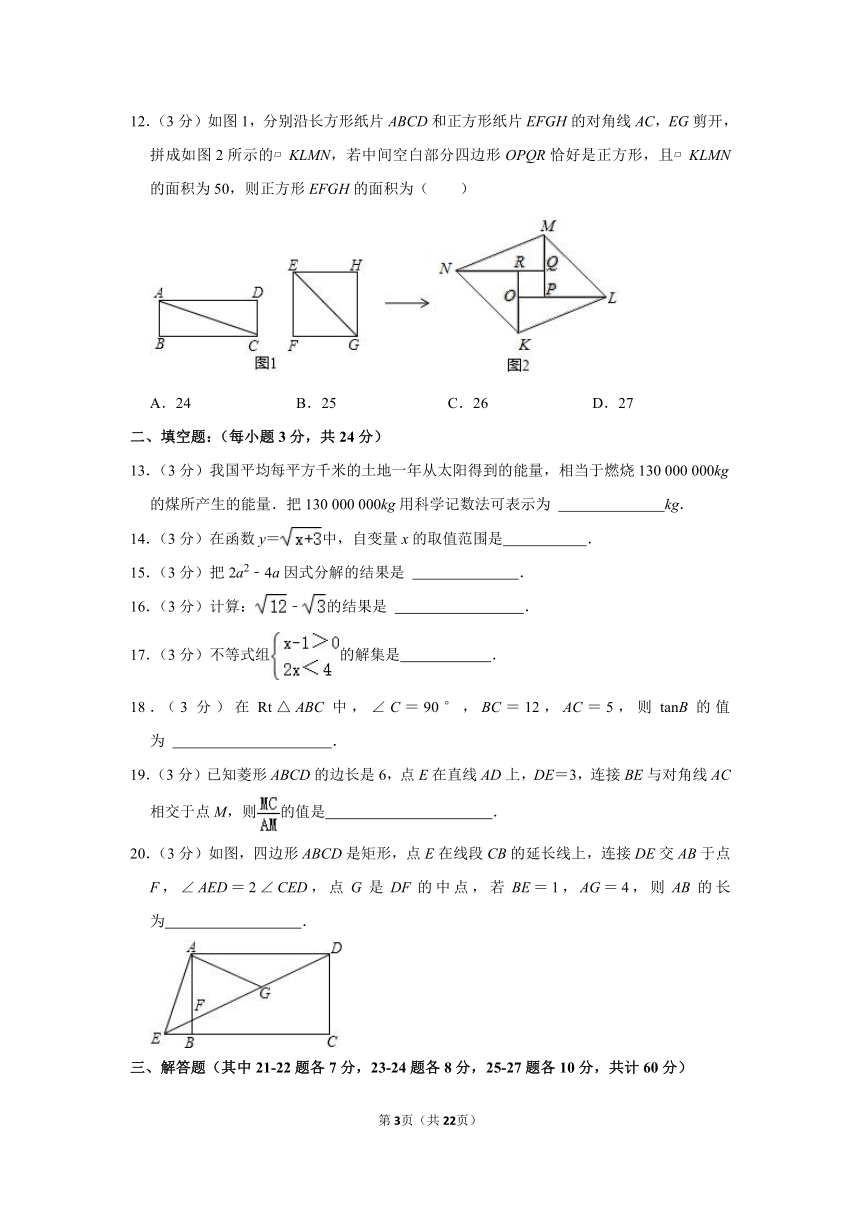
12.(3分)如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的 KLMN,若中间空白部分四边形OPQR恰好是正方形,且 KLMN的面积为50,则正方形EFGH的面积为( )
A.24 B.25 C.26 D.27
二、填空题:(每小题3分,共24分)
13.(3分)我国平均每平方千米的土地一年从太阳得到的能量,相当于燃烧130 000 000kg的煤所产生的能量.把130 000 000kg用科学记数法可表示为 kg.
14.(3分)在函数y=中,自变量x的取值范围是 .
15.(3分)把2a2﹣4a因式分解的结果是 .
16.(3分)计算:﹣的结果是 .
17.(3分)不等式组的解集是 .
18.(3分)在Rt△ABC中,∠C=90°,BC=12,AC=5,则tanB的值为 .
19.(3分)已知菱形ABCD的边长是6,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则的值是 .
20.(3分)如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
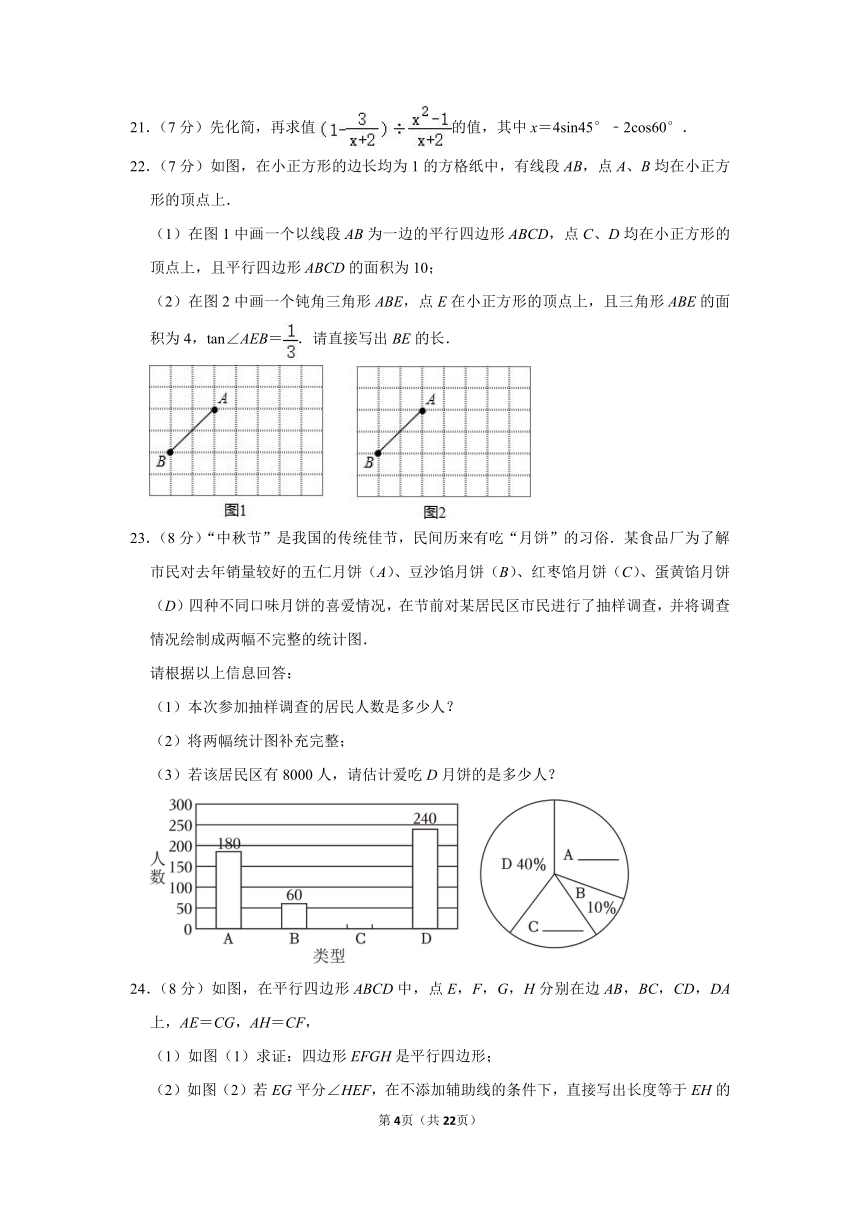
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
22.(7分)如图,在小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
(1)在图1中画一个以线段AB为一边的平行四边形ABCD,点C、D均在小正方形的顶点上,且平行四边形ABCD的面积为10;
(2)在图2中画一个钝角三角形ABE,点E在小正方形的顶点上,且三角形ABE的面积为4,tan∠AEB=.请直接写出BE的长.
23.(8分)“中秋节”是我国的传统佳节,民间历来有吃“月饼”的习俗.某食品厂为了解市民对去年销量较好的五仁月饼(A)、豆沙馅月饼(B)、红枣馅月饼(C)、蛋黄馅月饼(D)四种不同口味月饼的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成两幅不完整的统计图.
请根据以上信息回答:
(1)本次参加抽样调查的居民人数是多少人?
(2)将两幅统计图补充完整;
(3)若该居民区有8000人,请估计爱吃D月饼的是多少人?
24.(8分)如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,
(1)如图(1)求证:四边形EFGH是平行四边形;
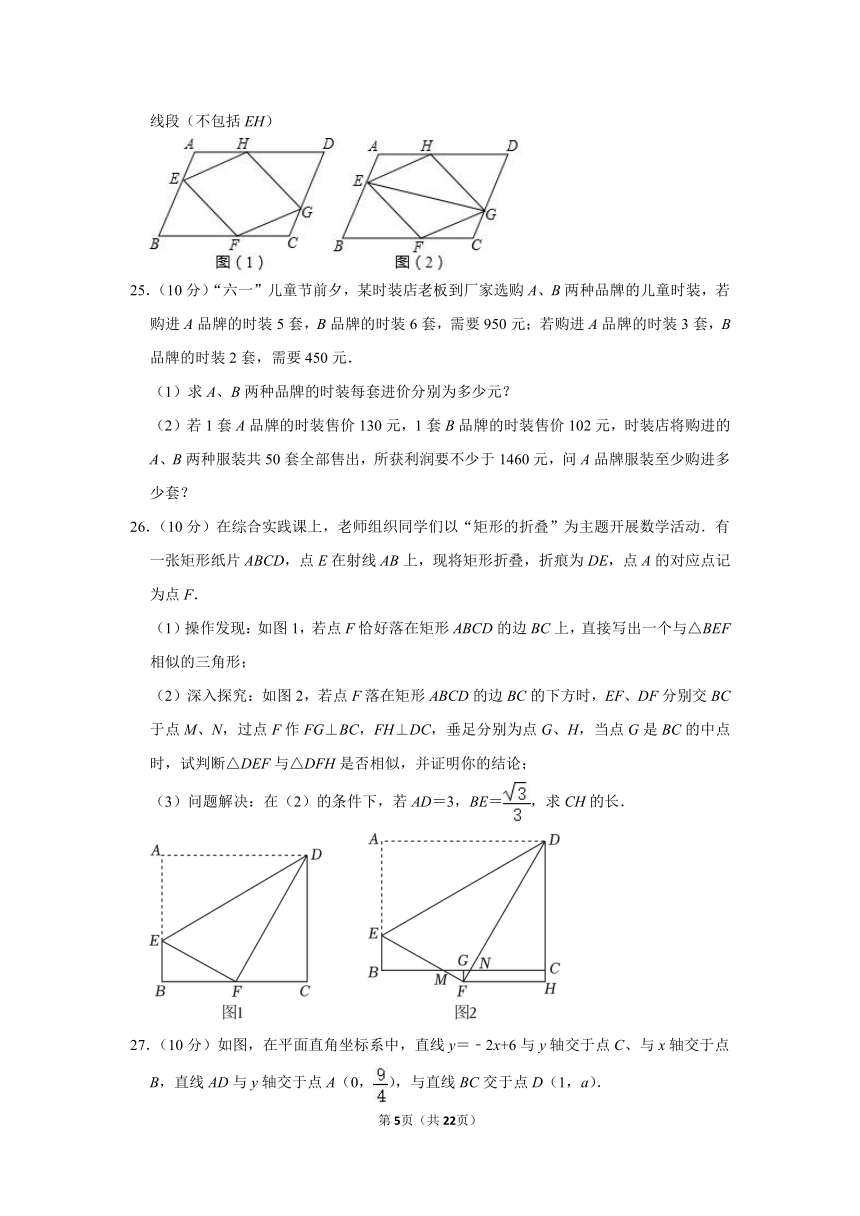
(2)如图(2)若EG平分∠HEF,在不添加辅助线的条件下,直接写出长度等于EH的线段(不包括EH)
25.(10分)“六一”儿童节前夕,某时装店老板到厂家选购A、B两种品牌的儿童时装,若购进A品牌的时装5套,B品牌的时装6套,需要950元;若购进A品牌的时装3套,B品牌的时装2套,需要450元.
(1)求A、B两种品牌的时装每套进价分别为多少元?
(2)若1套A品牌的时装售价130元,1套B品牌的时装售价102元,时装店将购进的A、B两种服装共50套全部售出,所获利润要不少于1460元,问A品牌服装至少购进多少套?
26.(10分)在综合实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD,点E在射线AB上,现将矩形折叠,折痕为DE,点A的对应点记为点F.
(1)操作发现:如图1,若点F恰好落在矩形ABCD的边BC上,直接写出一个与△BEF相似的三角形;
(2)深入探究:如图2,若点F落在矩形ABCD的边BC的下方时,EF、DF分别交BC于点M、N,过点F作FG⊥BC,FH⊥DC,垂足分别为点G、H,当点G是BC的中点时,试判断△DEF与△DFH是否相似,并证明你的结论;
(3)问题解决:在(2)的条件下,若AD=3,BE=,求CH的长.
27.(10分)如图,在平面直角坐标系中,直线y=﹣2x+6与y轴交于点C、与x轴交于点B,直线AD与y轴交于点A(0,),与直线BC交于点D(1,a).
(1)如图(1)求直线AD的解析式;
(2)如图(2)点P是直线BC上的一点,点P的横坐标是t,求△OCP的面积S与t的函数关系式;
(3)如图(3)在(2)的条件下,将射线CB绕着点C顺时针旋转45°与射线DA交于点Q,当点P在线段DB上,连接PQ,若∠CQP=∠OCB,求点P的坐标.
2023-2024学年黑龙江省哈尔滨市南岗区萧红中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题:(每小题3分,共计36分)
1.(3分)﹣3的倒数是( )
A.3 B. C.﹣ D.﹣3
【解答】解:∵﹣3×(﹣)=1,
∴﹣3的倒数是﹣.
故选:C.
2.(3分)下列四个汽车标志图中,不是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形,故错误;
B、不是轴对称图形,故正确;
C、是轴对称图形,故错误;
D、是轴对称图形,故错误.
故选:B.
3.(3分)下列运算正确的是( )
A.x3 x2=x6 B.x6÷x2=x3 C.x3+x3=2x3 D.(x2)3=x5
【解答】解:A、x3 x2=x5,选项A不正确,不符合题意;
B、x6÷x2=x4,选项B不正确,不符合题意;
C、x3+x3=2x3,选项C正确,符合题意;
D、(x2)3=x6,选项D不正确,不符合题意.
故选:C.
4.(3分)一组数据﹣1,5,5,1,3,4,5的众数、中位数分别为( )
A.5、4 B.5、5 C.5、3 D.5、1
【解答】解:数据从小到大排列为:﹣1,1,3,4,5,5,5,
所以中位数为4,
数据5出现了3次,最多,
所以这组数据的众数为5.
故选:A.
5.(3分)如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A的仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
A.20tan37° B. C. D.20sin37°
【解答】解:如图,在直角△ABC中,∠B=90°,∠C=37°,BC=20m,
∴tanC=,
则AB=BC tanC=20tan37°.
故选:A.
6.(3分)方程=0的解是( )
A.﹣1 B.2 C.5 D.无解
【解答】解:分式方程+=0,
去分母得:x﹣2+3=0,
解得:x=﹣1,
经检验x=﹣1是分式方程的解.
故选:A.
7.(3分)某果园2012年水果产量为100吨,2014年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
A.144(1﹣x)2=100 B.100(1﹣x)2=144
C.144(1+x)2=100 D.100(1+x)2=144
【解答】解:设该果园水果产量的年平均增长率为x,则2013年的产量为100(1+x)吨,2014年的产量为100(1+x)(1+x)=100(1+x)2吨,
根据题意,得100(1+x)2=144,
故选:D.
8.(3分)如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(﹣2,﹣2),(2,﹣2),则顶点D的坐标是( )
A.(﹣4,﹣1) B.(4,﹣2) C.(4,1) D.(2,1)
【解答】解:∵平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(﹣2,﹣2),(2,﹣2),
∴AD=BC=2﹣(﹣2)=4,
∵BC∥x轴,AD∥BC,
∴AD∥x轴,
∴D(4,1),
故选:C.
9.(3分)在平行四边形ABCD中,已知∠A:∠B=1:2,则∠B的度数是( )
A.45° B.90° C.120° D.135°
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A:∠B=1:2,
∴∠B=180°×=120°.
故选:C.
10.(3分)如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,则下列结论中一定正确的是( )
A.= B.= C.= D.=
【解答】解:∵AD∥BE∥CF,
∴,故A错误;
,故C错误;
,故D正确.
故选:D.
11.(3分)受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水21吨,则应交水费( )
A.52.5元 B.45元 C.42元 D.37.8元
【解答】解:设直线AB解析式为y=kx+b,把(15,27)(20,39.5)代入得:,
解之得:即y=2.5x﹣10.5,当x=21时,y=42.
故选:C.
12.(3分)如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的 KLMN,若中间空白部分四边形OPQR恰好是正方形,且 KLMN的面积为50,则正方形EFGH的面积为( )
A.24 B.25 C.26 D.27
【解答】解:如图,设PM=PL=NR=KR=a,正方形ORQP的边长为b.
由题意:a2+b2+(a+b)(a﹣b)=50,
∴a2=25,
∴正方形EFGH的面积=a2=25,
故选:B.
二、填空题:(每小题3分,共24分)
13.(3分)我国平均每平方千米的土地一年从太阳得到的能量,相当于燃烧130 000 000kg的煤所产生的能量.把130 000 000kg用科学记数法可表示为 1.3×108 kg.
【解答】解:130 000 000=1.3×108,
故答案为:1.3×108.
14.(3分)在函数y=中,自变量x的取值范围是 x≥﹣3 .
【解答】解:根据题意得:x+3≥0,解得:x≥﹣3.
故答案为:x≥﹣3.
15.(3分)把2a2﹣4a因式分解的结果是 2a(a﹣2) .
【解答】解:原式=2a(a﹣2),
故答案为:2a(a﹣2).
16.(3分)计算:﹣的结果是 .
【解答】解:=2﹣=.
故答案为:.
17.(3分)不等式组的解集是 1<x<2 .
【解答】解:,
∵解不等式①得:x>1,
解不等式②得:x<2,
∴不等式组的解集为1<x<2,
故答案为:1<x<2;
18.(3分)在Rt△ABC中,∠C=90°,BC=12,AC=5,则tanB的值为 .
【解答】解:在Rt△ABC中,∠C=90°,
∴tanB==.
故答案为.
故答案为:.
19.(3分)已知菱形ABCD的边长是6,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则的值是 2或 .
【解答】解:分两种情况:
(1)点E在线段AD上时,△AEM∽△CBM,∴=2;
(2)点E在线段AD的延长线上时,△AME∽△CMB,∴=.
20.(3分)如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为 .
【解答】解:∵四边形ABCD是矩形,点G是DF的中点,
∴AG=DG,
∴∠ADG=∠DAG,
∵AD∥BC,
∴∠ADG=∠CED,
∴∠AGE=∠ADG+∠DAG=2∠CED,
∵∠AED=2∠CED,
∴∠AED=∠AGE,
∴AE=AG=4,
在Rt△ABE中,AB===.
故答案为:.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
【解答】解:原式=
=
=,
x=4sin45°﹣2cos60°
=4×﹣2×
=,
∴当x=时,原式====.
22.(7分)如图,在小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
(1)在图1中画一个以线段AB为一边的平行四边形ABCD,点C、D均在小正方形的顶点上,且平行四边形ABCD的面积为10;
(2)在图2中画一个钝角三角形ABE,点E在小正方形的顶点上,且三角形ABE的面积为4,tan∠AEB=.请直接写出BE的长.
【解答】解:(1)如图1所示;
(2)如图2所示;
BE==2.
23.(8分)“中秋节”是我国的传统佳节,民间历来有吃“月饼”的习俗.某食品厂为了解市民对去年销量较好的五仁月饼(A)、豆沙馅月饼(B)、红枣馅月饼(C)、蛋黄馅月饼(D)四种不同口味月饼的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成两幅不完整的统计图.
请根据以上信息回答:
(1)本次参加抽样调查的居民人数是多少人?
(2)将两幅统计图补充完整;
(3)若该居民区有8000人,请估计爱吃D月饼的是多少人?
【解答】解:(1)本次参加抽样调查的居民的人数是:60÷10%=600(人);
(2)C类的人数是:600﹣180﹣60﹣240=120(人),所占的百分比是:×100%=20%,
A类所占的百分比是:×100%=30%.
A 类所占的百分比是:1﹣10%﹣20%﹣40%=30%.补图
(3))8000×40%=3200(人).
答:估计爱吃D 月饼的人数为3200人.
24.(8分)如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,
(1)如图(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若EG平分∠HEF,在不添加辅助线的条件下,直接写出长度等于EH的线段(不包括EH)
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,且AE=CG,AH=CF
∴△AEH≌△CGF(SAS),
∴EH=GF,
同理EF=GH
∴四边形EFGH是平行四边形
(2)∵四边形EFGH是平行四边形
∴EH∥FG
∴∠HEG=∠EGF
∵EG平分∠HEF
∴∠HEG=∠FEG
∴∠EGF=∠FEG
∴EF=FG,且四边形EFGH是平行四边形
∴四边形EFGH是菱形
∴EH=EF=FG=GH
25.(10分)“六一”儿童节前夕,某时装店老板到厂家选购A、B两种品牌的儿童时装,若购进A品牌的时装5套,B品牌的时装6套,需要950元;若购进A品牌的时装3套,B品牌的时装2套,需要450元.
(1)求A、B两种品牌的时装每套进价分别为多少元?
(2)若1套A品牌的时装售价130元,1套B品牌的时装售价102元,时装店将购进的A、B两种服装共50套全部售出,所获利润要不少于1460元,问A品牌服装至少购进多少套?
【解答】解:(1)设A种品牌的时装每套进价为x元,B种品牌的时装每套进价为y元,依题意有
,
解得.
故A种品牌的时装每套进价为100元,B种品牌的时装每套进价为75元;
(2)设A种品牌的时装购进m套,则B种品牌的时装购进(50﹣m)套,依题意有
(130﹣100)m+(102﹣75)(50﹣m)≥1460,
解得m≥36,
∵m为正整数,
∴A品牌服装至少购进37套.
26.(10分)在综合实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD,点E在射线AB上,现将矩形折叠,折痕为DE,点A的对应点记为点F.
(1)操作发现:如图1,若点F恰好落在矩形ABCD的边BC上,直接写出一个与△BEF相似的三角形;
(2)深入探究:如图2,若点F落在矩形ABCD的边BC的下方时,EF、DF分别交BC于点M、N,过点F作FG⊥BC,FH⊥DC,垂足分别为点G、H,当点G是BC的中点时,试判断△DEF与△DFH是否相似,并证明你的结论;
(3)问题解决:在(2)的条件下,若AD=3,BE=,求CH的长.
【解答】解:(1)△CFD与△BEF相似的三角形,
∵四边形ABCD是矩形,
∴∠B=∠C=∠A=90°,
∴∠BFE+∠BEF=90°,
由折叠的性质可知,∠DFE=∠A=90°,
∴∠BFE+∠CFD=90°,
∴∠BEF=∠CFD,
∴△BEF∽△CFD;
(2)△DEF∽△DFH,
理由:如解图,分别延长HF,AB交于点P,
∵四边形ABCD是矩形,
∴∠ABC=∠ADC=90°,
∵FH⊥CD,
∴∠DHF=90°,
∴四边形 BPFG、四边形GFHC、四边形APHD都是矩形,
∴∠P=∠H=∠A=90°,
∴∠PFE+∠PEF=90°,
由折叠的性质可知,∠DFE=∠A=90°,
∴∠PFE+∠HFD=90°,
∴∠PEF=∠HFD,
∴△PEF∽△HFD,
∴,
∵BG=MP,CG=FH,点G是BG的中点,
∴BG=CG,
∴PF=FH,
∴,
∵∠DFE=∠H=90°,
∴△DEF∽△DFH;
(3)∵由(2)可知,△DEF∽△DFH,
∴∠EDF=∠FDH,
由折叠的性质可知,∠EDF=∠ADE,DF=AD=3,
∴∠ADE=∠EDF=∠FDH=30°,
DH=DF cos30°=,
①当点E在AB上时,如解图,
AE=AD=×3=,
∴AB=AE+BE=+=,
∴CH=DH﹣CD=DH﹣AB=﹣=,
②当点E在AB的延长线上时,如解图,
AE=AD=×3=,
∴AB=AE﹣BE=﹣=,
∴CH=DH﹣CD=DH﹣AB=﹣=,
综上所述,CH的长为:或.
27.(10分)如图,在平面直角坐标系中,直线y=﹣2x+6与y轴交于点C、与x轴交于点B,直线AD与y轴交于点A(0,),与直线BC交于点D(1,a).
(1)如图(1)求直线AD的解析式;
(2)如图(2)点P是直线BC上的一点,点P的横坐标是t,求△OCP的面积S与t的函数关系式;
(3)如图(3)在(2)的条件下,将射线CB绕着点C顺时针旋转45°与射线DA交于点Q,当点P在线段DB上,连接PQ,若∠CQP=∠OCB,求点P的坐标.
【解答】解:(1)把点D(1,a)代入y=﹣2x+6,得:
∴a=﹣2×1+6=4,
∴点D的坐标为(1,4),
设直线AD解析式为y=kx+b,把点D(1,4)、A(0,)代入y=kx+b,
得:,
∴,
∴直线AD解析式为y=x+,
(2)过P点作PH⊥y轴,
y=﹣2x+6 当x=0 时,y=6,
∴C(0,6),
∴OC=6,
当P点在y轴右侧时,
当t>0,
∴△OCP的面积S=OC PH=×6×t=3t,
当P点在y轴左侧时,当t<0时,
∴△OCP的面积S=OC PH=×6×(﹣t)=﹣3t,
即S与t的函数关系式为:S=3t(t>0)或S=﹣3t(t<0);
(3)如图,过点B作BE⊥BC,交直线CQ于E,过E作EF⊥x轴于F,
在△OBC和△FEB中,
,
∴△OBC≌△FEB(ASA),
∴E(﹣3,﹣3),C(0,6),
∴直线CQ解析式可求为:y=3x+6,
,
解得,
∴Q(﹣3,﹣3),
∴点 Q与点E重合,
过点Q作QM⊥y轴,过P作PH⊥x轴,
PH=﹣2t+6,QM=3,
∵∠CQP=∠OCB,
∴△POH为等腰直角三角形,
∴﹣2t+6=t.
∴t=2.
∴P(2,2).
第1页(共1页)
一、选择题:(每小题3分,共计36分)
1.(3分)﹣3的倒数是( )
A.3 B. C.﹣ D.﹣3
2.(3分)下列四个汽车标志图中,不是轴对称图形的是( )
A. B.
C. D.
3.(3分)下列运算正确的是( )
A.x3 x2=x6 B.x6÷x2=x3 C.x3+x3=2x3 D.(x2)3=x5
4.(3分)一组数据﹣1,5,5,1,3,4,5的众数、中位数分别为( )
A.5、4 B.5、5 C.5、3 D.5、1
5.(3分)如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A的仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
A.20tan37° B. C. D.20sin37°
6.(3分)方程=0的解是( )
A.﹣1 B.2 C.5 D.无解
7.(3分)某果园2012年水果产量为100吨,2014年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
A.144(1﹣x)2=100 B.100(1﹣x)2=144
C.144(1+x)2=100 D.100(1+x)2=144
8.(3分)如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(﹣2,﹣2),(2,﹣2),则顶点D的坐标是( )
A.(﹣4,﹣1) B.(4,﹣2) C.(4,1) D.(2,1)
9.(3分)在平行四边形ABCD中,已知∠A:∠B=1:2,则∠B的度数是( )
A.45° B.90° C.120° D.135°
10.(3分)如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,则下列结论中一定正确的是( )
A.= B.= C.= D.=
11.(3分)受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水21吨,则应交水费( )
A.52.5元 B.45元 C.42元 D.37.8元
12.(3分)如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的 KLMN,若中间空白部分四边形OPQR恰好是正方形,且 KLMN的面积为50,则正方形EFGH的面积为( )
A.24 B.25 C.26 D.27
二、填空题:(每小题3分,共24分)
13.(3分)我国平均每平方千米的土地一年从太阳得到的能量,相当于燃烧130 000 000kg的煤所产生的能量.把130 000 000kg用科学记数法可表示为 kg.
14.(3分)在函数y=中,自变量x的取值范围是 .
15.(3分)把2a2﹣4a因式分解的结果是 .
16.(3分)计算:﹣的结果是 .
17.(3分)不等式组的解集是 .
18.(3分)在Rt△ABC中,∠C=90°,BC=12,AC=5,则tanB的值为 .
19.(3分)已知菱形ABCD的边长是6,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则的值是 .
20.(3分)如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
22.(7分)如图,在小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
(1)在图1中画一个以线段AB为一边的平行四边形ABCD,点C、D均在小正方形的顶点上,且平行四边形ABCD的面积为10;
(2)在图2中画一个钝角三角形ABE,点E在小正方形的顶点上,且三角形ABE的面积为4,tan∠AEB=.请直接写出BE的长.
23.(8分)“中秋节”是我国的传统佳节,民间历来有吃“月饼”的习俗.某食品厂为了解市民对去年销量较好的五仁月饼(A)、豆沙馅月饼(B)、红枣馅月饼(C)、蛋黄馅月饼(D)四种不同口味月饼的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成两幅不完整的统计图.
请根据以上信息回答:
(1)本次参加抽样调查的居民人数是多少人?
(2)将两幅统计图补充完整;
(3)若该居民区有8000人,请估计爱吃D月饼的是多少人?
24.(8分)如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,
(1)如图(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若EG平分∠HEF,在不添加辅助线的条件下,直接写出长度等于EH的线段(不包括EH)
25.(10分)“六一”儿童节前夕,某时装店老板到厂家选购A、B两种品牌的儿童时装,若购进A品牌的时装5套,B品牌的时装6套,需要950元;若购进A品牌的时装3套,B品牌的时装2套,需要450元.
(1)求A、B两种品牌的时装每套进价分别为多少元?
(2)若1套A品牌的时装售价130元,1套B品牌的时装售价102元,时装店将购进的A、B两种服装共50套全部售出,所获利润要不少于1460元,问A品牌服装至少购进多少套?
26.(10分)在综合实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD,点E在射线AB上,现将矩形折叠,折痕为DE,点A的对应点记为点F.
(1)操作发现:如图1,若点F恰好落在矩形ABCD的边BC上,直接写出一个与△BEF相似的三角形;
(2)深入探究:如图2,若点F落在矩形ABCD的边BC的下方时,EF、DF分别交BC于点M、N,过点F作FG⊥BC,FH⊥DC,垂足分别为点G、H,当点G是BC的中点时,试判断△DEF与△DFH是否相似,并证明你的结论;
(3)问题解决:在(2)的条件下,若AD=3,BE=,求CH的长.
27.(10分)如图,在平面直角坐标系中,直线y=﹣2x+6与y轴交于点C、与x轴交于点B,直线AD与y轴交于点A(0,),与直线BC交于点D(1,a).
(1)如图(1)求直线AD的解析式;
(2)如图(2)点P是直线BC上的一点,点P的横坐标是t,求△OCP的面积S与t的函数关系式;
(3)如图(3)在(2)的条件下,将射线CB绕着点C顺时针旋转45°与射线DA交于点Q,当点P在线段DB上,连接PQ,若∠CQP=∠OCB,求点P的坐标.
2023-2024学年黑龙江省哈尔滨市南岗区萧红中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题:(每小题3分,共计36分)
1.(3分)﹣3的倒数是( )
A.3 B. C.﹣ D.﹣3
【解答】解:∵﹣3×(﹣)=1,
∴﹣3的倒数是﹣.
故选:C.
2.(3分)下列四个汽车标志图中,不是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形,故错误;
B、不是轴对称图形,故正确;
C、是轴对称图形,故错误;
D、是轴对称图形,故错误.
故选:B.
3.(3分)下列运算正确的是( )
A.x3 x2=x6 B.x6÷x2=x3 C.x3+x3=2x3 D.(x2)3=x5
【解答】解:A、x3 x2=x5,选项A不正确,不符合题意;
B、x6÷x2=x4,选项B不正确,不符合题意;
C、x3+x3=2x3,选项C正确,符合题意;
D、(x2)3=x6,选项D不正确,不符合题意.
故选:C.
4.(3分)一组数据﹣1,5,5,1,3,4,5的众数、中位数分别为( )
A.5、4 B.5、5 C.5、3 D.5、1
【解答】解:数据从小到大排列为:﹣1,1,3,4,5,5,5,
所以中位数为4,
数据5出现了3次,最多,
所以这组数据的众数为5.
故选:A.
5.(3分)如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A的仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
A.20tan37° B. C. D.20sin37°
【解答】解:如图,在直角△ABC中,∠B=90°,∠C=37°,BC=20m,
∴tanC=,
则AB=BC tanC=20tan37°.
故选:A.
6.(3分)方程=0的解是( )
A.﹣1 B.2 C.5 D.无解
【解答】解:分式方程+=0,
去分母得:x﹣2+3=0,
解得:x=﹣1,
经检验x=﹣1是分式方程的解.
故选:A.
7.(3分)某果园2012年水果产量为100吨,2014年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
A.144(1﹣x)2=100 B.100(1﹣x)2=144
C.144(1+x)2=100 D.100(1+x)2=144
【解答】解:设该果园水果产量的年平均增长率为x,则2013年的产量为100(1+x)吨,2014年的产量为100(1+x)(1+x)=100(1+x)2吨,
根据题意,得100(1+x)2=144,
故选:D.
8.(3分)如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(﹣2,﹣2),(2,﹣2),则顶点D的坐标是( )
A.(﹣4,﹣1) B.(4,﹣2) C.(4,1) D.(2,1)
【解答】解:∵平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(﹣2,﹣2),(2,﹣2),
∴AD=BC=2﹣(﹣2)=4,
∵BC∥x轴,AD∥BC,
∴AD∥x轴,
∴D(4,1),
故选:C.
9.(3分)在平行四边形ABCD中,已知∠A:∠B=1:2,则∠B的度数是( )
A.45° B.90° C.120° D.135°
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A:∠B=1:2,
∴∠B=180°×=120°.
故选:C.
10.(3分)如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,则下列结论中一定正确的是( )
A.= B.= C.= D.=
【解答】解:∵AD∥BE∥CF,
∴,故A错误;
,故C错误;
,故D正确.
故选:D.
11.(3分)受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.若该用户本月用水21吨,则应交水费( )
A.52.5元 B.45元 C.42元 D.37.8元
【解答】解:设直线AB解析式为y=kx+b,把(15,27)(20,39.5)代入得:,
解之得:即y=2.5x﹣10.5,当x=21时,y=42.
故选:C.
12.(3分)如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的 KLMN,若中间空白部分四边形OPQR恰好是正方形,且 KLMN的面积为50,则正方形EFGH的面积为( )
A.24 B.25 C.26 D.27
【解答】解:如图,设PM=PL=NR=KR=a,正方形ORQP的边长为b.
由题意:a2+b2+(a+b)(a﹣b)=50,
∴a2=25,
∴正方形EFGH的面积=a2=25,
故选:B.
二、填空题:(每小题3分,共24分)
13.(3分)我国平均每平方千米的土地一年从太阳得到的能量,相当于燃烧130 000 000kg的煤所产生的能量.把130 000 000kg用科学记数法可表示为 1.3×108 kg.
【解答】解:130 000 000=1.3×108,
故答案为:1.3×108.
14.(3分)在函数y=中,自变量x的取值范围是 x≥﹣3 .
【解答】解:根据题意得:x+3≥0,解得:x≥﹣3.
故答案为:x≥﹣3.
15.(3分)把2a2﹣4a因式分解的结果是 2a(a﹣2) .
【解答】解:原式=2a(a﹣2),
故答案为:2a(a﹣2).
16.(3分)计算:﹣的结果是 .
【解答】解:=2﹣=.
故答案为:.
17.(3分)不等式组的解集是 1<x<2 .
【解答】解:,
∵解不等式①得:x>1,
解不等式②得:x<2,
∴不等式组的解集为1<x<2,
故答案为:1<x<2;
18.(3分)在Rt△ABC中,∠C=90°,BC=12,AC=5,则tanB的值为 .
【解答】解:在Rt△ABC中,∠C=90°,
∴tanB==.
故答案为.
故答案为:.
19.(3分)已知菱形ABCD的边长是6,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则的值是 2或 .
【解答】解:分两种情况:
(1)点E在线段AD上时,△AEM∽△CBM,∴=2;
(2)点E在线段AD的延长线上时,△AME∽△CMB,∴=.
20.(3分)如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为 .
【解答】解:∵四边形ABCD是矩形,点G是DF的中点,
∴AG=DG,
∴∠ADG=∠DAG,
∵AD∥BC,
∴∠ADG=∠CED,
∴∠AGE=∠ADG+∠DAG=2∠CED,
∵∠AED=2∠CED,
∴∠AED=∠AGE,
∴AE=AG=4,
在Rt△ABE中,AB===.
故答案为:.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
【解答】解:原式=
=
=,
x=4sin45°﹣2cos60°
=4×﹣2×
=,
∴当x=时,原式====.
22.(7分)如图,在小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
(1)在图1中画一个以线段AB为一边的平行四边形ABCD,点C、D均在小正方形的顶点上,且平行四边形ABCD的面积为10;
(2)在图2中画一个钝角三角形ABE,点E在小正方形的顶点上,且三角形ABE的面积为4,tan∠AEB=.请直接写出BE的长.
【解答】解:(1)如图1所示;
(2)如图2所示;
BE==2.
23.(8分)“中秋节”是我国的传统佳节,民间历来有吃“月饼”的习俗.某食品厂为了解市民对去年销量较好的五仁月饼(A)、豆沙馅月饼(B)、红枣馅月饼(C)、蛋黄馅月饼(D)四种不同口味月饼的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成两幅不完整的统计图.
请根据以上信息回答:
(1)本次参加抽样调查的居民人数是多少人?
(2)将两幅统计图补充完整;
(3)若该居民区有8000人,请估计爱吃D月饼的是多少人?
【解答】解:(1)本次参加抽样调查的居民的人数是:60÷10%=600(人);
(2)C类的人数是:600﹣180﹣60﹣240=120(人),所占的百分比是:×100%=20%,
A类所占的百分比是:×100%=30%.
A 类所占的百分比是:1﹣10%﹣20%﹣40%=30%.补图
(3))8000×40%=3200(人).
答:估计爱吃D 月饼的人数为3200人.
24.(8分)如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,
(1)如图(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若EG平分∠HEF,在不添加辅助线的条件下,直接写出长度等于EH的线段(不包括EH)
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,且AE=CG,AH=CF
∴△AEH≌△CGF(SAS),
∴EH=GF,
同理EF=GH
∴四边形EFGH是平行四边形
(2)∵四边形EFGH是平行四边形
∴EH∥FG
∴∠HEG=∠EGF
∵EG平分∠HEF
∴∠HEG=∠FEG
∴∠EGF=∠FEG
∴EF=FG,且四边形EFGH是平行四边形
∴四边形EFGH是菱形
∴EH=EF=FG=GH
25.(10分)“六一”儿童节前夕,某时装店老板到厂家选购A、B两种品牌的儿童时装,若购进A品牌的时装5套,B品牌的时装6套,需要950元;若购进A品牌的时装3套,B品牌的时装2套,需要450元.
(1)求A、B两种品牌的时装每套进价分别为多少元?
(2)若1套A品牌的时装售价130元,1套B品牌的时装售价102元,时装店将购进的A、B两种服装共50套全部售出,所获利润要不少于1460元,问A品牌服装至少购进多少套?
【解答】解:(1)设A种品牌的时装每套进价为x元,B种品牌的时装每套进价为y元,依题意有
,
解得.
故A种品牌的时装每套进价为100元,B种品牌的时装每套进价为75元;
(2)设A种品牌的时装购进m套,则B种品牌的时装购进(50﹣m)套,依题意有
(130﹣100)m+(102﹣75)(50﹣m)≥1460,
解得m≥36,
∵m为正整数,
∴A品牌服装至少购进37套.
26.(10分)在综合实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD,点E在射线AB上,现将矩形折叠,折痕为DE,点A的对应点记为点F.
(1)操作发现:如图1,若点F恰好落在矩形ABCD的边BC上,直接写出一个与△BEF相似的三角形;
(2)深入探究:如图2,若点F落在矩形ABCD的边BC的下方时,EF、DF分别交BC于点M、N,过点F作FG⊥BC,FH⊥DC,垂足分别为点G、H,当点G是BC的中点时,试判断△DEF与△DFH是否相似,并证明你的结论;
(3)问题解决:在(2)的条件下,若AD=3,BE=,求CH的长.
【解答】解:(1)△CFD与△BEF相似的三角形,
∵四边形ABCD是矩形,
∴∠B=∠C=∠A=90°,
∴∠BFE+∠BEF=90°,
由折叠的性质可知,∠DFE=∠A=90°,
∴∠BFE+∠CFD=90°,
∴∠BEF=∠CFD,
∴△BEF∽△CFD;
(2)△DEF∽△DFH,
理由:如解图,分别延长HF,AB交于点P,
∵四边形ABCD是矩形,
∴∠ABC=∠ADC=90°,
∵FH⊥CD,
∴∠DHF=90°,
∴四边形 BPFG、四边形GFHC、四边形APHD都是矩形,
∴∠P=∠H=∠A=90°,
∴∠PFE+∠PEF=90°,
由折叠的性质可知,∠DFE=∠A=90°,
∴∠PFE+∠HFD=90°,
∴∠PEF=∠HFD,
∴△PEF∽△HFD,
∴,
∵BG=MP,CG=FH,点G是BG的中点,
∴BG=CG,
∴PF=FH,
∴,
∵∠DFE=∠H=90°,
∴△DEF∽△DFH;
(3)∵由(2)可知,△DEF∽△DFH,
∴∠EDF=∠FDH,
由折叠的性质可知,∠EDF=∠ADE,DF=AD=3,
∴∠ADE=∠EDF=∠FDH=30°,
DH=DF cos30°=,
①当点E在AB上时,如解图,
AE=AD=×3=,
∴AB=AE+BE=+=,
∴CH=DH﹣CD=DH﹣AB=﹣=,
②当点E在AB的延长线上时,如解图,
AE=AD=×3=,
∴AB=AE﹣BE=﹣=,
∴CH=DH﹣CD=DH﹣AB=﹣=,
综上所述,CH的长为:或.
27.(10分)如图,在平面直角坐标系中,直线y=﹣2x+6与y轴交于点C、与x轴交于点B,直线AD与y轴交于点A(0,),与直线BC交于点D(1,a).
(1)如图(1)求直线AD的解析式;
(2)如图(2)点P是直线BC上的一点,点P的横坐标是t,求△OCP的面积S与t的函数关系式;
(3)如图(3)在(2)的条件下,将射线CB绕着点C顺时针旋转45°与射线DA交于点Q,当点P在线段DB上,连接PQ,若∠CQP=∠OCB,求点P的坐标.
【解答】解:(1)把点D(1,a)代入y=﹣2x+6,得:
∴a=﹣2×1+6=4,
∴点D的坐标为(1,4),
设直线AD解析式为y=kx+b,把点D(1,4)、A(0,)代入y=kx+b,
得:,
∴,
∴直线AD解析式为y=x+,
(2)过P点作PH⊥y轴,
y=﹣2x+6 当x=0 时,y=6,
∴C(0,6),
∴OC=6,
当P点在y轴右侧时,
当t>0,
∴△OCP的面积S=OC PH=×6×t=3t,
当P点在y轴左侧时,当t<0时,
∴△OCP的面积S=OC PH=×6×(﹣t)=﹣3t,
即S与t的函数关系式为:S=3t(t>0)或S=﹣3t(t<0);
(3)如图,过点B作BE⊥BC,交直线CQ于E,过E作EF⊥x轴于F,
在△OBC和△FEB中,
,
∴△OBC≌△FEB(ASA),
∴E(﹣3,﹣3),C(0,6),
∴直线CQ解析式可求为:y=3x+6,
,
解得,
∴Q(﹣3,﹣3),
∴点 Q与点E重合,
过点Q作QM⊥y轴,过P作PH⊥x轴,
PH=﹣2t+6,QM=3,
∵∠CQP=∠OCB,
∴△POH为等腰直角三角形,
∴﹣2t+6=t.
∴t=2.
∴P(2,2).
第1页(共1页)
同课章节目录
