黑龙江省哈尔滨市香坊区德强学校2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市香坊区德强学校2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 09:56:47 | ||
图片预览


文档简介
2023-2024学年黑龙江省哈尔滨市香坊区德强学校九年级(上)开学数学试卷(五四学制)
一.选择题(每题3分,共30分)
1.(3分)在直角三角形中,各边的长度都扩大10倍,则锐角A的三角函数值( )
A.也扩大10倍 B.缩小为原来的
C.都不变 D.有的扩大,有的缩小
2.(3分)点(2,﹣3)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,3) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣6,﹣1)
3.(3分)下列图形中是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
4.(3分)已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AC等于( )
A.6 B. C.10 D.12
5.(3分)如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
A.3 B.4 C.6 D.8
6.(3分)如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A.5cosa B. C.5sina D.
7.(3分)如图,AB是⊙O的直径,∠B=30°,BC=3,则AC的长为( )
A. B. C.1 D.
8.(3分)如图,把△ABC绕点C顺时针旋转某个角度a得到△A'B'C,∠A=30°,∠1=50°,则旋转角a等于( )
A.110° B.70° C.40° D.20°
9.(3分)下列说法中,正确的个数有( )
①长度相等的弧是等弧;
②平分弦的直径垂直于弦,并且平分弦所对的两条弧;
③如果两个圆心角相等,那么它们所对的弦相等;
④反比例函数的图象经过一三象限;
⑤中心对称的两个图形是全等的.
A.1 B.2 C.3 D.4
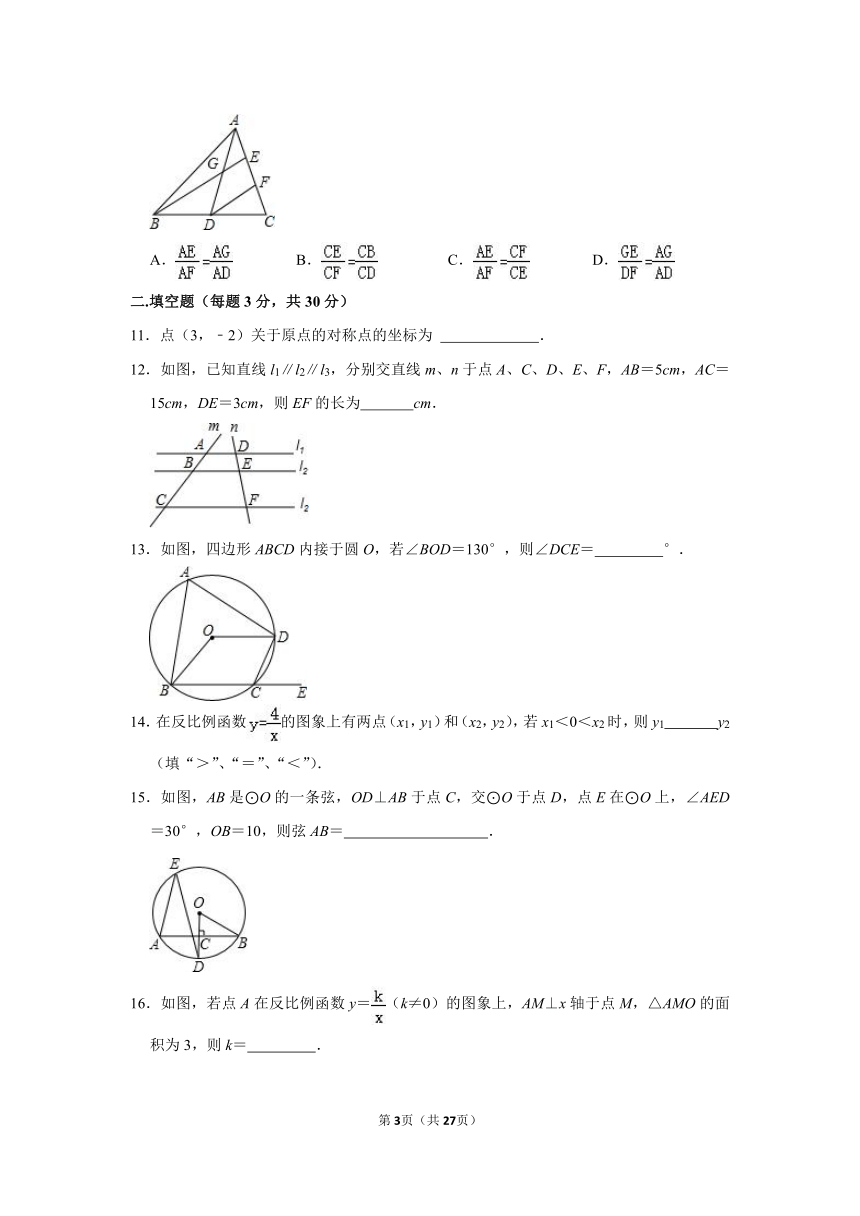
10.(3分)如图,△ABC中,DF∥BE,AD、BE相交于点G,下列结论错误的是( )
A. B. C. D.
二.填空题(每题3分,共30分)
11.点(3,﹣2)关于原点的对称点的坐标为 .
12.如图,已知直线l1∥l2∥l3,分别交直线m、n于点A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为 cm.
13.如图,四边形ABCD内接于圆O,若∠BOD=130°,则∠DCE= °.
14.在反比例函数的图象上有两点(x1,y1)和(x2,y2),若x1<0<x2时,则y1 y2(填“>”、“=”、“<”).
15.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= .
16.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k= .
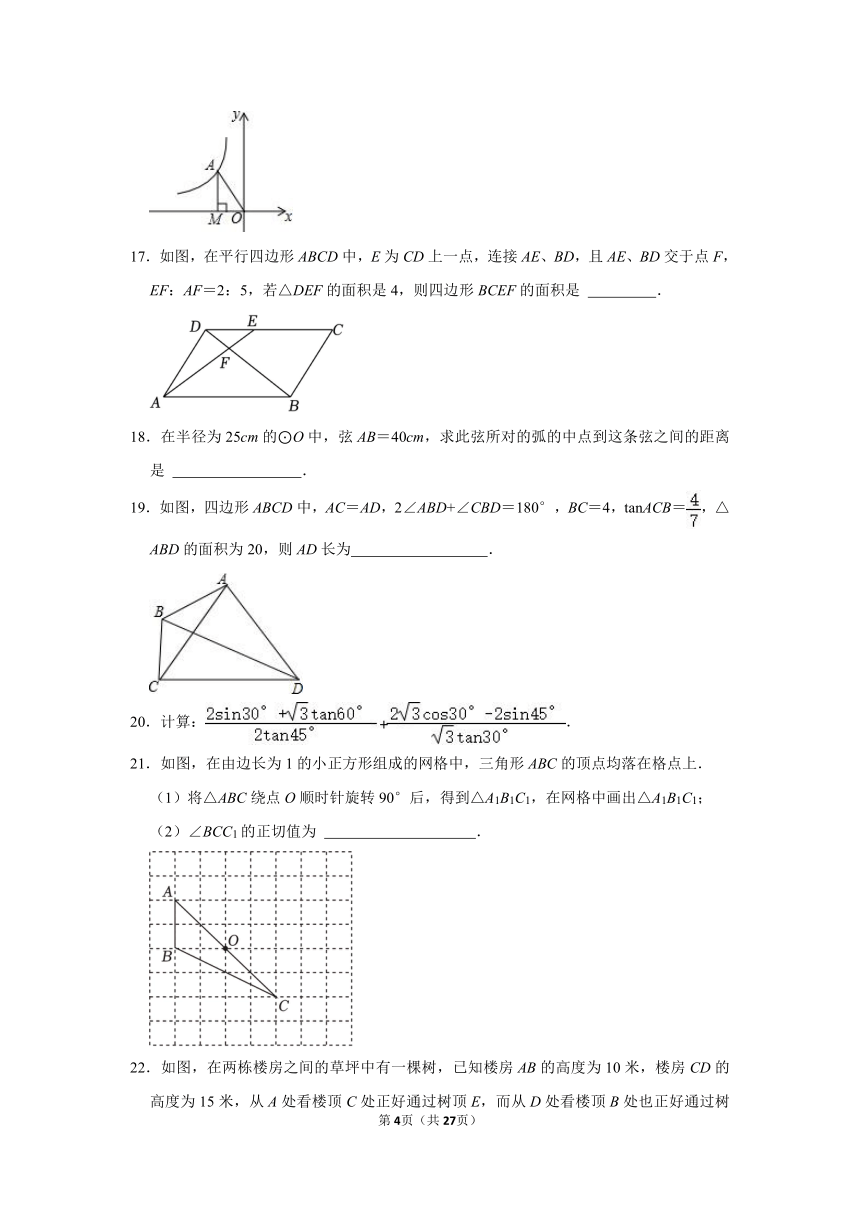
17.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,EF:AF=2:5,若△DEF的面积是4,则四边形BCEF的面积是 .
18.在半径为25cm的⊙O中,弦AB=40cm,求此弦所对的弧的中点到这条弦之间的距离是 .
19.如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=,△ABD的面积为20,则AD长为 .
20.计算:.
21.如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1,在网格中画出△A1B1C1;
(2)∠BCC1的正切值为 .
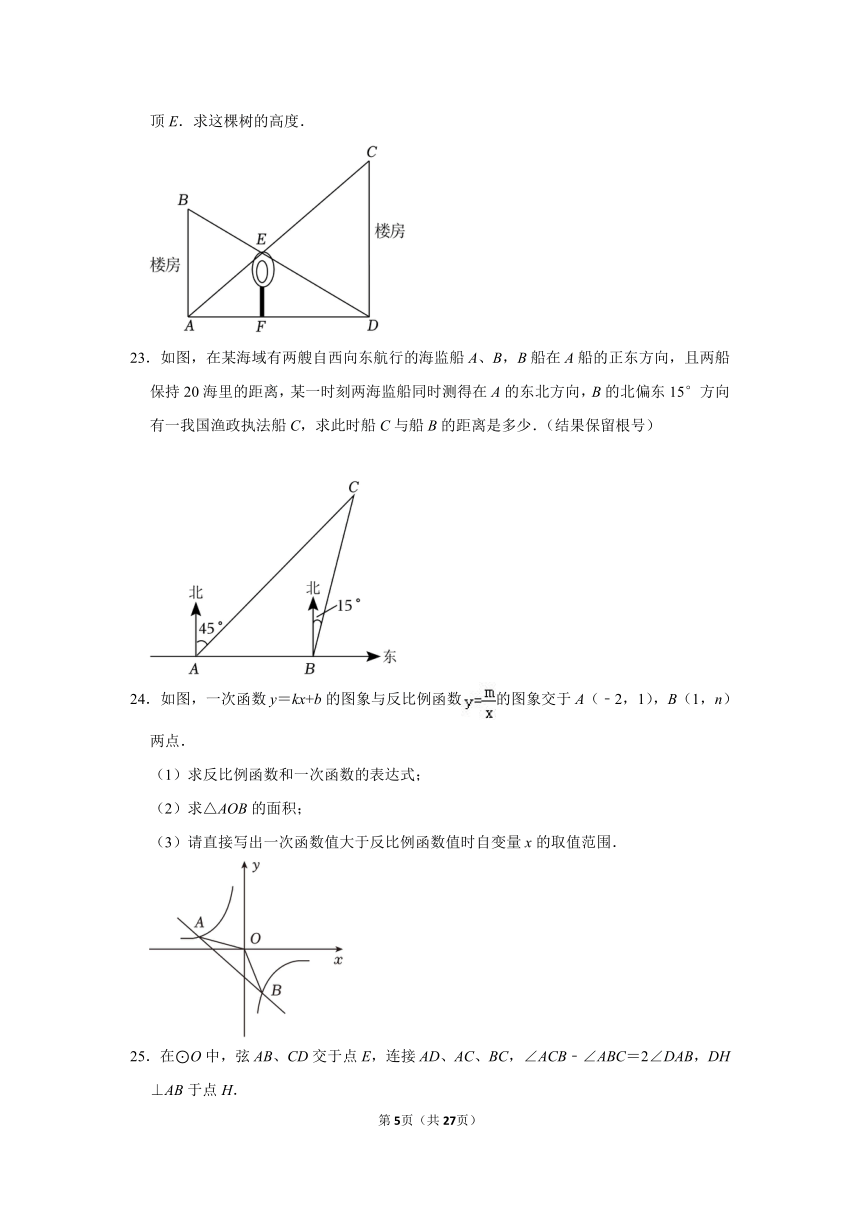
22.如图,在两栋楼房之间的草坪中有一棵树,已知楼房AB的高度为10米,楼房CD的高度为15米,从A处看楼顶C处正好通过树顶E,而从D处看楼顶B处也正好通过树顶E.求这棵树的高度.
23.如图,在某海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
24.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)请直接写出一次函数值大于反比例函数值时自变量x的取值范围.
25.在⊙O中,弦AB、CD交于点E,连接AD、AC、BC,∠ACB﹣∠ABC=2∠DAB,DH⊥AB于点H.
(1)求证:∠BAC=2∠EDH;
(2)M为弦BC中点,过点M作MF⊥DC,连接HF,并延长HF交AC于G,3AG=2BH,求证:FH=FG;
(3)在(2)的条件下,若BC=2CE,EF=2,求⊙O的直径.
26.在平面直角坐标系中,O为坐标原点,直线AB交x轴的正半轴于点A(6,0),交y轴的负半轴于点B,且tan∠.
(1)如图1,求直线AB的解析式;
(2)如图2,P为线段AB上一点,点C的坐标为,连接CP,设点P的横坐标为t,△BCP的面积为S,求S与t的函数关系式;(不需要写出自变量t的取值范围);
(3)如图3,在(2)的条件下,点D的坐标为,点E、F都在y轴的负半轴上,且点E在点F的上方,连接DE、AC、AE、AF,且∠EDO=∠ACO,若AE平分∠BAF,AF=2AP,连接FP交AE于点G,求点G的坐标.
2023-2024学年黑龙江省哈尔滨市香坊区德强学校九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一.选择题(每题3分,共30分)
1.(3分)在直角三角形中,各边的长度都扩大10倍,则锐角A的三角函数值( )
A.也扩大10倍 B.缩小为原来的
C.都不变 D.有的扩大,有的缩小
【解答】解:设原来直角三角形的两条直角边为a,b,斜边为c,则扩大后的直角三角形的两条直角边为10a,10b,斜边为10c,
原来的直角三角形的sinA=,cosA=,tanA=,
扩大后的直角三角形的sinA==,cosA==,tanA==,
由上可得,在直角三角形中,各边的长度都扩大10倍,则锐角A的三角函数值都不变,
故选:C.
2.(3分)点(2,﹣3)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,3) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣6,﹣1)
【解答】解:∵点(2,﹣3)在反比例函数y=的图象上,
∴k=2×(﹣3)=6.
A、∵2×3=6≠﹣6,∴此点不在函数图象上;
B、∵3×(﹣2)=﹣6,∴此点,在函数图象上;
C、∵(﹣2)×(﹣3)=6≠﹣6,此点不在函数图象上;
D、∵(﹣1)×(﹣6)=6≠﹣6,此点不在函数图象上.
故选:B.
3.(3分)下列图形中是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
【解答】解:A选项中的图形既不是中心对称图形,也不是轴对称图形,不符合题意;
B选项中的图形既是中心对称图形,又是轴对称图形,不符合题意;
C选项选项中的图形是中心对称图形但不是轴对称图形,符合题意;
D选项中的图形是轴对称图形,但不是中心对称图形,不符合题意;
故选:C.
4.(3分)已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AC等于( )
A.6 B. C.10 D.12
【解答】解:∵Rt△ABC中,∠C=90°,tanA=,BC=8,
∴tanA=,AC==6.
故选:A.
5.(3分)如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
A.3 B.4 C.6 D.8
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴AD:AB=AE:AC,
而AD:AB=3:4,AE=6,
∴3:4=6:AC,
∴AC=8.
故选:D.
6.(3分)如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A.5cosa B. C.5sina D.
【解答】解:由于相邻两树之间的水平距离为5米,坡角为α,
则两树在坡面上的距离AB=.
故选:B.
7.(3分)如图,AB是⊙O的直径,∠B=30°,BC=3,则AC的长为( )
A. B. C.1 D.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=30°,
∵tanB==tan30°=,BC=3,
∴AC=.
故选:A.
8.(3分)如图,把△ABC绕点C顺时针旋转某个角度a得到△A'B'C,∠A=30°,∠1=50°,则旋转角a等于( )
A.110° B.70° C.40° D.20°
【解答】解:∵△ABC绕点C顺时针旋转某个角度α得到△A′B′C,
∴∠A=∠A′=30°,
又∵∠1=∠A′+∠ACA′=50°,
∴∠BCB′=∠ACA′=20°,
故选:D.
9.(3分)下列说法中,正确的个数有( )
①长度相等的弧是等弧;
②平分弦的直径垂直于弦,并且平分弦所对的两条弧;
③如果两个圆心角相等,那么它们所对的弦相等;
④反比例函数的图象经过一三象限;
⑤中心对称的两个图形是全等的.
A.1 B.2 C.3 D.4
【解答】解:在同圆或等圆中,长度相等的弧是等弧,故①错误,不符合题意;
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,故②错误,不符合题意;
在同圆或等圆中,如果两个圆心角相等,那么它们所对的弦相等,故③错误,不符合题意;
反比例函数的图象经过二、四象限,故④错误,不符合题意;
中心对称的两个图形是全等的,故⑤正确,符合题意;
故选:A.
10.(3分)如图,△ABC中,DF∥BE,AD、BE相交于点G,下列结论错误的是( )
A. B. C. D.
【解答】解:∵DF∥BE,
∴△AGE∽△ADF,△CDF∽△CBE,
∴=,=,=,
无法得到=,
故结论正确的是A、B、D,结论错误的是C.
故选:C.
二.填空题(每题3分,共30分)
11.点(3,﹣2)关于原点的对称点的坐标为 (﹣3,2) .
【解答】解:点(3,﹣2)关于原点的对称点的坐标为(﹣3,2),
故答案为:(﹣3,2).
12.如图,已知直线l1∥l2∥l3,分别交直线m、n于点A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为 6 cm.
【解答】解:∵直线l1∥l2∥l3,
∴,即,
∴EF=6,
故答案为:6.
13.如图,四边形ABCD内接于圆O,若∠BOD=130°,则∠DCE= 65 °.
【解答】解:∵∠BOD=130°,
∴∠A=∠BOD=65°,
∵∠A+∠BCD=180°,∠DCE+∠BCD=180°,
∴∠DCE=∠A=65°.
故答案为:65.
14.在反比例函数的图象上有两点(x1,y1)和(x2,y2),若x1<0<x2时,则y1 < y2(填“>”、“=”、“<”).
【解答】解:反比例函数,
∴该函数的图象位于第一、三象限,在每个象限内,y随x的增大而减小,第一象限内的y都大于0,第三象限内的y都小于0,
∵x1<0<x2,
∴y1<y2,
故答案为:<.
15.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= 10 .
【解答】解:∵OD⊥AB,
∴AC=BC,=,
∵∠AED=30°,
∴∠BOD=2∠AED=60°,
在RT△OBC中,sin∠COB=,
∴OB=10,
∴=,
∴AB=2BC=10.
故答案为10.
16.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k= ﹣6 .
【解答】解:因为△AOM的面积是3,
所以|k|=2×3=6.
又因为图象在二,四象限,k<0,
所以k=﹣6.
故答案为:﹣6.
17.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,EF:AF=2:5,若△DEF的面积是4,则四边形BCEF的面积是 31 .
【解答】解:∵四边形ABCD为平行四边形,
∴CD∥AB.
∴△DEF∽△BAF.
∴==.
∴==,==.
设S△DEF=S,则S△ABF=S,S△ADF=S.
∴S△ABD=S△ADF+S△ABF=S+=S=S.
∵四边形ABCD为平行四边形,
∴S△ABD=S△DBC=S.
∴S四边形EFBC=S△BDC﹣S△DEF=S﹣S=S.
又S=4,
∴S四边形EFBC=×4=31.
故答案为:31.
18.在半径为25cm的⊙O中,弦AB=40cm,求此弦所对的弧的中点到这条弦之间的距离是 10cm或40cm. .
【解答】解:点C和D为弦AB所对弧的中点,连接CD交AB于E,连接OA,如图,
∵点C和D为弦AB所对弧的中点,
∴CD为直径,CD⊥AB,
∴AE=BE=AB=20,
在Rt△OAE中,∵OA=25cm,AE=20cm,
∴OE==15(cm),
∴DE=OD+OE=40(cm),CE=OC﹣OE=10(cm),
即弦AB和弦AB所对的劣弧的中点的距离为10cm,弦AB和弦AB所对的优弧的中点的距离为40cm.
故答案为:10cm或40cm.
19.如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=,△ABD的面积为20,则AD长为 .
【解答】解:如图作AE⊥CB于E,AF⊥BD于F.
∵2∠ABD+∠CBD=180°,∠CBD+∠ABD+∠ABE=180°,
∴∠ABE=∠ABF,
∴AE=AF,
在Rt△ACE和Rt△ADF中,
,
∴△ACE≌△ADF,
∴CE=DF,∠ACE=∠ADF,设AE=AF=4x,
∵∠tan∠ACE=tan∠ADF=,
∴==,
∴CE=DF=7x,BE=BF=7x﹣4,
∵S△ABD=20,
∴(7x+7x﹣4) 4x=20,
∴x=1或﹣(舍弃),
∴AD===,
故答案为.
20.计算:.
【解答】解:原式=+
=+
=2+3﹣
=5﹣.
21.如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1,在网格中画出△A1B1C1;
(2)∠BCC1的正切值为 .
【解答】解:(1)如图:△A1B1C1即为所求;
(2)∠BCC1的正切值为:=,
故答案为:.
22.如图,在两栋楼房之间的草坪中有一棵树,已知楼房AB的高度为10米,楼房CD的高度为15米,从A处看楼顶C处正好通过树顶E,而从D处看楼顶B处也正好通过树顶E.求这棵树的高度.
【解答】解:∵AB∥CD,
∴△ABE∽△CDE,
∴,
∵EF∥AB,
∴△FDE∽△ADB,
∴,
∵AB=10,
∴EF=6.
答:这棵树的高度为6米.
23.如图,在某海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
【解答】解:过点B作BD⊥AC于D.
由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=30°,
在Rt△ABD中,BD=AB sin∠BAD=20×=10(海里),
在Rt△BCD中,BC=(海里).
答:此时船C与船B的距离是20海里.
24.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)请直接写出一次函数值大于反比例函数值时自变量x的取值范围.
【解答】解:(1)∵A(﹣2,1)在反比例函数的图象上,
∴m=﹣2,
∴反比例函数解析式为:y=﹣;
∵点B(1,n)在y=﹣图象上,
∴n=﹣2,
∴B(1,﹣2),
∵A(﹣2,1),B(1,﹣2)在一次函数y=kx+b的图象上,
∴,解得:
,
∴一次函数解析式为:y=﹣x﹣1.
(2)设直线y=﹣x﹣1与y轴的交点为C,则C(0,﹣1),即OC=1,
S△AOB=S△AOC+S△BOC=×1×2+×1×1=;
(3)根据图像,一次函数值大于反比例函数值时自变量x的取值范围为:x<﹣2或0<x<1.
25.在⊙O中,弦AB、CD交于点E,连接AD、AC、BC,∠ACB﹣∠ABC=2∠DAB,DH⊥AB于点H.
(1)求证:∠BAC=2∠EDH;
(2)M为弦BC中点,过点M作MF⊥DC,连接HF,并延长HF交AC于G,3AG=2BH,求证:FH=FG;
(3)在(2)的条件下,若BC=2CE,EF=2,求⊙O的直径.
【解答】(1)证明:∵∠ACB﹣∠ABC=2∠DAB,∠DAB=∠DCB,
∴∠ACB﹣∠ABC=2∠DCB,
∴∠ACB﹣∠DCB=∠ABC+∠DCB=∠AEC,
∴∠ACE=∠AEC,
∵∠EAC+∠ACE+∠AEC=180°,
∴∠EAC+2∠AEC=180°,
∵DH⊥AB,
∴∠DHE=90°,
∴∠DEH+∠EDH=90°,
∴2∠DEH+2∠EDH=180°,
∵∠AEC=∠DEH,
∴2∠AEC+2∠EDH=180°,
∴∠EAC=2∠EDH,即∠BAC=2∠EDH;
(2)证明:如图2,过点B作BK⊥DC于点K,连接KM、HK、BD,
∵BK⊥CD,
∴∠BKC=90°,
∵M为BC的中点,
∴MK=BC=BM=MC,
∵∠DBA=∠DCA,∠DEB=∠AEC=∠ACE,
∴∠DEB=∠DBE,
∴BD=DE,
∵DH⊥AB,
∴BH=EH,
在Rt△BEK中,HK=BE=HB=EH,
∴∠HKE=∠HEK,
∴∠HKF=∠GCF,
∵MF⊥DC,MK=MC,
∴FK=CF,
在△HFK和△GFC中,
,
∴△HFK≌△GFC(ASA),
∴FH=FG;
(3)解:如图3,过点G作GP∥AB交DC于点P,连接EM,
∵GP∥AB,
∴∠EHF=∠PGF,
∵FH=FG,∠EFH=∠PFG,
∴△FHE≌△FGP(ASA),
∴EF=PF=EP,
∵△HFK≌△GFC,
∴HK=CG,
∵HK=HB=HE,
∴CG=HB=HE,
∵3AG=2BH,
∴=,
∵GP∥AE,
∴==,
∵EF=PF,
∴EF=EC,
∵EF=2,
∴EC=10,
∵BC=2CE,MB=MC,
∴MC=MB=CE=10,
∴∠CEM=∠CME,
过点E作EQ⊥BC于点Q,
∵EQ⊥BC,
∴∠EQC=∠EQB=∠MFE=90°,
∵EM=ME,
∴△EFM≌△MQE(AAS),
∴MQ=EF=2,
∴CF=CQ=10﹣2=8,
在Rt△MFC中,由勾股定理得:FM2+FC2=MC2,
即FM2+82=102,
解得:FM=6(负值已舍去),
∴EQ=6,
∴tan∠ECQ===,
∵BQ=BM+MQ=10+2=12,
∴tan∠EBQ===,
∴BE===6,
取EC的中点T,连接AT,过点C作CR⊥AB于点R,
∵∠AEC=∠ACE,
∴AE=AC,
∵TE=TC,
∴AT⊥DC,∠EAT=∠CAT,
∵tan∠CBR=,BC=20,
∴BR=2CR,
由勾股定理得:CR==,
解得:CR=4,
∴BR=8,
∴ER=BR﹣BE=8﹣6=2,
∴tan∠REC===2,
∴tan∠EAT=tan∠CAT=,
∵tan∠ADC=tan∠ABC==,
∴tan∠CAT=tan∠ADC=,
设AT=2k,
∴DT=2AT=4k,TC=k,
∴DC=5k,
∵tan∠CAT=tan∠ADC,
∴∠CAT=∠ADC,
∵∠CAT+∠ACD=90°,
∴∠ADC+∠ACD=90°,
∴∠DAC=90°,
∴DC为直径,
∵EC=10,
∴ET=CT=5,
∵DC=5TC,
∴DC=25,
∴⊙O的直径为25.
26.在平面直角坐标系中,O为坐标原点,直线AB交x轴的正半轴于点A(6,0),交y轴的负半轴于点B,且tan∠.
(1)如图1,求直线AB的解析式;
(2)如图2,P为线段AB上一点,点C的坐标为,连接CP,设点P的横坐标为t,△BCP的面积为S,求S与t的函数关系式;(不需要写出自变量t的取值范围);
(3)如图3,在(2)的条件下,点D的坐标为,点E、F都在y轴的负半轴上,且点E在点F的上方,连接DE、AC、AE、AF,且∠EDO=∠ACO,若AE平分∠BAF,AF=2AP,连接FP交AE于点G,求点G的坐标.
【解答】解:(1)∵∠AOB=90°,
∴tan∠OAB=,
∵A(6,0),
∴OA=6,
∴OB=,
∴B(0,﹣),
设直线AB的解析式为:y=kx+b,
∴,
∴,
∴y=﹣;
(2)∵C,B(0,﹣),
∴BC=,
∴S△BCP=BC xP=,
∴S=;
(3)如图,
作PQ⊥OA于Q,
∵∠AOC=∠DOE,∠EDO=∠ACO,
∴△AOC∽△EOD,
∴,
∴,
∴OE=2,
∴BE=OE﹣OB=,
∵AE平分∠BAF,
∴,
∴,
∴,
设EF=m,则AF=m,
在Rt△AOF中,OA=6,OF=OE+EF=m+2,AF=m,
∴62+(m+2)2=(m)2,
m1=,m2=﹣(舍去),
∴AF=,
∴AP=AF=,
∵PQ∥OB,
∴△APQ∽△ABO,
∴,
∴=,
∴AQ=4,PQ=,
∴OQ=2,
∴P(2,﹣),
∵F(0,﹣),
∴直线PF的解析式为:y=x﹣,
∵A(6,0),E(0,﹣2),
∴y=x﹣2,
由得,
x=,
当x=时,y==﹣,
∴G(,﹣).
第1页(共1页)
一.选择题(每题3分,共30分)
1.(3分)在直角三角形中,各边的长度都扩大10倍,则锐角A的三角函数值( )
A.也扩大10倍 B.缩小为原来的
C.都不变 D.有的扩大,有的缩小
2.(3分)点(2,﹣3)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,3) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣6,﹣1)
3.(3分)下列图形中是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
4.(3分)已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AC等于( )
A.6 B. C.10 D.12
5.(3分)如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
A.3 B.4 C.6 D.8
6.(3分)如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A.5cosa B. C.5sina D.
7.(3分)如图,AB是⊙O的直径,∠B=30°,BC=3,则AC的长为( )
A. B. C.1 D.
8.(3分)如图,把△ABC绕点C顺时针旋转某个角度a得到△A'B'C,∠A=30°,∠1=50°,则旋转角a等于( )
A.110° B.70° C.40° D.20°
9.(3分)下列说法中,正确的个数有( )
①长度相等的弧是等弧;
②平分弦的直径垂直于弦,并且平分弦所对的两条弧;
③如果两个圆心角相等,那么它们所对的弦相等;
④反比例函数的图象经过一三象限;
⑤中心对称的两个图形是全等的.
A.1 B.2 C.3 D.4
10.(3分)如图,△ABC中,DF∥BE,AD、BE相交于点G,下列结论错误的是( )
A. B. C. D.
二.填空题(每题3分,共30分)
11.点(3,﹣2)关于原点的对称点的坐标为 .
12.如图,已知直线l1∥l2∥l3,分别交直线m、n于点A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为 cm.
13.如图,四边形ABCD内接于圆O,若∠BOD=130°,则∠DCE= °.
14.在反比例函数的图象上有两点(x1,y1)和(x2,y2),若x1<0<x2时,则y1 y2(填“>”、“=”、“<”).
15.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= .
16.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k= .
17.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,EF:AF=2:5,若△DEF的面积是4,则四边形BCEF的面积是 .
18.在半径为25cm的⊙O中,弦AB=40cm,求此弦所对的弧的中点到这条弦之间的距离是 .
19.如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=,△ABD的面积为20,则AD长为 .
20.计算:.
21.如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1,在网格中画出△A1B1C1;
(2)∠BCC1的正切值为 .
22.如图,在两栋楼房之间的草坪中有一棵树,已知楼房AB的高度为10米,楼房CD的高度为15米,从A处看楼顶C处正好通过树顶E,而从D处看楼顶B处也正好通过树顶E.求这棵树的高度.
23.如图,在某海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
24.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)请直接写出一次函数值大于反比例函数值时自变量x的取值范围.
25.在⊙O中,弦AB、CD交于点E,连接AD、AC、BC,∠ACB﹣∠ABC=2∠DAB,DH⊥AB于点H.
(1)求证:∠BAC=2∠EDH;
(2)M为弦BC中点,过点M作MF⊥DC,连接HF,并延长HF交AC于G,3AG=2BH,求证:FH=FG;
(3)在(2)的条件下,若BC=2CE,EF=2,求⊙O的直径.
26.在平面直角坐标系中,O为坐标原点,直线AB交x轴的正半轴于点A(6,0),交y轴的负半轴于点B,且tan∠.
(1)如图1,求直线AB的解析式;
(2)如图2,P为线段AB上一点,点C的坐标为,连接CP,设点P的横坐标为t,△BCP的面积为S,求S与t的函数关系式;(不需要写出自变量t的取值范围);
(3)如图3,在(2)的条件下,点D的坐标为,点E、F都在y轴的负半轴上,且点E在点F的上方,连接DE、AC、AE、AF,且∠EDO=∠ACO,若AE平分∠BAF,AF=2AP,连接FP交AE于点G,求点G的坐标.
2023-2024学年黑龙江省哈尔滨市香坊区德强学校九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一.选择题(每题3分,共30分)
1.(3分)在直角三角形中,各边的长度都扩大10倍,则锐角A的三角函数值( )
A.也扩大10倍 B.缩小为原来的
C.都不变 D.有的扩大,有的缩小
【解答】解:设原来直角三角形的两条直角边为a,b,斜边为c,则扩大后的直角三角形的两条直角边为10a,10b,斜边为10c,
原来的直角三角形的sinA=,cosA=,tanA=,
扩大后的直角三角形的sinA==,cosA==,tanA==,
由上可得,在直角三角形中,各边的长度都扩大10倍,则锐角A的三角函数值都不变,
故选:C.
2.(3分)点(2,﹣3)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(2,3) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣6,﹣1)
【解答】解:∵点(2,﹣3)在反比例函数y=的图象上,
∴k=2×(﹣3)=6.
A、∵2×3=6≠﹣6,∴此点不在函数图象上;
B、∵3×(﹣2)=﹣6,∴此点,在函数图象上;
C、∵(﹣2)×(﹣3)=6≠﹣6,此点不在函数图象上;
D、∵(﹣1)×(﹣6)=6≠﹣6,此点不在函数图象上.
故选:B.
3.(3分)下列图形中是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
【解答】解:A选项中的图形既不是中心对称图形,也不是轴对称图形,不符合题意;
B选项中的图形既是中心对称图形,又是轴对称图形,不符合题意;
C选项选项中的图形是中心对称图形但不是轴对称图形,符合题意;
D选项中的图形是轴对称图形,但不是中心对称图形,不符合题意;
故选:C.
4.(3分)已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AC等于( )
A.6 B. C.10 D.12
【解答】解:∵Rt△ABC中,∠C=90°,tanA=,BC=8,
∴tanA=,AC==6.
故选:A.
5.(3分)如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
A.3 B.4 C.6 D.8
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴AD:AB=AE:AC,
而AD:AB=3:4,AE=6,
∴3:4=6:AC,
∴AC=8.
故选:D.
6.(3分)如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A.5cosa B. C.5sina D.
【解答】解:由于相邻两树之间的水平距离为5米,坡角为α,
则两树在坡面上的距离AB=.
故选:B.
7.(3分)如图,AB是⊙O的直径,∠B=30°,BC=3,则AC的长为( )
A. B. C.1 D.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=30°,
∵tanB==tan30°=,BC=3,
∴AC=.
故选:A.
8.(3分)如图,把△ABC绕点C顺时针旋转某个角度a得到△A'B'C,∠A=30°,∠1=50°,则旋转角a等于( )
A.110° B.70° C.40° D.20°
【解答】解:∵△ABC绕点C顺时针旋转某个角度α得到△A′B′C,
∴∠A=∠A′=30°,
又∵∠1=∠A′+∠ACA′=50°,
∴∠BCB′=∠ACA′=20°,
故选:D.
9.(3分)下列说法中,正确的个数有( )
①长度相等的弧是等弧;
②平分弦的直径垂直于弦,并且平分弦所对的两条弧;
③如果两个圆心角相等,那么它们所对的弦相等;
④反比例函数的图象经过一三象限;
⑤中心对称的两个图形是全等的.
A.1 B.2 C.3 D.4
【解答】解:在同圆或等圆中,长度相等的弧是等弧,故①错误,不符合题意;
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,故②错误,不符合题意;
在同圆或等圆中,如果两个圆心角相等,那么它们所对的弦相等,故③错误,不符合题意;
反比例函数的图象经过二、四象限,故④错误,不符合题意;
中心对称的两个图形是全等的,故⑤正确,符合题意;
故选:A.
10.(3分)如图,△ABC中,DF∥BE,AD、BE相交于点G,下列结论错误的是( )
A. B. C. D.
【解答】解:∵DF∥BE,
∴△AGE∽△ADF,△CDF∽△CBE,
∴=,=,=,
无法得到=,
故结论正确的是A、B、D,结论错误的是C.
故选:C.
二.填空题(每题3分,共30分)
11.点(3,﹣2)关于原点的对称点的坐标为 (﹣3,2) .
【解答】解:点(3,﹣2)关于原点的对称点的坐标为(﹣3,2),
故答案为:(﹣3,2).
12.如图,已知直线l1∥l2∥l3,分别交直线m、n于点A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为 6 cm.
【解答】解:∵直线l1∥l2∥l3,
∴,即,
∴EF=6,
故答案为:6.
13.如图,四边形ABCD内接于圆O,若∠BOD=130°,则∠DCE= 65 °.
【解答】解:∵∠BOD=130°,
∴∠A=∠BOD=65°,
∵∠A+∠BCD=180°,∠DCE+∠BCD=180°,
∴∠DCE=∠A=65°.
故答案为:65.
14.在反比例函数的图象上有两点(x1,y1)和(x2,y2),若x1<0<x2时,则y1 < y2(填“>”、“=”、“<”).
【解答】解:反比例函数,
∴该函数的图象位于第一、三象限,在每个象限内,y随x的增大而减小,第一象限内的y都大于0,第三象限内的y都小于0,
∵x1<0<x2,
∴y1<y2,
故答案为:<.
15.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= 10 .
【解答】解:∵OD⊥AB,
∴AC=BC,=,
∵∠AED=30°,
∴∠BOD=2∠AED=60°,
在RT△OBC中,sin∠COB=,
∴OB=10,
∴=,
∴AB=2BC=10.
故答案为10.
16.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k= ﹣6 .
【解答】解:因为△AOM的面积是3,
所以|k|=2×3=6.
又因为图象在二,四象限,k<0,
所以k=﹣6.
故答案为:﹣6.
17.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,EF:AF=2:5,若△DEF的面积是4,则四边形BCEF的面积是 31 .
【解答】解:∵四边形ABCD为平行四边形,
∴CD∥AB.
∴△DEF∽△BAF.
∴==.
∴==,==.
设S△DEF=S,则S△ABF=S,S△ADF=S.
∴S△ABD=S△ADF+S△ABF=S+=S=S.
∵四边形ABCD为平行四边形,
∴S△ABD=S△DBC=S.
∴S四边形EFBC=S△BDC﹣S△DEF=S﹣S=S.
又S=4,
∴S四边形EFBC=×4=31.
故答案为:31.
18.在半径为25cm的⊙O中,弦AB=40cm,求此弦所对的弧的中点到这条弦之间的距离是 10cm或40cm. .
【解答】解:点C和D为弦AB所对弧的中点,连接CD交AB于E,连接OA,如图,
∵点C和D为弦AB所对弧的中点,
∴CD为直径,CD⊥AB,
∴AE=BE=AB=20,
在Rt△OAE中,∵OA=25cm,AE=20cm,
∴OE==15(cm),
∴DE=OD+OE=40(cm),CE=OC﹣OE=10(cm),
即弦AB和弦AB所对的劣弧的中点的距离为10cm,弦AB和弦AB所对的优弧的中点的距离为40cm.
故答案为:10cm或40cm.
19.如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=,△ABD的面积为20,则AD长为 .
【解答】解:如图作AE⊥CB于E,AF⊥BD于F.
∵2∠ABD+∠CBD=180°,∠CBD+∠ABD+∠ABE=180°,
∴∠ABE=∠ABF,
∴AE=AF,
在Rt△ACE和Rt△ADF中,
,
∴△ACE≌△ADF,
∴CE=DF,∠ACE=∠ADF,设AE=AF=4x,
∵∠tan∠ACE=tan∠ADF=,
∴==,
∴CE=DF=7x,BE=BF=7x﹣4,
∵S△ABD=20,
∴(7x+7x﹣4) 4x=20,
∴x=1或﹣(舍弃),
∴AD===,
故答案为.
20.计算:.
【解答】解:原式=+
=+
=2+3﹣
=5﹣.
21.如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1,在网格中画出△A1B1C1;
(2)∠BCC1的正切值为 .
【解答】解:(1)如图:△A1B1C1即为所求;
(2)∠BCC1的正切值为:=,
故答案为:.
22.如图,在两栋楼房之间的草坪中有一棵树,已知楼房AB的高度为10米,楼房CD的高度为15米,从A处看楼顶C处正好通过树顶E,而从D处看楼顶B处也正好通过树顶E.求这棵树的高度.
【解答】解:∵AB∥CD,
∴△ABE∽△CDE,
∴,
∵EF∥AB,
∴△FDE∽△ADB,
∴,
∵AB=10,
∴EF=6.
答:这棵树的高度为6米.
23.如图,在某海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
【解答】解:过点B作BD⊥AC于D.
由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=30°,
在Rt△ABD中,BD=AB sin∠BAD=20×=10(海里),
在Rt△BCD中,BC=(海里).
答:此时船C与船B的距离是20海里.
24.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)请直接写出一次函数值大于反比例函数值时自变量x的取值范围.
【解答】解:(1)∵A(﹣2,1)在反比例函数的图象上,
∴m=﹣2,
∴反比例函数解析式为:y=﹣;
∵点B(1,n)在y=﹣图象上,
∴n=﹣2,
∴B(1,﹣2),
∵A(﹣2,1),B(1,﹣2)在一次函数y=kx+b的图象上,
∴,解得:
,
∴一次函数解析式为:y=﹣x﹣1.
(2)设直线y=﹣x﹣1与y轴的交点为C,则C(0,﹣1),即OC=1,
S△AOB=S△AOC+S△BOC=×1×2+×1×1=;
(3)根据图像,一次函数值大于反比例函数值时自变量x的取值范围为:x<﹣2或0<x<1.
25.在⊙O中,弦AB、CD交于点E,连接AD、AC、BC,∠ACB﹣∠ABC=2∠DAB,DH⊥AB于点H.
(1)求证:∠BAC=2∠EDH;
(2)M为弦BC中点,过点M作MF⊥DC,连接HF,并延长HF交AC于G,3AG=2BH,求证:FH=FG;
(3)在(2)的条件下,若BC=2CE,EF=2,求⊙O的直径.
【解答】(1)证明:∵∠ACB﹣∠ABC=2∠DAB,∠DAB=∠DCB,
∴∠ACB﹣∠ABC=2∠DCB,
∴∠ACB﹣∠DCB=∠ABC+∠DCB=∠AEC,
∴∠ACE=∠AEC,
∵∠EAC+∠ACE+∠AEC=180°,
∴∠EAC+2∠AEC=180°,
∵DH⊥AB,
∴∠DHE=90°,
∴∠DEH+∠EDH=90°,
∴2∠DEH+2∠EDH=180°,
∵∠AEC=∠DEH,
∴2∠AEC+2∠EDH=180°,
∴∠EAC=2∠EDH,即∠BAC=2∠EDH;
(2)证明:如图2,过点B作BK⊥DC于点K,连接KM、HK、BD,
∵BK⊥CD,
∴∠BKC=90°,
∵M为BC的中点,
∴MK=BC=BM=MC,
∵∠DBA=∠DCA,∠DEB=∠AEC=∠ACE,
∴∠DEB=∠DBE,
∴BD=DE,
∵DH⊥AB,
∴BH=EH,
在Rt△BEK中,HK=BE=HB=EH,
∴∠HKE=∠HEK,
∴∠HKF=∠GCF,
∵MF⊥DC,MK=MC,
∴FK=CF,
在△HFK和△GFC中,
,
∴△HFK≌△GFC(ASA),
∴FH=FG;
(3)解:如图3,过点G作GP∥AB交DC于点P,连接EM,
∵GP∥AB,
∴∠EHF=∠PGF,
∵FH=FG,∠EFH=∠PFG,
∴△FHE≌△FGP(ASA),
∴EF=PF=EP,
∵△HFK≌△GFC,
∴HK=CG,
∵HK=HB=HE,
∴CG=HB=HE,
∵3AG=2BH,
∴=,
∵GP∥AE,
∴==,
∵EF=PF,
∴EF=EC,
∵EF=2,
∴EC=10,
∵BC=2CE,MB=MC,
∴MC=MB=CE=10,
∴∠CEM=∠CME,
过点E作EQ⊥BC于点Q,
∵EQ⊥BC,
∴∠EQC=∠EQB=∠MFE=90°,
∵EM=ME,
∴△EFM≌△MQE(AAS),
∴MQ=EF=2,
∴CF=CQ=10﹣2=8,
在Rt△MFC中,由勾股定理得:FM2+FC2=MC2,
即FM2+82=102,
解得:FM=6(负值已舍去),
∴EQ=6,
∴tan∠ECQ===,
∵BQ=BM+MQ=10+2=12,
∴tan∠EBQ===,
∴BE===6,
取EC的中点T,连接AT,过点C作CR⊥AB于点R,
∵∠AEC=∠ACE,
∴AE=AC,
∵TE=TC,
∴AT⊥DC,∠EAT=∠CAT,
∵tan∠CBR=,BC=20,
∴BR=2CR,
由勾股定理得:CR==,
解得:CR=4,
∴BR=8,
∴ER=BR﹣BE=8﹣6=2,
∴tan∠REC===2,
∴tan∠EAT=tan∠CAT=,
∵tan∠ADC=tan∠ABC==,
∴tan∠CAT=tan∠ADC=,
设AT=2k,
∴DT=2AT=4k,TC=k,
∴DC=5k,
∵tan∠CAT=tan∠ADC,
∴∠CAT=∠ADC,
∵∠CAT+∠ACD=90°,
∴∠ADC+∠ACD=90°,
∴∠DAC=90°,
∴DC为直径,
∵EC=10,
∴ET=CT=5,
∵DC=5TC,
∴DC=25,
∴⊙O的直径为25.
26.在平面直角坐标系中,O为坐标原点,直线AB交x轴的正半轴于点A(6,0),交y轴的负半轴于点B,且tan∠.
(1)如图1,求直线AB的解析式;
(2)如图2,P为线段AB上一点,点C的坐标为,连接CP,设点P的横坐标为t,△BCP的面积为S,求S与t的函数关系式;(不需要写出自变量t的取值范围);
(3)如图3,在(2)的条件下,点D的坐标为,点E、F都在y轴的负半轴上,且点E在点F的上方,连接DE、AC、AE、AF,且∠EDO=∠ACO,若AE平分∠BAF,AF=2AP,连接FP交AE于点G,求点G的坐标.
【解答】解:(1)∵∠AOB=90°,
∴tan∠OAB=,
∵A(6,0),
∴OA=6,
∴OB=,
∴B(0,﹣),
设直线AB的解析式为:y=kx+b,
∴,
∴,
∴y=﹣;
(2)∵C,B(0,﹣),
∴BC=,
∴S△BCP=BC xP=,
∴S=;
(3)如图,
作PQ⊥OA于Q,
∵∠AOC=∠DOE,∠EDO=∠ACO,
∴△AOC∽△EOD,
∴,
∴,
∴OE=2,
∴BE=OE﹣OB=,
∵AE平分∠BAF,
∴,
∴,
∴,
设EF=m,则AF=m,
在Rt△AOF中,OA=6,OF=OE+EF=m+2,AF=m,
∴62+(m+2)2=(m)2,
m1=,m2=﹣(舍去),
∴AF=,
∴AP=AF=,
∵PQ∥OB,
∴△APQ∽△ABO,
∴,
∴=,
∴AQ=4,PQ=,
∴OQ=2,
∴P(2,﹣),
∵F(0,﹣),
∴直线PF的解析式为:y=x﹣,
∵A(6,0),E(0,﹣2),
∴y=x﹣2,
由得,
x=,
当x=时,y==﹣,
∴G(,﹣).
第1页(共1页)
同课章节目录
