黑龙江省哈尔滨市香坊区风华中学2023-2024学年七年级(上)开学数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市香坊区风华中学2023-2024学年七年级(上)开学数学试卷(五四学制)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 09:56:57 | ||
图片预览




文档简介
2023-2024学年黑龙江省哈尔滨市香坊区风华中学七年级(上)开学数学试卷(五四学制)
一、选择题(每小题3分,共计24分)
1.(3分)2023的相反数等于( )
A.2023 B.﹣2023 C. D.
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.3ab﹣2ba=ab
C.3a2b﹣3ab2=0 D.2a2+3a3=5a5
3.(3分)在有理数:,2,0,﹣1中,最小的数是( )
A.﹣1 B. C.0 D.2
4.(3分)如图所示的几何体是由五个小正方体组合而成的,它的俯视图是( )
A. B.
C. D.
5.(3分)有理数a、b在数轴上的位置如图所示,以下说法正确的是( )
A.b<a B.ab>0 C.a+b>0 D.a﹣b<0
6.(3分)以下调查中,适合抽样调查的是( )
A.了解某班学生的身高情况
B.调查池塘中现有鱼的数量
C.全国人口普查
D.对与新冠肺炎患者乘同一航班的旅客进行医学检查
7.(3分)把三角板按如图所示那样拼在一起,则∠CAD=( )
A.30° B.45° C.25° D.60°
8.(3分)如图,一艘轮船行驶到B处时,测得小岛A、C的方向分别为北偏西30°17′和西南方向,则∠ABC的度数是( )
A.75°17′ B.75°43′ C.104°17′ D.104°43′
二、填空题(每小题3分,共计24分)
9.(3分)中国的领水面积约为370000km2,将数370000用科学记数法表示为 .
10.(3分)﹣的绝对值是 .
11.(3分)单项式﹣的次数是 .
12.(3分)多项式x2﹣2kxy﹣5y2+2xy﹣6合并同类项后不含xy项,则k的值是 .
13.(3分)9点30分,钟表的时针与分针所夹的角度是 .
14.(3分)端午将至,某食品超市购进一种新口味粽子,每盒成本a元,按每盒加价b元后进行标价,然后面向消费者打出“八折”出售的销售方案,短短一天,已销售80盒,则这家超市这一天销售这80盒粽子所获利润为 元.
15.(3分)观察下列图形:它们是按一定规律排列的,依此规律,第7个图形共有 个★.
16.(3分)在同一平面内,∠AOB=25°,∠AOC与∠AOB互余,则∠COB为 °.
三、解答题(共52分,期中17题12分,18-21题每题10分)
17.(12分)计算:
(1)4+(﹣2)2×5﹣(﹣8)÷4;
(2).
18.(10分)先化简,后求值:x﹣2(x﹣y2)+(﹣x+),其中x=﹣2,y=.
19.(10分)如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
20.(10分)超市购进8筐白菜,以每筐25kg为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,﹣3,2,﹣0.5,1,﹣2,﹣2,﹣2.5.
(1)这8筐白菜总计超过或不足多少千克?
(2)这8筐白菜一共多少千克?
(3)超市计划这8筐白菜按每千克3元销售,为促销超市决定打九折销售,求这8筐白菜现价比原价便宜了多少钱?
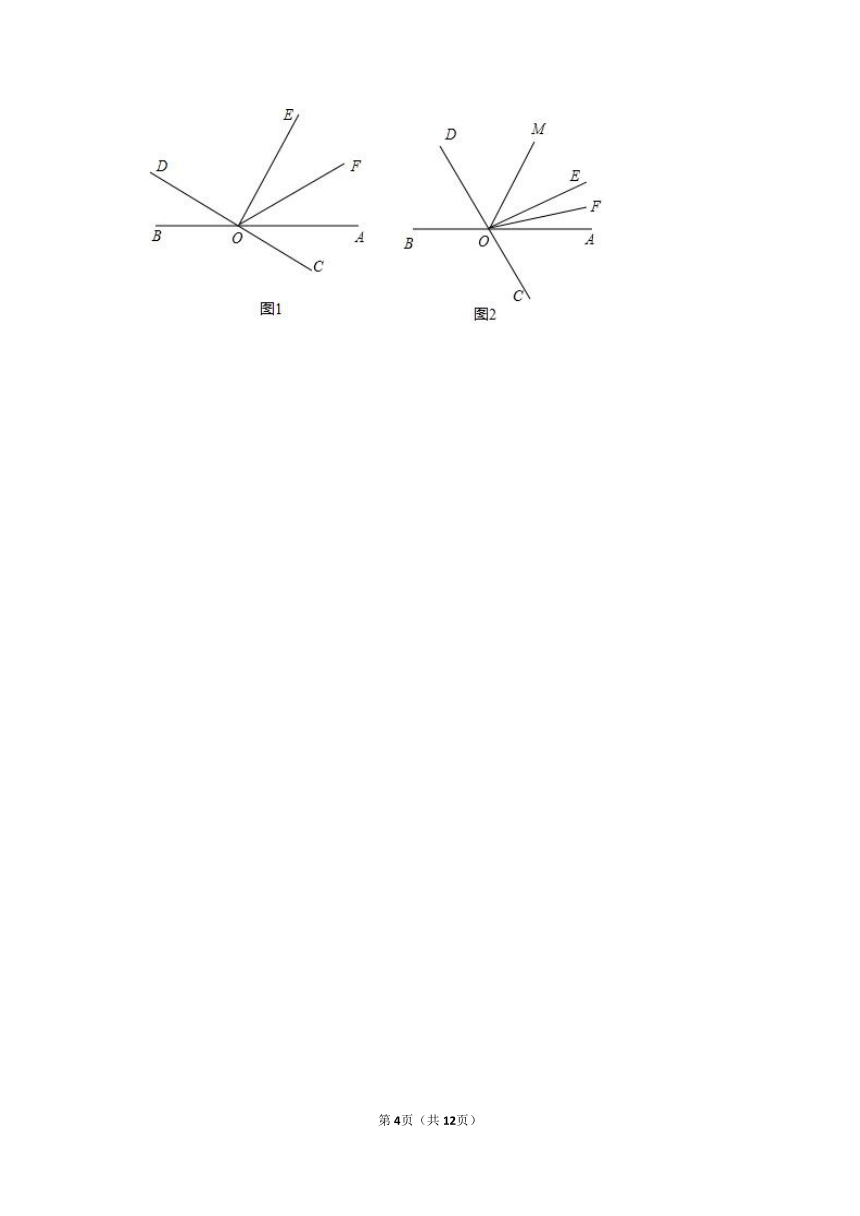
21.(10分)直线AB、CD相交于点O,∠EOF在∠AOD的内部.
(1)如图①,当∠AOD=150°,∠EOF=30°时,求∠AOF与∠EOD的度数和;
(2)在(1)的条件下,请直接写出图中与∠BOC互补的角;
(3)如图②,若射线OM平分∠AOD(OM在∠EOD内部),且满足∠EOD=2∠FOM,请判断∠AOF与∠EOF的大小关系并说明理由.
2023-2024学年黑龙江省哈尔滨市香坊区风华中学七年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计24分)
1.(3分)2023的相反数等于( )
A.2023 B.﹣2023 C. D.
【解答】解:2023的相反数等于﹣2023.
故选:B.
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.3ab﹣2ba=ab
C.3a2b﹣3ab2=0 D.2a2+3a3=5a5
【解答】解:∵2a和3b不是同类项,
∴选项A不符合题意;
∵3ab﹣2ba=ab,
∴选项B符合题意;
∵3a2b和3ab2不是同类项,
∴选项C不符合题意;
∵2a2和3a3不是同类项,
∴选项D不符合题意,
故选:B.
3.(3分)在有理数:,2,0,﹣1中,最小的数是( )
A.﹣1 B. C.0 D.2
【解答】解:2,0是正数,,﹣1是负数,
又,
因此﹣1最小,
故选:A.
4.(3分)如图所示的几何体是由五个小正方体组合而成的,它的俯视图是( )
A. B.
C. D.
【解答】解:从上面看共有3列,从左到右小正方形的个数分别为2、1、1,
故选:C.
5.(3分)有理数a、b在数轴上的位置如图所示,以下说法正确的是( )
A.b<a B.ab>0 C.a+b>0 D.a﹣b<0
【解答】解:根据题意可得:a<0<b,|a|>|b|,
∴b>a,ab<0,a+b<0,a﹣b<0,
纵观各选项,只有D选项符合题意;
故选:D.
6.(3分)以下调查中,适合抽样调查的是( )
A.了解某班学生的身高情况
B.调查池塘中现有鱼的数量
C.全国人口普查
D.对与新冠肺炎患者乘同一航班的旅客进行医学检查
【解答】解:A、了解某班学生的身高情况,适宜采用全面调查方式,故本选项不符合题意;
B、调查池塘中现有鱼的数量,适宜采用抽样调查方式,故本选项符合题意;
C、全国人口普查,适宜采用全面调查方式,故本选项不符合题意;
D、对与新冠肺炎患者乘同一航班的旅客进行医学检查,适宜采用全面调查方式,故本选项不符合题意;
故选:B.
7.(3分)把三角板按如图所示那样拼在一起,则∠CAD=( )
A.30° B.45° C.25° D.60°
【解答】解:由题意得:∠BAD=90°,∠CAB=60°,
∴∠CAD=∠BAD﹣∠CAB=90°﹣60°=30°,
故选:A.
8.(3分)如图,一艘轮船行驶到B处时,测得小岛A、C的方向分别为北偏西30°17′和西南方向,则∠ABC的度数是( )
A.75°17′ B.75°43′ C.104°17′ D.104°43′
【解答】解:根据题意可得:∠DBA=30°17′,∠EBC=45°,
∴∠ABC=180°﹣45°﹣30°17′=104°43′;
故选:D.
二、填空题(每小题3分,共计24分)
9.(3分)中国的领水面积约为370000km2,将数370000用科学记数法表示为 3.7×105 .
【解答】解:370 000=3.7×105,
故答案为:3.7×105.
10.(3分)﹣的绝对值是 .
【解答】解:根据负数的绝对值等于它的相反数,得||=.
11.(3分)单项式﹣的次数是 7 .
【解答】解:单项式﹣的次数是:7,
故答案为:7.
12.(3分)多项式x2﹣2kxy﹣5y2+2xy﹣6合并同类项后不含xy项,则k的值是 1 .
【解答】解:x2﹣2kxy﹣5y2+2xy﹣6
=x2+(2﹣2k)xy﹣5y2﹣6,
∵多项式x2﹣2kxy﹣5y2+2xy﹣6合并同类项后不含xy项,
∴2﹣2k=0,
2k=2,
∴k=1,
故答案为:1.
13.(3分)9点30分,钟表的时针与分针所夹的角度是 105° .
【解答】解:根据题意得,9点30分,钟表的时针与分针所夹的角度为:3.5×30=105°,
故答案为105°.
14.(3分)端午将至,某食品超市购进一种新口味粽子,每盒成本a元,按每盒加价b元后进行标价,然后面向消费者打出“八折”出售的销售方案,短短一天,已销售80盒,则这家超市这一天销售这80盒粽子所获利润为 (64b﹣16a) 元.
【解答】解:这家超市这一天销售这80盒粽子所获利润为[80×80%(b+a)﹣80a]=(64b+64a﹣80a)=(64b﹣16a)元;
故答案为:(64b﹣16a).
15.(3分)观察下列图形:它们是按一定规律排列的,依此规律,第7个图形共有 18 个★.
【解答】解:设第n个图形中共有an个★(n为正整数).
观察图形,可知:a1=2×3﹣1+1=6,a2=2×4﹣1+1=8,a3=2×5﹣1+1=10,…,
∴an=2n+4(n为正整数),
∴a7=2×7+4=18.
故答案为:18.
16.(3分)在同一平面内,∠AOB=25°,∠AOC与∠AOB互余,则∠COB为 90或40 °.
【解答】解:①如图1,OC在AO上面,
∵∠AOB=25°,∠AOC与∠AOB互余,
∴∠AOC=65°,
∴∠COB=90°;
②如图2,OC在AO下面,
∵∠AOB=25°,∠AOC与∠AOB互余,
∴∠AOC=90°﹣25°=65°,
∴∠COB=65°﹣25°=40°;
综上所述,∠AOC的度数是90°或40°.
故答案为:90或40.
三、解答题(共52分,期中17题12分,18-21题每题10分)
17.(12分)计算:
(1)4+(﹣2)2×5﹣(﹣8)÷4;
(2).
【解答】解:(1)原式=4+4×5﹣(﹣2)
=4+20+2
=26;
(2)原式=﹣36×﹣(﹣36)×﹣(﹣36)×
=﹣16+30+21
=35.
18.(10分)先化简,后求值:x﹣2(x﹣y2)+(﹣x+),其中x=﹣2,y=.
【解答】解:原式=x﹣2x+y2﹣x+y2=﹣x+y2,
当x=﹣2,y=时,原式=+=.
19.(10分)如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
【解答】解:(1)线段AB=20,BC=15,
∴AC=AB﹣BC=20﹣15=5.
又∵点M是AC的中点.
∴AM=AC=×5=,即线段AM的长度是.
(2)∵BC=15,CN:NB=2:3,
∴CN=BC=×15=6.
又∵点M是AC的中点,AC=5,
∴MC=AC=,
∴MN=MC+NC=,即MN的长度是.
20.(10分)超市购进8筐白菜,以每筐25kg为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,﹣3,2,﹣0.5,1,﹣2,﹣2,﹣2.5.
(1)这8筐白菜总计超过或不足多少千克?
(2)这8筐白菜一共多少千克?
(3)超市计划这8筐白菜按每千克3元销售,为促销超市决定打九折销售,求这8筐白菜现价比原价便宜了多少钱?
【解答】解:(1)1.5﹣3+2﹣0.5+1﹣2﹣2﹣2.5=﹣5.5(千克),
答:以每筐25千克为标准,这8筐白菜总计不足5.5千克;
(2)1.5﹣3+2﹣0.5+1﹣2﹣2﹣2.5=﹣5.5(千克),
25×8﹣5.5=194.5(千克),
答:这8筐白菜一共194.5千克;
(3)194.5×3=583.5(元),
583.5×(1﹣0.9)=58.35(元).
答:这8筐白菜现价比原价便宜了58.35元.
21.(10分)直线AB、CD相交于点O,∠EOF在∠AOD的内部.
(1)如图①,当∠AOD=150°,∠EOF=30°时,求∠AOF与∠EOD的度数和;
(2)在(1)的条件下,请直接写出图中与∠BOC互补的角;
(3)如图②,若射线OM平分∠AOD(OM在∠EOD内部),且满足∠EOD=2∠FOM,请判断∠AOF与∠EOF的大小关系并说明理由.
【解答】解:(1)∵∠DOE+∠EOF+∠AOF=∠AOD=150°且∠EOF=30°,
∴∠DOE+∠AOF=∠150°﹣30°=120°;
(2)根据补角的定义可知图中与∠BOC互补的角有∠BOD、∠AOC、∠EOF;
(3)∠AOF=∠EOF,理由如下:
∵OM平分∠AOD,
∴∠DOM=∠AOM,
∴∠AOF=∠AOM﹣∠FOM
=∠DOM﹣∠FOM
=∠EOD﹣∠MOE﹣∠FOM
=2∠FOM﹣∠MOE﹣∠FOM
=∠FOM﹣∠MOE
=∠EOF,
∴∠AOF=∠EOF.
第1页(共1页)
一、选择题(每小题3分,共计24分)
1.(3分)2023的相反数等于( )
A.2023 B.﹣2023 C. D.
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.3ab﹣2ba=ab
C.3a2b﹣3ab2=0 D.2a2+3a3=5a5
3.(3分)在有理数:,2,0,﹣1中,最小的数是( )
A.﹣1 B. C.0 D.2
4.(3分)如图所示的几何体是由五个小正方体组合而成的,它的俯视图是( )
A. B.
C. D.
5.(3分)有理数a、b在数轴上的位置如图所示,以下说法正确的是( )
A.b<a B.ab>0 C.a+b>0 D.a﹣b<0
6.(3分)以下调查中,适合抽样调查的是( )
A.了解某班学生的身高情况
B.调查池塘中现有鱼的数量
C.全国人口普查
D.对与新冠肺炎患者乘同一航班的旅客进行医学检查
7.(3分)把三角板按如图所示那样拼在一起,则∠CAD=( )
A.30° B.45° C.25° D.60°
8.(3分)如图,一艘轮船行驶到B处时,测得小岛A、C的方向分别为北偏西30°17′和西南方向,则∠ABC的度数是( )
A.75°17′ B.75°43′ C.104°17′ D.104°43′
二、填空题(每小题3分,共计24分)
9.(3分)中国的领水面积约为370000km2,将数370000用科学记数法表示为 .
10.(3分)﹣的绝对值是 .
11.(3分)单项式﹣的次数是 .
12.(3分)多项式x2﹣2kxy﹣5y2+2xy﹣6合并同类项后不含xy项,则k的值是 .
13.(3分)9点30分,钟表的时针与分针所夹的角度是 .
14.(3分)端午将至,某食品超市购进一种新口味粽子,每盒成本a元,按每盒加价b元后进行标价,然后面向消费者打出“八折”出售的销售方案,短短一天,已销售80盒,则这家超市这一天销售这80盒粽子所获利润为 元.
15.(3分)观察下列图形:它们是按一定规律排列的,依此规律,第7个图形共有 个★.
16.(3分)在同一平面内,∠AOB=25°,∠AOC与∠AOB互余,则∠COB为 °.
三、解答题(共52分,期中17题12分,18-21题每题10分)
17.(12分)计算:
(1)4+(﹣2)2×5﹣(﹣8)÷4;
(2).
18.(10分)先化简,后求值:x﹣2(x﹣y2)+(﹣x+),其中x=﹣2,y=.
19.(10分)如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
20.(10分)超市购进8筐白菜,以每筐25kg为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,﹣3,2,﹣0.5,1,﹣2,﹣2,﹣2.5.
(1)这8筐白菜总计超过或不足多少千克?
(2)这8筐白菜一共多少千克?
(3)超市计划这8筐白菜按每千克3元销售,为促销超市决定打九折销售,求这8筐白菜现价比原价便宜了多少钱?
21.(10分)直线AB、CD相交于点O,∠EOF在∠AOD的内部.
(1)如图①,当∠AOD=150°,∠EOF=30°时,求∠AOF与∠EOD的度数和;
(2)在(1)的条件下,请直接写出图中与∠BOC互补的角;
(3)如图②,若射线OM平分∠AOD(OM在∠EOD内部),且满足∠EOD=2∠FOM,请判断∠AOF与∠EOF的大小关系并说明理由.
2023-2024学年黑龙江省哈尔滨市香坊区风华中学七年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计24分)
1.(3分)2023的相反数等于( )
A.2023 B.﹣2023 C. D.
【解答】解:2023的相反数等于﹣2023.
故选:B.
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.3ab﹣2ba=ab
C.3a2b﹣3ab2=0 D.2a2+3a3=5a5
【解答】解:∵2a和3b不是同类项,
∴选项A不符合题意;
∵3ab﹣2ba=ab,
∴选项B符合题意;
∵3a2b和3ab2不是同类项,
∴选项C不符合题意;
∵2a2和3a3不是同类项,
∴选项D不符合题意,
故选:B.
3.(3分)在有理数:,2,0,﹣1中,最小的数是( )
A.﹣1 B. C.0 D.2
【解答】解:2,0是正数,,﹣1是负数,
又,
因此﹣1最小,
故选:A.
4.(3分)如图所示的几何体是由五个小正方体组合而成的,它的俯视图是( )
A. B.
C. D.
【解答】解:从上面看共有3列,从左到右小正方形的个数分别为2、1、1,
故选:C.
5.(3分)有理数a、b在数轴上的位置如图所示,以下说法正确的是( )
A.b<a B.ab>0 C.a+b>0 D.a﹣b<0
【解答】解:根据题意可得:a<0<b,|a|>|b|,
∴b>a,ab<0,a+b<0,a﹣b<0,
纵观各选项,只有D选项符合题意;
故选:D.
6.(3分)以下调查中,适合抽样调查的是( )
A.了解某班学生的身高情况
B.调查池塘中现有鱼的数量
C.全国人口普查
D.对与新冠肺炎患者乘同一航班的旅客进行医学检查
【解答】解:A、了解某班学生的身高情况,适宜采用全面调查方式,故本选项不符合题意;
B、调查池塘中现有鱼的数量,适宜采用抽样调查方式,故本选项符合题意;
C、全国人口普查,适宜采用全面调查方式,故本选项不符合题意;
D、对与新冠肺炎患者乘同一航班的旅客进行医学检查,适宜采用全面调查方式,故本选项不符合题意;
故选:B.
7.(3分)把三角板按如图所示那样拼在一起,则∠CAD=( )
A.30° B.45° C.25° D.60°
【解答】解:由题意得:∠BAD=90°,∠CAB=60°,
∴∠CAD=∠BAD﹣∠CAB=90°﹣60°=30°,
故选:A.
8.(3分)如图,一艘轮船行驶到B处时,测得小岛A、C的方向分别为北偏西30°17′和西南方向,则∠ABC的度数是( )
A.75°17′ B.75°43′ C.104°17′ D.104°43′
【解答】解:根据题意可得:∠DBA=30°17′,∠EBC=45°,
∴∠ABC=180°﹣45°﹣30°17′=104°43′;
故选:D.
二、填空题(每小题3分,共计24分)
9.(3分)中国的领水面积约为370000km2,将数370000用科学记数法表示为 3.7×105 .
【解答】解:370 000=3.7×105,
故答案为:3.7×105.
10.(3分)﹣的绝对值是 .
【解答】解:根据负数的绝对值等于它的相反数,得||=.
11.(3分)单项式﹣的次数是 7 .
【解答】解:单项式﹣的次数是:7,
故答案为:7.
12.(3分)多项式x2﹣2kxy﹣5y2+2xy﹣6合并同类项后不含xy项,则k的值是 1 .
【解答】解:x2﹣2kxy﹣5y2+2xy﹣6
=x2+(2﹣2k)xy﹣5y2﹣6,
∵多项式x2﹣2kxy﹣5y2+2xy﹣6合并同类项后不含xy项,
∴2﹣2k=0,
2k=2,
∴k=1,
故答案为:1.
13.(3分)9点30分,钟表的时针与分针所夹的角度是 105° .
【解答】解:根据题意得,9点30分,钟表的时针与分针所夹的角度为:3.5×30=105°,
故答案为105°.
14.(3分)端午将至,某食品超市购进一种新口味粽子,每盒成本a元,按每盒加价b元后进行标价,然后面向消费者打出“八折”出售的销售方案,短短一天,已销售80盒,则这家超市这一天销售这80盒粽子所获利润为 (64b﹣16a) 元.
【解答】解:这家超市这一天销售这80盒粽子所获利润为[80×80%(b+a)﹣80a]=(64b+64a﹣80a)=(64b﹣16a)元;
故答案为:(64b﹣16a).
15.(3分)观察下列图形:它们是按一定规律排列的,依此规律,第7个图形共有 18 个★.
【解答】解:设第n个图形中共有an个★(n为正整数).
观察图形,可知:a1=2×3﹣1+1=6,a2=2×4﹣1+1=8,a3=2×5﹣1+1=10,…,
∴an=2n+4(n为正整数),
∴a7=2×7+4=18.
故答案为:18.
16.(3分)在同一平面内,∠AOB=25°,∠AOC与∠AOB互余,则∠COB为 90或40 °.
【解答】解:①如图1,OC在AO上面,
∵∠AOB=25°,∠AOC与∠AOB互余,
∴∠AOC=65°,
∴∠COB=90°;
②如图2,OC在AO下面,
∵∠AOB=25°,∠AOC与∠AOB互余,
∴∠AOC=90°﹣25°=65°,
∴∠COB=65°﹣25°=40°;
综上所述,∠AOC的度数是90°或40°.
故答案为:90或40.
三、解答题(共52分,期中17题12分,18-21题每题10分)
17.(12分)计算:
(1)4+(﹣2)2×5﹣(﹣8)÷4;
(2).
【解答】解:(1)原式=4+4×5﹣(﹣2)
=4+20+2
=26;
(2)原式=﹣36×﹣(﹣36)×﹣(﹣36)×
=﹣16+30+21
=35.
18.(10分)先化简,后求值:x﹣2(x﹣y2)+(﹣x+),其中x=﹣2,y=.
【解答】解:原式=x﹣2x+y2﹣x+y2=﹣x+y2,
当x=﹣2,y=时,原式=+=.
19.(10分)如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
【解答】解:(1)线段AB=20,BC=15,
∴AC=AB﹣BC=20﹣15=5.
又∵点M是AC的中点.
∴AM=AC=×5=,即线段AM的长度是.
(2)∵BC=15,CN:NB=2:3,
∴CN=BC=×15=6.
又∵点M是AC的中点,AC=5,
∴MC=AC=,
∴MN=MC+NC=,即MN的长度是.
20.(10分)超市购进8筐白菜,以每筐25kg为准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,﹣3,2,﹣0.5,1,﹣2,﹣2,﹣2.5.
(1)这8筐白菜总计超过或不足多少千克?
(2)这8筐白菜一共多少千克?
(3)超市计划这8筐白菜按每千克3元销售,为促销超市决定打九折销售,求这8筐白菜现价比原价便宜了多少钱?
【解答】解:(1)1.5﹣3+2﹣0.5+1﹣2﹣2﹣2.5=﹣5.5(千克),
答:以每筐25千克为标准,这8筐白菜总计不足5.5千克;
(2)1.5﹣3+2﹣0.5+1﹣2﹣2﹣2.5=﹣5.5(千克),
25×8﹣5.5=194.5(千克),
答:这8筐白菜一共194.5千克;
(3)194.5×3=583.5(元),
583.5×(1﹣0.9)=58.35(元).
答:这8筐白菜现价比原价便宜了58.35元.
21.(10分)直线AB、CD相交于点O,∠EOF在∠AOD的内部.
(1)如图①,当∠AOD=150°,∠EOF=30°时,求∠AOF与∠EOD的度数和;
(2)在(1)的条件下,请直接写出图中与∠BOC互补的角;
(3)如图②,若射线OM平分∠AOD(OM在∠EOD内部),且满足∠EOD=2∠FOM,请判断∠AOF与∠EOF的大小关系并说明理由.
【解答】解:(1)∵∠DOE+∠EOF+∠AOF=∠AOD=150°且∠EOF=30°,
∴∠DOE+∠AOF=∠150°﹣30°=120°;
(2)根据补角的定义可知图中与∠BOC互补的角有∠BOD、∠AOC、∠EOF;
(3)∠AOF=∠EOF,理由如下:
∵OM平分∠AOD,
∴∠DOM=∠AOM,
∴∠AOF=∠AOM﹣∠FOM
=∠DOM﹣∠FOM
=∠EOD﹣∠MOE﹣∠FOM
=2∠FOM﹣∠MOE﹣∠FOM
=∠FOM﹣∠MOE
=∠EOF,
∴∠AOF=∠EOF.
第1页(共1页)
同课章节目录
