黑龙江省哈尔滨市香坊区风华中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市香坊区风华中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 09:57:07 | ||
图片预览



文档简介
2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)开学数学试卷(五四学制)
一、选择题(每小题3分,共30分)
1.(3分)下列方程中,是一元二次方程的是( )
A. B.x2﹣4=4
C.5x2+3x﹣2y=0 D.x﹣5=0
2.(3分)下列三角形中,不是直角三角形的是( )
A.三条边长之比为
B.三条边长之比为
C.三条边长之比为5:12:13
D.三个角度数之比为1:3:4
3.(3分)在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( )
A. B.2 C. D.
4.(3分)能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
5.(3分)如图,身高1.6m的小亮站在某路灯下,发现自己的影长恰好是3m,经测量,此时小亮离路灯底部的距离是9m,则路灯离地面的高度AB是( )
A.4.8m B.6m C.6.4m D.9m
6.(3分)如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50°,测得BC=60m,则桥长AB=( )m.
A. B.60 cos50° C. D.60 tan50°
7.(3分)点A(3,y1)和点B(﹣2,y2)都在直线y=﹣2x+3上,则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
8.(3分)如图,AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
9.(3分)某商店购入一批衬衫进行销售,当每件盈利30元,每星期可以卖出100件,现需降价处理:每件衬衫售价每降价5元,每星期可以多卖出20个,店里每星期衬衫的利润要达到2800元.若设每件衬衫售价降低x元,则可列方程为( )
A.(30+x)(100﹣20x)=2800
B.(30+x)(100﹣4x)=2800
C.(30﹣x)(100+20x)=2800
D.(30﹣x)(100+4x)=2800
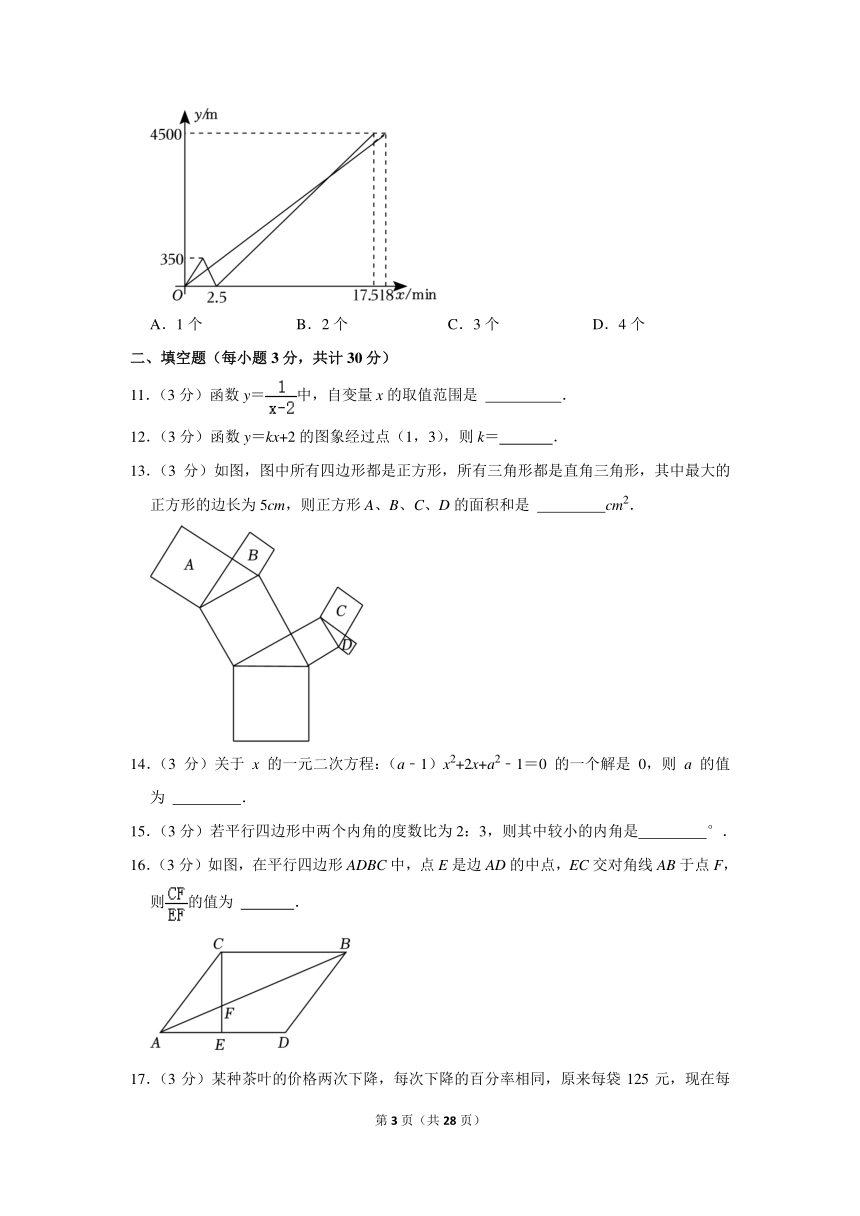
10.(3分)周末小晨、小亮相约进行长跑比赛,两人同时起跑,刚跑出350米,小亮发现重要物品落在出发地,立刻原速返回,取回后以更快的速度投入比赛,若他们距离出发地y(m)与比赛时间x(min)的关系如图,下列说法正确的个数有( )
(1)小亮共跑了5200m;
(2)小晨全程的平均速度为250m/min;
(3)两人起跑以后第一次相遇时间为;
(4)小亮再次投入比赛后在距离终点750m时追上了小晨.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计30分)
11.(3分)函数y=中,自变量x的取值范围是 .
12.(3分)函数y=kx+2的图象经过点(1,3),则k= .
13.(3分)如图,图中所有四边形都是正方形,所有三角形都是直角三角形,其中最大的正方形的边长为5cm,则正方形A、B、C、D的面积和是 cm2.
14.(3分)关于x的一元二次方程:(a﹣1)x2+2x+a2﹣1=0的一个解是0,则a的值为 .
15.(3分)若平行四边形中两个内角的度数比为2:3,则其中较小的内角是 °.
16.(3分)如图,在平行四边形ADBC中,点E是边AD的中点,EC交对角线AB于点F,则的值为 .
17.(3分)某种茶叶的价格两次下降,每次下降的百分率相同,原来每袋125元,现在每袋80元,则每次下降的百分率是 .
18.(3分)如图,正方形ABCD,∠EAF=45°,∠EAF的两边分别交边BC,DC于点E、F,若BE=2,DF=3,则AF的长为 .
19.(3分)已知△ABC中,D、E分别是AB、AC的中点,F为直线BC上一点,EF=BC,∠EFC=50°,则∠EDF= 度.
20.(3分)如图,在Rt△ACB中,∠C=90°,点D为BC上一点,过点B作AD的垂线交AD的延长线于点E,若∠ABD+∠CDA=90°,4AD=5DE,,则线段BD的长为 .
三、解答题:(21、22题每题7分;23、24题每题8分;25、26、27题每题10分)
21.(7分)先化简,再求的值,其中a=4cos30°﹣2tan45°.
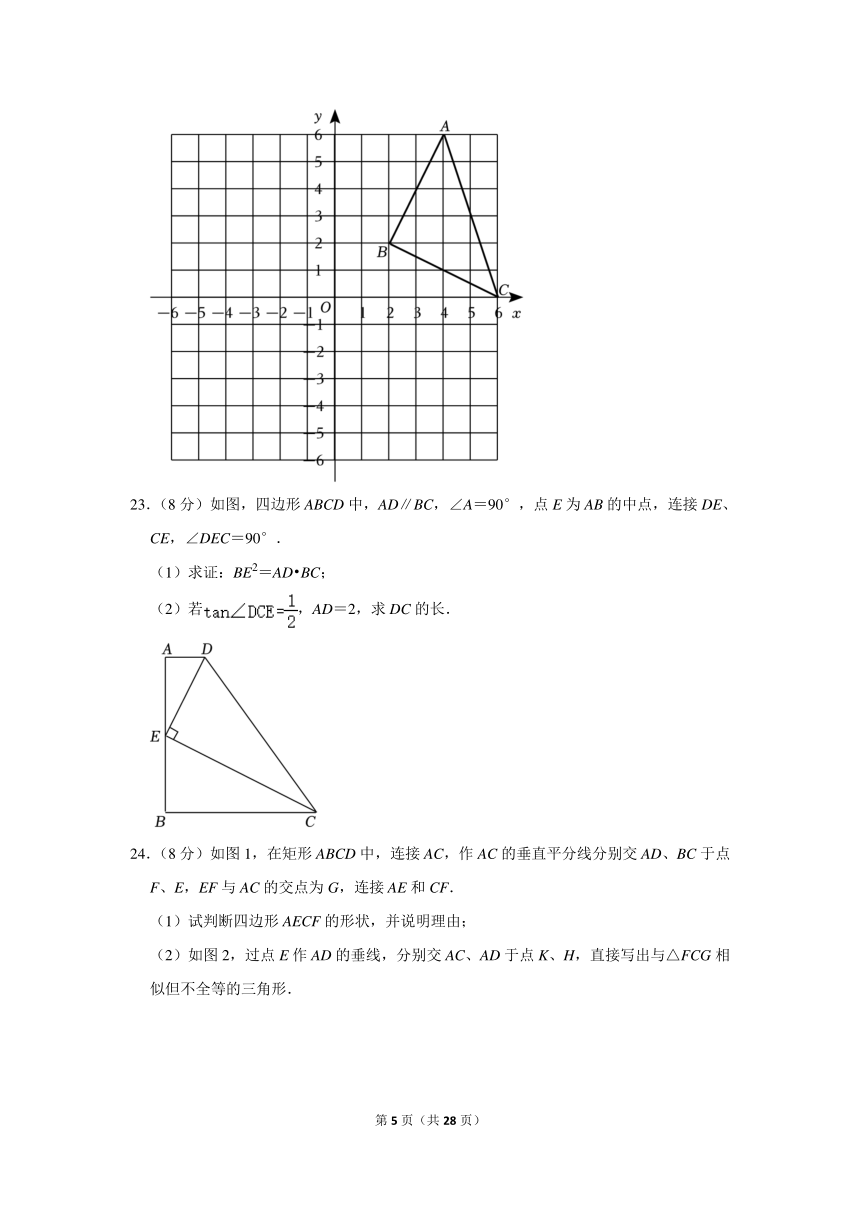
22.(7分)△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在小正方形的顶点上,每个小正方形边长均为1.
(1)以原点O为位似中心,在第三象限画出△A1B1C1,使△A1B1C1与△ABC的相似比为1:2;
(2)作出△ABC关于y轴对称的△A2B2C2;连接A2B,B2B,并直接写出∠A2BB2的正切值.
23.(8分)如图,四边形ABCD中,AD∥BC,∠A=90°,点E为AB的中点,连接DE、CE,∠DEC=90°.
(1)求证:BE2=AD BC;
(2)若,AD=2,求DC的长.
24.(8分)如图1,在矩形ABCD中,连接AC,作AC的垂直平分线分别交AD、BC于点F、E,EF与AC的交点为G,连接AE和CF.
(1)试判断四边形AECF的形状,并说明理由;
(2)如图2,过点E作AD的垂线,分别交AC、AD于点K、H,直接写出与△FCG相似但不全等的三角形.
25.(10分)2023年哈尔滨马拉松比赛召开期间,某体育用品商店迎合市场热度,计划购进A、B种两种品牌的跑步鞋,若购进4双A品牌跑步鞋和3双B品牌跑步鞋,需要3200元,若购进3双A品牌跑步鞋和2双B品牌跑步鞋,需要2300元.
(1)求该商店购进A、B两种品牌跑步鞋的单价分别是多少?
(2)若商店共购进两种跑步鞋60双,且A品牌跑鞋的数量不多于B品牌跑步鞋的,如果这两种跑步鞋每双均加价20%出售,当购进A品牌跑步鞋多少双时,商店获得的总利润W最大,总利润W最大是多少?
26.(10分)在△ABC中,AB=AC,点D在线段CB的延长线上,连接AD,过点B作BE⊥BC交线段AD于点E,2∠BED+∠BAC=120°.
(1)如图1,求∠CAD的度数;
(2)如图2,若,求的值;
(3)如图3,在(2)的条件下,连接EC,EC交线段AB于点F,若BD=3,求AF的长.
27.(10分)在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,C,过点C作CD∥OA交AB于点D,连接OD.
(1)如图1,求∠ADO的度数;
(2)如图2,点P在射线AO上(点P不与点A重合),过点P作PQ⊥AB,垂足为点Q,若AP=m,DQ=n,求出n与m的函数关系式,并直接写出m的取值范围;
(3)如图3,在(2)的条件下,当DQ=3时,连接OQ,在射线QA上是否存在点K,连接OK,使△OQK为等腰三角形,若存在,求出AK的长.
2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列方程中,是一元二次方程的是( )
A. B.x2﹣4=4
C.5x2+3x﹣2y=0 D.x﹣5=0
【解答】解:A、是分式方程,不符合题意;
B、x2﹣4=4是一元二次方程,符合题意;
C、5x2+3x﹣2y=0是二元二次方程,不符合题意;
D、x﹣5=0是一元一次方程,不符合题意.
故选:B.
2.(3分)下列三角形中,不是直角三角形的是( )
A.三条边长之比为
B.三条边长之比为
C.三条边长之比为5:12:13
D.三个角度数之比为1:3:4
【解答】解:A、()2+()2≠()2,不能作为直角三角形的三边长,故本选项符合题意;
B、12+22=()2,能作为直角三角形的三边长,故本选项不符合题意;
C、52+122=132,能作为直角三角形的三边长,故本选项符不合题意;
D、180°×=90°,是直角三角形,故此选项不合题意;
故选:A.
3.(3分)在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( )
A. B.2 C. D.
【解答】解:根据题意,AB==BC,sinA===.
故选:C.
4.(3分)能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
【解答】解:根据平行四边形的判定定理知,A、B、D均不符合是平行四边形的条件;
C满足两组对边分别相等的四边形是平行四边形.
故选:C.
5.(3分)如图,身高1.6m的小亮站在某路灯下,发现自己的影长恰好是3m,经测量,此时小亮离路灯底部的距离是9m,则路灯离地面的高度AB是( )
A.4.8m B.6m C.6.4m D.9m
【解答】解:如图,AD=9m,DE=3m,CD=1.8m,
∵CD∥AB,
∴△EDC∽△EAB,
∴=,即,
∴AB=6.4m.
故选:C.
6.(3分)如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50°,测得BC=60m,则桥长AB=( )m.
A. B.60 cos50° C. D.60 tan50°
【解答】由题意可得:∠ABC=90°,BC=60m,∠BCA=50°,
∴,
∴AB=BC tan50°=60 tan50°,
故选:D.
7.(3分)点A(3,y1)和点B(﹣2,y2)都在直线y=﹣2x+3上,则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
【解答】解:∵直线y=﹣2x+3中,k=﹣2<0,
∴此函数中y随x的增大而减小,
∵3>﹣2,
∴y1<y2.
故选:B.
8.(3分)如图,AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
【解答】解:设AF交BE于点G,
∵CD∥EF,
∴△GCD∽△GEF,
∴=,
故A不正确,D不正确;
∵CD∥EF,
∴=,
故B不正确;
∵CD∥EF,
∴=,
故C正确,
故选:C.
9.(3分)某商店购入一批衬衫进行销售,当每件盈利30元,每星期可以卖出100件,现需降价处理:每件衬衫售价每降价5元,每星期可以多卖出20个,店里每星期衬衫的利润要达到2800元.若设每件衬衫售价降低x元,则可列方程为( )
A.(30+x)(100﹣20x)=2800
B.(30+x)(100﹣4x)=2800
C.(30﹣x)(100+20x)=2800
D.(30﹣x)(100+4x)=2800
【解答】解:设每件衬衫售价降低x元,
根据题意得,(30﹣x)(100+4x)=2800,
故选:D.
10.(3分)周末小晨、小亮相约进行长跑比赛,两人同时起跑,刚跑出350米,小亮发现重要物品落在出发地,立刻原速返回,取回后以更快的速度投入比赛,若他们距离出发地y(m)与比赛时间x(min)的关系如图,下列说法正确的个数有( )
(1)小亮共跑了5200m;
(2)小晨全程的平均速度为250m/min;
(3)两人起跑以后第一次相遇时间为;
(4)小亮再次投入比赛后在距离终点750m时追上了小晨.
A.1个 B.2个 C.3个 D.4个
【解答】解:由图象可知,小亮共跑了350×2+4500=5200(m),故(1)正确;
∵4500÷18=250(m/min),
∴小晨全程的平均速度为250m/min,故(2)正确;
∵700÷2.5=280(m/min),
∴小亮最初速度为280m/min,
设两人起跑以后第一次相遇用x min,
则280x+250x=350×2,
解得x=,
∴两人起跑以后第一次相遇用min,故(3)错误;
小亮再次投入比赛的速度为=300(m/min),
设小亮再次投入比赛后在距离终点y m时追上了小晨,
则=﹣2.5,
解得y=750,
∴小亮再次投入比赛后在距离终点750m时追上了小晨.故(4)正确,
∴正确的有3个,
故选:C.
二、填空题(每小题3分,共计30分)
11.(3分)函数y=中,自变量x的取值范围是 x≠2 .
【解答】解:由题意得:x﹣2≠0,
解得:x≠2,
故答案为:x≠2.
12.(3分)函数y=kx+2的图象经过点(1,3),则k= 1 .
【解答】解:∵函数y=kx+2的图象经过点(1,3),
∴3=k×1+2,
解得k=1.
故答案为:1.
13.(3分)如图,图中所有四边形都是正方形,所有三角形都是直角三角形,其中最大的正方形的边长为5cm,则正方形A、B、C、D的面积和是 25 cm2.
【解答】解:由图形可知四个小正方形的面积和等于最大正方形的面积,
故正方形A,B,C,D的面积之和=52=25cm2.
故答案为:25.
14.(3分)关于x的一元二次方程:(a﹣1)x2+2x+a2﹣1=0的一个解是0,则a的值为 ﹣1 .
【解答】解:∵一元二次方程:(a﹣1)x2+2x+a2﹣1=0的一个解是0,
∴a﹣1≠0,a2﹣1=0,
解得a=﹣1,
故答案为:﹣1.
15.(3分)若平行四边形中两个内角的度数比为2:3,则其中较小的内角是 72 °.
【解答】解:设∠A=3x,∠B=2x,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴2x+3x=180°,
解得:x=36°,
∴∠B=2×36°=72°,
故答案为:72.
16.(3分)如图,在平行四边形ADBC中,点E是边AD的中点,EC交对角线AB于点F,则的值为 2 .
【解答】解:∵四边形ADBC是平行四边形,
∴BC∥AD,BC=AD,
∵点E是边AD的中点,
∴AD=2AE,
∴BC=2AE,
∵BC∥AE,
∴△BCF∽△AEF,
∴==2,
故答案为:2.
17.(3分)某种茶叶的价格两次下降,每次下降的百分率相同,原来每袋125元,现在每袋80元,则每次下降的百分率是 20% .
【解答】解:设每次下降的百分率为x,
根据题意得:125(1﹣x)2=80,
解得x=20%或x=(舍去),
∴每次下降的百分率是20%;
故答案为:20%.
18.(3分)如图,正方形ABCD,∠EAF=45°,∠EAF的两边分别交边BC,DC于点E、F,若BE=2,DF=3,则AF的长为 3 .
【解答】解:如图,延长CB到点G,使BG=DF,连接AG,
正方形ABCD中,AB=AD,∠D=∠DAB=∠ABC=90°,
∴∠ABG=90°=∠D,
又AB=AD,BG=DF,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,AG=AF,
∵∠EAF=45°,
∴∠DAF+∠BAE=∠BAG+∠BAE=∠EAG=90°﹣45°=45°,
∴∠EAG=∠EAF,
又AG=AF,AE=AE,
∴△GAE≌△FAE(SAS),
∴GE=FE,
∵GE=BG+BE=DF+BE,
∴FE=DF+BE=2+3=5,
设正方形ABCD的边长为a,
∴CE=BC﹣CE=a﹣2,CF=CD﹣DF=a﹣3,
∵FE2=CE2+CF2,
∴52=(a﹣2)2+(a﹣3)2,
∴a=﹣1(舍去)或a=6,
∴AF===3,
故答案为:3.
19.(3分)已知△ABC中,D、E分别是AB、AC的中点,F为直线BC上一点,EF=BC,∠EFC=50°,则∠EDF= 65或25 度.
【解答】解:如图1,∵D、E分别是AB、AC的中点,
∴DE=BC,DE∥BC,
∵EF=BC,∠EFC=50°,
∴ED=EF,∠DEF=∠EFC=50°,
∴∠EDF=65°,
如图2,∠DEF+∠EFC=180°,
∴∠DEF=130°,
∴∠EDF=25°,
故答案为:65或25.
20.(3分)如图,在Rt△ACB中,∠C=90°,点D为BC上一点,过点B作AD的垂线交AD的延长线于点E,若∠ABD+∠CDA=90°,4AD=5DE,,则线段BD的长为 8 .
【解答】解:∵∠C=90°,
∴∠CAD+∠CDA=90°,
∵∠ABD+∠CDA=90°,
∴∠CAD=∠ABD,
∵∠ACD=∠ACB,
∴△ACD∽△BCA,
∴AC:BC=CD:CA,
∴AC2=CD BC,
∵AC=3,
∴CD (CD+BD)=,
∴CD2+CD BD=90,
∵∠C=∠E=90°,∠CDA=∠EDB,
∴△ACD∽△BED,
∴CD:DE=AD:BD,
∴CD BD=DE AD,
∵4AD=5DE,
∴令AD=5x,DE=4x,
∴CD BD=20x2,
∴CD2+20x2=90,
∵CD2=AD2﹣AC2,
∴CD2=(5x)2﹣,
∴CD2=25x2﹣90,
∴25x2﹣90+20x2=90,
∴x=2(舍去负值),
∴AD=5x=10,DE=4x=8,
∴CD==,
∵CD BD=DE AD,
∴BD=8×10,
∴BD=8.
故答案为:8.
三、解答题:(21、22题每题7分;23、24题每题8分;25、26、27题每题10分)
21.(7分)先化简,再求的值,其中a=4cos30°﹣2tan45°.
【解答】解:
=
=
=,
当a=4cos30°﹣2tan45°=4×﹣2×1=2﹣2时,
原式===.
22.(7分)△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在小正方形的顶点上,每个小正方形边长均为1.
(1)以原点O为位似中心,在第三象限画出△A1B1C1,使△A1B1C1与△ABC的相似比为1:2;
(2)作出△ABC关于y轴对称的△A2B2C2;连接A2B,B2B,并直接写出∠A2BB2的正切值.
【解答】解:(1)如图,△A1B1C1为所作;使△A1B1C1与△ABC的相似比为1:2;
(2)如图,△A2B2C2为所作,tan∠A2BB2==.
23.(8分)如图,四边形ABCD中,AD∥BC,∠A=90°,点E为AB的中点,连接DE、CE,∠DEC=90°.
(1)求证:BE2=AD BC;
(2)若,AD=2,求DC的长.
【解答】(1)证明:∵AD∥BC,∠A=90°,
∴∠EBC=180°﹣∠A=90°,
∴∠A=∠EBC,
∵∠DEC=90°,
∴∠ADE=∠BEC=90°﹣∠AED,
∴△ADE∽△BEC,
∴=,
∴AE BE=AD BC,
∵点E为AB的中点,
∴AE=BE,
∴BE2=AD BC.
(2)解:∵△ADE∽△BEC,
∴==,
∵tan∠DCE==,AD=2,
∴===,
∴AE=BE=2AD=2×2=4,
∴BC=2AE=2×4=8,
延长DE、CB交于点F,则∠EBF=∠A,
在△BFE和△ADE中,
,
∴△BFE≌△ADE(ASA),
∴BF=AD=2,FE=DE,
∴CE垂直平分DF,
∴DC=FC=BF+BC=2+8=10,
∴DC的长为10.
24.(8分)如图1,在矩形ABCD中,连接AC,作AC的垂直平分线分别交AD、BC于点F、E,EF与AC的交点为G,连接AE和CF.
(1)试判断四边形AECF的形状,并说明理由;
(2)如图2,过点E作AD的垂线,分别交AC、AD于点K、H,直接写出与△FCG相似但不全等的三角形.
【解答】解:(1)四边形AECF是菱形.
理由:∵四边形ABCD是平行四边形,EF垂直平分AC,
∴AG=CG,∠AGF=∠CGE,AD∥BC,
∴∠CAD=∠ACB,
在△AGF和△CGE中,
,
∴△AGF≌△CGE(ASA),
∴EG=GF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形;
(2)△KAH∽△FCG,△KEG∽△FCG.
理由:∵四边形AECF是菱形,
∴FA=FC,
∴∠KAH=∠FCG,
∵EF⊥AC,EH⊥AD,
∴∠AHK=∠CGF=∠EGK=90°,
∴△KAH∽△FCG,
∴∠AKH=∠CFG,
∵∠AKH=∠EKG,
∴∠CFG=∠EKG,
∵∠CGF=∠EGK,
∴△KEG∽△FCG.
25.(10分)2023年哈尔滨马拉松比赛召开期间,某体育用品商店迎合市场热度,计划购进A、B种两种品牌的跑步鞋,若购进4双A品牌跑步鞋和3双B品牌跑步鞋,需要3200元,若购进3双A品牌跑步鞋和2双B品牌跑步鞋,需要2300元.
(1)求该商店购进A、B两种品牌跑步鞋的单价分别是多少?
(2)若商店共购进两种跑步鞋60双,且A品牌跑鞋的数量不多于B品牌跑步鞋的,如果这两种跑步鞋每双均加价20%出售,当购进A品牌跑步鞋多少双时,商店获得的总利润W最大,总利润W最大是多少?
【解答】解:(1)设每个A品牌跑步鞋的单价m元、每个B品牌跑步鞋的单价n元,根据题意,得:,
解得:,
答:每个A品牌跑步鞋的单价为500元、每个B品牌跑步鞋的单价为400元;
(2)∵两种跑步鞋60双,且A品牌跑鞋的数量不多于B品牌跑步鞋的,
∴x≥(60﹣x),
解得:x≥36,
60﹣x≥0,
解得:x≤60,
∴36≤x≤60,
在W=500×20%x+400×20%(60﹣x)=20x+4800,
∵20>0,
∴y随x的增大而增大,
∴当x=60时,W取得最大值,最大值为20×60+4800=6000,
即最大利润为6000元.
∴应购进A品牌跑步鞋60个,销售利润最大,为6000元.
26.(10分)在△ABC中,AB=AC,点D在线段CB的延长线上,连接AD,过点B作BE⊥BC交线段AD于点E,2∠BED+∠BAC=120°.
(1)如图1,求∠CAD的度数;
(2)如图2,若,求的值;
(3)如图3,在(2)的条件下,连接EC,EC交线段AB于点F,若BD=3,求AF的长.
【解答】解:(1)过点A作AH⊥BC于H,
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH=∠BAC,
∵2∠BED+∠BAC=120°,
∴∠BED+∠BAC=60°,
∵BE⊥BC,AH⊥BC,
∴AH∥BE,
∴∠BED=∠DAH,
∴∠DAH+∠BAC=60°=∠DAH+∠CAH,
∴∠CAD=60°;
(2)如图2,过点A作AH⊥BC于H,
∵AB=AC,AH⊥BC,
∴BH=CH,
∵AH∥BE,
∴=,
∴==;
(3)如图3,过点A作AH⊥BC于H,交EC于N,作△ACD的外接圆⊙O,连接AO,CO,DO,过点O作OM⊥CD于M,OP⊥AH于P,
∵,BD=3,
∴BC=4,
∴BH=CH=2,
∵BE∥AH,
∴△DEB∽△DHA,△HNC∽△BEC,
∴,,
∴NH=BE,BE=AH,
设BE=3a,则AH=5a,NH=a,
∴AN=a,
∵BE∥AH,
∴=,
∴AF=AB,
∵∠DOC=2∠DAC=120°,OD=OC,
∴∠ODC=∠OCD=30°,
∵OM⊥BC,CD=DB+BC=7,
∴DM=MC=,DM=OM,DO=2OM,
∴OM=,DO=7,
∵AH⊥BC,OM⊥CD,OP⊥AH,
∴四边形OMHP是矩形,
∴OM=PH=,OP=MH=MC﹣HC=,
∴AN===,
∴AH=+=10,
∴AB===4,
∴AF=AB=.
27.(10分)在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,C,过点C作CD∥OA交AB于点D,连接OD.
(1)如图1,求∠ADO的度数;
(2)如图2,点P在射线AO上(点P不与点A重合),过点P作PQ⊥AB,垂足为点Q,若AP=m,DQ=n,求出n与m的函数关系式,并直接写出m的取值范围;
(3)如图3,在(2)的条件下,当DQ=3时,连接OQ,在射线QA上是否存在点K,连接OK,使△OQK为等腰三角形,若存在,求出AK的长.
【解答】解:(1)当x=0,y=4,则B(0,4),
当y=0,x=4,则A(4,0),
∵CD∥OA,
∴当y=,x=3,则D(3,),
∴OA2=16,OD2=32+()2=12,AD2=(3﹣4)2+()2=4,
∵AD2+OD2=OA2,
∴△AOD是直角三角形,
∴∠ADO=90°;
(2)当P在线段OA上时,0<m≤4,如图:
由题意知,AO=4,AD=2,∠AQP=90°=∠ADO,
∵∠APQ=∠OAD,
∴△APQ∽△AOD,
∴,即,
解得n=2﹣,
当P在点O左侧,如图:
同理,△APQ∽△AOD,
∴,即,
解得n=,
综上所述,n与m的关系式为n=;
(3)由题意知,AQ=5,
如图,由题意知△OQK为等腰三角形,分OQ=OK3,OQ=QK2,OK1=OK1三种情况求解;
①当OQ=OK3,则OD为△OQK3底边QK3的高,
∴DK3=DQ=3,
∴AK3=DK3﹣AD=1;
②当OQ=QK2,
由勾股定理得,OQ==,
∴QK2=,
∴AK2=AQ﹣AK2=5﹣;
③当OK1=OK1,设K1(m,﹣m+4),
如图,过点Q作QM⊥OA与M,设OM=a,则AM=4﹣a,
由勾股定理得,QM2=OQ2﹣OM2=AQ2﹣AM2,
即()2﹣a2=52﹣(4﹣a)2,解得a=,
当a=,y=﹣×+4=,则Q(,),
∴m2+(m+4)2=(m﹣)2+(m+4﹣)2,
解得m=,
∴K1(,),
∴AK1==;
综上所述,AK的长为1或5﹣或.
第1页(共1页)
一、选择题(每小题3分,共30分)
1.(3分)下列方程中,是一元二次方程的是( )
A. B.x2﹣4=4
C.5x2+3x﹣2y=0 D.x﹣5=0
2.(3分)下列三角形中,不是直角三角形的是( )
A.三条边长之比为
B.三条边长之比为
C.三条边长之比为5:12:13
D.三个角度数之比为1:3:4
3.(3分)在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( )
A. B.2 C. D.
4.(3分)能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
5.(3分)如图,身高1.6m的小亮站在某路灯下,发现自己的影长恰好是3m,经测量,此时小亮离路灯底部的距离是9m,则路灯离地面的高度AB是( )
A.4.8m B.6m C.6.4m D.9m
6.(3分)如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50°,测得BC=60m,则桥长AB=( )m.
A. B.60 cos50° C. D.60 tan50°
7.(3分)点A(3,y1)和点B(﹣2,y2)都在直线y=﹣2x+3上,则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
8.(3分)如图,AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
9.(3分)某商店购入一批衬衫进行销售,当每件盈利30元,每星期可以卖出100件,现需降价处理:每件衬衫售价每降价5元,每星期可以多卖出20个,店里每星期衬衫的利润要达到2800元.若设每件衬衫售价降低x元,则可列方程为( )
A.(30+x)(100﹣20x)=2800
B.(30+x)(100﹣4x)=2800
C.(30﹣x)(100+20x)=2800
D.(30﹣x)(100+4x)=2800
10.(3分)周末小晨、小亮相约进行长跑比赛,两人同时起跑,刚跑出350米,小亮发现重要物品落在出发地,立刻原速返回,取回后以更快的速度投入比赛,若他们距离出发地y(m)与比赛时间x(min)的关系如图,下列说法正确的个数有( )
(1)小亮共跑了5200m;
(2)小晨全程的平均速度为250m/min;
(3)两人起跑以后第一次相遇时间为;
(4)小亮再次投入比赛后在距离终点750m时追上了小晨.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计30分)
11.(3分)函数y=中,自变量x的取值范围是 .
12.(3分)函数y=kx+2的图象经过点(1,3),则k= .
13.(3分)如图,图中所有四边形都是正方形,所有三角形都是直角三角形,其中最大的正方形的边长为5cm,则正方形A、B、C、D的面积和是 cm2.
14.(3分)关于x的一元二次方程:(a﹣1)x2+2x+a2﹣1=0的一个解是0,则a的值为 .
15.(3分)若平行四边形中两个内角的度数比为2:3,则其中较小的内角是 °.
16.(3分)如图,在平行四边形ADBC中,点E是边AD的中点,EC交对角线AB于点F,则的值为 .
17.(3分)某种茶叶的价格两次下降,每次下降的百分率相同,原来每袋125元,现在每袋80元,则每次下降的百分率是 .
18.(3分)如图,正方形ABCD,∠EAF=45°,∠EAF的两边分别交边BC,DC于点E、F,若BE=2,DF=3,则AF的长为 .
19.(3分)已知△ABC中,D、E分别是AB、AC的中点,F为直线BC上一点,EF=BC,∠EFC=50°,则∠EDF= 度.
20.(3分)如图,在Rt△ACB中,∠C=90°,点D为BC上一点,过点B作AD的垂线交AD的延长线于点E,若∠ABD+∠CDA=90°,4AD=5DE,,则线段BD的长为 .
三、解答题:(21、22题每题7分;23、24题每题8分;25、26、27题每题10分)
21.(7分)先化简,再求的值,其中a=4cos30°﹣2tan45°.
22.(7分)△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在小正方形的顶点上,每个小正方形边长均为1.
(1)以原点O为位似中心,在第三象限画出△A1B1C1,使△A1B1C1与△ABC的相似比为1:2;
(2)作出△ABC关于y轴对称的△A2B2C2;连接A2B,B2B,并直接写出∠A2BB2的正切值.
23.(8分)如图,四边形ABCD中,AD∥BC,∠A=90°,点E为AB的中点,连接DE、CE,∠DEC=90°.
(1)求证:BE2=AD BC;
(2)若,AD=2,求DC的长.
24.(8分)如图1,在矩形ABCD中,连接AC,作AC的垂直平分线分别交AD、BC于点F、E,EF与AC的交点为G,连接AE和CF.
(1)试判断四边形AECF的形状,并说明理由;
(2)如图2,过点E作AD的垂线,分别交AC、AD于点K、H,直接写出与△FCG相似但不全等的三角形.
25.(10分)2023年哈尔滨马拉松比赛召开期间,某体育用品商店迎合市场热度,计划购进A、B种两种品牌的跑步鞋,若购进4双A品牌跑步鞋和3双B品牌跑步鞋,需要3200元,若购进3双A品牌跑步鞋和2双B品牌跑步鞋,需要2300元.
(1)求该商店购进A、B两种品牌跑步鞋的单价分别是多少?
(2)若商店共购进两种跑步鞋60双,且A品牌跑鞋的数量不多于B品牌跑步鞋的,如果这两种跑步鞋每双均加价20%出售,当购进A品牌跑步鞋多少双时,商店获得的总利润W最大,总利润W最大是多少?
26.(10分)在△ABC中,AB=AC,点D在线段CB的延长线上,连接AD,过点B作BE⊥BC交线段AD于点E,2∠BED+∠BAC=120°.
(1)如图1,求∠CAD的度数;
(2)如图2,若,求的值;
(3)如图3,在(2)的条件下,连接EC,EC交线段AB于点F,若BD=3,求AF的长.
27.(10分)在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,C,过点C作CD∥OA交AB于点D,连接OD.
(1)如图1,求∠ADO的度数;
(2)如图2,点P在射线AO上(点P不与点A重合),过点P作PQ⊥AB,垂足为点Q,若AP=m,DQ=n,求出n与m的函数关系式,并直接写出m的取值范围;
(3)如图3,在(2)的条件下,当DQ=3时,连接OQ,在射线QA上是否存在点K,连接OK,使△OQK为等腰三角形,若存在,求出AK的长.
2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列方程中,是一元二次方程的是( )
A. B.x2﹣4=4
C.5x2+3x﹣2y=0 D.x﹣5=0
【解答】解:A、是分式方程,不符合题意;
B、x2﹣4=4是一元二次方程,符合题意;
C、5x2+3x﹣2y=0是二元二次方程,不符合题意;
D、x﹣5=0是一元一次方程,不符合题意.
故选:B.
2.(3分)下列三角形中,不是直角三角形的是( )
A.三条边长之比为
B.三条边长之比为
C.三条边长之比为5:12:13
D.三个角度数之比为1:3:4
【解答】解:A、()2+()2≠()2,不能作为直角三角形的三边长,故本选项符合题意;
B、12+22=()2,能作为直角三角形的三边长,故本选项不符合题意;
C、52+122=132,能作为直角三角形的三边长,故本选项符不合题意;
D、180°×=90°,是直角三角形,故此选项不合题意;
故选:A.
3.(3分)在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( )
A. B.2 C. D.
【解答】解:根据题意,AB==BC,sinA===.
故选:C.
4.(3分)能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
【解答】解:根据平行四边形的判定定理知,A、B、D均不符合是平行四边形的条件;
C满足两组对边分别相等的四边形是平行四边形.
故选:C.
5.(3分)如图,身高1.6m的小亮站在某路灯下,发现自己的影长恰好是3m,经测量,此时小亮离路灯底部的距离是9m,则路灯离地面的高度AB是( )
A.4.8m B.6m C.6.4m D.9m
【解答】解:如图,AD=9m,DE=3m,CD=1.8m,
∵CD∥AB,
∴△EDC∽△EAB,
∴=,即,
∴AB=6.4m.
故选:C.
6.(3分)如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=50°,测得BC=60m,则桥长AB=( )m.
A. B.60 cos50° C. D.60 tan50°
【解答】由题意可得:∠ABC=90°,BC=60m,∠BCA=50°,
∴,
∴AB=BC tan50°=60 tan50°,
故选:D.
7.(3分)点A(3,y1)和点B(﹣2,y2)都在直线y=﹣2x+3上,则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
【解答】解:∵直线y=﹣2x+3中,k=﹣2<0,
∴此函数中y随x的增大而减小,
∵3>﹣2,
∴y1<y2.
故选:B.
8.(3分)如图,AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
【解答】解:设AF交BE于点G,
∵CD∥EF,
∴△GCD∽△GEF,
∴=,
故A不正确,D不正确;
∵CD∥EF,
∴=,
故B不正确;
∵CD∥EF,
∴=,
故C正确,
故选:C.
9.(3分)某商店购入一批衬衫进行销售,当每件盈利30元,每星期可以卖出100件,现需降价处理:每件衬衫售价每降价5元,每星期可以多卖出20个,店里每星期衬衫的利润要达到2800元.若设每件衬衫售价降低x元,则可列方程为( )
A.(30+x)(100﹣20x)=2800
B.(30+x)(100﹣4x)=2800
C.(30﹣x)(100+20x)=2800
D.(30﹣x)(100+4x)=2800
【解答】解:设每件衬衫售价降低x元,
根据题意得,(30﹣x)(100+4x)=2800,
故选:D.
10.(3分)周末小晨、小亮相约进行长跑比赛,两人同时起跑,刚跑出350米,小亮发现重要物品落在出发地,立刻原速返回,取回后以更快的速度投入比赛,若他们距离出发地y(m)与比赛时间x(min)的关系如图,下列说法正确的个数有( )
(1)小亮共跑了5200m;
(2)小晨全程的平均速度为250m/min;
(3)两人起跑以后第一次相遇时间为;
(4)小亮再次投入比赛后在距离终点750m时追上了小晨.
A.1个 B.2个 C.3个 D.4个
【解答】解:由图象可知,小亮共跑了350×2+4500=5200(m),故(1)正确;
∵4500÷18=250(m/min),
∴小晨全程的平均速度为250m/min,故(2)正确;
∵700÷2.5=280(m/min),
∴小亮最初速度为280m/min,
设两人起跑以后第一次相遇用x min,
则280x+250x=350×2,
解得x=,
∴两人起跑以后第一次相遇用min,故(3)错误;
小亮再次投入比赛的速度为=300(m/min),
设小亮再次投入比赛后在距离终点y m时追上了小晨,
则=﹣2.5,
解得y=750,
∴小亮再次投入比赛后在距离终点750m时追上了小晨.故(4)正确,
∴正确的有3个,
故选:C.
二、填空题(每小题3分,共计30分)
11.(3分)函数y=中,自变量x的取值范围是 x≠2 .
【解答】解:由题意得:x﹣2≠0,
解得:x≠2,
故答案为:x≠2.
12.(3分)函数y=kx+2的图象经过点(1,3),则k= 1 .
【解答】解:∵函数y=kx+2的图象经过点(1,3),
∴3=k×1+2,
解得k=1.
故答案为:1.
13.(3分)如图,图中所有四边形都是正方形,所有三角形都是直角三角形,其中最大的正方形的边长为5cm,则正方形A、B、C、D的面积和是 25 cm2.
【解答】解:由图形可知四个小正方形的面积和等于最大正方形的面积,
故正方形A,B,C,D的面积之和=52=25cm2.
故答案为:25.
14.(3分)关于x的一元二次方程:(a﹣1)x2+2x+a2﹣1=0的一个解是0,则a的值为 ﹣1 .
【解答】解:∵一元二次方程:(a﹣1)x2+2x+a2﹣1=0的一个解是0,
∴a﹣1≠0,a2﹣1=0,
解得a=﹣1,
故答案为:﹣1.
15.(3分)若平行四边形中两个内角的度数比为2:3,则其中较小的内角是 72 °.
【解答】解:设∠A=3x,∠B=2x,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴2x+3x=180°,
解得:x=36°,
∴∠B=2×36°=72°,
故答案为:72.
16.(3分)如图,在平行四边形ADBC中,点E是边AD的中点,EC交对角线AB于点F,则的值为 2 .
【解答】解:∵四边形ADBC是平行四边形,
∴BC∥AD,BC=AD,
∵点E是边AD的中点,
∴AD=2AE,
∴BC=2AE,
∵BC∥AE,
∴△BCF∽△AEF,
∴==2,
故答案为:2.
17.(3分)某种茶叶的价格两次下降,每次下降的百分率相同,原来每袋125元,现在每袋80元,则每次下降的百分率是 20% .
【解答】解:设每次下降的百分率为x,
根据题意得:125(1﹣x)2=80,
解得x=20%或x=(舍去),
∴每次下降的百分率是20%;
故答案为:20%.
18.(3分)如图,正方形ABCD,∠EAF=45°,∠EAF的两边分别交边BC,DC于点E、F,若BE=2,DF=3,则AF的长为 3 .
【解答】解:如图,延长CB到点G,使BG=DF,连接AG,
正方形ABCD中,AB=AD,∠D=∠DAB=∠ABC=90°,
∴∠ABG=90°=∠D,
又AB=AD,BG=DF,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,AG=AF,
∵∠EAF=45°,
∴∠DAF+∠BAE=∠BAG+∠BAE=∠EAG=90°﹣45°=45°,
∴∠EAG=∠EAF,
又AG=AF,AE=AE,
∴△GAE≌△FAE(SAS),
∴GE=FE,
∵GE=BG+BE=DF+BE,
∴FE=DF+BE=2+3=5,
设正方形ABCD的边长为a,
∴CE=BC﹣CE=a﹣2,CF=CD﹣DF=a﹣3,
∵FE2=CE2+CF2,
∴52=(a﹣2)2+(a﹣3)2,
∴a=﹣1(舍去)或a=6,
∴AF===3,
故答案为:3.
19.(3分)已知△ABC中,D、E分别是AB、AC的中点,F为直线BC上一点,EF=BC,∠EFC=50°,则∠EDF= 65或25 度.
【解答】解:如图1,∵D、E分别是AB、AC的中点,
∴DE=BC,DE∥BC,
∵EF=BC,∠EFC=50°,
∴ED=EF,∠DEF=∠EFC=50°,
∴∠EDF=65°,
如图2,∠DEF+∠EFC=180°,
∴∠DEF=130°,
∴∠EDF=25°,
故答案为:65或25.
20.(3分)如图,在Rt△ACB中,∠C=90°,点D为BC上一点,过点B作AD的垂线交AD的延长线于点E,若∠ABD+∠CDA=90°,4AD=5DE,,则线段BD的长为 8 .
【解答】解:∵∠C=90°,
∴∠CAD+∠CDA=90°,
∵∠ABD+∠CDA=90°,
∴∠CAD=∠ABD,
∵∠ACD=∠ACB,
∴△ACD∽△BCA,
∴AC:BC=CD:CA,
∴AC2=CD BC,
∵AC=3,
∴CD (CD+BD)=,
∴CD2+CD BD=90,
∵∠C=∠E=90°,∠CDA=∠EDB,
∴△ACD∽△BED,
∴CD:DE=AD:BD,
∴CD BD=DE AD,
∵4AD=5DE,
∴令AD=5x,DE=4x,
∴CD BD=20x2,
∴CD2+20x2=90,
∵CD2=AD2﹣AC2,
∴CD2=(5x)2﹣,
∴CD2=25x2﹣90,
∴25x2﹣90+20x2=90,
∴x=2(舍去负值),
∴AD=5x=10,DE=4x=8,
∴CD==,
∵CD BD=DE AD,
∴BD=8×10,
∴BD=8.
故答案为:8.
三、解答题:(21、22题每题7分;23、24题每题8分;25、26、27题每题10分)
21.(7分)先化简,再求的值,其中a=4cos30°﹣2tan45°.
【解答】解:
=
=
=,
当a=4cos30°﹣2tan45°=4×﹣2×1=2﹣2时,
原式===.
22.(7分)△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在小正方形的顶点上,每个小正方形边长均为1.
(1)以原点O为位似中心,在第三象限画出△A1B1C1,使△A1B1C1与△ABC的相似比为1:2;
(2)作出△ABC关于y轴对称的△A2B2C2;连接A2B,B2B,并直接写出∠A2BB2的正切值.
【解答】解:(1)如图,△A1B1C1为所作;使△A1B1C1与△ABC的相似比为1:2;
(2)如图,△A2B2C2为所作,tan∠A2BB2==.
23.(8分)如图,四边形ABCD中,AD∥BC,∠A=90°,点E为AB的中点,连接DE、CE,∠DEC=90°.
(1)求证:BE2=AD BC;
(2)若,AD=2,求DC的长.
【解答】(1)证明:∵AD∥BC,∠A=90°,
∴∠EBC=180°﹣∠A=90°,
∴∠A=∠EBC,
∵∠DEC=90°,
∴∠ADE=∠BEC=90°﹣∠AED,
∴△ADE∽△BEC,
∴=,
∴AE BE=AD BC,
∵点E为AB的中点,
∴AE=BE,
∴BE2=AD BC.
(2)解:∵△ADE∽△BEC,
∴==,
∵tan∠DCE==,AD=2,
∴===,
∴AE=BE=2AD=2×2=4,
∴BC=2AE=2×4=8,
延长DE、CB交于点F,则∠EBF=∠A,
在△BFE和△ADE中,
,
∴△BFE≌△ADE(ASA),
∴BF=AD=2,FE=DE,
∴CE垂直平分DF,
∴DC=FC=BF+BC=2+8=10,
∴DC的长为10.
24.(8分)如图1,在矩形ABCD中,连接AC,作AC的垂直平分线分别交AD、BC于点F、E,EF与AC的交点为G,连接AE和CF.
(1)试判断四边形AECF的形状,并说明理由;
(2)如图2,过点E作AD的垂线,分别交AC、AD于点K、H,直接写出与△FCG相似但不全等的三角形.
【解答】解:(1)四边形AECF是菱形.
理由:∵四边形ABCD是平行四边形,EF垂直平分AC,
∴AG=CG,∠AGF=∠CGE,AD∥BC,
∴∠CAD=∠ACB,
在△AGF和△CGE中,
,
∴△AGF≌△CGE(ASA),
∴EG=GF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形;
(2)△KAH∽△FCG,△KEG∽△FCG.
理由:∵四边形AECF是菱形,
∴FA=FC,
∴∠KAH=∠FCG,
∵EF⊥AC,EH⊥AD,
∴∠AHK=∠CGF=∠EGK=90°,
∴△KAH∽△FCG,
∴∠AKH=∠CFG,
∵∠AKH=∠EKG,
∴∠CFG=∠EKG,
∵∠CGF=∠EGK,
∴△KEG∽△FCG.
25.(10分)2023年哈尔滨马拉松比赛召开期间,某体育用品商店迎合市场热度,计划购进A、B种两种品牌的跑步鞋,若购进4双A品牌跑步鞋和3双B品牌跑步鞋,需要3200元,若购进3双A品牌跑步鞋和2双B品牌跑步鞋,需要2300元.
(1)求该商店购进A、B两种品牌跑步鞋的单价分别是多少?
(2)若商店共购进两种跑步鞋60双,且A品牌跑鞋的数量不多于B品牌跑步鞋的,如果这两种跑步鞋每双均加价20%出售,当购进A品牌跑步鞋多少双时,商店获得的总利润W最大,总利润W最大是多少?
【解答】解:(1)设每个A品牌跑步鞋的单价m元、每个B品牌跑步鞋的单价n元,根据题意,得:,
解得:,
答:每个A品牌跑步鞋的单价为500元、每个B品牌跑步鞋的单价为400元;
(2)∵两种跑步鞋60双,且A品牌跑鞋的数量不多于B品牌跑步鞋的,
∴x≥(60﹣x),
解得:x≥36,
60﹣x≥0,
解得:x≤60,
∴36≤x≤60,
在W=500×20%x+400×20%(60﹣x)=20x+4800,
∵20>0,
∴y随x的增大而增大,
∴当x=60时,W取得最大值,最大值为20×60+4800=6000,
即最大利润为6000元.
∴应购进A品牌跑步鞋60个,销售利润最大,为6000元.
26.(10分)在△ABC中,AB=AC,点D在线段CB的延长线上,连接AD,过点B作BE⊥BC交线段AD于点E,2∠BED+∠BAC=120°.
(1)如图1,求∠CAD的度数;
(2)如图2,若,求的值;
(3)如图3,在(2)的条件下,连接EC,EC交线段AB于点F,若BD=3,求AF的长.
【解答】解:(1)过点A作AH⊥BC于H,
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH=∠BAC,
∵2∠BED+∠BAC=120°,
∴∠BED+∠BAC=60°,
∵BE⊥BC,AH⊥BC,
∴AH∥BE,
∴∠BED=∠DAH,
∴∠DAH+∠BAC=60°=∠DAH+∠CAH,
∴∠CAD=60°;
(2)如图2,过点A作AH⊥BC于H,
∵AB=AC,AH⊥BC,
∴BH=CH,
∵AH∥BE,
∴=,
∴==;
(3)如图3,过点A作AH⊥BC于H,交EC于N,作△ACD的外接圆⊙O,连接AO,CO,DO,过点O作OM⊥CD于M,OP⊥AH于P,
∵,BD=3,
∴BC=4,
∴BH=CH=2,
∵BE∥AH,
∴△DEB∽△DHA,△HNC∽△BEC,
∴,,
∴NH=BE,BE=AH,
设BE=3a,则AH=5a,NH=a,
∴AN=a,
∵BE∥AH,
∴=,
∴AF=AB,
∵∠DOC=2∠DAC=120°,OD=OC,
∴∠ODC=∠OCD=30°,
∵OM⊥BC,CD=DB+BC=7,
∴DM=MC=,DM=OM,DO=2OM,
∴OM=,DO=7,
∵AH⊥BC,OM⊥CD,OP⊥AH,
∴四边形OMHP是矩形,
∴OM=PH=,OP=MH=MC﹣HC=,
∴AN===,
∴AH=+=10,
∴AB===4,
∴AF=AB=.
27.(10分)在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,C,过点C作CD∥OA交AB于点D,连接OD.
(1)如图1,求∠ADO的度数;
(2)如图2,点P在射线AO上(点P不与点A重合),过点P作PQ⊥AB,垂足为点Q,若AP=m,DQ=n,求出n与m的函数关系式,并直接写出m的取值范围;
(3)如图3,在(2)的条件下,当DQ=3时,连接OQ,在射线QA上是否存在点K,连接OK,使△OQK为等腰三角形,若存在,求出AK的长.
【解答】解:(1)当x=0,y=4,则B(0,4),
当y=0,x=4,则A(4,0),
∵CD∥OA,
∴当y=,x=3,则D(3,),
∴OA2=16,OD2=32+()2=12,AD2=(3﹣4)2+()2=4,
∵AD2+OD2=OA2,
∴△AOD是直角三角形,
∴∠ADO=90°;
(2)当P在线段OA上时,0<m≤4,如图:
由题意知,AO=4,AD=2,∠AQP=90°=∠ADO,
∵∠APQ=∠OAD,
∴△APQ∽△AOD,
∴,即,
解得n=2﹣,
当P在点O左侧,如图:
同理,△APQ∽△AOD,
∴,即,
解得n=,
综上所述,n与m的关系式为n=;
(3)由题意知,AQ=5,
如图,由题意知△OQK为等腰三角形,分OQ=OK3,OQ=QK2,OK1=OK1三种情况求解;
①当OQ=OK3,则OD为△OQK3底边QK3的高,
∴DK3=DQ=3,
∴AK3=DK3﹣AD=1;
②当OQ=QK2,
由勾股定理得,OQ==,
∴QK2=,
∴AK2=AQ﹣AK2=5﹣;
③当OK1=OK1,设K1(m,﹣m+4),
如图,过点Q作QM⊥OA与M,设OM=a,则AM=4﹣a,
由勾股定理得,QM2=OQ2﹣OM2=AQ2﹣AM2,
即()2﹣a2=52﹣(4﹣a)2,解得a=,
当a=,y=﹣×+4=,则Q(,),
∴m2+(m+4)2=(m﹣)2+(m+4﹣)2,
解得m=,
∴K1(,),
∴AK1==;
综上所述,AK的长为1或5﹣或.
第1页(共1页)
同课章节目录
