黑龙江省哈尔滨市南岗区2022-2023学年八年级(上)期末数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市南岗区2022-2023学年八年级(上)期末数学试卷(五四学制)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 468.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览




文档简介
2022-2023学年黑龙江省哈尔滨市南岗区八年级(上)期末数学试卷(五四学制)
一、选择题(每小题3分,共计24分)
1.(3分)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
2.(3分)计算a2 a的正确结果是( )
A.2a B.a2 C.a3 D.2a2
3.(3分)若在实数范围内有意义,则x的取值范围( )
A.x≥2 B.x≤2 C.x>2 D.x<2
4.(3分)代数式,,,中,属于分式的有( )
A.1个 B.2个 C.3个 D.4个
5.(3分)下列运算正确的是( )
A.(a2)3=a6 B.3a﹣2a=1
C.(ab2)2=ab4 D.a6÷a2=a3
6.(3分)化简的结果是( )
A.5 B.±5 C.﹣5 D.25
7.(3分)计算x2y﹣3(x﹣1y)3的正确结果是( )
A.x B. C. D.0
8.(3分)如图,等边三角形ABC中,AD是BC上的高,点E,F分别在AB,AC上,且∠BDE=∠CDF=60°,则图中与BD相等的线段(不包含BD)一共有( )
A.4条 B.6条 C.7条 D.8条
二、填空题(每小题3分,共计30分)
9.(3分)随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.00000000034m,用科学记数法表示是 .
10.(3分)当x= 时,分式的值为0.
11.(3分)计算的结果是 .
12.(3分)把多项式x2y﹣4y分解因式的结果是 .
13.(3分)已知≈1.414,则的近似值为 (结果保留小数点后两位).
14.(3分)分式方程=的解是 .
15.(3分)若等腰三角形的两边长分别是2cm和3cm,则这个等腰三角形的周长是 cm.
16.(3分)已知,,则x2+2xy+y2的值为 .
17.(3分)某次列车平均提速vkm/h,用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,可求得提速前列车的平均速度为 km/h.
18.(3分)如图,在△ABC中,AB=5,BC=3,以点B为圆心,BC长为半径画弧,与AC交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,交AB于点G,连接DG,则△BDG的周长为 .
三、解答题(其中19-21题各8分,22-24题各10分,25题12分,共计66分)
19.(8分)计算:
(1)(2a)3 b4÷12a3b2;
(2)(3x+1)(x+2).
20.(8分)计算:
(1)×
(2)2﹣6+3.
21.(8分)先化简,再求代数式的值,其中m为满足0<m<4的整数.
22.(10分)解方程与不等式:
(1)(x+2)(x﹣2)﹣(x﹣1)(x+5)=1;
(2)4(x+1)2﹣(2x+5)(2x﹣5)≤21.
23.(10分)如图,△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,﹣1),C(﹣3,2).
(1)已知△ABC和△A1B1C1关于x轴对称,点A1,B1,C1分别是点A,B,C的对称点,请直接写出点A1,B1,C1的坐标;
(2)在图中画出△ABC关于y轴对称的△A2B2C2.
24.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠550米,甲施工队施工5天后,增加施工人员,每天比原来多修建30米,再施工2天完成任务.甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建450米后,通过技术更新,每天比原来多修建25%,灌溉水渠完工时,两施工队修建的长度恰好相同.乙施工队原来每天修建灌溉水渠多少米?
25.(12分)已知:在△ABC中,∠ACB=90°,∠A=60°.点D在AB上,且AD=AC,连接CD.
(1)如图1,求证:BD=CD;
(2)过点D作△DEF,使∠DEF=90°,∠EDF=60°.连接CE并延长CE至点G,使EG=CE,连接BF,BG,FG.
①如图2,当点F在DB的延长线上时,求证:△BFG是等边三角形;
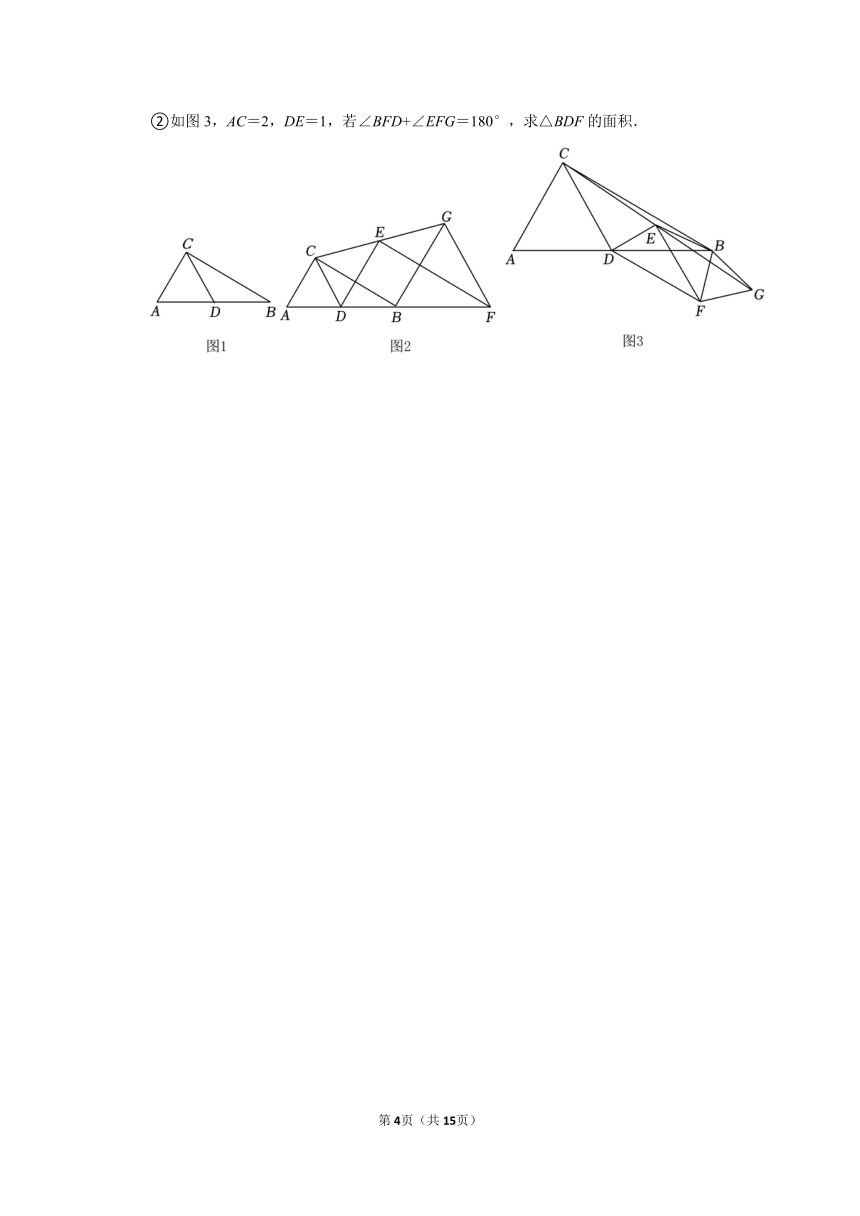
②如图3,AC=2,DE=1,若∠BFD+∠EFG=180°,求△BDF的面积.
2022-2023学年黑龙江省哈尔滨市南岗区八年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计24分)
1.(3分)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
2.(3分)计算a2 a的正确结果是( )
A.2a B.a2 C.a3 D.2a2
【解答】解:a2 a=a3.
故选:C.
3.(3分)若在实数范围内有意义,则x的取值范围( )
A.x≥2 B.x≤2 C.x>2 D.x<2
【解答】解:∵在实数范围内有意义,
∴x﹣2≥0,解得x≥2.
故选:A.
4.(3分)代数式,,,中,属于分式的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:,的分母中不含有字母,因此它们是整式,而不是分式;,的分母中含有字母,因此它们是分式,
故选:B.
5.(3分)下列运算正确的是( )
A.(a2)3=a6 B.3a﹣2a=1
C.(ab2)2=ab4 D.a6÷a2=a3
【解答】解:A、(a2)3=a6,故A符合题意;
B、3a﹣2a=a,故B不符合题意;
C、(ab2)2=a2b4,故C不符合题意;
D、a6÷a2=a4,故D不符合题意;
故选:A.
6.(3分)化简的结果是( )
A.5 B.±5 C.﹣5 D.25
【解答】解:原式==5;
故选:A.
7.(3分)计算x2y﹣3(x﹣1y)3的正确结果是( )
A.x B. C. D.0
【解答】解:x2y﹣3(x﹣1y)3
=x2y﹣3(x﹣3y3)
=x﹣1
=.
故选:B.
8.(3分)如图,等边三角形ABC中,AD是BC上的高,点E,F分别在AB,AC上,且∠BDE=∠CDF=60°,则图中与BD相等的线段(不包含BD)一共有( )
A.4条 B.6条 C.7条 D.8条
【解答】解:如图,连接EF.
∵等边△ABC中,AD是BC边上的高,
∴∠BAD=∠CAD=30°,
∵∠BDE=∠CDF=60°,
∴∠ADE=∠ADF=30°,
∴∠EDF=60°,
△AEF、△BDE、△CDF、△DEF都是全等的等边三角形,
∴BD=DC=DE=BE=AE=AF=FC=FD,
即图中与BD相等的线段有7条.
故选:C.
二、填空题(每小题3分,共计30分)
9.(3分)随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.00000000034m,用科学记数法表示是 3.4×10﹣10 .
【解答】解:0.00000000034=3.4×10﹣10,
故答案为:3.4×10﹣10
10.(3分)当x= 1 时,分式的值为0.
【解答】解:由题意得:x﹣1=0,且x≠0,
∴x=1,
∴当x=1时,的值为0.
故答案为:1.
11.(3分)计算的结果是 x .
【解答】解:原式=
=.
故答案为:x.
12.(3分)把多项式x2y﹣4y分解因式的结果是 y(x+2)(x﹣2) .
【解答】解:x2y﹣4y
=y(x2﹣4)
=y(x+2)(x﹣2).
故答案为:y(x+2)(x﹣2).
13.(3分)已知≈1.414,则的近似值为 2.83 (结果保留小数点后两位).
【解答】解:=2≈2.83,
故答案为:2.83.
14.(3分)分式方程=的解是 x=5 .
【解答】解:去分母得:2x﹣2=x+3,
解得:x=5,
经检验x=5是分式方程的解.
故答案为:x=5
15.(3分)若等腰三角形的两边长分别是2cm和3cm,则这个等腰三角形的周长是 8或7 cm.
【解答】解:当2cm为底时,则其它两边都为3cm,
3cm、3cm、2cm可以构成三角形,
所以周长为8cm;
当3cm为底时,
其它两边为2cm和2cm,能构成三角形,
所以周长为7cm.
故答案为:8或7.
16.(3分)已知,,则x2+2xy+y2的值为 12 .
【解答】解:∵,,
∴x2+2xy+y2=(x+y)2=(+1+﹣1)2=(2)2=12;
故答案为:12.
17.(3分)某次列车平均提速vkm/h,用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,可求得提速前列车的平均速度为 km/h.
【解答】解:设提速前列车的平均速度为xkm/h,根据题意可得:
=,
解得:x=.
故答案为:.
18.(3分)如图,在△ABC中,AB=5,BC=3,以点B为圆心,BC长为半径画弧,与AC交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,交AB于点G,连接DG,则△BDG的周长为 8 .
【解答】解:由题意知,BD=BC,直线EF为线段AD的垂直平分线,
∴AG=DG,
∴△BDG的周长为BD+DG+BG=BC+AG+BG=BC+AB=8.
故答案为:8.
三、解答题(其中19-21题各8分,22-24题各10分,25题12分,共计66分)
19.(8分)计算:
(1)(2a)3 b4÷12a3b2;
(2)(3x+1)(x+2).
【解答】解:(1)原式=8a3 b4÷12a3b2=;
(2)原式=3x2+6x+x+2=3x2+7x+2.
20.(8分)计算:
(1)×
(2)2﹣6+3.
【解答】解:(1)原式=3×5÷
=15÷
=15;
(2)原式=4﹣2+12
=14.
21.(8分)先化简,再求代数式的值,其中m为满足0<m<4的整数.
【解答】解:原式=
=
=m+3,
∵m﹣2≠0,m﹣3≠0,
∴m≠2,m≠3,
又∵m为满足0<m<4的整数,
∴m=1,
∴原式=1+3=4.
22.(10分)解方程与不等式:
(1)(x+2)(x﹣2)﹣(x﹣1)(x+5)=1;
(2)4(x+1)2﹣(2x+5)(2x﹣5)≤21.
【解答】解:x2﹣4﹣(x2+5x﹣x﹣5)=1,
x2﹣4﹣x2﹣5x+x+5=1,
﹣4x=0,
x=0;
(2)4(x2+2x+1)﹣(4x2﹣25)≤21,
4x2+8x+4﹣4x2+25≤21,
8x≤﹣8,
x≤﹣1.
23.(10分)如图,△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,﹣1),C(﹣3,2).
(1)已知△ABC和△A1B1C1关于x轴对称,点A1,B1,C1分别是点A,B,C的对称点,请直接写出点A1,B1,C1的坐标;
(2)在图中画出△ABC关于y轴对称的△A2B2C2.
【解答】解:(1)∵A(﹣4,1),B(﹣1,﹣1),C(﹣3,2),
∴A1(﹣4,﹣1),B1(﹣1,1),C1(﹣3,﹣2).
(2)如图,△A2B2C2即为所求.
24.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠550米,甲施工队施工5天后,增加施工人员,每天比原来多修建30米,再施工2天完成任务.甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建450米后,通过技术更新,每天比原来多修建25%,灌溉水渠完工时,两施工队修建的长度恰好相同.乙施工队原来每天修建灌溉水渠多少米?
【解答】解:(1)设甲施工队增加人员后每天修建灌溉水渠x米,则原计划每天施工(x﹣30)米,
由题意可得:5(x﹣30)+2x=550,
解得x=100,
答:甲施工队增加人员后每天修建灌溉水渠100米;
(2)设乙施工队原来每天修建灌溉水渠m米,则技术更新后每天修建水渠m(1+25%)=1.2m米,
由题意可得:+=,
解得m=90,
经检验,m=90是原分式方程的解,
答:乙施工队原来每天修建灌溉水渠90米.
25.(12分)已知:在△ABC中,∠ACB=90°,∠A=60°.点D在AB上,且AD=AC,连接CD.
(1)如图1,求证:BD=CD;
(2)过点D作△DEF,使∠DEF=90°,∠EDF=60°.连接CE并延长CE至点G,使EG=CE,连接BF,BG,FG.
①如图2,当点F在DB的延长线上时,求证:△BFG是等边三角形;
②如图3,AC=2,DE=1,若∠BFD+∠EFG=180°,求△BDF的面积.
【解答】(1)证明:∵DA=CA,∠A=60°,
∴△ACD是等边三角形,
∴AC=CD,∠ACD=∠A=60°,
∵∠ACB=90°,
∴∠ABC=90°﹣∠A=90°﹣∠ACD=90°﹣60°=30°,
∴∠ABC=∠BCD,
∴BD=CD;
(2)①证明:如图2,延长FE,DC交于点K,
∵∠FED=90°,
∴∠EFD=90°﹣∠FDE=30°,
∴∠K=∠KDA﹣∠DFK=60°﹣30°=30°,
∴∠K=∠DFK,
∴FD=KD,
又∵DB=DC,
∴CK=BF,
∵∠DEF=90°,
∴DE⊥FK
又∵DK=DF,
∴EK=EF,
又∵∠CEK=∠GEF,CE=EG,
∴△CEK≌△GEF(SAS),
∴FG=CK,∠GFK=∠K=30°,
∴FG=BF,∠GFB=∠GFK+∠DFK=30°+30°=60°,
∴△BFG是等边三角形;
②解:如图3延长DE至H,使EH=DE,连接FH,GH,过点B作BM⊥DF于点M,
∵CE=EG,∠CED=∠GEH,DE=EH,
∴△CDE≌△GHE(SAS),
∴GH=CD,∠CDE=∠GHE,
∵BD=CD,
∴GH=BD,
∵∠DEF=90°,
∴FE⊥DH,
又∵DE=EH,
∴FH=FD
又∵∠FDH=60°,
∴△DFH是等边三角形
∴∠DFH=∠DHF=60°,
∴∠EFH=90°﹣∠DHF=90°﹣60°=30°,
设∠FHC=α,
∴∠CDE=∠GHE=α+60°,
∴∠BDE=∠BDC﹣∠CDF=120°﹣(α+60°)=60°﹣α,
∴∠BDF=∠FDF﹣∠BDF=60°﹣(60°﹣α)=α,
∴∠BDF=∠FHG,
∴△BDF≌△GHF(SAS),
∴∠BFD=∠GFH,
令∠BFD=β,则∠GFH=β,
∴∠FFG=∠GFH+∠FFH=β+30°,
∵∠BFD+∠FFG=180°,
∴β+β+30°=180°,
∴β=75°,
∴∠BFD=75°,
在Rt△DEF中,∠DFE=30°,
∴DF=2DE=2,
又∵BD=CD=AD=2,
∴BD=DF,
∴∠DBF=∠BFD=75°,
∴∠BDF=180°﹣75°﹣75°=30°,
在Rt△BDM中,,
∴.
第1页(共1页)
一、选择题(每小题3分,共计24分)
1.(3分)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
2.(3分)计算a2 a的正确结果是( )
A.2a B.a2 C.a3 D.2a2
3.(3分)若在实数范围内有意义,则x的取值范围( )
A.x≥2 B.x≤2 C.x>2 D.x<2
4.(3分)代数式,,,中,属于分式的有( )
A.1个 B.2个 C.3个 D.4个
5.(3分)下列运算正确的是( )
A.(a2)3=a6 B.3a﹣2a=1
C.(ab2)2=ab4 D.a6÷a2=a3
6.(3分)化简的结果是( )
A.5 B.±5 C.﹣5 D.25
7.(3分)计算x2y﹣3(x﹣1y)3的正确结果是( )
A.x B. C. D.0
8.(3分)如图,等边三角形ABC中,AD是BC上的高,点E,F分别在AB,AC上,且∠BDE=∠CDF=60°,则图中与BD相等的线段(不包含BD)一共有( )
A.4条 B.6条 C.7条 D.8条
二、填空题(每小题3分,共计30分)
9.(3分)随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.00000000034m,用科学记数法表示是 .
10.(3分)当x= 时,分式的值为0.
11.(3分)计算的结果是 .
12.(3分)把多项式x2y﹣4y分解因式的结果是 .
13.(3分)已知≈1.414,则的近似值为 (结果保留小数点后两位).
14.(3分)分式方程=的解是 .
15.(3分)若等腰三角形的两边长分别是2cm和3cm,则这个等腰三角形的周长是 cm.
16.(3分)已知,,则x2+2xy+y2的值为 .
17.(3分)某次列车平均提速vkm/h,用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,可求得提速前列车的平均速度为 km/h.
18.(3分)如图,在△ABC中,AB=5,BC=3,以点B为圆心,BC长为半径画弧,与AC交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,交AB于点G,连接DG,则△BDG的周长为 .
三、解答题(其中19-21题各8分,22-24题各10分,25题12分,共计66分)
19.(8分)计算:
(1)(2a)3 b4÷12a3b2;
(2)(3x+1)(x+2).
20.(8分)计算:
(1)×
(2)2﹣6+3.
21.(8分)先化简,再求代数式的值,其中m为满足0<m<4的整数.
22.(10分)解方程与不等式:
(1)(x+2)(x﹣2)﹣(x﹣1)(x+5)=1;
(2)4(x+1)2﹣(2x+5)(2x﹣5)≤21.
23.(10分)如图,△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,﹣1),C(﹣3,2).
(1)已知△ABC和△A1B1C1关于x轴对称,点A1,B1,C1分别是点A,B,C的对称点,请直接写出点A1,B1,C1的坐标;
(2)在图中画出△ABC关于y轴对称的△A2B2C2.
24.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠550米,甲施工队施工5天后,增加施工人员,每天比原来多修建30米,再施工2天完成任务.甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建450米后,通过技术更新,每天比原来多修建25%,灌溉水渠完工时,两施工队修建的长度恰好相同.乙施工队原来每天修建灌溉水渠多少米?
25.(12分)已知:在△ABC中,∠ACB=90°,∠A=60°.点D在AB上,且AD=AC,连接CD.
(1)如图1,求证:BD=CD;
(2)过点D作△DEF,使∠DEF=90°,∠EDF=60°.连接CE并延长CE至点G,使EG=CE,连接BF,BG,FG.
①如图2,当点F在DB的延长线上时,求证:△BFG是等边三角形;
②如图3,AC=2,DE=1,若∠BFD+∠EFG=180°,求△BDF的面积.
2022-2023学年黑龙江省哈尔滨市南岗区八年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计24分)
1.(3分)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
2.(3分)计算a2 a的正确结果是( )
A.2a B.a2 C.a3 D.2a2
【解答】解:a2 a=a3.
故选:C.
3.(3分)若在实数范围内有意义,则x的取值范围( )
A.x≥2 B.x≤2 C.x>2 D.x<2
【解答】解:∵在实数范围内有意义,
∴x﹣2≥0,解得x≥2.
故选:A.
4.(3分)代数式,,,中,属于分式的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:,的分母中不含有字母,因此它们是整式,而不是分式;,的分母中含有字母,因此它们是分式,
故选:B.
5.(3分)下列运算正确的是( )
A.(a2)3=a6 B.3a﹣2a=1
C.(ab2)2=ab4 D.a6÷a2=a3
【解答】解:A、(a2)3=a6,故A符合题意;
B、3a﹣2a=a,故B不符合题意;
C、(ab2)2=a2b4,故C不符合题意;
D、a6÷a2=a4,故D不符合题意;
故选:A.
6.(3分)化简的结果是( )
A.5 B.±5 C.﹣5 D.25
【解答】解:原式==5;
故选:A.
7.(3分)计算x2y﹣3(x﹣1y)3的正确结果是( )
A.x B. C. D.0
【解答】解:x2y﹣3(x﹣1y)3
=x2y﹣3(x﹣3y3)
=x﹣1
=.
故选:B.
8.(3分)如图,等边三角形ABC中,AD是BC上的高,点E,F分别在AB,AC上,且∠BDE=∠CDF=60°,则图中与BD相等的线段(不包含BD)一共有( )
A.4条 B.6条 C.7条 D.8条
【解答】解:如图,连接EF.
∵等边△ABC中,AD是BC边上的高,
∴∠BAD=∠CAD=30°,
∵∠BDE=∠CDF=60°,
∴∠ADE=∠ADF=30°,
∴∠EDF=60°,
△AEF、△BDE、△CDF、△DEF都是全等的等边三角形,
∴BD=DC=DE=BE=AE=AF=FC=FD,
即图中与BD相等的线段有7条.
故选:C.
二、填空题(每小题3分,共计30分)
9.(3分)随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.00000000034m,用科学记数法表示是 3.4×10﹣10 .
【解答】解:0.00000000034=3.4×10﹣10,
故答案为:3.4×10﹣10
10.(3分)当x= 1 时,分式的值为0.
【解答】解:由题意得:x﹣1=0,且x≠0,
∴x=1,
∴当x=1时,的值为0.
故答案为:1.
11.(3分)计算的结果是 x .
【解答】解:原式=
=.
故答案为:x.
12.(3分)把多项式x2y﹣4y分解因式的结果是 y(x+2)(x﹣2) .
【解答】解:x2y﹣4y
=y(x2﹣4)
=y(x+2)(x﹣2).
故答案为:y(x+2)(x﹣2).
13.(3分)已知≈1.414,则的近似值为 2.83 (结果保留小数点后两位).
【解答】解:=2≈2.83,
故答案为:2.83.
14.(3分)分式方程=的解是 x=5 .
【解答】解:去分母得:2x﹣2=x+3,
解得:x=5,
经检验x=5是分式方程的解.
故答案为:x=5
15.(3分)若等腰三角形的两边长分别是2cm和3cm,则这个等腰三角形的周长是 8或7 cm.
【解答】解:当2cm为底时,则其它两边都为3cm,
3cm、3cm、2cm可以构成三角形,
所以周长为8cm;
当3cm为底时,
其它两边为2cm和2cm,能构成三角形,
所以周长为7cm.
故答案为:8或7.
16.(3分)已知,,则x2+2xy+y2的值为 12 .
【解答】解:∵,,
∴x2+2xy+y2=(x+y)2=(+1+﹣1)2=(2)2=12;
故答案为:12.
17.(3分)某次列车平均提速vkm/h,用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km,可求得提速前列车的平均速度为 km/h.
【解答】解:设提速前列车的平均速度为xkm/h,根据题意可得:
=,
解得:x=.
故答案为:.
18.(3分)如图,在△ABC中,AB=5,BC=3,以点B为圆心,BC长为半径画弧,与AC交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,交AB于点G,连接DG,则△BDG的周长为 8 .
【解答】解:由题意知,BD=BC,直线EF为线段AD的垂直平分线,
∴AG=DG,
∴△BDG的周长为BD+DG+BG=BC+AG+BG=BC+AB=8.
故答案为:8.
三、解答题(其中19-21题各8分,22-24题各10分,25题12分,共计66分)
19.(8分)计算:
(1)(2a)3 b4÷12a3b2;
(2)(3x+1)(x+2).
【解答】解:(1)原式=8a3 b4÷12a3b2=;
(2)原式=3x2+6x+x+2=3x2+7x+2.
20.(8分)计算:
(1)×
(2)2﹣6+3.
【解答】解:(1)原式=3×5÷
=15÷
=15;
(2)原式=4﹣2+12
=14.
21.(8分)先化简,再求代数式的值,其中m为满足0<m<4的整数.
【解答】解:原式=
=
=m+3,
∵m﹣2≠0,m﹣3≠0,
∴m≠2,m≠3,
又∵m为满足0<m<4的整数,
∴m=1,
∴原式=1+3=4.
22.(10分)解方程与不等式:
(1)(x+2)(x﹣2)﹣(x﹣1)(x+5)=1;
(2)4(x+1)2﹣(2x+5)(2x﹣5)≤21.
【解答】解:x2﹣4﹣(x2+5x﹣x﹣5)=1,
x2﹣4﹣x2﹣5x+x+5=1,
﹣4x=0,
x=0;
(2)4(x2+2x+1)﹣(4x2﹣25)≤21,
4x2+8x+4﹣4x2+25≤21,
8x≤﹣8,
x≤﹣1.
23.(10分)如图,△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,﹣1),C(﹣3,2).
(1)已知△ABC和△A1B1C1关于x轴对称,点A1,B1,C1分别是点A,B,C的对称点,请直接写出点A1,B1,C1的坐标;
(2)在图中画出△ABC关于y轴对称的△A2B2C2.
【解答】解:(1)∵A(﹣4,1),B(﹣1,﹣1),C(﹣3,2),
∴A1(﹣4,﹣1),B1(﹣1,1),C1(﹣3,﹣2).
(2)如图,△A2B2C2即为所求.
24.(10分)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠550米,甲施工队施工5天后,增加施工人员,每天比原来多修建30米,再施工2天完成任务.甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建450米后,通过技术更新,每天比原来多修建25%,灌溉水渠完工时,两施工队修建的长度恰好相同.乙施工队原来每天修建灌溉水渠多少米?
【解答】解:(1)设甲施工队增加人员后每天修建灌溉水渠x米,则原计划每天施工(x﹣30)米,
由题意可得:5(x﹣30)+2x=550,
解得x=100,
答:甲施工队增加人员后每天修建灌溉水渠100米;
(2)设乙施工队原来每天修建灌溉水渠m米,则技术更新后每天修建水渠m(1+25%)=1.2m米,
由题意可得:+=,
解得m=90,
经检验,m=90是原分式方程的解,
答:乙施工队原来每天修建灌溉水渠90米.
25.(12分)已知:在△ABC中,∠ACB=90°,∠A=60°.点D在AB上,且AD=AC,连接CD.
(1)如图1,求证:BD=CD;
(2)过点D作△DEF,使∠DEF=90°,∠EDF=60°.连接CE并延长CE至点G,使EG=CE,连接BF,BG,FG.
①如图2,当点F在DB的延长线上时,求证:△BFG是等边三角形;
②如图3,AC=2,DE=1,若∠BFD+∠EFG=180°,求△BDF的面积.
【解答】(1)证明:∵DA=CA,∠A=60°,
∴△ACD是等边三角形,
∴AC=CD,∠ACD=∠A=60°,
∵∠ACB=90°,
∴∠ABC=90°﹣∠A=90°﹣∠ACD=90°﹣60°=30°,
∴∠ABC=∠BCD,
∴BD=CD;
(2)①证明:如图2,延长FE,DC交于点K,
∵∠FED=90°,
∴∠EFD=90°﹣∠FDE=30°,
∴∠K=∠KDA﹣∠DFK=60°﹣30°=30°,
∴∠K=∠DFK,
∴FD=KD,
又∵DB=DC,
∴CK=BF,
∵∠DEF=90°,
∴DE⊥FK
又∵DK=DF,
∴EK=EF,
又∵∠CEK=∠GEF,CE=EG,
∴△CEK≌△GEF(SAS),
∴FG=CK,∠GFK=∠K=30°,
∴FG=BF,∠GFB=∠GFK+∠DFK=30°+30°=60°,
∴△BFG是等边三角形;
②解:如图3延长DE至H,使EH=DE,连接FH,GH,过点B作BM⊥DF于点M,
∵CE=EG,∠CED=∠GEH,DE=EH,
∴△CDE≌△GHE(SAS),
∴GH=CD,∠CDE=∠GHE,
∵BD=CD,
∴GH=BD,
∵∠DEF=90°,
∴FE⊥DH,
又∵DE=EH,
∴FH=FD
又∵∠FDH=60°,
∴△DFH是等边三角形
∴∠DFH=∠DHF=60°,
∴∠EFH=90°﹣∠DHF=90°﹣60°=30°,
设∠FHC=α,
∴∠CDE=∠GHE=α+60°,
∴∠BDE=∠BDC﹣∠CDF=120°﹣(α+60°)=60°﹣α,
∴∠BDF=∠FDF﹣∠BDF=60°﹣(60°﹣α)=α,
∴∠BDF=∠FHG,
∴△BDF≌△GHF(SAS),
∴∠BFD=∠GFH,
令∠BFD=β,则∠GFH=β,
∴∠FFG=∠GFH+∠FFH=β+30°,
∵∠BFD+∠FFG=180°,
∴β+β+30°=180°,
∴β=75°,
∴∠BFD=75°,
在Rt△DEF中,∠DFE=30°,
∴DF=2DE=2,
又∵BD=CD=AD=2,
∴BD=DF,
∴∠DBF=∠BFD=75°,
∴∠BDF=180°﹣75°﹣75°=30°,
在Rt△BDM中,,
∴.
第1页(共1页)
同课章节目录
