黑龙江省哈尔滨市南岗区松雷中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市南岗区松雷中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1017.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 09:59:14 | ||
图片预览



文档简介
2023-2024学年黑龙江省哈尔滨市南岗区松雷中学九年级(上)开学数学试卷(五四学制)
一、选择题(每题3分,共30分)
1.(3分)﹣2的倒数是( )
A.﹣2 B.﹣ C. D.2
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.a6÷a2=a4 C.(a2)3=a5 D.a a3=a3
3.(3分)下列图形中,是轴对称图形的是( )
A.. B.
C. D.
4.(3分)下面几何体的左视图是( )
A. B. C. D.
5.(3分)下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③相等的圆心角所对的弧相等.其中真命题的是( )
A.①② B.②③ C.①③ D.①②③
6.(3分)AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
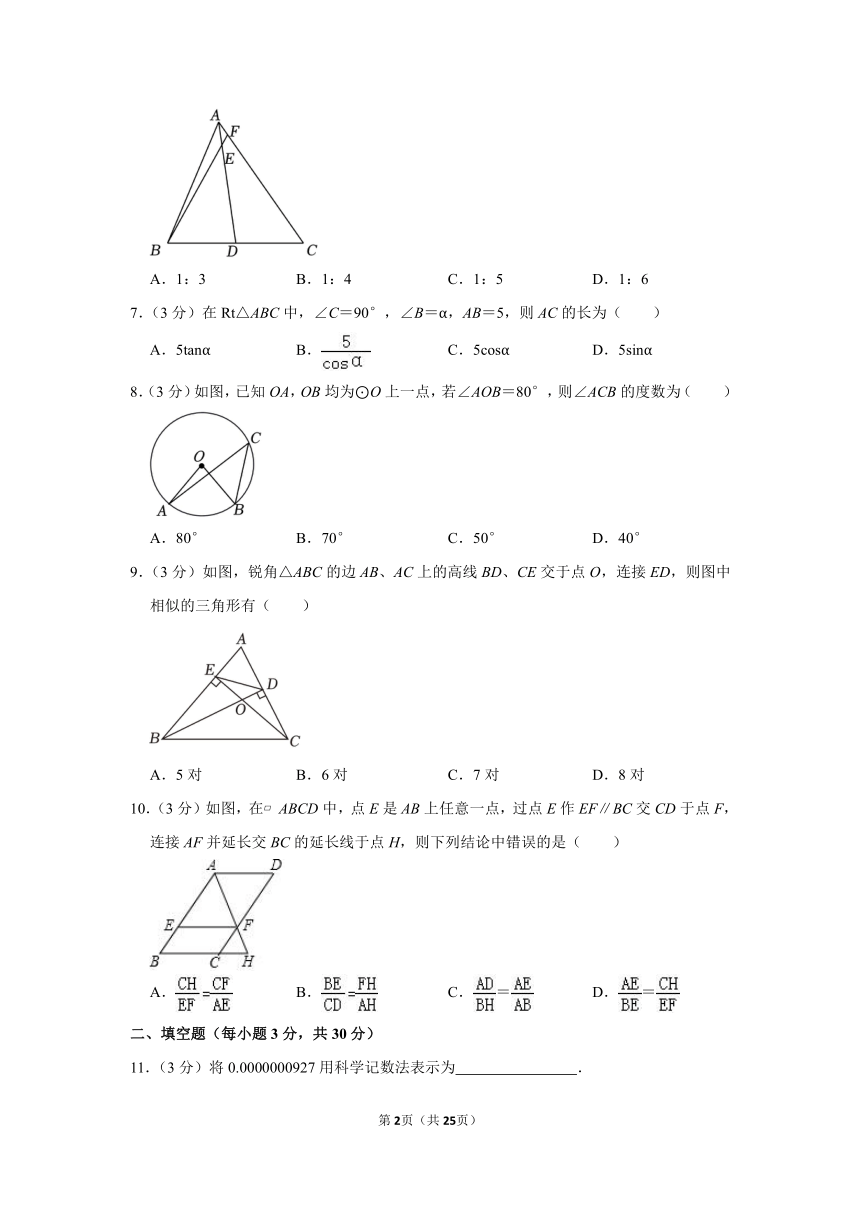
A.1:3 B.1:4 C.1:5 D.1:6
7.(3分)在Rt△ABC中,∠C=90°,∠B=α,AB=5,则AC的长为( )
A.5tanα B. C.5cosα D.5sinα
8.(3分)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB的度数为( )
A.80° B.70° C.50° D.40°
9.(3分)如图,锐角△ABC的边AB、AC上的高线BD、CE交于点O,连接ED,则图中相似的三角形有( )
A.5对 B.6对 C.7对 D.8对
10.(3分)如图,在 ABCD中,点E是AB上任意一点,过点E作EF∥BC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C.= D.=
二、填空题(每小题3分,共30分)
11.(3分)将0.0000000927用科学记数法表示为 .
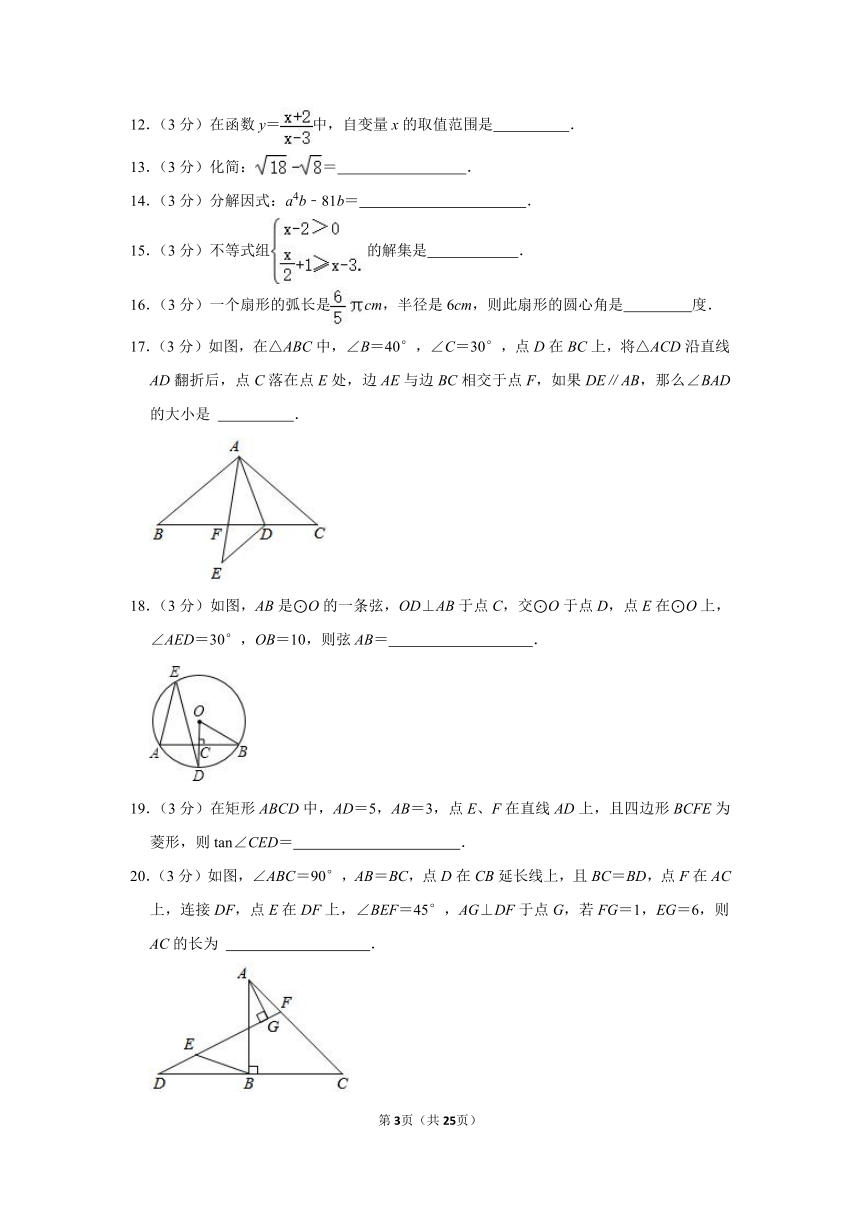
12.(3分)在函数y=中,自变量x的取值范围是 .
13.(3分)化简:= .
14.(3分)分解因式:a4b﹣81b= .
15.(3分)不等式组的解集是 .
16.(3分)一个扇形的弧长是cm,半径是6cm,则此扇形的圆心角是 度.
17.(3分)如图,在△ABC中,∠B=40°,∠C=30°,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE与边BC相交于点F,如果DE∥AB,那么∠BAD的大小是 .
18.(3分)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= .
19.(3分)在矩形ABCD中,AD=5,AB=3,点E、F在直线AD上,且四边形BCFE为菱形,则tan∠CED= .
20.(3分)如图,∠ABC=90°,AB=BC,点D在CB延长线上,且BC=BD,点F在AC上,连接DF,点E在DF上,∠BEF=45°,AG⊥DF于点G,若FG=1,EG=6,则AC的长为 .
三、解答题:(21、22每题7分,23、24每题8分,25、26、27每题10分,共60分)
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
22.(7分)如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A、B、C、D为顶点的四边形是轴对称图形.
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A、B、C、E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
23.(8分)某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
(1)求本次共抽查了多少人;
(2)请把条形统计图补充完整;
(3)已知该校有1200人,请根据样本估计全校最喜欢乒乓球的人数是多少?
24.(8分)如图1,已知Rt△ABC,∠ABC=90°,以AC、AB为边向形外作等边三角形ACD、ABF,连接CF、BD.
(1)求证:CF=BD;
(2)如图2,若∠BAC=30°,点H为AC的中点,连接FH、BH、DH,请直接写出与△ABC全等的所有三角形.
25.(10分)某学校计划从商店购买测温枪和洗手液,已知购买一个测温枪比购买一瓶洗手液多用20元,若用400元购买测温枪和用160元购买洗手液,则购买测温枪的个数是购买洗手液个数的一半.
(1)求购买一个测温枪、一瓶洗手液各需要多少元;
(2)经商谈,商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠,如果该学校需要洗手液个数是测温枪个数的2倍还多8个,且该学校购买测温枪和洗手液的总费用不超过670元,那么该学校最多可购买多少个测温枪?
26.(10分)已知△ABC内接于⊙O,点F是弧AC的中点,连接OF交AC于点H.
(1)如图1,求证:OF⊥AC;
(2)如图2,AD是△ABC的高,延长AD交⊙O于点K,若∠CAD=2∠BAD,求证:AK=AC;
(3)如图3,在(2)的条件下,延长FO交BD于点E,连接EK,点M在CH上,连接OM.若∠OMH=3∠DKE,BE=OH,AM=,求HF的长.
27.(10分)在平面直角坐标系中,点O为坐标原点,直线y=kx+6k交x轴于点B,交y轴于点A,AB=2AO.
(1)如图1,求k的值;
(2)如图2,点H在AB上,点F在OB上,连接FH、OH,且FH=OH,过点F作AB的垂线,垂足为点S,设点H的横坐标为t(﹣3<t<﹣1),线段SH的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段OH绕点O顺时针旋转60°得到线段OE,连接AE并延长交x轴于C,连接HC,点K是HC的中点,连接EK,当时,求△SHF的面积.
2023-2024学年黑龙江省哈尔滨市南岗区松雷中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每题3分,共30分)
1.(3分)﹣2的倒数是( )
A.﹣2 B.﹣ C. D.2
【解答】解:∵﹣2×=1.
∴﹣2的倒数是﹣,
故选:B.
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.a6÷a2=a4 C.(a2)3=a5 D.a a3=a3
【解答】解:A、2a与3b不是同类项,故A不符合题意.
B、原式=a4,故B符合题意.
C、原式=a6,故C不符合题意.
D、原式=a4,故D不符合题意.
故选:B.
3.(3分)下列图形中,是轴对称图形的是( )
A.. B.
C. D.
【解答】解:选项A、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项B能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
4.(3分)下面几何体的左视图是( )
A. B. C. D.
【解答】解:从左面看,看到的图形分为上下两层,上面一层左边有1个小正方形,下面一层有两个小正方形,即看到的图形为,
故选:A.
5.(3分)下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③相等的圆心角所对的弧相等.其中真命题的是( )
A.①② B.②③ C.①③ D.①②③
【解答】解:①由于圆沿着每条直径所在直线对折后能够完全重合,所以圆是轴对称图形;由于圆绕着圆心旋转180°后能与本身重合,所以圆是中心对称图形;所以此命题为真命题,故本选项正确;
②垂直于弦的直径平分弦,符合垂径定理,是真命题,故本选项正确;
③相等的圆心角所对的弧相等,说法不确切,应为“在同圆或等圆中,相等的圆心角所对的弧相等”,故本选项错误;
故选:A.
6.(3分)AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
A.1:3 B.1:4 C.1:5 D.1:6
【解答】解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴BD=DC,
∴FH=HC,
∵DH∥BF,
∴==,
∴AF:FC=1:6,
故选:D.
7.(3分)在Rt△ABC中,∠C=90°,∠B=α,AB=5,则AC的长为( )
A.5tanα B. C.5cosα D.5sinα
【解答】解:在Rt△ABC中,∠C=90°,
∵sinB=,
∴AC=AB sinB=5sinα,
故选:D.
8.(3分)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB的度数为( )
A.80° B.70° C.50° D.40°
【解答】解:由题意得,∠ACB=∠AOB=×80°=40°.
故选:D.
9.(3分)如图,锐角△ABC的边AB、AC上的高线BD、CE交于点O,连接ED,则图中相似的三角形有( )
A.5对 B.6对 C.7对 D.8对
【解答】解:∵BD⊥AC,CE⊥AB,
∴∠BEC=∠AEC=∠BDC=∠ADB=90°,
∴∠A+∠ABD=∠A+∠ACE,
∴∠ABD=∠ACE,
∴△ABD∽△ACE∽△BOE∽△COD,即有6对相似三角形,
∴,
又∵∠A=∠A,
∴△ADE∽△ABC,
∵,∠DOE=∠BOC,
∴△BOC∽△EOD,
故选:D.
10.(3分)如图,在 ABCD中,点E是AB上任意一点,过点E作EF∥BC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C.= D.=
【解答】解:∵四边形ABCD为平行四边形,EF∥BC,
∴AD=EF=BC,AE=DF,BE=CF.
A、∵AD∥CH,
∴△ADF∽△HCF,
∴=,即=,结论A正确;
B、∵AB∥CD,
∴△ABH∽△FCH,
∴=,即=,结论B正确;
C、∵AD∥BH,
∴△ADF∽△HBA,
∴=,即=,结论C正确;
D、∵AE∥CF,EF∥CH,
∴△FCH∽△AEF,
∴=,即=,结论D错误.
故选:D.
二、填空题(每小题3分,共30分)
11.(3分)将0.0000000927用科学记数法表示为 9.27×10﹣8 .
【解答】解:0.0000000927=9.27×10﹣8,
故答案为:9.27×10﹣8.
12.(3分)在函数y=中,自变量x的取值范围是 x≠3 .
【解答】解:由题意得,x﹣3≠0,
解得x≠3.
故答案为:x≠3.
13.(3分)化简:= .
【解答】解:原式=3﹣2=.
故答案为:.
14.(3分)分解因式:a4b﹣81b= b(a2+9)(a+3)(a﹣3) .
【解答】解:原式=b(a4﹣81)
=b(a2+9)(a2﹣9)
=b(a2+9)(a+3)(a﹣3).
故答案为:b(a2+9)(a+3)(a﹣3).
15.(3分)不等式组的解集是 2<x≤8 .
【解答】解:
∵解不等式①得:x>2,
解不等式②得:x≤8,
∴不等式组的解集为2<x≤8,
故答案为:2<x≤8.
16.(3分)一个扇形的弧长是cm,半径是6cm,则此扇形的圆心角是 36 度.
【解答】解:设扇形的圆心角为n.
由题意:π=,
解得n=36°,
故答案为36.
17.(3分)如图,在△ABC中,∠B=40°,∠C=30°,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE与边BC相交于点F,如果DE∥AB,那么∠BAD的大小是 70° .
【解答】解:在△ABC中,∠B=40°,∠C=30°,
∴∠BAC=180°﹣∠B﹣∠C=110°.
由折叠的性质可知:∠CAD=∠EAD,∠E=∠C=30°.
∵DE∥AB,
∴∠BAE=∠E=30°,
∴∠BAC=∠BAE+∠CAD+∠EAD,即110°=30°+2∠CAD,
∴∠CAD=40°.
∴∠BAD=∠BAC﹣∠CAD=70°,
故答案为:70°.
18.(3分)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= 10 .
【解答】解:∵OD⊥AB,
∴AC=BC,=,
∵∠AED=30°,
∴∠BOD=2∠AED=60°,
在RT△OBC中,sin∠COB=,
∴OB=10,
∴=,
∴AB=2BC=10.
故答案为10.
19.(3分)在矩形ABCD中,AD=5,AB=3,点E、F在直线AD上,且四边形BCFE为菱形,则tan∠CED= 3或 .
【解答】解:∵四边形ABCD是矩形,
∴AD=BC=5,AB=AD=3,∠BAD=∠CDA=90°,
∵四边形BCFE为菱形,
∴BE=EF=FC=BC=5,
分两种情况:
①如图,当点F在AD的延长线上时,
∴AE==4,
∴DE=AD﹣AE=5﹣4=1,
∴tan∠CED==3.
②如图,当点E在DA的延长线上时,
在Rt△CDF中,
DF===4,
∴ED=EF+DF=5+4=9,
∴tan∠CED=.
故答案为:3或.
20.(3分)如图,∠ABC=90°,AB=BC,点D在CB延长线上,且BC=BD,点F在AC上,连接DF,点E在DF上,∠BEF=45°,AG⊥DF于点G,若FG=1,EG=6,则AC的长为 3 .
【解答】解:连接AD,延长AG交BC于H,连接BG,
∵∠ABC=90°,AB=BC=BD,
∴△ABC,△ABD均为等腰直角三角形,
∴∠ADB=∠C=45°,∠DAB=∠BAC=45°,
∵AG⊥DF,
∴∠BAH+∠1=90°,
∵∠1=∠2,
∵∠BDM+∠2=90°,
∴∠BDM=∠BAH,
∴△BDM≌△BAH(ASA),
同理可得△ABG≌△DBE(ASA),
∴DE=AG,
设AG=x,DG=6+x,AG2=DG×FG,
即x2=6+x,
解得:x=3,
∴AD=3.
三、解答题:(21、22每题7分,23、24每题8分,25、26、27每题10分,共60分)
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
【解答】解:原式=
=
=,
x=4sin45°﹣2cos60°
=4×﹣2×
=,
∴当x=时,原式====.
22.(7分)如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A、B、C、D为顶点的四边形是轴对称图形.
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A、B、C、E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
【解答】解:(1)如图1所示:
(2)如图2所示:四边形ACBE的面积为:2×4=8.
23.(8分)某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
(1)求本次共抽查了多少人;
(2)请把条形统计图补充完整;
(3)已知该校有1200人,请根据样本估计全校最喜欢乒乓球的人数是多少?
【解答】解:(1)总人数=44÷44%=100人.
(2)B项目人数为8÷8%×20%=20人,
补全图形如下:
(3)1200×44%=528人,
全校最喜欢乒乓球的人数大约是528人.
24.(8分)如图1,已知Rt△ABC,∠ABC=90°,以AC、AB为边向形外作等边三角形ACD、ABF,连接CF、BD.
(1)求证:CF=BD;
(2)如图2,若∠BAC=30°,点H为AC的中点,连接FH、BH、DH,请直接写出与△ABC全等的所有三角形.
【解答】(1)证明:∵△ABF和△ACD都是等边三角形,
∴∠FAB=∠CAD=60°,AF=AB,AC=AD,
∴∠FAB+∠BAC=∠CAD+∠BAC,
∴∠FAC=∠BAD,
在△AFC和△ABD中,
∴△AFC≌△ABD,
∴CF=BD,
(2)与△ABC全等的三角形有:△FAH,△FBH,△DHA,△DHC.
理由:∵∠BAC=30°,∠FAB=60°,
∴∠FAH=90°,易知∠AFH=30°,
∴FH=2AH=AC,
∵BC=AH=CH,
∴Rt△FAH≌Rt△ABC,
在Rt△ADH中,∵AD=2AH=AC,
∴AH=BC,AD=AC,
∴Rt△DHA≌Rt△ABC,
同法可证△FHB,△DHC与△ABC全等.
25.(10分)某学校计划从商店购买测温枪和洗手液,已知购买一个测温枪比购买一瓶洗手液多用20元,若用400元购买测温枪和用160元购买洗手液,则购买测温枪的个数是购买洗手液个数的一半.
(1)求购买一个测温枪、一瓶洗手液各需要多少元;
(2)经商谈,商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠,如果该学校需要洗手液个数是测温枪个数的2倍还多8个,且该学校购买测温枪和洗手液的总费用不超过670元,那么该学校最多可购买多少个测温枪?
【解答】解:(1)设购买一瓶洗手液需要x元,则购买一个测温枪需要(x+20)元,
依题意,得:=×,
解得:x=5,
经检验,x=5是原方程的解,且符合题意,
∴x+20=25.
答:购买一个测温枪需要25元,购买一瓶洗手液需要5元.
(2)设该学校购买m个测温枪,则购买(2m+8)瓶洗手液,
依题意,得:25m+5(2m+8﹣m)≤670,
解得:m≤21.
答:该学校最多可购买21个测温枪.
26.(10分)已知△ABC内接于⊙O,点F是弧AC的中点,连接OF交AC于点H.
(1)如图1,求证:OF⊥AC;
(2)如图2,AD是△ABC的高,延长AD交⊙O于点K,若∠CAD=2∠BAD,求证:AK=AC;
(3)如图3,在(2)的条件下,延长FO交BD于点E,连接EK,点M在CH上,连接OM.若∠OMH=3∠DKE,BE=OH,AM=,求HF的长.
【解答】(1)证明:如图1,连接AO、CO,
∵点F是弧AC的中点,
∴,
∴∠AOF=∠COF,
∵OA=OC,
∴OF⊥AC;
(2)证明:如图2,连接KC,
∵∠CAD=2∠BAD,
∴设∠BAD=α,则∠CAD=2α,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠B=90°﹣α,∠ACB=90°﹣2α,
∴∠K=∠B=90°﹣α,
∵∠BCK=∠BAD=α,
∴∠ACK=∠ACB+∠BCK=90°﹣2α+α=90°﹣α,
∴∠AKC=∠ACK,
∴AC=AK;
(3)解:如图3,过点O分别作OG⊥AD于点G,ON⊥EC于点N,过点C作CQ⊥AB于Q,连接AO并延长交DC于点P,连接OK、OC,
则四边形DNOG为矩形,BN=CN,
∴DN=OG,OG∥BC,
∵AK=AC,OK=OC,OA=OA,
∴△AOK≌△AOC(SSS),
∴∠KAP=∠CAP=∠CAK=×2α=α,
∴∠BAD=∠KAO=∠OAC=α,
∵AD⊥BC,
∴BD=PD,
∵OH⊥AC,OG⊥AK,
∴OG=OH,
∵OH=BE,
∴OG=OH=BE,
∵∠APD=90°﹣α,∠EHC=90°,∠ACB=90°﹣2α,
∴∠PEO=180°﹣∠EHC﹣∠ECH=180°﹣90°﹣(90°﹣2α)=2α,
∴∠EOP=180°﹣∠APD﹣∠PEO=180°﹣(90°﹣α)﹣2α=90°﹣α,
∴∠EOP=∠EPO,
∴OE=EP,
设BE=m,DE=n,
则OG=OH=DN=BE=m,BD=EN=PD=m+n,
∴DC=CN+DN=BD+DN+DN=m+n+m+m=3m+n,
∴EC=DC+DE=3m+n+n=3m+2n,OE=EP=DE+DP=DE+BD=n+m+n=m+2n,EH=OE+OH=m+2n+m=2m+2n,
∵cos∠OEP==,
∴=,
解得:m=2n,
∴EN=3n,OE=4n,
由勾股定理得:ON===n,
∴tan∠PEO=tan2α===,
∴AD====3n,AC===4n,
∴AK=AC=4n,
∴AG=GK=2n=AH=HC,
∴DK=n,
∴tan∠EKD===tanα,
∵AB===6n,
∴S△ABC=×AB CQ=×BC AD,
∴CQ=n,
∴AQ===n,
∵∠OMH=3∠DKE,
∴∠OMH=∠BAC,
∴tan∠OMH=tan∠BAC=,
∴,
∴,
∵,
∴n=2,
∴OH=4,AH=4,
∴AO===8,
∴.
27.(10分)在平面直角坐标系中,点O为坐标原点,直线y=kx+6k交x轴于点B,交y轴于点A,AB=2AO.
(1)如图1,求k的值;
(2)如图2,点H在AB上,点F在OB上,连接FH、OH,且FH=OH,过点F作AB的垂线,垂足为点S,设点H的横坐标为t(﹣3<t<﹣1),线段SH的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段OH绕点O顺时针旋转60°得到线段OE,连接AE并延长交x轴于C,连接HC,点K是HC的中点,连接EK,当时,求△SHF的面积.
【解答】解:(1)由y=kx+6k=k(x+6),
则B(﹣6,0),
由 得:∠ABO=30°,
则==,
则OA=2,
则点A(0,2),
将点A的坐标代入y=kx+6k并解得:;
(2)由(1)知直线AB的表达式为:y=x+2,
过点H作HK⊥x轴,HG⊥y轴,如图2,
设点H(t,t+2),
在Rt△BHK中,BH=2HK=+4,
因为HF=HO,
所以FK=OK=HG=﹣t,
则BF=6﹣OF=6﹣(﹣2t)=6+2t,
Rt△BFS中,SF=BF=3+t,而BS=SF=3+t,
所以d=HB﹣BS=+4﹣(3+t)=﹣t+(﹣3<t<﹣1);
(3)如图3,线段OH绕点O顺时针旋转60°得到线段OE,则△HEO为等边三角形,
则∠HAO=∠HEO=60°,
则点A、H、O、E四点共圆,则∠OAC=60°,
根据图象的对称性,则OB=OC=6,
因为K是HC的中点所以HK=CK,
所以且OK∥AB,
延长OK交AC于点L,
∵点K是HC的中点,点O是BC的中点,
则OK是△CBH的中位线,
则KL是△CAH的中位线,
则,
则LO是△AOC的直线,
则△AOL等边三角形,则OL=AO,
∵∠HOA+∠AOE=∠AOE+∠EOL=60°,
∴∠HOA=∠EOL,
∵OH=OE,
∴△AHO≌△LEO(SAS),
∴EL=AH=2KL,
∵∠OLA=60°,
过点E作EK′⊥LO,则LK′=EL,
则点E′、E重合,即EK⊥LK,
∵∠AGH=∠EKL=90°,AH=EL,∠ELK=∠HAG=60°
△AHG≌△EKL(AAS),
所以EK=HG=﹣t,
∵=,而tan∠OEK==,
当时,
则=×,
解得:t1=1(舍)t2=﹣2
所以.
第1页(共1页)
一、选择题(每题3分,共30分)
1.(3分)﹣2的倒数是( )
A.﹣2 B.﹣ C. D.2
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.a6÷a2=a4 C.(a2)3=a5 D.a a3=a3
3.(3分)下列图形中,是轴对称图形的是( )
A.. B.
C. D.
4.(3分)下面几何体的左视图是( )
A. B. C. D.
5.(3分)下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③相等的圆心角所对的弧相等.其中真命题的是( )
A.①② B.②③ C.①③ D.①②③
6.(3分)AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
A.1:3 B.1:4 C.1:5 D.1:6
7.(3分)在Rt△ABC中,∠C=90°,∠B=α,AB=5,则AC的长为( )
A.5tanα B. C.5cosα D.5sinα
8.(3分)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB的度数为( )
A.80° B.70° C.50° D.40°
9.(3分)如图,锐角△ABC的边AB、AC上的高线BD、CE交于点O,连接ED,则图中相似的三角形有( )
A.5对 B.6对 C.7对 D.8对
10.(3分)如图,在 ABCD中,点E是AB上任意一点,过点E作EF∥BC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C.= D.=
二、填空题(每小题3分,共30分)
11.(3分)将0.0000000927用科学记数法表示为 .
12.(3分)在函数y=中,自变量x的取值范围是 .
13.(3分)化简:= .
14.(3分)分解因式:a4b﹣81b= .
15.(3分)不等式组的解集是 .
16.(3分)一个扇形的弧长是cm,半径是6cm,则此扇形的圆心角是 度.
17.(3分)如图,在△ABC中,∠B=40°,∠C=30°,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE与边BC相交于点F,如果DE∥AB,那么∠BAD的大小是 .
18.(3分)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= .
19.(3分)在矩形ABCD中,AD=5,AB=3,点E、F在直线AD上,且四边形BCFE为菱形,则tan∠CED= .
20.(3分)如图,∠ABC=90°,AB=BC,点D在CB延长线上,且BC=BD,点F在AC上,连接DF,点E在DF上,∠BEF=45°,AG⊥DF于点G,若FG=1,EG=6,则AC的长为 .
三、解答题:(21、22每题7分,23、24每题8分,25、26、27每题10分,共60分)
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
22.(7分)如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A、B、C、D为顶点的四边形是轴对称图形.
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A、B、C、E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
23.(8分)某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
(1)求本次共抽查了多少人;
(2)请把条形统计图补充完整;
(3)已知该校有1200人,请根据样本估计全校最喜欢乒乓球的人数是多少?
24.(8分)如图1,已知Rt△ABC,∠ABC=90°,以AC、AB为边向形外作等边三角形ACD、ABF,连接CF、BD.
(1)求证:CF=BD;
(2)如图2,若∠BAC=30°,点H为AC的中点,连接FH、BH、DH,请直接写出与△ABC全等的所有三角形.
25.(10分)某学校计划从商店购买测温枪和洗手液,已知购买一个测温枪比购买一瓶洗手液多用20元,若用400元购买测温枪和用160元购买洗手液,则购买测温枪的个数是购买洗手液个数的一半.
(1)求购买一个测温枪、一瓶洗手液各需要多少元;
(2)经商谈,商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠,如果该学校需要洗手液个数是测温枪个数的2倍还多8个,且该学校购买测温枪和洗手液的总费用不超过670元,那么该学校最多可购买多少个测温枪?
26.(10分)已知△ABC内接于⊙O,点F是弧AC的中点,连接OF交AC于点H.
(1)如图1,求证:OF⊥AC;
(2)如图2,AD是△ABC的高,延长AD交⊙O于点K,若∠CAD=2∠BAD,求证:AK=AC;
(3)如图3,在(2)的条件下,延长FO交BD于点E,连接EK,点M在CH上,连接OM.若∠OMH=3∠DKE,BE=OH,AM=,求HF的长.
27.(10分)在平面直角坐标系中,点O为坐标原点,直线y=kx+6k交x轴于点B,交y轴于点A,AB=2AO.
(1)如图1,求k的值;
(2)如图2,点H在AB上,点F在OB上,连接FH、OH,且FH=OH,过点F作AB的垂线,垂足为点S,设点H的横坐标为t(﹣3<t<﹣1),线段SH的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段OH绕点O顺时针旋转60°得到线段OE,连接AE并延长交x轴于C,连接HC,点K是HC的中点,连接EK,当时,求△SHF的面积.
2023-2024学年黑龙江省哈尔滨市南岗区松雷中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每题3分,共30分)
1.(3分)﹣2的倒数是( )
A.﹣2 B.﹣ C. D.2
【解答】解:∵﹣2×=1.
∴﹣2的倒数是﹣,
故选:B.
2.(3分)下列计算正确的是( )
A.2a+3b=5ab B.a6÷a2=a4 C.(a2)3=a5 D.a a3=a3
【解答】解:A、2a与3b不是同类项,故A不符合题意.
B、原式=a4,故B符合题意.
C、原式=a6,故C不符合题意.
D、原式=a4,故D不符合题意.
故选:B.
3.(3分)下列图形中,是轴对称图形的是( )
A.. B.
C. D.
【解答】解:选项A、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项B能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
4.(3分)下面几何体的左视图是( )
A. B. C. D.
【解答】解:从左面看,看到的图形分为上下两层,上面一层左边有1个小正方形,下面一层有两个小正方形,即看到的图形为,
故选:A.
5.(3分)下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③相等的圆心角所对的弧相等.其中真命题的是( )
A.①② B.②③ C.①③ D.①②③
【解答】解:①由于圆沿着每条直径所在直线对折后能够完全重合,所以圆是轴对称图形;由于圆绕着圆心旋转180°后能与本身重合,所以圆是中心对称图形;所以此命题为真命题,故本选项正确;
②垂直于弦的直径平分弦,符合垂径定理,是真命题,故本选项正确;
③相等的圆心角所对的弧相等,说法不确切,应为“在同圆或等圆中,相等的圆心角所对的弧相等”,故本选项错误;
故选:A.
6.(3分)AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
A.1:3 B.1:4 C.1:5 D.1:6
【解答】解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴BD=DC,
∴FH=HC,
∵DH∥BF,
∴==,
∴AF:FC=1:6,
故选:D.
7.(3分)在Rt△ABC中,∠C=90°,∠B=α,AB=5,则AC的长为( )
A.5tanα B. C.5cosα D.5sinα
【解答】解:在Rt△ABC中,∠C=90°,
∵sinB=,
∴AC=AB sinB=5sinα,
故选:D.
8.(3分)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB的度数为( )
A.80° B.70° C.50° D.40°
【解答】解:由题意得,∠ACB=∠AOB=×80°=40°.
故选:D.
9.(3分)如图,锐角△ABC的边AB、AC上的高线BD、CE交于点O,连接ED,则图中相似的三角形有( )
A.5对 B.6对 C.7对 D.8对
【解答】解:∵BD⊥AC,CE⊥AB,
∴∠BEC=∠AEC=∠BDC=∠ADB=90°,
∴∠A+∠ABD=∠A+∠ACE,
∴∠ABD=∠ACE,
∴△ABD∽△ACE∽△BOE∽△COD,即有6对相似三角形,
∴,
又∵∠A=∠A,
∴△ADE∽△ABC,
∵,∠DOE=∠BOC,
∴△BOC∽△EOD,
故选:D.
10.(3分)如图,在 ABCD中,点E是AB上任意一点,过点E作EF∥BC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C.= D.=
【解答】解:∵四边形ABCD为平行四边形,EF∥BC,
∴AD=EF=BC,AE=DF,BE=CF.
A、∵AD∥CH,
∴△ADF∽△HCF,
∴=,即=,结论A正确;
B、∵AB∥CD,
∴△ABH∽△FCH,
∴=,即=,结论B正确;
C、∵AD∥BH,
∴△ADF∽△HBA,
∴=,即=,结论C正确;
D、∵AE∥CF,EF∥CH,
∴△FCH∽△AEF,
∴=,即=,结论D错误.
故选:D.
二、填空题(每小题3分,共30分)
11.(3分)将0.0000000927用科学记数法表示为 9.27×10﹣8 .
【解答】解:0.0000000927=9.27×10﹣8,
故答案为:9.27×10﹣8.
12.(3分)在函数y=中,自变量x的取值范围是 x≠3 .
【解答】解:由题意得,x﹣3≠0,
解得x≠3.
故答案为:x≠3.
13.(3分)化简:= .
【解答】解:原式=3﹣2=.
故答案为:.
14.(3分)分解因式:a4b﹣81b= b(a2+9)(a+3)(a﹣3) .
【解答】解:原式=b(a4﹣81)
=b(a2+9)(a2﹣9)
=b(a2+9)(a+3)(a﹣3).
故答案为:b(a2+9)(a+3)(a﹣3).
15.(3分)不等式组的解集是 2<x≤8 .
【解答】解:
∵解不等式①得:x>2,
解不等式②得:x≤8,
∴不等式组的解集为2<x≤8,
故答案为:2<x≤8.
16.(3分)一个扇形的弧长是cm,半径是6cm,则此扇形的圆心角是 36 度.
【解答】解:设扇形的圆心角为n.
由题意:π=,
解得n=36°,
故答案为36.
17.(3分)如图,在△ABC中,∠B=40°,∠C=30°,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE与边BC相交于点F,如果DE∥AB,那么∠BAD的大小是 70° .
【解答】解:在△ABC中,∠B=40°,∠C=30°,
∴∠BAC=180°﹣∠B﹣∠C=110°.
由折叠的性质可知:∠CAD=∠EAD,∠E=∠C=30°.
∵DE∥AB,
∴∠BAE=∠E=30°,
∴∠BAC=∠BAE+∠CAD+∠EAD,即110°=30°+2∠CAD,
∴∠CAD=40°.
∴∠BAD=∠BAC﹣∠CAD=70°,
故答案为:70°.
18.(3分)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB= 10 .
【解答】解:∵OD⊥AB,
∴AC=BC,=,
∵∠AED=30°,
∴∠BOD=2∠AED=60°,
在RT△OBC中,sin∠COB=,
∴OB=10,
∴=,
∴AB=2BC=10.
故答案为10.
19.(3分)在矩形ABCD中,AD=5,AB=3,点E、F在直线AD上,且四边形BCFE为菱形,则tan∠CED= 3或 .
【解答】解:∵四边形ABCD是矩形,
∴AD=BC=5,AB=AD=3,∠BAD=∠CDA=90°,
∵四边形BCFE为菱形,
∴BE=EF=FC=BC=5,
分两种情况:
①如图,当点F在AD的延长线上时,
∴AE==4,
∴DE=AD﹣AE=5﹣4=1,
∴tan∠CED==3.
②如图,当点E在DA的延长线上时,
在Rt△CDF中,
DF===4,
∴ED=EF+DF=5+4=9,
∴tan∠CED=.
故答案为:3或.
20.(3分)如图,∠ABC=90°,AB=BC,点D在CB延长线上,且BC=BD,点F在AC上,连接DF,点E在DF上,∠BEF=45°,AG⊥DF于点G,若FG=1,EG=6,则AC的长为 3 .
【解答】解:连接AD,延长AG交BC于H,连接BG,
∵∠ABC=90°,AB=BC=BD,
∴△ABC,△ABD均为等腰直角三角形,
∴∠ADB=∠C=45°,∠DAB=∠BAC=45°,
∵AG⊥DF,
∴∠BAH+∠1=90°,
∵∠1=∠2,
∵∠BDM+∠2=90°,
∴∠BDM=∠BAH,
∴△BDM≌△BAH(ASA),
同理可得△ABG≌△DBE(ASA),
∴DE=AG,
设AG=x,DG=6+x,AG2=DG×FG,
即x2=6+x,
解得:x=3,
∴AD=3.
三、解答题:(21、22每题7分,23、24每题8分,25、26、27每题10分,共60分)
21.(7分)先化简,再求值的值,其中x=4sin45°﹣2cos60°.
【解答】解:原式=
=
=,
x=4sin45°﹣2cos60°
=4×﹣2×
=,
∴当x=时,原式====.
22.(7分)如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A、B、C、D为顶点的四边形是轴对称图形.
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A、B、C、E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
【解答】解:(1)如图1所示:
(2)如图2所示:四边形ACBE的面积为:2×4=8.
23.(8分)某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
(1)求本次共抽查了多少人;
(2)请把条形统计图补充完整;
(3)已知该校有1200人,请根据样本估计全校最喜欢乒乓球的人数是多少?
【解答】解:(1)总人数=44÷44%=100人.
(2)B项目人数为8÷8%×20%=20人,
补全图形如下:
(3)1200×44%=528人,
全校最喜欢乒乓球的人数大约是528人.
24.(8分)如图1,已知Rt△ABC,∠ABC=90°,以AC、AB为边向形外作等边三角形ACD、ABF,连接CF、BD.
(1)求证:CF=BD;
(2)如图2,若∠BAC=30°,点H为AC的中点,连接FH、BH、DH,请直接写出与△ABC全等的所有三角形.
【解答】(1)证明:∵△ABF和△ACD都是等边三角形,
∴∠FAB=∠CAD=60°,AF=AB,AC=AD,
∴∠FAB+∠BAC=∠CAD+∠BAC,
∴∠FAC=∠BAD,
在△AFC和△ABD中,
∴△AFC≌△ABD,
∴CF=BD,
(2)与△ABC全等的三角形有:△FAH,△FBH,△DHA,△DHC.
理由:∵∠BAC=30°,∠FAB=60°,
∴∠FAH=90°,易知∠AFH=30°,
∴FH=2AH=AC,
∵BC=AH=CH,
∴Rt△FAH≌Rt△ABC,
在Rt△ADH中,∵AD=2AH=AC,
∴AH=BC,AD=AC,
∴Rt△DHA≌Rt△ABC,
同法可证△FHB,△DHC与△ABC全等.
25.(10分)某学校计划从商店购买测温枪和洗手液,已知购买一个测温枪比购买一瓶洗手液多用20元,若用400元购买测温枪和用160元购买洗手液,则购买测温枪的个数是购买洗手液个数的一半.
(1)求购买一个测温枪、一瓶洗手液各需要多少元;
(2)经商谈,商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠,如果该学校需要洗手液个数是测温枪个数的2倍还多8个,且该学校购买测温枪和洗手液的总费用不超过670元,那么该学校最多可购买多少个测温枪?
【解答】解:(1)设购买一瓶洗手液需要x元,则购买一个测温枪需要(x+20)元,
依题意,得:=×,
解得:x=5,
经检验,x=5是原方程的解,且符合题意,
∴x+20=25.
答:购买一个测温枪需要25元,购买一瓶洗手液需要5元.
(2)设该学校购买m个测温枪,则购买(2m+8)瓶洗手液,
依题意,得:25m+5(2m+8﹣m)≤670,
解得:m≤21.
答:该学校最多可购买21个测温枪.
26.(10分)已知△ABC内接于⊙O,点F是弧AC的中点,连接OF交AC于点H.
(1)如图1,求证:OF⊥AC;
(2)如图2,AD是△ABC的高,延长AD交⊙O于点K,若∠CAD=2∠BAD,求证:AK=AC;
(3)如图3,在(2)的条件下,延长FO交BD于点E,连接EK,点M在CH上,连接OM.若∠OMH=3∠DKE,BE=OH,AM=,求HF的长.
【解答】(1)证明:如图1,连接AO、CO,
∵点F是弧AC的中点,
∴,
∴∠AOF=∠COF,
∵OA=OC,
∴OF⊥AC;
(2)证明:如图2,连接KC,
∵∠CAD=2∠BAD,
∴设∠BAD=α,则∠CAD=2α,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠B=90°﹣α,∠ACB=90°﹣2α,
∴∠K=∠B=90°﹣α,
∵∠BCK=∠BAD=α,
∴∠ACK=∠ACB+∠BCK=90°﹣2α+α=90°﹣α,
∴∠AKC=∠ACK,
∴AC=AK;
(3)解:如图3,过点O分别作OG⊥AD于点G,ON⊥EC于点N,过点C作CQ⊥AB于Q,连接AO并延长交DC于点P,连接OK、OC,
则四边形DNOG为矩形,BN=CN,
∴DN=OG,OG∥BC,
∵AK=AC,OK=OC,OA=OA,
∴△AOK≌△AOC(SSS),
∴∠KAP=∠CAP=∠CAK=×2α=α,
∴∠BAD=∠KAO=∠OAC=α,
∵AD⊥BC,
∴BD=PD,
∵OH⊥AC,OG⊥AK,
∴OG=OH,
∵OH=BE,
∴OG=OH=BE,
∵∠APD=90°﹣α,∠EHC=90°,∠ACB=90°﹣2α,
∴∠PEO=180°﹣∠EHC﹣∠ECH=180°﹣90°﹣(90°﹣2α)=2α,
∴∠EOP=180°﹣∠APD﹣∠PEO=180°﹣(90°﹣α)﹣2α=90°﹣α,
∴∠EOP=∠EPO,
∴OE=EP,
设BE=m,DE=n,
则OG=OH=DN=BE=m,BD=EN=PD=m+n,
∴DC=CN+DN=BD+DN+DN=m+n+m+m=3m+n,
∴EC=DC+DE=3m+n+n=3m+2n,OE=EP=DE+DP=DE+BD=n+m+n=m+2n,EH=OE+OH=m+2n+m=2m+2n,
∵cos∠OEP==,
∴=,
解得:m=2n,
∴EN=3n,OE=4n,
由勾股定理得:ON===n,
∴tan∠PEO=tan2α===,
∴AD====3n,AC===4n,
∴AK=AC=4n,
∴AG=GK=2n=AH=HC,
∴DK=n,
∴tan∠EKD===tanα,
∵AB===6n,
∴S△ABC=×AB CQ=×BC AD,
∴CQ=n,
∴AQ===n,
∵∠OMH=3∠DKE,
∴∠OMH=∠BAC,
∴tan∠OMH=tan∠BAC=,
∴,
∴,
∵,
∴n=2,
∴OH=4,AH=4,
∴AO===8,
∴.
27.(10分)在平面直角坐标系中,点O为坐标原点,直线y=kx+6k交x轴于点B,交y轴于点A,AB=2AO.
(1)如图1,求k的值;
(2)如图2,点H在AB上,点F在OB上,连接FH、OH,且FH=OH,过点F作AB的垂线,垂足为点S,设点H的横坐标为t(﹣3<t<﹣1),线段SH的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段OH绕点O顺时针旋转60°得到线段OE,连接AE并延长交x轴于C,连接HC,点K是HC的中点,连接EK,当时,求△SHF的面积.
【解答】解:(1)由y=kx+6k=k(x+6),
则B(﹣6,0),
由 得:∠ABO=30°,
则==,
则OA=2,
则点A(0,2),
将点A的坐标代入y=kx+6k并解得:;
(2)由(1)知直线AB的表达式为:y=x+2,
过点H作HK⊥x轴,HG⊥y轴,如图2,
设点H(t,t+2),
在Rt△BHK中,BH=2HK=+4,
因为HF=HO,
所以FK=OK=HG=﹣t,
则BF=6﹣OF=6﹣(﹣2t)=6+2t,
Rt△BFS中,SF=BF=3+t,而BS=SF=3+t,
所以d=HB﹣BS=+4﹣(3+t)=﹣t+(﹣3<t<﹣1);
(3)如图3,线段OH绕点O顺时针旋转60°得到线段OE,则△HEO为等边三角形,
则∠HAO=∠HEO=60°,
则点A、H、O、E四点共圆,则∠OAC=60°,
根据图象的对称性,则OB=OC=6,
因为K是HC的中点所以HK=CK,
所以且OK∥AB,
延长OK交AC于点L,
∵点K是HC的中点,点O是BC的中点,
则OK是△CBH的中位线,
则KL是△CAH的中位线,
则,
则LO是△AOC的直线,
则△AOL等边三角形,则OL=AO,
∵∠HOA+∠AOE=∠AOE+∠EOL=60°,
∴∠HOA=∠EOL,
∵OH=OE,
∴△AHO≌△LEO(SAS),
∴EL=AH=2KL,
∵∠OLA=60°,
过点E作EK′⊥LO,则LK′=EL,
则点E′、E重合,即EK⊥LK,
∵∠AGH=∠EKL=90°,AH=EL,∠ELK=∠HAG=60°
△AHG≌△EKL(AAS),
所以EK=HG=﹣t,
∵=,而tan∠OEK==,
当时,
则=×,
解得:t1=1(舍)t2=﹣2
所以.
第1页(共1页)
同课章节目录
