黑龙江省哈尔滨市南岗区松雷中学2023-2024学年七年级(上)开学数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市南岗区松雷中学2023-2024学年七年级(上)开学数学试卷(五四学制)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 538.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览




文档简介
2023-2024学年黑龙江省哈尔滨市南岗区松雷中学七年级(上)开学数学试卷(五四学制)
一、选择题(每小题3分,共计24分)
1.(3分)下列方程中,是一元一次方程的是( )
A.x2+2x=3 B.=x C.4x+y=1 D.3x﹣5=3
2.(3分)为了考察某市初中3500名毕业生的数学成绩,从中抽取20本试卷,每本30份,在这个问题中,样本容量是( )
A.3500 B.20 C.30 D.600
3.(3分)下列变形中正确的是( )
A.若x+3=5﹣3x,x+3x=5+3
B.若m=n,则am=an
C.若a=b,则a+c=b﹣c
D.若x=y,则=
4.(3分)下面四个图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
5.(3分)把方程=1﹣去分母后,正确的结果是( )
A.2x﹣1=1﹣(3﹣x) B.2(2x﹣1)=1﹣(3﹣x)
C.2(2x﹣1)=8﹣(3﹣x) D.2(2x﹣1)=8﹣3﹣x
6.(3分)某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母正好配套,设有x名工人生产螺钉,其他工人生产螺母,则根据题意可列方程为( )
A.2000x=1200(22﹣x) B.2×1200x=2000(22﹣x)
C.2×2000x=1200(22﹣x) D.1200x=2000(22﹣x)
7.(3分)有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.|a|>|b| B.ab>0 C.a+b>0 D.|a﹣b|>1
8.(3分)下列说法中错误的有( )个.
①多项式3x2 2x+1的一次项系数是2;
②单项式的系数是﹣2;
③单项式和多项式统称为整式;
④若x2my3 与2x4yn是同类项,那么m﹣n=﹣1.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计24分)
9.(3分)新疆的总面积约为1660000平方公里,是中国面积最大的省区,约占我国国土面积的六分之一,1660000用科学记数法可表示为 .
10.(3分)计算:22°17′×5= .
11.(3分)用四舍五入法把0.0568精确到千分位为 .
12.(3分)若∠1的对顶角是∠2,∠2的补角是∠3,∠3=54°,则∠1= .
13.(3分)若与互为相反数,则a的值是 .
14.(3分)某班级原来女生人数是全班人数的,调入4名女生后,女生人数是全班人数的一半,原来全班共有 人.
15.(3分)如图,直线AB和CD相交于O,OA平分∠COE,∠COE:∠BOE=2:5,则∠EOD的度数为 .
16.(3分)直线AB上有两点C、D,点C在A、B之间,满足CA=3CB,,若AB=20,则BD= .
三、解答题(其中17-18题各6分,19-23题各8分,24-25题各10分,共计72分)
17.(6分)计算:
(1)﹣52+(﹣7)×(﹣9)﹣16+(﹣2)3;
(2).
18.(6分)解方程
(1)1﹣3(8﹣x)=﹣2(15﹣2x);
(2)1=﹣x.
19.(8分)先化简,再求值:,其中.
20.(8分)如图所示,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.请在括号里填上推理依据.
证明:∵∠1+∠2=180°(已知),
∠1+∠4=180°( ),
∴∠2=∠4( ),
∴AB∥EG( ),
∴∠3= ,
又∵∠3=∠B(已知),
∴∠ =∠ ( ),
∴DE∥BC,
∴∠AED=∠C( ).
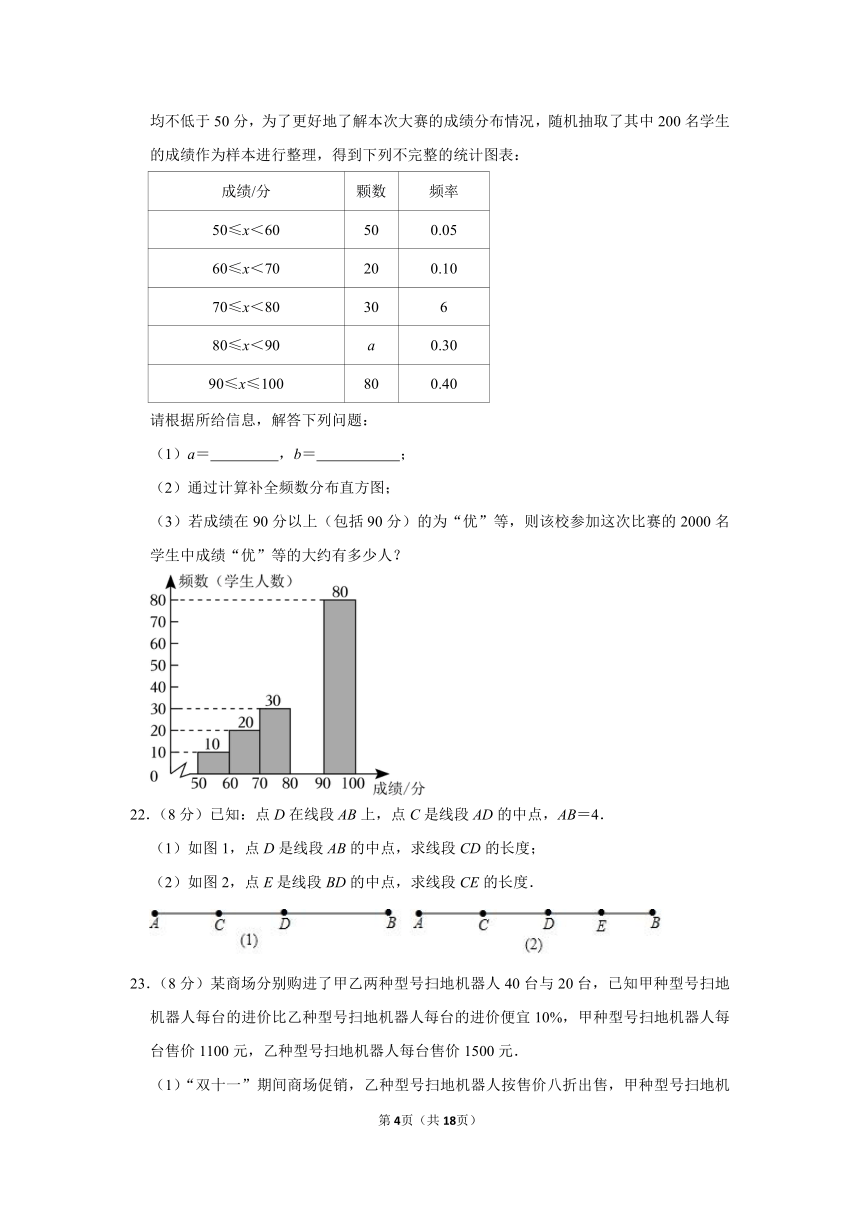
21.(8分)中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校2000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩/分 颗数 频率
50≤x<60 50 0.05
60≤x<70 20 0.10
70≤x<80 30 6
80≤x<90 a 0.30
90≤x≤100 80 0.40
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)通过计算补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的2000名学生中成绩“优”等的大约有多少人?
22.(8分)已知:点D在线段AB上,点C是线段AD的中点,AB=4.
(1)如图1,点D是线段AB的中点,求线段CD的长度;
(2)如图2,点E是线段BD的中点,求线段CE的长度.
23.(8分)某商场分别购进了甲乙两种型号扫地机器人40台与20台,已知甲种型号扫地机器人每台的进价比乙种型号扫地机器人每台的进价便宜10%,甲种型号扫地机器人每台售价1100元,乙种型号扫地机器人每台售价1500元.
(1)“双十一”期间商场促销,乙种型号扫地机器人按售价八折出售,甲种型号扫地机器人按原价销售.某公司一共花了10300元买了甲乙两种型号扫地机器人共9台.问某公司甲、乙两种型号扫地机器人各买了多少台?
(2)在(1)的条件下甲乙两种型号扫地机器人销售一空,甲种型号扫地机器人利润是乙种型号扫地机器人利润的2倍.问甲乙两种型号扫地机器人每台进价各是多少元?
24.(10分)阅读下列材料,并解决相应问题:
观察下面一列数:1,2,4,8,…我们发现,这一列数从第2项起,每一项与它前一项的比都等于2.一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比.
(1)如果一个等比数列的第2项是12,第3项是18,则这个等比数列的第1项是 ,第4项是 ;
(2)为了求等比数列1,2,4,8,…的前2024项的和,可以用如下的方法:求此等比数列前2024项的和,即为求1+2+22+23+…+22023的值,可令S=1+2+22+23+…+22023,则2S=2+22+23+24+…22024,因此2S﹣S=22024﹣1,所以S=1+2+22+23+…+22023=22024﹣1,请仿照以上材料,求出1+6+62+63+…+62023的值,并写明求解过程.
25.(10分)如图1,O是直线AB上的一点,OC⊥OD,OE平分∠BOC.
(1)若∠AOD=35°,求∠BOE的度数;
(2)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.
①探究∠AOC和∠DOE的度数之间的关系,并说明理由;
②在∠AOC的内部有一条射线OF,∠BOE内部有一条射线OM,且3∠AOD﹣∠AOF+2∠MOE=13∠COE+∠AOF,试确定∠FOM与∠DOE的度数之间的关系,并说明理由.
2023-2024学年黑龙江省哈尔滨市南岗区松雷中学七年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计24分)
1.(3分)下列方程中,是一元一次方程的是( )
A.x2+2x=3 B.=x C.4x+y=1 D.3x﹣5=3
【解答】解:A、含有未知数项的最高次数是2,它不是一元一次方程,故本选项不符合题意;
B、它不是整式方程,不是一元一次方程,故本选项不符合题意;
C、含有2个未知数,不是一元一次方程,故本选项不符合题意;
D、符合一元一次方程的定义,故本选项符合题意.
故选:D.
2.(3分)为了考察某市初中3500名毕业生的数学成绩,从中抽取20本试卷,每本30份,在这个问题中,样本容量是( )
A.3500 B.20 C.30 D.600
【解答】解:为了考察某市初中3500名毕业生的数学成绩,从中抽取20本试卷,每本30份,在这个问题中,样本容量是30×20=600,
故选:D.
3.(3分)下列变形中正确的是( )
A.若x+3=5﹣3x,x+3x=5+3
B.若m=n,则am=an
C.若a=b,则a+c=b﹣c
D.若x=y,则=
【解答】解:A.∵若x+3=5﹣3x,则x+3x=5﹣3,故A选项不正确;
B.若m=n,则am=an,故B选项正确;
C.若a=b,则a+c=b+c,故C选项不正确;
D.若x=y,则=(m≠﹣1),故D选项不正确.
故选:B.
4.(3分)下面四个图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
【解答】解:由同位角的定义可知,
选项A、选项B、选项C中的∠1与∠2都不是同位角;
选项D中的∠1与∠2是直线AB、BC被直线AD所截所得到的同位角;
故选:D.
5.(3分)把方程=1﹣去分母后,正确的结果是( )
A.2x﹣1=1﹣(3﹣x) B.2(2x﹣1)=1﹣(3﹣x)
C.2(2x﹣1)=8﹣(3﹣x) D.2(2x﹣1)=8﹣3﹣x
【解答】解:方程去分母得:2(2x﹣1)=8﹣3+x,
故选:C.
6.(3分)某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母正好配套,设有x名工人生产螺钉,其他工人生产螺母,则根据题意可列方程为( )
A.2000x=1200(22﹣x) B.2×1200x=2000(22﹣x)
C.2×2000x=1200(22﹣x) D.1200x=2000(22﹣x)
【解答】解:∵有x名工人生产螺钉,
∴有(22﹣x)名工人生产螺母.
∵每天生产螺母的总数是生产螺钉总数的2倍,
∴2×1200x=2000(22﹣x).
故选:B.
7.(3分)有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.|a|>|b| B.ab>0 C.a+b>0 D.|a﹣b|>1
【解答】解:由数轴可得:﹣2<b<﹣1,0<a<1,
则|a|<|b|,故选项A错误;
ab<0,故选项B错误;
a+b<0,故选项C错误;
|a﹣b|>1,正确.
故选:D.
8.(3分)下列说法中错误的有( )个.
①多项式3x2 2x+1的一次项系数是2;
②单项式的系数是﹣2;
③单项式和多项式统称为整式;
④若x2my3 与2x4yn是同类项,那么m﹣n=﹣1.
A.1个 B.2个 C.3个 D.4个
【解答】解:①3x2 2x+1=6x3+1的一次项系数是0;故不符合题意;
②单项式的系数是﹣;故不符合题意;
③单项式和多项式统称为整式;故符合题意;
④∵x2my3 与2x4yn是同类项,
∴2m=4,n=3,
解得m=2,n=3,
∴m﹣n=﹣1,故符合题意;
故选:B.
二、填空题(每小题3分,共计24分)
9.(3分)新疆的总面积约为1660000平方公里,是中国面积最大的省区,约占我国国土面积的六分之一,1660000用科学记数法可表示为 1.66×106 .
【解答】解:1660000=1.66×106,
故答案为:1.66×106.
10.(3分)计算:22°17′×5= 111°25′ .
【解答】解:22°17′×5=110°85′=111°25′,
故答案为:111°25′.
11.(3分)用四舍五入法把0.0568精确到千分位为 0.057 .
【解答】解:用四舍五入法把0.0568精确到千分位为0.057.
故答案为:0.057.
12.(3分)若∠1的对顶角是∠2,∠2的补角是∠3,∠3=54°,则∠1= 126° .
【解答】解:∵∠1的对顶角是∠2,
∴∠1=∠2,
∵∠2的补角是∠3,
∴∠2+∠3=180°,
∵∠3=54°,
∴∠2=126°,
∴∠1=126°,
故答案为:126°.
13.(3分)若与互为相反数,则a的值是 .
【解答】解:∵+1与互为相反数,
∴+1+=0,
去分母得,a+3+2a+1=0,
移项得,a+2a=﹣3﹣1,
合并同类项得,3a=﹣4,
系数化为1得,a=﹣.
故答案为:﹣.
14.(3分)某班级原来女生人数是全班人数的,调入4名女生后,女生人数是全班人数的一半,原来全班共有 36 人.
【解答】解:设原来全班共有x人,则原来女生人数x,
由题意可得:x+4=(x+4),
解得:x=36,
答:原来全班共有36人,
故答案为:36.
15.(3分)如图,直线AB和CD相交于O,OA平分∠COE,∠COE:∠BOE=2:5,则∠EOD的度数为 120° .
【解答】解:∵∠COE:∠BOE=2:5,
∴设∠COE=2x,∠BOE=5x,
∵OA平分∠COE,
∴∠AOE=∠AOC=x,
∵∠AOE+∠BOE=180°,
∴x+5x=180°,
∴x=30°,
∴∠BOE=5x=150°,
∵∠BOD=∠AOC=30°,
∴∠EOD=120°,
故答案为:120°.
16.(3分)直线AB上有两点C、D,点C在A、B之间,满足CA=3CB,,若AB=20,则BD= 0或10 .
【解答】解:如图,∵CA=3CB,AB=20,
∴BC=5,AC=15,
又∵CD=CA,
∴CD=5,
当点D在点C左侧时,BD=5+5=10,
当点D在点C右侧时,点B、D重合,BD=0.
三、解答题(其中17-18题各6分,19-23题各8分,24-25题各10分,共计72分)
17.(6分)计算:
(1)﹣52+(﹣7)×(﹣9)﹣16+(﹣2)3;
(2).
【解答】解:(1)﹣52+(﹣7)×(﹣9)﹣16+(﹣2)3
=﹣25+63﹣16﹣8
=14;
(2)
=×(﹣8)﹣×(﹣﹣4)
=×(﹣8)﹣
=﹣12+
=﹣9.
18.(6分)解方程
(1)1﹣3(8﹣x)=﹣2(15﹣2x);
(2)1=﹣x.
【解答】解:(1)1﹣3(8﹣x)=﹣2(15﹣2x),
去括号,得1﹣24+3x=﹣30+4x,
移项,得3x﹣4x=24﹣30﹣1,
合并同类项,得﹣x=﹣7,
解得x=7;
(2)1=﹣x,
去分母,得12﹣4(2x﹣1)=3(x+1)﹣12x,
去括号,得12﹣8x+4=3x+3﹣12x,
移项,得12x﹣3x﹣8x=3﹣4﹣12,
合并同类项,得x=﹣13.
19.(8分)先化简,再求值:,其中.
【解答】解:原式=3x2y﹣4xy+4xy﹣3x2y﹣x2y2
=﹣x2y2,
当x=3,y=﹣时,
原式=﹣32×(﹣)2
=﹣9×
=﹣1.
20.(8分)如图所示,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.请在括号里填上推理依据.
证明:∵∠1+∠2=180°(已知),
∠1+∠4=180°( 邻补角的定义 ),
∴∠2=∠4( 同角的补角相等 ),
∴AB∥EG( 内错角相等两直线平行 ),
∴∠3= ∠5 ,
又∵∠3=∠B(已知),
∴∠ 5 =∠ B ( 等量代换 ),
∴DE∥BC,
∴∠AED=∠C( 两直线平行同位角相等 ).
【解答】证明:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角的定义),
∴∠2=∠4(同角的补角相等),
∴AB∥EG(内错角相等两直线平行),
∴∠3=∠5,
又∵∠3=∠B(已知),
∴∠5=∠B(等量代换),
∴DE∥BC,
∴∠AED=∠C(两直线平行同位角相等).
21.(8分)中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校2000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩/分 颗数 频率
50≤x<60 50 0.05
60≤x<70 20 0.10
70≤x<80 30 6
80≤x<90 a 0.30
90≤x≤100 80 0.40
请根据所给信息,解答下列问题:
(1)a= 60 ,b= 0.15 ;
(2)通过计算补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的2000名学生中成绩“优”等的大约有多少人?
【解答】解:(1)a=200×0.30=60,b=30÷200=0.15,
故答案为:60、0.15;
(2)补全频数分布直方图,如下:
(3)2000×0.40=800(人).
即该校参加这次比赛的2000名学生中成绩“优”等的大约有800人.
22.(8分)已知:点D在线段AB上,点C是线段AD的中点,AB=4.
(1)如图1,点D是线段AB的中点,求线段CD的长度;
(2)如图2,点E是线段BD的中点,求线段CE的长度.
【解答】解:(1)因为AB=4,点D在线段AB上,点D是线段AB的中点,
所以AD=AB=×4=2,
因为点C是线段AD的中点,
所以CD=AD=×2=1.
(2)因为点D在线段AB上,点C是线段AD的中点,点E是线段BD的中点,
所以CD=AD,DE=BD,
所以CE=CD+DE=AD+BD=(AD+BD)=AB,
因为AB=4,
所以CE=2.
23.(8分)某商场分别购进了甲乙两种型号扫地机器人40台与20台,已知甲种型号扫地机器人每台的进价比乙种型号扫地机器人每台的进价便宜10%,甲种型号扫地机器人每台售价1100元,乙种型号扫地机器人每台售价1500元.
(1)“双十一”期间商场促销,乙种型号扫地机器人按售价八折出售,甲种型号扫地机器人按原价销售.某公司一共花了10300元买了甲乙两种型号扫地机器人共9台.问某公司甲、乙两种型号扫地机器人各买了多少台?
(2)在(1)的条件下甲乙两种型号扫地机器人销售一空,甲种型号扫地机器人利润是乙种型号扫地机器人利润的2倍.问甲乙两种型号扫地机器人每台进价各是多少元?
【解答】解:(1)设该公司买了甲种型号的机器人x台,则买了乙种型号的机器人(9﹣x)台,
依题意,得:1100x+1500×0.8(9﹣x)=10300,
解得:x=5,
∴9﹣x=4.
答:该公司买了甲种型号的机器人5台,买了乙种型号的机器人4台;
(2)设乙型号机器人进价为y元,则甲型号机器人的进价为0.9y元,
依题意,得:40×(1100﹣0.9y)=2×20(1500×0.8﹣y),
解得:y=1000,
∴0.9y=900.
答:乙型号机器人进价为1000元,则甲型号机器人的进价为900元.
24.(10分)阅读下列材料,并解决相应问题:
观察下面一列数:1,2,4,8,…我们发现,这一列数从第2项起,每一项与它前一项的比都等于2.一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比.
(1)如果一个等比数列的第2项是12,第3项是18,则这个等比数列的第1项是 8 ,第4项是 27 ;
(2)为了求等比数列1,2,4,8,…的前2024项的和,可以用如下的方法:求此等比数列前2024项的和,即为求1+2+22+23+…+22023的值,可令S=1+2+22+23+…+22023,则2S=2+22+23+24+…22024,因此2S﹣S=22024﹣1,所以S=1+2+22+23+…+22023=22024﹣1,请仿照以上材料,求出1+6+62+63+…+62023的值,并写明求解过程.
【解答】解:(1)因为等比数列的第2项是12,第3项是18,
所以18÷12=1.5,
即这一个等比数列的公比是1.5.
12÷1.5=8,
故这个等比数列的第1项是8;
18×1.5=27,
故这个等比数列的第4项是27;
故答案为:8,27.
(2)令S=1+6+62+…+62023,
则6S=6+62+63+…+62023+62024,
两式相减得,5S=62024﹣1,
所以.
即1+6+62+63+…+62023的值为.
25.(10分)如图1,O是直线AB上的一点,OC⊥OD,OE平分∠BOC.
(1)若∠AOD=35°,求∠BOE的度数;
(2)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.
①探究∠AOC和∠DOE的度数之间的关系,并说明理由;
②在∠AOC的内部有一条射线OF,∠BOE内部有一条射线OM,且3∠AOD﹣∠AOF+2∠MOE=13∠COE+∠AOF,试确定∠FOM与∠DOE的度数之间的关系,并说明理由.
【解答】解:(1)∵∠AOD=35°,OC⊥OD,
∴∠AOC=∠COD﹣∠AOD=90°﹣35°=55°,
∴∠BOC=180°﹣∠AOC=180°﹣55°=125°.
又∵OE平分∠BOC,
∴∠BOE=∠BOC=×125°=62.5°.
(2)①∵∠BOC=180°﹣∠AOC,OE平分∠BOC,
∴∠COE=∠BOC=(180°﹣∠AOC)=90°﹣∠AOC.
又∵∠DOE=∠COD﹣∠COE=90°﹣∠COE=90°﹣(90°﹣∠AOC),即∠DOE=∠AOC,
∴∠AOC=2∠DOE.
②∠FOM与∠DOE的度数之间的关系:2∠FOM+5∠DOE=540°.
理由如下:由图可知:∠AOD=360°﹣∠COD﹣∠AOC,
∵∠COD=90°,∠AOC=2∠DOE,
∴∠AOD=360°﹣90°﹣2∠DOE=270°﹣2∠DOE,
∵3∠AOD﹣∠AOF+2∠MOE=13∠COE+∠AOF,
∴3(270°﹣2∠DOE)﹣∠AOF+2∠MOE=13∠COE+∠AOF,
∴810°﹣6∠DOE=2∠AOF+13∠COE﹣2∠MOE,
∵OE平分∠BOC.∠AOF=180°﹣∠BOF,∠MOE=∠COM﹣∠COE,
∴∠COE=∠BOC,
∠MOE=∠COM﹣∠BOC,
∴810°﹣6∠DOE=2(180°﹣∠BOF)+13×∠BOC﹣2(∠COM﹣∠BOC),
∴810°﹣6∠DOE=360°﹣2∠BOF+∠BOC﹣2∠COM+∠BOC,
∴450°﹣6∠DOE=﹣2∠BOF+∠BOC﹣2∠COM,
∴450°﹣6∠DOE=﹣2(∠BOF+∠COM)+∠BOC,
∵∠BOC=180°﹣∠AOC=180°﹣2∠DOE,
∠BOF+∠COM=∠BOM+∠MOF+∠COM=∠BOC+∠MOF
∴450°﹣6∠DOE=﹣2(∠BOC+∠MOF)+∠BOC=∠BOC﹣2∠MOF,
∴450°﹣6∠DOE=(180°﹣2∠DOE)﹣2∠MOF,
整理可得:2∠FOM+5∠DOE=540°.
第1页(共1页)
一、选择题(每小题3分,共计24分)
1.(3分)下列方程中,是一元一次方程的是( )
A.x2+2x=3 B.=x C.4x+y=1 D.3x﹣5=3
2.(3分)为了考察某市初中3500名毕业生的数学成绩,从中抽取20本试卷,每本30份,在这个问题中,样本容量是( )
A.3500 B.20 C.30 D.600
3.(3分)下列变形中正确的是( )
A.若x+3=5﹣3x,x+3x=5+3
B.若m=n,则am=an
C.若a=b,则a+c=b﹣c
D.若x=y,则=
4.(3分)下面四个图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
5.(3分)把方程=1﹣去分母后,正确的结果是( )
A.2x﹣1=1﹣(3﹣x) B.2(2x﹣1)=1﹣(3﹣x)
C.2(2x﹣1)=8﹣(3﹣x) D.2(2x﹣1)=8﹣3﹣x
6.(3分)某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母正好配套,设有x名工人生产螺钉,其他工人生产螺母,则根据题意可列方程为( )
A.2000x=1200(22﹣x) B.2×1200x=2000(22﹣x)
C.2×2000x=1200(22﹣x) D.1200x=2000(22﹣x)
7.(3分)有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.|a|>|b| B.ab>0 C.a+b>0 D.|a﹣b|>1
8.(3分)下列说法中错误的有( )个.
①多项式3x2 2x+1的一次项系数是2;
②单项式的系数是﹣2;
③单项式和多项式统称为整式;
④若x2my3 与2x4yn是同类项,那么m﹣n=﹣1.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计24分)
9.(3分)新疆的总面积约为1660000平方公里,是中国面积最大的省区,约占我国国土面积的六分之一,1660000用科学记数法可表示为 .
10.(3分)计算:22°17′×5= .
11.(3分)用四舍五入法把0.0568精确到千分位为 .
12.(3分)若∠1的对顶角是∠2,∠2的补角是∠3,∠3=54°,则∠1= .
13.(3分)若与互为相反数,则a的值是 .
14.(3分)某班级原来女生人数是全班人数的,调入4名女生后,女生人数是全班人数的一半,原来全班共有 人.
15.(3分)如图,直线AB和CD相交于O,OA平分∠COE,∠COE:∠BOE=2:5,则∠EOD的度数为 .
16.(3分)直线AB上有两点C、D,点C在A、B之间,满足CA=3CB,,若AB=20,则BD= .
三、解答题(其中17-18题各6分,19-23题各8分,24-25题各10分,共计72分)
17.(6分)计算:
(1)﹣52+(﹣7)×(﹣9)﹣16+(﹣2)3;
(2).
18.(6分)解方程
(1)1﹣3(8﹣x)=﹣2(15﹣2x);
(2)1=﹣x.
19.(8分)先化简,再求值:,其中.
20.(8分)如图所示,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.请在括号里填上推理依据.
证明:∵∠1+∠2=180°(已知),
∠1+∠4=180°( ),
∴∠2=∠4( ),
∴AB∥EG( ),
∴∠3= ,
又∵∠3=∠B(已知),
∴∠ =∠ ( ),
∴DE∥BC,
∴∠AED=∠C( ).
21.(8分)中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校2000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩/分 颗数 频率
50≤x<60 50 0.05
60≤x<70 20 0.10
70≤x<80 30 6
80≤x<90 a 0.30
90≤x≤100 80 0.40
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)通过计算补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的2000名学生中成绩“优”等的大约有多少人?
22.(8分)已知:点D在线段AB上,点C是线段AD的中点,AB=4.
(1)如图1,点D是线段AB的中点,求线段CD的长度;
(2)如图2,点E是线段BD的中点,求线段CE的长度.
23.(8分)某商场分别购进了甲乙两种型号扫地机器人40台与20台,已知甲种型号扫地机器人每台的进价比乙种型号扫地机器人每台的进价便宜10%,甲种型号扫地机器人每台售价1100元,乙种型号扫地机器人每台售价1500元.
(1)“双十一”期间商场促销,乙种型号扫地机器人按售价八折出售,甲种型号扫地机器人按原价销售.某公司一共花了10300元买了甲乙两种型号扫地机器人共9台.问某公司甲、乙两种型号扫地机器人各买了多少台?
(2)在(1)的条件下甲乙两种型号扫地机器人销售一空,甲种型号扫地机器人利润是乙种型号扫地机器人利润的2倍.问甲乙两种型号扫地机器人每台进价各是多少元?
24.(10分)阅读下列材料,并解决相应问题:
观察下面一列数:1,2,4,8,…我们发现,这一列数从第2项起,每一项与它前一项的比都等于2.一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比.
(1)如果一个等比数列的第2项是12,第3项是18,则这个等比数列的第1项是 ,第4项是 ;
(2)为了求等比数列1,2,4,8,…的前2024项的和,可以用如下的方法:求此等比数列前2024项的和,即为求1+2+22+23+…+22023的值,可令S=1+2+22+23+…+22023,则2S=2+22+23+24+…22024,因此2S﹣S=22024﹣1,所以S=1+2+22+23+…+22023=22024﹣1,请仿照以上材料,求出1+6+62+63+…+62023的值,并写明求解过程.
25.(10分)如图1,O是直线AB上的一点,OC⊥OD,OE平分∠BOC.
(1)若∠AOD=35°,求∠BOE的度数;
(2)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.
①探究∠AOC和∠DOE的度数之间的关系,并说明理由;
②在∠AOC的内部有一条射线OF,∠BOE内部有一条射线OM,且3∠AOD﹣∠AOF+2∠MOE=13∠COE+∠AOF,试确定∠FOM与∠DOE的度数之间的关系,并说明理由.
2023-2024学年黑龙江省哈尔滨市南岗区松雷中学七年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计24分)
1.(3分)下列方程中,是一元一次方程的是( )
A.x2+2x=3 B.=x C.4x+y=1 D.3x﹣5=3
【解答】解:A、含有未知数项的最高次数是2,它不是一元一次方程,故本选项不符合题意;
B、它不是整式方程,不是一元一次方程,故本选项不符合题意;
C、含有2个未知数,不是一元一次方程,故本选项不符合题意;
D、符合一元一次方程的定义,故本选项符合题意.
故选:D.
2.(3分)为了考察某市初中3500名毕业生的数学成绩,从中抽取20本试卷,每本30份,在这个问题中,样本容量是( )
A.3500 B.20 C.30 D.600
【解答】解:为了考察某市初中3500名毕业生的数学成绩,从中抽取20本试卷,每本30份,在这个问题中,样本容量是30×20=600,
故选:D.
3.(3分)下列变形中正确的是( )
A.若x+3=5﹣3x,x+3x=5+3
B.若m=n,则am=an
C.若a=b,则a+c=b﹣c
D.若x=y,则=
【解答】解:A.∵若x+3=5﹣3x,则x+3x=5﹣3,故A选项不正确;
B.若m=n,则am=an,故B选项正确;
C.若a=b,则a+c=b+c,故C选项不正确;
D.若x=y,则=(m≠﹣1),故D选项不正确.
故选:B.
4.(3分)下面四个图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
【解答】解:由同位角的定义可知,
选项A、选项B、选项C中的∠1与∠2都不是同位角;
选项D中的∠1与∠2是直线AB、BC被直线AD所截所得到的同位角;
故选:D.
5.(3分)把方程=1﹣去分母后,正确的结果是( )
A.2x﹣1=1﹣(3﹣x) B.2(2x﹣1)=1﹣(3﹣x)
C.2(2x﹣1)=8﹣(3﹣x) D.2(2x﹣1)=8﹣3﹣x
【解答】解:方程去分母得:2(2x﹣1)=8﹣3+x,
故选:C.
6.(3分)某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母正好配套,设有x名工人生产螺钉,其他工人生产螺母,则根据题意可列方程为( )
A.2000x=1200(22﹣x) B.2×1200x=2000(22﹣x)
C.2×2000x=1200(22﹣x) D.1200x=2000(22﹣x)
【解答】解:∵有x名工人生产螺钉,
∴有(22﹣x)名工人生产螺母.
∵每天生产螺母的总数是生产螺钉总数的2倍,
∴2×1200x=2000(22﹣x).
故选:B.
7.(3分)有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.|a|>|b| B.ab>0 C.a+b>0 D.|a﹣b|>1
【解答】解:由数轴可得:﹣2<b<﹣1,0<a<1,
则|a|<|b|,故选项A错误;
ab<0,故选项B错误;
a+b<0,故选项C错误;
|a﹣b|>1,正确.
故选:D.
8.(3分)下列说法中错误的有( )个.
①多项式3x2 2x+1的一次项系数是2;
②单项式的系数是﹣2;
③单项式和多项式统称为整式;
④若x2my3 与2x4yn是同类项,那么m﹣n=﹣1.
A.1个 B.2个 C.3个 D.4个
【解答】解:①3x2 2x+1=6x3+1的一次项系数是0;故不符合题意;
②单项式的系数是﹣;故不符合题意;
③单项式和多项式统称为整式;故符合题意;
④∵x2my3 与2x4yn是同类项,
∴2m=4,n=3,
解得m=2,n=3,
∴m﹣n=﹣1,故符合题意;
故选:B.
二、填空题(每小题3分,共计24分)
9.(3分)新疆的总面积约为1660000平方公里,是中国面积最大的省区,约占我国国土面积的六分之一,1660000用科学记数法可表示为 1.66×106 .
【解答】解:1660000=1.66×106,
故答案为:1.66×106.
10.(3分)计算:22°17′×5= 111°25′ .
【解答】解:22°17′×5=110°85′=111°25′,
故答案为:111°25′.
11.(3分)用四舍五入法把0.0568精确到千分位为 0.057 .
【解答】解:用四舍五入法把0.0568精确到千分位为0.057.
故答案为:0.057.
12.(3分)若∠1的对顶角是∠2,∠2的补角是∠3,∠3=54°,则∠1= 126° .
【解答】解:∵∠1的对顶角是∠2,
∴∠1=∠2,
∵∠2的补角是∠3,
∴∠2+∠3=180°,
∵∠3=54°,
∴∠2=126°,
∴∠1=126°,
故答案为:126°.
13.(3分)若与互为相反数,则a的值是 .
【解答】解:∵+1与互为相反数,
∴+1+=0,
去分母得,a+3+2a+1=0,
移项得,a+2a=﹣3﹣1,
合并同类项得,3a=﹣4,
系数化为1得,a=﹣.
故答案为:﹣.
14.(3分)某班级原来女生人数是全班人数的,调入4名女生后,女生人数是全班人数的一半,原来全班共有 36 人.
【解答】解:设原来全班共有x人,则原来女生人数x,
由题意可得:x+4=(x+4),
解得:x=36,
答:原来全班共有36人,
故答案为:36.
15.(3分)如图,直线AB和CD相交于O,OA平分∠COE,∠COE:∠BOE=2:5,则∠EOD的度数为 120° .
【解答】解:∵∠COE:∠BOE=2:5,
∴设∠COE=2x,∠BOE=5x,
∵OA平分∠COE,
∴∠AOE=∠AOC=x,
∵∠AOE+∠BOE=180°,
∴x+5x=180°,
∴x=30°,
∴∠BOE=5x=150°,
∵∠BOD=∠AOC=30°,
∴∠EOD=120°,
故答案为:120°.
16.(3分)直线AB上有两点C、D,点C在A、B之间,满足CA=3CB,,若AB=20,则BD= 0或10 .
【解答】解:如图,∵CA=3CB,AB=20,
∴BC=5,AC=15,
又∵CD=CA,
∴CD=5,
当点D在点C左侧时,BD=5+5=10,
当点D在点C右侧时,点B、D重合,BD=0.
三、解答题(其中17-18题各6分,19-23题各8分,24-25题各10分,共计72分)
17.(6分)计算:
(1)﹣52+(﹣7)×(﹣9)﹣16+(﹣2)3;
(2).
【解答】解:(1)﹣52+(﹣7)×(﹣9)﹣16+(﹣2)3
=﹣25+63﹣16﹣8
=14;
(2)
=×(﹣8)﹣×(﹣﹣4)
=×(﹣8)﹣
=﹣12+
=﹣9.
18.(6分)解方程
(1)1﹣3(8﹣x)=﹣2(15﹣2x);
(2)1=﹣x.
【解答】解:(1)1﹣3(8﹣x)=﹣2(15﹣2x),
去括号,得1﹣24+3x=﹣30+4x,
移项,得3x﹣4x=24﹣30﹣1,
合并同类项,得﹣x=﹣7,
解得x=7;
(2)1=﹣x,
去分母,得12﹣4(2x﹣1)=3(x+1)﹣12x,
去括号,得12﹣8x+4=3x+3﹣12x,
移项,得12x﹣3x﹣8x=3﹣4﹣12,
合并同类项,得x=﹣13.
19.(8分)先化简,再求值:,其中.
【解答】解:原式=3x2y﹣4xy+4xy﹣3x2y﹣x2y2
=﹣x2y2,
当x=3,y=﹣时,
原式=﹣32×(﹣)2
=﹣9×
=﹣1.
20.(8分)如图所示,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.请在括号里填上推理依据.
证明:∵∠1+∠2=180°(已知),
∠1+∠4=180°( 邻补角的定义 ),
∴∠2=∠4( 同角的补角相等 ),
∴AB∥EG( 内错角相等两直线平行 ),
∴∠3= ∠5 ,
又∵∠3=∠B(已知),
∴∠ 5 =∠ B ( 等量代换 ),
∴DE∥BC,
∴∠AED=∠C( 两直线平行同位角相等 ).
【解答】证明:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角的定义),
∴∠2=∠4(同角的补角相等),
∴AB∥EG(内错角相等两直线平行),
∴∠3=∠5,
又∵∠3=∠B(已知),
∴∠5=∠B(等量代换),
∴DE∥BC,
∴∠AED=∠C(两直线平行同位角相等).
21.(8分)中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校2000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩/分 颗数 频率
50≤x<60 50 0.05
60≤x<70 20 0.10
70≤x<80 30 6
80≤x<90 a 0.30
90≤x≤100 80 0.40
请根据所给信息,解答下列问题:
(1)a= 60 ,b= 0.15 ;
(2)通过计算补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的2000名学生中成绩“优”等的大约有多少人?
【解答】解:(1)a=200×0.30=60,b=30÷200=0.15,
故答案为:60、0.15;
(2)补全频数分布直方图,如下:
(3)2000×0.40=800(人).
即该校参加这次比赛的2000名学生中成绩“优”等的大约有800人.
22.(8分)已知:点D在线段AB上,点C是线段AD的中点,AB=4.
(1)如图1,点D是线段AB的中点,求线段CD的长度;
(2)如图2,点E是线段BD的中点,求线段CE的长度.
【解答】解:(1)因为AB=4,点D在线段AB上,点D是线段AB的中点,
所以AD=AB=×4=2,
因为点C是线段AD的中点,
所以CD=AD=×2=1.
(2)因为点D在线段AB上,点C是线段AD的中点,点E是线段BD的中点,
所以CD=AD,DE=BD,
所以CE=CD+DE=AD+BD=(AD+BD)=AB,
因为AB=4,
所以CE=2.
23.(8分)某商场分别购进了甲乙两种型号扫地机器人40台与20台,已知甲种型号扫地机器人每台的进价比乙种型号扫地机器人每台的进价便宜10%,甲种型号扫地机器人每台售价1100元,乙种型号扫地机器人每台售价1500元.
(1)“双十一”期间商场促销,乙种型号扫地机器人按售价八折出售,甲种型号扫地机器人按原价销售.某公司一共花了10300元买了甲乙两种型号扫地机器人共9台.问某公司甲、乙两种型号扫地机器人各买了多少台?
(2)在(1)的条件下甲乙两种型号扫地机器人销售一空,甲种型号扫地机器人利润是乙种型号扫地机器人利润的2倍.问甲乙两种型号扫地机器人每台进价各是多少元?
【解答】解:(1)设该公司买了甲种型号的机器人x台,则买了乙种型号的机器人(9﹣x)台,
依题意,得:1100x+1500×0.8(9﹣x)=10300,
解得:x=5,
∴9﹣x=4.
答:该公司买了甲种型号的机器人5台,买了乙种型号的机器人4台;
(2)设乙型号机器人进价为y元,则甲型号机器人的进价为0.9y元,
依题意,得:40×(1100﹣0.9y)=2×20(1500×0.8﹣y),
解得:y=1000,
∴0.9y=900.
答:乙型号机器人进价为1000元,则甲型号机器人的进价为900元.
24.(10分)阅读下列材料,并解决相应问题:
观察下面一列数:1,2,4,8,…我们发现,这一列数从第2项起,每一项与它前一项的比都等于2.一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比.
(1)如果一个等比数列的第2项是12,第3项是18,则这个等比数列的第1项是 8 ,第4项是 27 ;
(2)为了求等比数列1,2,4,8,…的前2024项的和,可以用如下的方法:求此等比数列前2024项的和,即为求1+2+22+23+…+22023的值,可令S=1+2+22+23+…+22023,则2S=2+22+23+24+…22024,因此2S﹣S=22024﹣1,所以S=1+2+22+23+…+22023=22024﹣1,请仿照以上材料,求出1+6+62+63+…+62023的值,并写明求解过程.
【解答】解:(1)因为等比数列的第2项是12,第3项是18,
所以18÷12=1.5,
即这一个等比数列的公比是1.5.
12÷1.5=8,
故这个等比数列的第1项是8;
18×1.5=27,
故这个等比数列的第4项是27;
故答案为:8,27.
(2)令S=1+6+62+…+62023,
则6S=6+62+63+…+62023+62024,
两式相减得,5S=62024﹣1,
所以.
即1+6+62+63+…+62023的值为.
25.(10分)如图1,O是直线AB上的一点,OC⊥OD,OE平分∠BOC.
(1)若∠AOD=35°,求∠BOE的度数;
(2)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.
①探究∠AOC和∠DOE的度数之间的关系,并说明理由;
②在∠AOC的内部有一条射线OF,∠BOE内部有一条射线OM,且3∠AOD﹣∠AOF+2∠MOE=13∠COE+∠AOF,试确定∠FOM与∠DOE的度数之间的关系,并说明理由.
【解答】解:(1)∵∠AOD=35°,OC⊥OD,
∴∠AOC=∠COD﹣∠AOD=90°﹣35°=55°,
∴∠BOC=180°﹣∠AOC=180°﹣55°=125°.
又∵OE平分∠BOC,
∴∠BOE=∠BOC=×125°=62.5°.
(2)①∵∠BOC=180°﹣∠AOC,OE平分∠BOC,
∴∠COE=∠BOC=(180°﹣∠AOC)=90°﹣∠AOC.
又∵∠DOE=∠COD﹣∠COE=90°﹣∠COE=90°﹣(90°﹣∠AOC),即∠DOE=∠AOC,
∴∠AOC=2∠DOE.
②∠FOM与∠DOE的度数之间的关系:2∠FOM+5∠DOE=540°.
理由如下:由图可知:∠AOD=360°﹣∠COD﹣∠AOC,
∵∠COD=90°,∠AOC=2∠DOE,
∴∠AOD=360°﹣90°﹣2∠DOE=270°﹣2∠DOE,
∵3∠AOD﹣∠AOF+2∠MOE=13∠COE+∠AOF,
∴3(270°﹣2∠DOE)﹣∠AOF+2∠MOE=13∠COE+∠AOF,
∴810°﹣6∠DOE=2∠AOF+13∠COE﹣2∠MOE,
∵OE平分∠BOC.∠AOF=180°﹣∠BOF,∠MOE=∠COM﹣∠COE,
∴∠COE=∠BOC,
∠MOE=∠COM﹣∠BOC,
∴810°﹣6∠DOE=2(180°﹣∠BOF)+13×∠BOC﹣2(∠COM﹣∠BOC),
∴810°﹣6∠DOE=360°﹣2∠BOF+∠BOC﹣2∠COM+∠BOC,
∴450°﹣6∠DOE=﹣2∠BOF+∠BOC﹣2∠COM,
∴450°﹣6∠DOE=﹣2(∠BOF+∠COM)+∠BOC,
∵∠BOC=180°﹣∠AOC=180°﹣2∠DOE,
∠BOF+∠COM=∠BOM+∠MOF+∠COM=∠BOC+∠MOF
∴450°﹣6∠DOE=﹣2(∠BOC+∠MOF)+∠BOC=∠BOC﹣2∠MOF,
∴450°﹣6∠DOE=(180°﹣2∠DOE)﹣2∠MOF,
整理可得:2∠FOM+5∠DOE=540°.
第1页(共1页)
同课章节目录
